2021-2022学年人教 版(五四制)八年级上册数学期末练习试卷(word版含解析)
文档属性
| 名称 | 2021-2022学年人教 版(五四制)八年级上册数学期末练习试卷(word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 162.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-16 00:00:00 | ||
图片预览




文档简介
2021-2022学年人教五四新版八年级上学期数学期末练习试卷一.选择题(共10小题,满分30分,每小题3分)
1.下列说法错误的是( )
A.有两边相等的三角形是等腰三角形
B.直角三角形不可能是等腰三角形
C.有两个角为60°的三角形是等边三角形
D.有一个角为60°的等腰三角形是等边三角形
2.在平面直角坐标系中,点(3,2)关于x轴对称的点的坐标为( )
A.(3,﹣2) B.(﹣2,3) C.(2,﹣3) D.(﹣3,2)
3.下列计算正确的是( )
A.x2+2x=3x3 B.(﹣2x3)2=4x5
C.(x+2)(x﹣3)=x2﹣x﹣6 D.(x+y)2=x2+y2
4.如果把分式中的x和y都扩大为原来的2倍,那么分式的值( )
A.扩大为原来的4倍 B.扩大为原来的2倍
C.不变 D.缩小为原来的
5.下列四个图形中,其中不是轴对称图形的是( )
A. B. C. D.
6.三边都不相等的三角形有两边长分别为3和5,第三边长是奇数,则其周长为( )
A.15 B.13 C.11 D.15或13或11
7.要使如图所示的五边形木架不变形,至少要再钉上几根木条( )
A.1根 B.2根 C.3根 D.4根
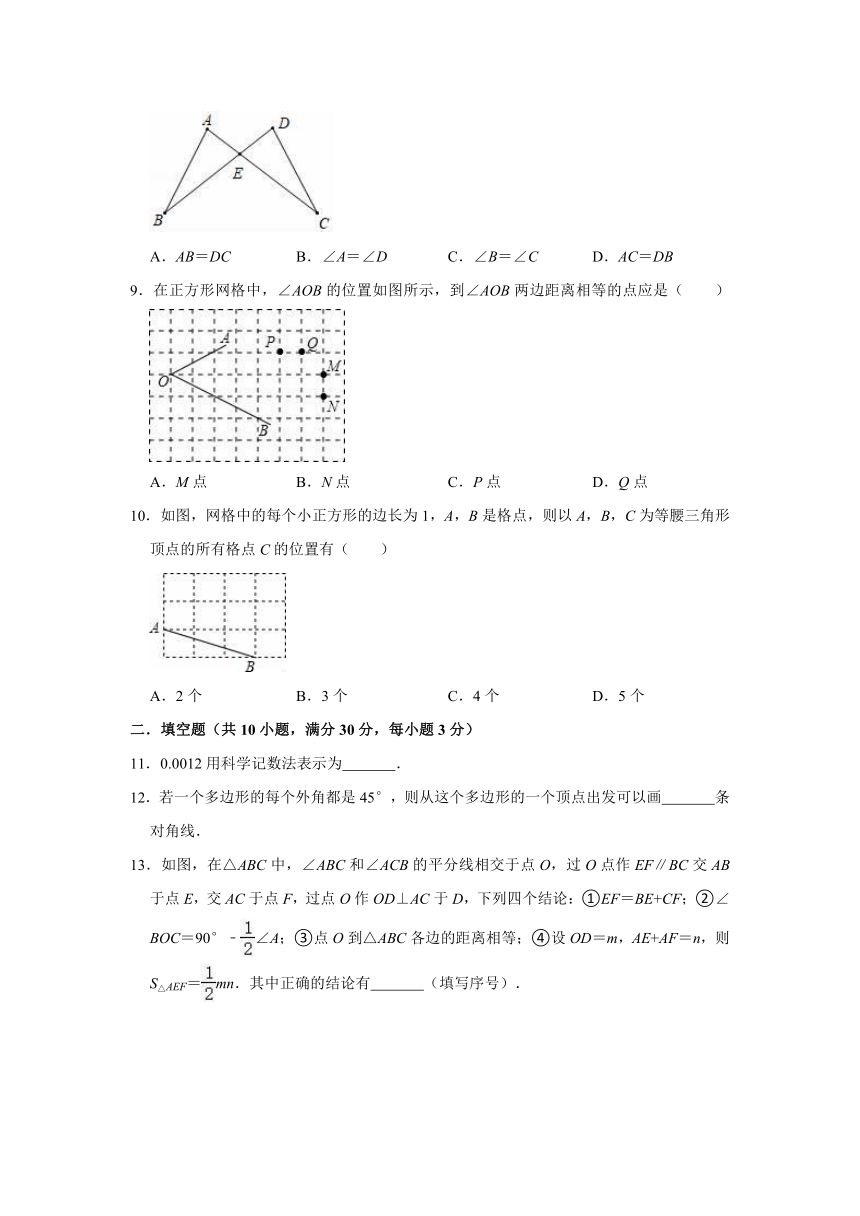
8.如图,AC与DB相交于E,且AE=DE,如果添加一个条件还不能判定△ABE≌△DCE,则添加的这个条件是( )
A.AB=DC B.∠A=∠D C.∠B=∠C D.AC=DB
9.在正方形网格中,∠AOB的位置如图所示,到∠AOB两边距离相等的点应是( )
A.M点 B.N点 C.P点 D.Q点
10.如图,网格中的每个小正方形的边长为1,A,B是格点,则以A,B,C为等腰三角形顶点的所有格点C的位置有( )
A.2个 B.3个 C.4个 D.5个
二.填空题(共10小题,满分30分,每小题3分)
11.0.0012用科学记数法表示为 .
12.若一个多边形的每个外角都是45°,则从这个多边形的一个顶点出发可以画 条对角线.
13.如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过O点作EF∥BC交AB于点E,交AC于点F,过点O作OD⊥AC于D,下列四个结论:①EF=BE+CF;②∠BOC=90°﹣∠A;③点O到△ABC各边的距离相等;④设OD=m,AE+AF=n,则S△AEF=mn.其中正确的结论有 (填写序号).
14.如果x2﹣2(m+1)x+m2+5是一个完全平方式,则m= .
15.解方程:=﹣1,则x= .
16.分解因式:m2n﹣4mn﹣4n= .
17.若多项式A除以2x2﹣3,得到的商式为3x﹣4,余式为5x+2,则A= .
18.△ABC的三边长分别为1,3,x,且x为整数,则x的值是 .
19.已知△ABC中有一个内角是30°,AB=AC,AB边上的中垂线交直线BC于点D,连结AD,则∠DAC= .
20.若a+=3,则a﹣= .
三.解答题(共7小题,满分60分)
21.(7分)计算:
(1)(2x)3(﹣5xy2);
(2)4(x+1)2﹣(2x+5)(2x﹣5).
22.(7分)已知,如图,在平面直角坐标系中,A(﹣1,4),B(﹣2,1),C(﹣4,1).
(1)请作出△ABC关于y轴的对称图形△A1B1C1;
(2)直接写出点A1,B1,C1的坐标,A1 B1 C1 .
(3)P为y轴上一点,在图中画出使△PAB的周长最小时的点P,并直接写出此时点P的坐标.
23.(8分)先化简,再求值:(1﹣)÷,其中a=(2021﹣π)0.
24.(8分)已知:如图,AB=AC,D是AB上一点,DE⊥BC于点E,ED的延长线交CA的延长线于点F.求证:△ADF是等腰三角形.
25.(10分)某中学为了创设“书香校园”,准备购买A、B两种书架,用于放置图书.在购买时发现,A种书架的单价比B种书架的单价多20元,用720元购买A种书架的个数与用600元购买B种书架的个数相同.
(1)求A、B两种书架的单价各是多少元?
(2)学校准备购买A、B两种书架共15个,且购买的总费用不超过1600元,求最多可以购买多少个A种书架?
26.(10分)(1)思考探究:如图,△ABC的内角∠ABC的平分线与外角∠ACD的平分线相交于P点,已知∠ABC=70°,∠ACD=100°.求∠A和∠P的度数;
(2)类比探究:如图,△ABC的内角∠ABC的平分线与外角∠ACD的平分线相交于P点,已知∠P=n°.求∠A的度数(用含n的式子表示);
(3)拓展迁移:已知,在四边形ABCD中,四边形ABCD的内角∠ABC与外角∠DCE的平分线所在直线相交于点P,∠P=n°,请画出图形;并探究出∠A+∠D的度数(用含n的式子表示).
27.(10分)如图,在等边△ABC的AC,BC上各取一点D,E,使AD=CE,AE,BD相交于点M,过点B作直线AE的垂线BH,垂足为H.
(1)求证:△ACE≌△BAD;
(2)若BE=2EC=4.
①求△ABC的面积;
②求MH的长.
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.解:A.有两边相等的三角形是等腰三角形,该说法正确,故本选项不合题意;
B.直角三角形可能是等腰三角形,原说法错误,故本选项符合题意;
C.有两个角为60°的三角形是等边三角形,该说法正确,故本选项不合题意;
D.有一个角为60°的等腰三角形是等边三角形,该说法正确,故本选项不合题意;
故选:B.
2.解:点(3,2)关于x轴对称的点的坐标为(3,﹣2).
故选:A.
3.解:A.x2和2x不是同类项,不能合并,故本选项不符合题意;
B.(﹣2x3)2=4x6,故本选项不符合题意;
C.(x+2)(x﹣3)=x2﹣x﹣6,故本选项符合题意;
D.(x+y)2=x2+2xy+y2,故本选项不符合题意;
故选:C.
4.解:∵x,y都扩大为原来2倍,
∴分子xy扩大4倍,分母x+y扩大2倍,
∴分式扩大为原来的2倍.
故选:B.
5.解:选项A、C、D能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形,
选项B不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形,
故选:B.
6.解:设第三边长为x.
根据三角形的三边关系,则有5﹣3<x<5+3,
即2<x<8,
因为三边都不相等,第三边长是奇数,
所以x=7,
所以周长=3+5+7=15.
故选:A.
7.解:过五边形的一个顶点作对角线,有5﹣3=2条对角线,所以至少要钉上2根木条.
故选:B.
8.解:根据题意,已知AE=DE,∠AEB=∠DEC,
∴只需添加对顶角的邻边,即EB=EC(由AC=DB可以得到),
或任意一组对应角,即∠A=∠D,∠B=∠C;
所以,选项A符合题意.
故选:A.
9.解:从图上可以看出点M在∠AOB的平分线上,其它三点不在∠AOB的平分线上.
所以点M到∠AOB两边的距离相等.故选A.
10.解:由勾股定理得:AB==,
分三种情况:如图所示:
①当A为顶角顶点时,符合△ABC为等腰三角形的C点有1个;
②当B为顶角顶点时,符合△ABC为等腰三角形的C点有2个;
③当C为顶角顶点时,符合△ABC为等腰三角形的C点有1个;
综上所述:以A,B,C为等腰三角形顶点的所有格点C的位置有1+2+1=4(个);
故选:C.
二.填空题(共10小题,满分30分,每小题3分)
11.解:将0.0012用科学记数法表示为1.2×10﹣3,
故答案是:1.2×10﹣3.
12.解:正多边形的边数:360÷45=8,
从这个正多边形的一个顶点出发,共可以作对角线的条数为:8﹣3=5,
故答案为:5.
13.解:在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴∠OBC=∠ABC,∠OCB=∠ACB,∠A+∠ABC+∠ACB=180°,
∴∠OBC+∠OCB=90°﹣∠A,
∴∠BOC=180°﹣(∠OBC+∠OCB)=90°+∠A;故②错误;
在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴∠OBC=∠OBE,∠OCB=∠OCF,
∵EF∥BC,
∴∠OBC=∠EOB,∠OCB=∠FOC,
∴∠EOB=∠OBE,∠FOC=∠OCF,
∴BE=OE,CF=OF,
∴EF=OE+OF=BE+CF,
故①正确;
过点O作OM⊥AB于M,作ON⊥BC于N,连接OA,
在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴ON=OD=OM=m,
∴S△AEF=S△AOE+S△AOF=AE OM+AF OD=OD (AE+AF)=mn;故④正确;
在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴点O到△ABC各边的距离相等,故③正确.
故答案为:①③④.
14.解:∵m2+5=(m+1)2=m2+2m+1,
∴m=2.
15.解:去分母得:3x=2﹣3x﹣3,
解得:x=﹣,
经检验x=﹣是分式方程的解,
故答案为:﹣
16.解:m2n﹣4mn﹣4n=n(m2﹣4m﹣4).
故答案为n(m2﹣4m﹣4).
17.解:∵多项式A除以2x2﹣3,得到的商为3x﹣4,余式为5x+2,
∴A=(2x2﹣3)(3x﹣4)+5x+2=6x3﹣8x2﹣9x+12+5x+2=6x3﹣8x2﹣4x+14.
故答案为:6x3﹣8x2﹣4x+14.
18.解:根据三角形三边关系,
∴三角形的第三边x满足:3﹣1<x<3+1,即2<x<4,
∵x为整数,
∴x=3,
故答案为:3.
19.解:∠B=30°是底角,如图1:
∵AB=AC,∠B=30°,
∴∠C=30°,
∵AB边上的中垂线交直线BC于点D,
∴∠BAD=∠B=30°,
∴∠ADC=30°+30°=60°,
∴∠DAC=180°﹣30°﹣60°=90°;
∠BAC=30°的角是顶角,如图2:
∵AB=AC,∠BAC=30°,
∴∠B=∠ACB=(180°﹣30°)÷2=75°,
∵AB边上的中垂线交直线BC于点D,
∴∠BED=∠AED=90°﹣75°=15°,
∴∠ADC=15°+15°=30°,
∴∠DAC=75°﹣30°=45°.
故∠DAC=90°或45°.
故答案为:90°或45°.
20.解:∵(x+y)2﹣4xy=(x﹣y)2,
∴﹣4=,
∴a﹣=±.
三.解答题(共7小题,满分60分)
21.解:(1)(2x)3(﹣5xy2)
=8x3 (﹣5xy2)
=﹣40x4y2;
(2)4(x+1)2﹣(2x+5)(2x﹣5)
=4(x2+2x+1)﹣(4x2﹣25)
=4x2+8x+4﹣4x2+25
=8x+29.
22.解:(1)如图所示,△A1B1C1即为所求.
(2)由图知,A1(1,4),B1(2,1),C1(4,1),
故答案为:(1,4),(2,1),(4,1);
(3)如图所示,点P即为所求,其坐标为(0,3).
23.解:(1﹣)÷
=
=
=,
当a=(2021﹣π)0=1时,原式==﹣.
24.解:∵AB=AC,
∴∠B=∠C(等边对等角),
∵DE⊥BC于E,
∴∠FEB=∠FEC=90°,
∴∠B+∠EDB=∠C+∠EFC=90°,
∴∠EFC=∠EDB(等角的余角相等),
∵∠EDB=∠ADF(对顶角相等),
∴∠EFC=∠ADF,
∴AD=AF,
∴△ADF是等腰三角形.
25.解:(1)设B种书架单价为 x元,则A种书架单价为(x+20)元,
根据题意,可得.
解得:x=100.
经检验,x=100是原分式方程的解,
∴x+20=120.
答:A种书架单价120元,B种书架单价100元.
(2)设准备购买y个A种书架,则购买B种书架(15﹣y)个,
根据题意有120y+100(15﹣y)≤1600.
解得:y≤5.
答:最多购买5个A种书架.
26.解:(1)∵∠ABC=70°,∠ACD=100°,
∴∠A=100°﹣70°=30°,
∵P点是∠ABC和外角∠ACD的角平分线的交点,
∴∠PCD=∠ACD=50°,∠PBC=∠ABC=35°,
∴∠P=50°﹣35°=15°;
(2)∠A=2n°.
理由:∵∠PCD=∠P+∠PBC,∠ACD=∠A+∠ABC,
∵P点是∠ABC和外角∠ACD的角平分线的交点,
∴∠ACD=2∠PCD,∠ABC=2∠PBC,
∴∠A+∠ABC=2(∠P+∠PBC),
∠A+∠ABC=2∠P+2∠PBC,
∠A+∠ABC=2∠P+∠ABC,
∴∠A=2∠P,
∴∠A=2n°;
(3)(Ⅰ)如图②延长BA交CD的延长线于F.
∵∠F=180°﹣∠FAD﹣∠FDA=180°﹣(180°﹣∠A)﹣(180°﹣∠D)=∠A+∠D﹣180°,
由(2)可知:∠F=2∠P=2n°,
∴∠A+∠D=180°+2n°.
(Ⅱ)如图③,延长AB交DC的延长线于F.
∵∠F=180°﹣∠A﹣∠D,∠P=∠F,
∴∠P=(180°﹣∠A﹣∠D)=90°﹣(∠A+∠D).
∴∠A+∠D=180°﹣2n°
综上所述:∠A+∠D=180°+2n°或180°﹣2n°.
27.证明:(1)∵△ABC是等边三角形,
∴AB=AC,∠BAC=∠C=60°,
在△ACE和△BAD中,
,
∴△ACE≌△BAD(SAS);
(2)①∵BE=2EC=4,
∴EC=2,
∴BC=6,
∴△ABC的面积=×36=9;
②如图,过点A作AF⊥BC于F,
∵AB=AC,AF⊥BC,
∴BF=CF=3,
∴EF=1,AF=BF=3,
∴AE===2,
∵S△ABE=×AE×BH=BE×AF,
∴BH==,
∵△ACE≌△BAD,
∴∠CAE=∠ABD,
∴∠BMH=∠BAE+∠ABD=∠CAE+∠BAE=60°,
∴∠DBH=30°,
∴BH=MH,
∴MH=.
1.下列说法错误的是( )
A.有两边相等的三角形是等腰三角形
B.直角三角形不可能是等腰三角形
C.有两个角为60°的三角形是等边三角形
D.有一个角为60°的等腰三角形是等边三角形
2.在平面直角坐标系中,点(3,2)关于x轴对称的点的坐标为( )
A.(3,﹣2) B.(﹣2,3) C.(2,﹣3) D.(﹣3,2)
3.下列计算正确的是( )
A.x2+2x=3x3 B.(﹣2x3)2=4x5
C.(x+2)(x﹣3)=x2﹣x﹣6 D.(x+y)2=x2+y2
4.如果把分式中的x和y都扩大为原来的2倍,那么分式的值( )
A.扩大为原来的4倍 B.扩大为原来的2倍
C.不变 D.缩小为原来的
5.下列四个图形中,其中不是轴对称图形的是( )
A. B. C. D.
6.三边都不相等的三角形有两边长分别为3和5,第三边长是奇数,则其周长为( )
A.15 B.13 C.11 D.15或13或11
7.要使如图所示的五边形木架不变形,至少要再钉上几根木条( )
A.1根 B.2根 C.3根 D.4根
8.如图,AC与DB相交于E,且AE=DE,如果添加一个条件还不能判定△ABE≌△DCE,则添加的这个条件是( )
A.AB=DC B.∠A=∠D C.∠B=∠C D.AC=DB
9.在正方形网格中,∠AOB的位置如图所示,到∠AOB两边距离相等的点应是( )
A.M点 B.N点 C.P点 D.Q点
10.如图,网格中的每个小正方形的边长为1,A,B是格点,则以A,B,C为等腰三角形顶点的所有格点C的位置有( )
A.2个 B.3个 C.4个 D.5个
二.填空题(共10小题,满分30分,每小题3分)
11.0.0012用科学记数法表示为 .
12.若一个多边形的每个外角都是45°,则从这个多边形的一个顶点出发可以画 条对角线.
13.如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过O点作EF∥BC交AB于点E,交AC于点F,过点O作OD⊥AC于D,下列四个结论:①EF=BE+CF;②∠BOC=90°﹣∠A;③点O到△ABC各边的距离相等;④设OD=m,AE+AF=n,则S△AEF=mn.其中正确的结论有 (填写序号).
14.如果x2﹣2(m+1)x+m2+5是一个完全平方式,则m= .
15.解方程:=﹣1,则x= .
16.分解因式:m2n﹣4mn﹣4n= .
17.若多项式A除以2x2﹣3,得到的商式为3x﹣4,余式为5x+2,则A= .
18.△ABC的三边长分别为1,3,x,且x为整数,则x的值是 .
19.已知△ABC中有一个内角是30°,AB=AC,AB边上的中垂线交直线BC于点D,连结AD,则∠DAC= .
20.若a+=3,则a﹣= .
三.解答题(共7小题,满分60分)
21.(7分)计算:
(1)(2x)3(﹣5xy2);
(2)4(x+1)2﹣(2x+5)(2x﹣5).
22.(7分)已知,如图,在平面直角坐标系中,A(﹣1,4),B(﹣2,1),C(﹣4,1).
(1)请作出△ABC关于y轴的对称图形△A1B1C1;
(2)直接写出点A1,B1,C1的坐标,A1 B1 C1 .
(3)P为y轴上一点,在图中画出使△PAB的周长最小时的点P,并直接写出此时点P的坐标.
23.(8分)先化简,再求值:(1﹣)÷,其中a=(2021﹣π)0.
24.(8分)已知:如图,AB=AC,D是AB上一点,DE⊥BC于点E,ED的延长线交CA的延长线于点F.求证:△ADF是等腰三角形.
25.(10分)某中学为了创设“书香校园”,准备购买A、B两种书架,用于放置图书.在购买时发现,A种书架的单价比B种书架的单价多20元,用720元购买A种书架的个数与用600元购买B种书架的个数相同.
(1)求A、B两种书架的单价各是多少元?
(2)学校准备购买A、B两种书架共15个,且购买的总费用不超过1600元,求最多可以购买多少个A种书架?
26.(10分)(1)思考探究:如图,△ABC的内角∠ABC的平分线与外角∠ACD的平分线相交于P点,已知∠ABC=70°,∠ACD=100°.求∠A和∠P的度数;
(2)类比探究:如图,△ABC的内角∠ABC的平分线与外角∠ACD的平分线相交于P点,已知∠P=n°.求∠A的度数(用含n的式子表示);
(3)拓展迁移:已知,在四边形ABCD中,四边形ABCD的内角∠ABC与外角∠DCE的平分线所在直线相交于点P,∠P=n°,请画出图形;并探究出∠A+∠D的度数(用含n的式子表示).
27.(10分)如图,在等边△ABC的AC,BC上各取一点D,E,使AD=CE,AE,BD相交于点M,过点B作直线AE的垂线BH,垂足为H.
(1)求证:△ACE≌△BAD;
(2)若BE=2EC=4.
①求△ABC的面积;
②求MH的长.
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.解:A.有两边相等的三角形是等腰三角形,该说法正确,故本选项不合题意;
B.直角三角形可能是等腰三角形,原说法错误,故本选项符合题意;
C.有两个角为60°的三角形是等边三角形,该说法正确,故本选项不合题意;
D.有一个角为60°的等腰三角形是等边三角形,该说法正确,故本选项不合题意;
故选:B.
2.解:点(3,2)关于x轴对称的点的坐标为(3,﹣2).
故选:A.
3.解:A.x2和2x不是同类项,不能合并,故本选项不符合题意;
B.(﹣2x3)2=4x6,故本选项不符合题意;
C.(x+2)(x﹣3)=x2﹣x﹣6,故本选项符合题意;
D.(x+y)2=x2+2xy+y2,故本选项不符合题意;
故选:C.
4.解:∵x,y都扩大为原来2倍,
∴分子xy扩大4倍,分母x+y扩大2倍,
∴分式扩大为原来的2倍.
故选:B.
5.解:选项A、C、D能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形,
选项B不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形,
故选:B.
6.解:设第三边长为x.
根据三角形的三边关系,则有5﹣3<x<5+3,
即2<x<8,
因为三边都不相等,第三边长是奇数,
所以x=7,
所以周长=3+5+7=15.
故选:A.
7.解:过五边形的一个顶点作对角线,有5﹣3=2条对角线,所以至少要钉上2根木条.
故选:B.
8.解:根据题意,已知AE=DE,∠AEB=∠DEC,
∴只需添加对顶角的邻边,即EB=EC(由AC=DB可以得到),
或任意一组对应角,即∠A=∠D,∠B=∠C;
所以,选项A符合题意.
故选:A.
9.解:从图上可以看出点M在∠AOB的平分线上,其它三点不在∠AOB的平分线上.
所以点M到∠AOB两边的距离相等.故选A.
10.解:由勾股定理得:AB==,
分三种情况:如图所示:
①当A为顶角顶点时,符合△ABC为等腰三角形的C点有1个;
②当B为顶角顶点时,符合△ABC为等腰三角形的C点有2个;
③当C为顶角顶点时,符合△ABC为等腰三角形的C点有1个;
综上所述:以A,B,C为等腰三角形顶点的所有格点C的位置有1+2+1=4(个);
故选:C.
二.填空题(共10小题,满分30分,每小题3分)
11.解:将0.0012用科学记数法表示为1.2×10﹣3,
故答案是:1.2×10﹣3.
12.解:正多边形的边数:360÷45=8,
从这个正多边形的一个顶点出发,共可以作对角线的条数为:8﹣3=5,
故答案为:5.
13.解:在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴∠OBC=∠ABC,∠OCB=∠ACB,∠A+∠ABC+∠ACB=180°,
∴∠OBC+∠OCB=90°﹣∠A,
∴∠BOC=180°﹣(∠OBC+∠OCB)=90°+∠A;故②错误;
在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴∠OBC=∠OBE,∠OCB=∠OCF,
∵EF∥BC,
∴∠OBC=∠EOB,∠OCB=∠FOC,
∴∠EOB=∠OBE,∠FOC=∠OCF,
∴BE=OE,CF=OF,
∴EF=OE+OF=BE+CF,
故①正确;
过点O作OM⊥AB于M,作ON⊥BC于N,连接OA,
在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴ON=OD=OM=m,
∴S△AEF=S△AOE+S△AOF=AE OM+AF OD=OD (AE+AF)=mn;故④正确;
在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴点O到△ABC各边的距离相等,故③正确.
故答案为:①③④.
14.解:∵m2+5=(m+1)2=m2+2m+1,
∴m=2.
15.解:去分母得:3x=2﹣3x﹣3,
解得:x=﹣,
经检验x=﹣是分式方程的解,
故答案为:﹣
16.解:m2n﹣4mn﹣4n=n(m2﹣4m﹣4).
故答案为n(m2﹣4m﹣4).
17.解:∵多项式A除以2x2﹣3,得到的商为3x﹣4,余式为5x+2,
∴A=(2x2﹣3)(3x﹣4)+5x+2=6x3﹣8x2﹣9x+12+5x+2=6x3﹣8x2﹣4x+14.
故答案为:6x3﹣8x2﹣4x+14.
18.解:根据三角形三边关系,
∴三角形的第三边x满足:3﹣1<x<3+1,即2<x<4,
∵x为整数,
∴x=3,
故答案为:3.
19.解:∠B=30°是底角,如图1:
∵AB=AC,∠B=30°,
∴∠C=30°,
∵AB边上的中垂线交直线BC于点D,
∴∠BAD=∠B=30°,
∴∠ADC=30°+30°=60°,
∴∠DAC=180°﹣30°﹣60°=90°;
∠BAC=30°的角是顶角,如图2:
∵AB=AC,∠BAC=30°,
∴∠B=∠ACB=(180°﹣30°)÷2=75°,
∵AB边上的中垂线交直线BC于点D,
∴∠BED=∠AED=90°﹣75°=15°,
∴∠ADC=15°+15°=30°,
∴∠DAC=75°﹣30°=45°.
故∠DAC=90°或45°.
故答案为:90°或45°.
20.解:∵(x+y)2﹣4xy=(x﹣y)2,
∴﹣4=,
∴a﹣=±.
三.解答题(共7小题,满分60分)
21.解:(1)(2x)3(﹣5xy2)
=8x3 (﹣5xy2)
=﹣40x4y2;
(2)4(x+1)2﹣(2x+5)(2x﹣5)
=4(x2+2x+1)﹣(4x2﹣25)
=4x2+8x+4﹣4x2+25
=8x+29.
22.解:(1)如图所示,△A1B1C1即为所求.
(2)由图知,A1(1,4),B1(2,1),C1(4,1),
故答案为:(1,4),(2,1),(4,1);
(3)如图所示,点P即为所求,其坐标为(0,3).
23.解:(1﹣)÷
=
=
=,
当a=(2021﹣π)0=1时,原式==﹣.
24.解:∵AB=AC,
∴∠B=∠C(等边对等角),
∵DE⊥BC于E,
∴∠FEB=∠FEC=90°,
∴∠B+∠EDB=∠C+∠EFC=90°,
∴∠EFC=∠EDB(等角的余角相等),
∵∠EDB=∠ADF(对顶角相等),
∴∠EFC=∠ADF,
∴AD=AF,
∴△ADF是等腰三角形.
25.解:(1)设B种书架单价为 x元,则A种书架单价为(x+20)元,
根据题意,可得.
解得:x=100.
经检验,x=100是原分式方程的解,
∴x+20=120.
答:A种书架单价120元,B种书架单价100元.
(2)设准备购买y个A种书架,则购买B种书架(15﹣y)个,
根据题意有120y+100(15﹣y)≤1600.
解得:y≤5.
答:最多购买5个A种书架.
26.解:(1)∵∠ABC=70°,∠ACD=100°,
∴∠A=100°﹣70°=30°,
∵P点是∠ABC和外角∠ACD的角平分线的交点,
∴∠PCD=∠ACD=50°,∠PBC=∠ABC=35°,
∴∠P=50°﹣35°=15°;
(2)∠A=2n°.
理由:∵∠PCD=∠P+∠PBC,∠ACD=∠A+∠ABC,
∵P点是∠ABC和外角∠ACD的角平分线的交点,
∴∠ACD=2∠PCD,∠ABC=2∠PBC,
∴∠A+∠ABC=2(∠P+∠PBC),
∠A+∠ABC=2∠P+2∠PBC,
∠A+∠ABC=2∠P+∠ABC,
∴∠A=2∠P,
∴∠A=2n°;
(3)(Ⅰ)如图②延长BA交CD的延长线于F.
∵∠F=180°﹣∠FAD﹣∠FDA=180°﹣(180°﹣∠A)﹣(180°﹣∠D)=∠A+∠D﹣180°,
由(2)可知:∠F=2∠P=2n°,
∴∠A+∠D=180°+2n°.
(Ⅱ)如图③,延长AB交DC的延长线于F.
∵∠F=180°﹣∠A﹣∠D,∠P=∠F,
∴∠P=(180°﹣∠A﹣∠D)=90°﹣(∠A+∠D).
∴∠A+∠D=180°﹣2n°
综上所述:∠A+∠D=180°+2n°或180°﹣2n°.
27.证明:(1)∵△ABC是等边三角形,
∴AB=AC,∠BAC=∠C=60°,
在△ACE和△BAD中,
,
∴△ACE≌△BAD(SAS);
(2)①∵BE=2EC=4,
∴EC=2,
∴BC=6,
∴△ABC的面积=×36=9;
②如图,过点A作AF⊥BC于F,
∵AB=AC,AF⊥BC,
∴BF=CF=3,
∴EF=1,AF=BF=3,
∴AE===2,
∵S△ABE=×AE×BH=BE×AF,
∴BH==,
∵△ACE≌△BAD,
∴∠CAE=∠ABD,
∴∠BMH=∠BAE+∠ABD=∠CAE+∠BAE=60°,
∴∠DBH=30°,
∴BH=MH,
∴MH=.
同课章节目录
