2021-2022学年北师大版九年级上册数学第六章反比例函数期末专题复习题(Word版,附答案解析)
文档属性
| 名称 | 2021-2022学年北师大版九年级上册数学第六章反比例函数期末专题复习题(Word版,附答案解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 359.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-16 00:00:00 | ||
图片预览


文档简介
九上数学反比例函数综合复习题
一、单选题
1.下列各点中,在反比例函数 图象上的是( )
A. (-1,8) B. (-2,4) C. (1,7) D. (2,4)
2.如图,已知直线y=mx与双曲线y=的一个交点坐标为(3,4),则它们的另一个交点坐标是( )
A.(﹣3,4) B.(﹣4,﹣3) C.(﹣3,﹣4) D.(4,3)
3.如图是反比例函数y=(k为常数,k≠0)的图象,则一次函数y=kx﹣k的图象大致是( )
A.B.C.D.
4.如图,点A是反比例函数(x>0)图象上任意一点,AB⊥y轴于B,点C是x轴上的动点,则△ABC的面积为( )
A.1 B.2 C.4 D.不能确定
5.已知点A(﹣1,y1)、B(﹣2,y2)、C(3,y3)都在反比例函数y= 的图象上,则y1、y2、y3的关系是( )
A. y2>y1>y3 B. y2>y3>y1 C. y3>y1>y2 D. y3>y2>y1
6.如图,P是双曲线上一点,且图中△POA的面积为5,则此反比例函数的解析式为( )
A.y= B.y=﹣ C.y= D.y=
7.函数y=(k≠0)的图象如图所示,那么函数y=kx﹣k的图象大致是( )
A.B.C.D.
8.若点A(1,y1),B(2,y2),C(﹣2,y3)都在反比例函数y=(k>0)的图象上,则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y2<y3<y1 C.y1<y3<y2 D.y3<y2<y1
9.如图所示,已知 为反比例函数 图象上的两点,动点 在 轴正半轴上运动,当 的值最大时,连结 , 的面积是 ( )
A. B. 1 C. D.
10.如图,直线 与 轴、 轴相交于 , 两点,与 的图象相交于 , 两点,连接 , .下列结论:① ;②不等式 的解集是 或 ;③ ;④ .其中正确的结论是( )
A. ①③ B. ②③④ C. ①③④ D. ②④
二、填空题
11.如果直线y=mx与双曲线y=的一个交点A的坐标为(3,2),则它们的另一个交点B的坐标为 .
12.已知一菱形的面积为12cm2,对角线长分别为xcm和ycm,则y与x的函数关系式为
13.码头工人往一艘轮船上装载货物,装完货物所需时间y(min)与装载速度x(t/min)之间的函数关系如图(双曲线y=的一支).如果以5t/min的速度卸货,那么卸完货物需要时间是 min.
14.如图,P为反比例函数y=图象上一点,过点P分别向x轴,y轴引垂线,垂足分别为M、N,直线y=﹣x+1与PM、PN分别交于点E、F,与x轴、y轴分别交于A、B,则AF BE= .
15.如图,在平面直角坐标系中,O为坐标原点,MN垂直于x轴,以MN为对称轴作△ODE的轴对称图形,对称轴MN与线段DE相交于点F,点D的对应点B恰好落在y=(k≠0,x<0)的双曲线上,点O、E的对应点分别是点C、A.若点A为OE的中点,且S△AEF=1,则k的值为 .
16.如图,A、B两点在反比例函数y=﹣(x<0)的图象上,AB的延长线交x轴于点C,且AB=2BC,则△AOC的面积是 .
三、解答题
17.如图,已知一次函数y1=kx+b与反比例函数y2= 的图象交于 、 两点.分别求出y1和y2的解析式.
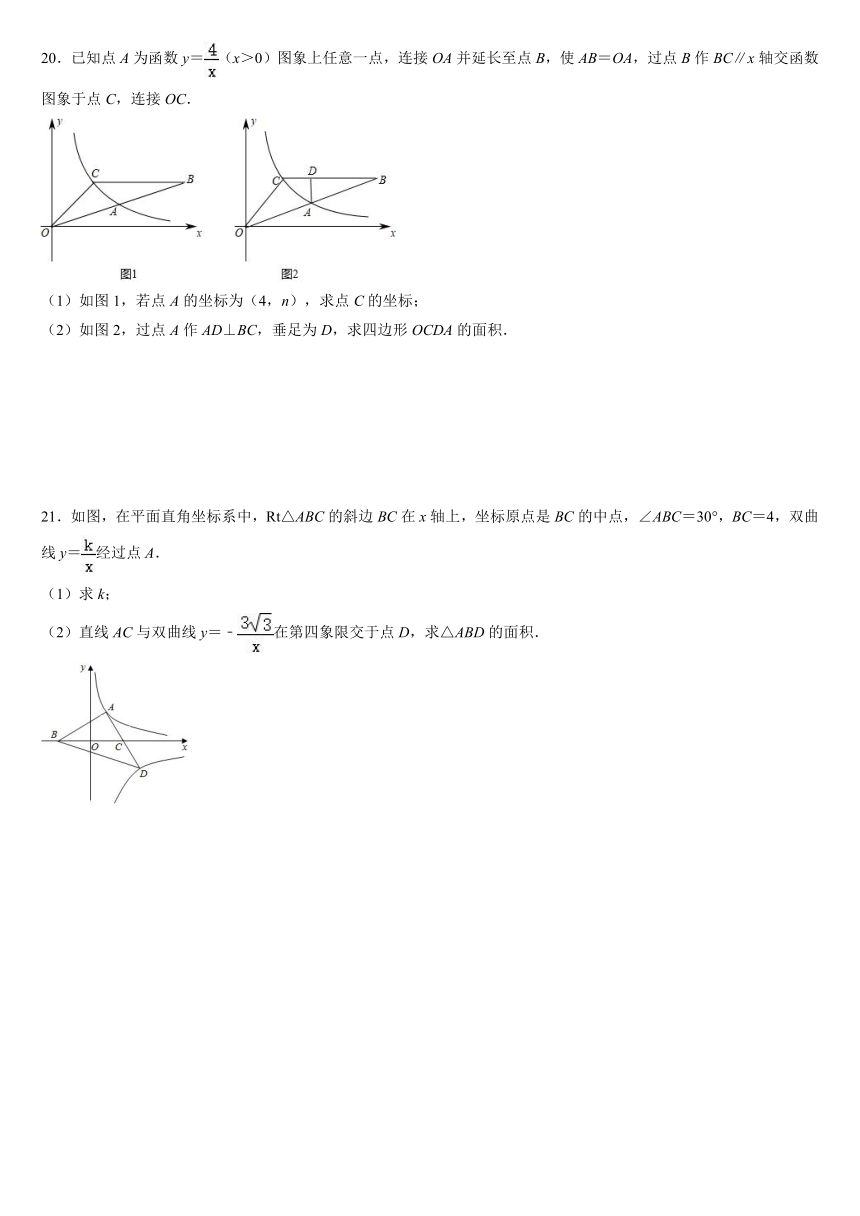
18.如图所示,在平面直角坐标系中,一次函数 与反比例函数 的图像交于第二、四象限 、 两点,过点 作 轴于点 , , ,且点 的坐标为 .
(1)求一次函数与反比例函数的解析式.
(2) 是 轴上一点,且 是等腰三角形,请直接写出所有符合条件的 点坐标.
19.如图,在平面直角坐标系中,矩形OABC的两边OC、OA分别在坐标轴上,且OA=2,OC=4,连接OB.反比例函数y=(x>0)的图象经过线段OB的中点D,并与AB、BC分别交于点E、F.一次函数y=k2x+b的图象经过E、F两点.
(1)分别求出一次函数和反比例函数的表达式;
(2)点P是x轴上一动点,当PE+PF的值最小时,点P的坐标为 .
20.已知点A为函数y=(x>0)图象上任意一点,连接OA并延长至点B,使AB=OA,过点B作BC∥x轴交函数图象于点C,连接OC.
(1)如图1,若点A的坐标为(4,n),求点C的坐标;
(2)如图2,过点A作AD⊥BC,垂足为D,求四边形OCDA的面积.
21.如图,在平面直角坐标系中,Rt△ABC的斜边BC在x轴上,坐标原点是BC的中点,∠ABC=30°,BC=4,双曲线y=经过点A.
(1)求k;
(2)直线AC与双曲线y=﹣在第四象限交于点D,求△ABD的面积.
答案解析部分
一、单选题
1.【答案】 D
【解析】【解答】解:A、∵-1×8=-8≠8,∴该点不在函数图象上,故本选项错误;
B、∵-2×4=-8≠8,∴该点不在函数图象上,故本选项错误;
C、∵1×7=7≠8,∴该点不在函数图象上,故本选项错误;
D、2×4=8,∴该点在函数图象上,故本选项正确.
故答案为:D.
【分析】由于反比例函数y= 中,k=xy,即将各选项横、纵坐标分别相乘,其积为8者即为正确答案.
2.解:因为直线y=mx过原点,双曲线y=的两个分支关于原点对称,
所以其交点坐标关于原点对称,一个交点坐标为(3,4),另一个交点的坐标为(﹣3,﹣4).
故选:C.
3.解:根据图示知,反比例函数y=的图象位于第一、三象限,
∴k>0,
∴一次函数y=kx﹣k的图象与y轴的交点在y轴的负半轴,且该一次函数在定义域内是增函数,
∴一次函数y=kx﹣k的图象经过第一、三、四象限;
故选:B.
4.解:设A的坐标是(m,n),则mn=2.
则AB=m,△ABC的AB边上的高等于n.
则△ABC的面积=mn=1.
故选:A.
5.【答案】 D
【解析】【解答】解:∵在反比例函数y= 中,k=1>0,
∴此函数图象在一、三象限,
∵﹣2<﹣1<0,
∴点A(﹣1,y1),B(﹣2,y2)在第三象限,
∴y1<y2<0,
∵3>0,
∴C(3,y3)点在第一象限,
∴y3>0,
∴y1 , y2 , y3的大小关系为y3>y2>y1 .
故答案为:D.
【分析】先根据函数解析式中的比例系数K,确定函数图像所在的象限,在根据各象限内点的坐标,特征及函数的增减性解答即可。
6.解:∵P是双曲线上一点,且图中△POA的面积为5,
∴k=﹣10,
则反比例函数的解析式为y=﹣,故选:B.
7.解:∵反比例函数y=的图象位于第二、四象限,
∴k<0,﹣k>0.
∵k<0,∴函数y=kx﹣k的图象过二、四象限.
又∵﹣k>0,
∴函数y=kx﹣k的图象与y轴相交于正半轴,
∴一次函数y=kx﹣k的图象过一、二、四象限.故选:B.
8.解:∵反比例函数y=中k>0,
∴函数图象的两个分式分别位于一、三象限,且在每一象限内y随x的增大而减小.
∵﹣2<0,
∴点C(﹣2,y3)位于第三象限,
∴y3<0,
∵0<1<2,
∴点A(1,y1),B(2,y2)位于第一象限,
∴y1>y2>0.
∴y1>y2>y3.故选:D.
9.【答案】 D
【解析】【解答】当 时, ,当 时, ,
∴ .
连接AB并延长AB交x轴于点 ,当P在 位置时, ,即此时 的值最大.
设直线AB的解析式为 ,
将 代入解析式中得
解得 ,
∴直线AB解析式为 .
当 时, ,即 ,
.
故答案为:D.
【分析】先根据反比例函数解析式求出A,B的坐标,然后连接AB并延长AB交x轴于点P’,当P在P'位置时,PA- PB= 4B ,即此时|AP - BP|的值最大,利用待定系数法求出线AB的解析式,从而求出P'的坐标,进而利用面积公式求面积即可.
10.【答案】 C
【解析】【解答】解:①由图象可知: ,
∴ ,故正确;
②从图象上观察可得,不等式 的解集是 或 ,故错误;
④将 , 两点代入 得: ,
即: ,则 ,故正确;
③将 , 代入 得:
,解得: ,
∵ ,
∴ ,
令 ,解得: ,
令 ,解得: ,
∴ , , , ,
∴ , , ,故正确;
∴正确的有:①③④
故答案为:C.
【分析】利用函数图象可知 , 可对①作出判断;由点A,B的横坐标,观察函数图象可得到不等式 的解集,可对②作出判断;将点A,B的坐标代入两函数解析式,可得到 , 可对④作出判断;同时可得到 , 由x=0求出对应的y的值,由y=0求出对应的x的值,可得到点P,Q的坐标,即可得到OQ,OP的长;然后利用三角形的面积公式分别求出△AOP和△BOQ的面积,比较大小,可对③作出判断;综上所述可得到正确结论的序号.
二、填空题
11.解:因为直线y=mx与双曲线y=的交点均关于原点对称,
所以另一个交点坐标为(﹣3,﹣2).
12.解:由题意得:y与x的函数关系式为y==(x>0).
故本题答案为:y=(x>0).
13.解:把(1.5,400)代入双曲线y=,得400=,解得k=600,
则y与x之间的函数关系式为y=;
当x=5时,y==120min.
故答案为:120.
14.解:过F点作FH⊥x轴于H,过E点作EG⊥y轴于G,
∵直线y=﹣x+1与x轴、y轴分别交于A、B,
∴A(1,0),B(0,1),
∴△AOB是等腰直角三角形,
∴△AFH也是等腰直角三角形,△BGE为等腰直角三角形,
∴AH=FH,BG=EG,
∴AF=FH=PM,BE=PN,
∴AF×BE=PM×PN=2PM PN,
∵y=,
∴PM PN=,
∴AF×BE=2PM PN=2×=1.
故答案为1.
15.如图,在平面直角坐标系中,O为坐标原点,MN垂直于x轴,以MN为对称轴作△ODE的轴对称图形,对称轴MN与线段DE相交于点F,点D的对应点B恰好落在y=(k≠0,x<0)的双曲线上,点O、E的对应点分别是点C、A.若点A为OE的中点,且S△AEF=1,则k的值为 ﹣24 .
解:如图,MN交x轴于点G,连接OB,
由于Rt△DOE与Rt△BCA关于MN成轴对称,且OA=AE,
由对称性可知,AG=GE,OA=AE=EC,∴AG=AC,
∵S△AEF=1,∴S△AFG=S△AEF=,
∵MN∥BC∥OD,∴△AFG∽△ABC,
∴=()2=,∴S△ABC=×16=8,
又∵OA=AC,∴S△OAB=S△ABC=4,∴S△OBC=8+4=12,
∵点B在反比例函数y=的图象上,∴S△OBC=12=|k|,
∵k<0,∴k=﹣24,
故答案为:﹣24.
16.如图,A、B两点在反比例函数y=﹣(x<0)的图象上,AB的延长线交x轴于点C,且AB=2BC,则△AOC的面积是 6 .
解:过A作AH⊥OC,过B作BG⊥OC,
∵A、B两点在反比例函数y=﹣(x<0)的图象上,∴设A(x,﹣),S△AOH=,
∵AB=2BC,∴,,∴BG=AH,HG=2CG
∴点B的纵坐标为,代入反比例函数中得点B的坐标为(3x,),
∴OG=﹣3x,HG=﹣2x,CG=﹣x,则OC=﹣4x,
∴S△AOC== (﹣4x) (﹣)=6
故答案为:6.
三、解答题
17.【答案】 解:把点 代入
当 时,
把 , 代入y1=kx+b
,
①-②得,
把 代入①得,
即
.
【解析】【分析】先把A点坐标代入 y2= ,求出反比例函数解析式,接着把 代入反比例函数求出B点坐标,最后把A、B两点坐标代入一次函数 y1=kx+b ,解出k、b即可得到一次函数解析式.
18.【答案】 (1)解: 轴
在 中,
点 在函数 的图象上,
则反比例函数解析式为
在反比例函数 的图象上,
,
将 , 代入 得
代入一次函数解析式得:
解得
则一次函数解析式为
(2)解:当 时,得到 ,即
当 ,即 , ;
当 时, 是线段 的垂直平分线与 轴的交点,
(此处可用两种方法求点 )
方法一:由 得直线 的解析式为 ,线段 中点的坐标为
垂直平分线方程为 ,则
方法二:令垂足为 ,则可证 , ,
即 ,
则
综合可得, 是等腰三角形, 点坐标为 或 或 或
【解析】【分析】(1)根据勾股定理可得OD=3,再利用待定系数法求函数解析式即可;
(2)根据 是等腰三角形 ,分类讨论,结合图象作图求点的坐标即可。
19.如图,在平面直角坐标系中,矩形OABC的两边OC、OA分别在坐标轴上,且OA=2,OC=4,连接OB.反比例函数y=(x>0)的图象经过线段OB的中点D,并与AB、BC分别交于点E、F.一次函数y=k2x+b的图象经过E、F两点.
(1)分别求出一次函数和反比例函数的表达式;
(2)点P是x轴上一动点,当PE+PF的值最小时,点P的坐标为 (,0) .
解:(1)∵四边形OABC为矩形,OA=BC=2,OC=4,
∴B(4,2).
由中点坐标公式可得点D坐标为(2,1),
∵反比例函数y=(x>0)的图象经过线段OB的中点D,
∴k1=xy=2×1=2,
故反比例函数表达式为y=.
令y=2,则x=1;令x=4,则y=.
故点E坐标为(1,2),F(4,).
设直线EF的解析式为y=k2x+b,代入E、F坐标得:
,解得:.
故一次函数的解析式为y=.
(2)作点E关于x轴的对称点E',连接E'F交x轴于点P,则此时PE+PF最小.如图.
由E坐标可得对称点E'(1,﹣2),
设直线E'F的解析式为y=mx+n,代入点E'、F坐标,得:
,解得:.
则直线E'F的解析式为y=,
令y=0,则x=.
∴点P坐标为(,0).
故答案为:(,0).
20.已知点A为函数y=(x>0)图象上任意一点,连接OA并延长至点B,使AB=OA,过点B作BC∥x轴交函数图象于点C,连接OC.
(1)如图1,若点A的坐标为(4,n),求点C的坐标;
(2)如图2,过点A作AD⊥BC,垂足为D,求四边形OCDA的面积.
解:(1)将点A坐标代入到反比例函数y=中得,4n=4,∴n=1,
∴点A的坐标为(4,1),
∵AB=OA,O(0,0),∴点B的坐标为(8,2),
∵BC∥x轴,∴点C的纵坐标为2,
令y=2,则=2,∴x=2,∴点C的坐标为(2,2);
(2)设A(m,),∵AB=OA,∴点B的坐标为(2m,),
∵BC∥x轴,∴BC⊥y轴,
又AD⊥BC,∴AD∥y轴,∴点D的坐标为(),
∵BC∥x轴,且点C在函数图象上,∴C(,),
∵S△OBC= BC =(2m﹣) ==6,S△ADB=BD AD= m =2,
∴四边形OCDA的面积为:S△OBC﹣S△ADB=6﹣2=4.
21.如图,在平面直角坐标系中,Rt△ABC的斜边BC在x轴上,坐标原点是BC的中点,∠ABC=30°,BC=4,双曲线y=经过点A.
(1)求k;
(2)直线AC与双曲线y=﹣在第四象限交于点D,求△ABD的面积.
解:(1)如图,作AH⊥BC于H,
t△ABC的斜边BC在x轴上,坐标原点是BC的中点,∠ABC=30°,BC=4,
∴OC=BC=2,AC=BC×sin30°=2,
∵∠HAC+∠ACO=90°,∠ABC+∠ACO=90°,∴∠HAC=∠ABC=30°,
∴CH=AC×sin30°=1,AH=AC×cos30°=,
∴OH=OC﹣CH=2﹣1=1,∴A(1,),
∵双曲线y=经过点A,∴=,即k=;
(2)设直线AC的解析式为y=kx+b,
∵A(1,),C(2,0),
∴,解得,
∴直线AC的解析式为y=﹣x+2,
∵直线AC与双曲线y=﹣在第四象限交于点D,
∴,解得或,
∵D在第四象限,∴D(3,﹣),
∴S△ABD=S△ABC+S△BCD=BC AH+BC (﹣yD)==4.
一、单选题
1.下列各点中,在反比例函数 图象上的是( )
A. (-1,8) B. (-2,4) C. (1,7) D. (2,4)
2.如图,已知直线y=mx与双曲线y=的一个交点坐标为(3,4),则它们的另一个交点坐标是( )
A.(﹣3,4) B.(﹣4,﹣3) C.(﹣3,﹣4) D.(4,3)
3.如图是反比例函数y=(k为常数,k≠0)的图象,则一次函数y=kx﹣k的图象大致是( )
A.B.C.D.
4.如图,点A是反比例函数(x>0)图象上任意一点,AB⊥y轴于B,点C是x轴上的动点,则△ABC的面积为( )
A.1 B.2 C.4 D.不能确定
5.已知点A(﹣1,y1)、B(﹣2,y2)、C(3,y3)都在反比例函数y= 的图象上,则y1、y2、y3的关系是( )
A. y2>y1>y3 B. y2>y3>y1 C. y3>y1>y2 D. y3>y2>y1
6.如图,P是双曲线上一点,且图中△POA的面积为5,则此反比例函数的解析式为( )
A.y= B.y=﹣ C.y= D.y=
7.函数y=(k≠0)的图象如图所示,那么函数y=kx﹣k的图象大致是( )
A.B.C.D.
8.若点A(1,y1),B(2,y2),C(﹣2,y3)都在反比例函数y=(k>0)的图象上,则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y2<y3<y1 C.y1<y3<y2 D.y3<y2<y1
9.如图所示,已知 为反比例函数 图象上的两点,动点 在 轴正半轴上运动,当 的值最大时,连结 , 的面积是 ( )
A. B. 1 C. D.
10.如图,直线 与 轴、 轴相交于 , 两点,与 的图象相交于 , 两点,连接 , .下列结论:① ;②不等式 的解集是 或 ;③ ;④ .其中正确的结论是( )
A. ①③ B. ②③④ C. ①③④ D. ②④
二、填空题
11.如果直线y=mx与双曲线y=的一个交点A的坐标为(3,2),则它们的另一个交点B的坐标为 .
12.已知一菱形的面积为12cm2,对角线长分别为xcm和ycm,则y与x的函数关系式为
13.码头工人往一艘轮船上装载货物,装完货物所需时间y(min)与装载速度x(t/min)之间的函数关系如图(双曲线y=的一支).如果以5t/min的速度卸货,那么卸完货物需要时间是 min.
14.如图,P为反比例函数y=图象上一点,过点P分别向x轴,y轴引垂线,垂足分别为M、N,直线y=﹣x+1与PM、PN分别交于点E、F,与x轴、y轴分别交于A、B,则AF BE= .
15.如图,在平面直角坐标系中,O为坐标原点,MN垂直于x轴,以MN为对称轴作△ODE的轴对称图形,对称轴MN与线段DE相交于点F,点D的对应点B恰好落在y=(k≠0,x<0)的双曲线上,点O、E的对应点分别是点C、A.若点A为OE的中点,且S△AEF=1,则k的值为 .
16.如图,A、B两点在反比例函数y=﹣(x<0)的图象上,AB的延长线交x轴于点C,且AB=2BC,则△AOC的面积是 .
三、解答题
17.如图,已知一次函数y1=kx+b与反比例函数y2= 的图象交于 、 两点.分别求出y1和y2的解析式.
18.如图所示,在平面直角坐标系中,一次函数 与反比例函数 的图像交于第二、四象限 、 两点,过点 作 轴于点 , , ,且点 的坐标为 .
(1)求一次函数与反比例函数的解析式.
(2) 是 轴上一点,且 是等腰三角形,请直接写出所有符合条件的 点坐标.
19.如图,在平面直角坐标系中,矩形OABC的两边OC、OA分别在坐标轴上,且OA=2,OC=4,连接OB.反比例函数y=(x>0)的图象经过线段OB的中点D,并与AB、BC分别交于点E、F.一次函数y=k2x+b的图象经过E、F两点.
(1)分别求出一次函数和反比例函数的表达式;
(2)点P是x轴上一动点,当PE+PF的值最小时,点P的坐标为 .
20.已知点A为函数y=(x>0)图象上任意一点,连接OA并延长至点B,使AB=OA,过点B作BC∥x轴交函数图象于点C,连接OC.
(1)如图1,若点A的坐标为(4,n),求点C的坐标;
(2)如图2,过点A作AD⊥BC,垂足为D,求四边形OCDA的面积.
21.如图,在平面直角坐标系中,Rt△ABC的斜边BC在x轴上,坐标原点是BC的中点,∠ABC=30°,BC=4,双曲线y=经过点A.
(1)求k;
(2)直线AC与双曲线y=﹣在第四象限交于点D,求△ABD的面积.
答案解析部分
一、单选题
1.【答案】 D
【解析】【解答】解:A、∵-1×8=-8≠8,∴该点不在函数图象上,故本选项错误;
B、∵-2×4=-8≠8,∴该点不在函数图象上,故本选项错误;
C、∵1×7=7≠8,∴该点不在函数图象上,故本选项错误;
D、2×4=8,∴该点在函数图象上,故本选项正确.
故答案为:D.
【分析】由于反比例函数y= 中,k=xy,即将各选项横、纵坐标分别相乘,其积为8者即为正确答案.
2.解:因为直线y=mx过原点,双曲线y=的两个分支关于原点对称,
所以其交点坐标关于原点对称,一个交点坐标为(3,4),另一个交点的坐标为(﹣3,﹣4).
故选:C.
3.解:根据图示知,反比例函数y=的图象位于第一、三象限,
∴k>0,
∴一次函数y=kx﹣k的图象与y轴的交点在y轴的负半轴,且该一次函数在定义域内是增函数,
∴一次函数y=kx﹣k的图象经过第一、三、四象限;
故选:B.
4.解:设A的坐标是(m,n),则mn=2.
则AB=m,△ABC的AB边上的高等于n.
则△ABC的面积=mn=1.
故选:A.
5.【答案】 D
【解析】【解答】解:∵在反比例函数y= 中,k=1>0,
∴此函数图象在一、三象限,
∵﹣2<﹣1<0,
∴点A(﹣1,y1),B(﹣2,y2)在第三象限,
∴y1<y2<0,
∵3>0,
∴C(3,y3)点在第一象限,
∴y3>0,
∴y1 , y2 , y3的大小关系为y3>y2>y1 .
故答案为:D.
【分析】先根据函数解析式中的比例系数K,确定函数图像所在的象限,在根据各象限内点的坐标,特征及函数的增减性解答即可。
6.解:∵P是双曲线上一点,且图中△POA的面积为5,
∴k=﹣10,
则反比例函数的解析式为y=﹣,故选:B.
7.解:∵反比例函数y=的图象位于第二、四象限,
∴k<0,﹣k>0.
∵k<0,∴函数y=kx﹣k的图象过二、四象限.
又∵﹣k>0,
∴函数y=kx﹣k的图象与y轴相交于正半轴,
∴一次函数y=kx﹣k的图象过一、二、四象限.故选:B.
8.解:∵反比例函数y=中k>0,
∴函数图象的两个分式分别位于一、三象限,且在每一象限内y随x的增大而减小.
∵﹣2<0,
∴点C(﹣2,y3)位于第三象限,
∴y3<0,
∵0<1<2,
∴点A(1,y1),B(2,y2)位于第一象限,
∴y1>y2>0.
∴y1>y2>y3.故选:D.
9.【答案】 D
【解析】【解答】当 时, ,当 时, ,
∴ .
连接AB并延长AB交x轴于点 ,当P在 位置时, ,即此时 的值最大.
设直线AB的解析式为 ,
将 代入解析式中得
解得 ,
∴直线AB解析式为 .
当 时, ,即 ,
.
故答案为:D.
【分析】先根据反比例函数解析式求出A,B的坐标,然后连接AB并延长AB交x轴于点P’,当P在P'位置时,PA- PB= 4B ,即此时|AP - BP|的值最大,利用待定系数法求出线AB的解析式,从而求出P'的坐标,进而利用面积公式求面积即可.
10.【答案】 C
【解析】【解答】解:①由图象可知: ,
∴ ,故正确;
②从图象上观察可得,不等式 的解集是 或 ,故错误;
④将 , 两点代入 得: ,
即: ,则 ,故正确;
③将 , 代入 得:
,解得: ,
∵ ,
∴ ,
令 ,解得: ,
令 ,解得: ,
∴ , , , ,
∴ , , ,故正确;
∴正确的有:①③④
故答案为:C.
【分析】利用函数图象可知 , 可对①作出判断;由点A,B的横坐标,观察函数图象可得到不等式 的解集,可对②作出判断;将点A,B的坐标代入两函数解析式,可得到 , 可对④作出判断;同时可得到 , 由x=0求出对应的y的值,由y=0求出对应的x的值,可得到点P,Q的坐标,即可得到OQ,OP的长;然后利用三角形的面积公式分别求出△AOP和△BOQ的面积,比较大小,可对③作出判断;综上所述可得到正确结论的序号.
二、填空题
11.解:因为直线y=mx与双曲线y=的交点均关于原点对称,
所以另一个交点坐标为(﹣3,﹣2).
12.解:由题意得:y与x的函数关系式为y==(x>0).
故本题答案为:y=(x>0).
13.解:把(1.5,400)代入双曲线y=,得400=,解得k=600,
则y与x之间的函数关系式为y=;
当x=5时,y==120min.
故答案为:120.
14.解:过F点作FH⊥x轴于H,过E点作EG⊥y轴于G,
∵直线y=﹣x+1与x轴、y轴分别交于A、B,
∴A(1,0),B(0,1),
∴△AOB是等腰直角三角形,
∴△AFH也是等腰直角三角形,△BGE为等腰直角三角形,
∴AH=FH,BG=EG,
∴AF=FH=PM,BE=PN,
∴AF×BE=PM×PN=2PM PN,
∵y=,
∴PM PN=,
∴AF×BE=2PM PN=2×=1.
故答案为1.
15.如图,在平面直角坐标系中,O为坐标原点,MN垂直于x轴,以MN为对称轴作△ODE的轴对称图形,对称轴MN与线段DE相交于点F,点D的对应点B恰好落在y=(k≠0,x<0)的双曲线上,点O、E的对应点分别是点C、A.若点A为OE的中点,且S△AEF=1,则k的值为 ﹣24 .
解:如图,MN交x轴于点G,连接OB,
由于Rt△DOE与Rt△BCA关于MN成轴对称,且OA=AE,
由对称性可知,AG=GE,OA=AE=EC,∴AG=AC,
∵S△AEF=1,∴S△AFG=S△AEF=,
∵MN∥BC∥OD,∴△AFG∽△ABC,
∴=()2=,∴S△ABC=×16=8,
又∵OA=AC,∴S△OAB=S△ABC=4,∴S△OBC=8+4=12,
∵点B在反比例函数y=的图象上,∴S△OBC=12=|k|,
∵k<0,∴k=﹣24,
故答案为:﹣24.
16.如图,A、B两点在反比例函数y=﹣(x<0)的图象上,AB的延长线交x轴于点C,且AB=2BC,则△AOC的面积是 6 .
解:过A作AH⊥OC,过B作BG⊥OC,
∵A、B两点在反比例函数y=﹣(x<0)的图象上,∴设A(x,﹣),S△AOH=,
∵AB=2BC,∴,,∴BG=AH,HG=2CG
∴点B的纵坐标为,代入反比例函数中得点B的坐标为(3x,),
∴OG=﹣3x,HG=﹣2x,CG=﹣x,则OC=﹣4x,
∴S△AOC== (﹣4x) (﹣)=6
故答案为:6.
三、解答题
17.【答案】 解:把点 代入
当 时,
把 , 代入y1=kx+b
,
①-②得,
把 代入①得,
即
.
【解析】【分析】先把A点坐标代入 y2= ,求出反比例函数解析式,接着把 代入反比例函数求出B点坐标,最后把A、B两点坐标代入一次函数 y1=kx+b ,解出k、b即可得到一次函数解析式.
18.【答案】 (1)解: 轴
在 中,
点 在函数 的图象上,
则反比例函数解析式为
在反比例函数 的图象上,
,
将 , 代入 得
代入一次函数解析式得:
解得
则一次函数解析式为
(2)解:当 时,得到 ,即
当 ,即 , ;
当 时, 是线段 的垂直平分线与 轴的交点,
(此处可用两种方法求点 )
方法一:由 得直线 的解析式为 ,线段 中点的坐标为
垂直平分线方程为 ,则
方法二:令垂足为 ,则可证 , ,
即 ,
则
综合可得, 是等腰三角形, 点坐标为 或 或 或
【解析】【分析】(1)根据勾股定理可得OD=3,再利用待定系数法求函数解析式即可;
(2)根据 是等腰三角形 ,分类讨论,结合图象作图求点的坐标即可。
19.如图,在平面直角坐标系中,矩形OABC的两边OC、OA分别在坐标轴上,且OA=2,OC=4,连接OB.反比例函数y=(x>0)的图象经过线段OB的中点D,并与AB、BC分别交于点E、F.一次函数y=k2x+b的图象经过E、F两点.
(1)分别求出一次函数和反比例函数的表达式;
(2)点P是x轴上一动点,当PE+PF的值最小时,点P的坐标为 (,0) .
解:(1)∵四边形OABC为矩形,OA=BC=2,OC=4,
∴B(4,2).
由中点坐标公式可得点D坐标为(2,1),
∵反比例函数y=(x>0)的图象经过线段OB的中点D,
∴k1=xy=2×1=2,
故反比例函数表达式为y=.
令y=2,则x=1;令x=4,则y=.
故点E坐标为(1,2),F(4,).
设直线EF的解析式为y=k2x+b,代入E、F坐标得:
,解得:.
故一次函数的解析式为y=.
(2)作点E关于x轴的对称点E',连接E'F交x轴于点P,则此时PE+PF最小.如图.
由E坐标可得对称点E'(1,﹣2),
设直线E'F的解析式为y=mx+n,代入点E'、F坐标,得:
,解得:.
则直线E'F的解析式为y=,
令y=0,则x=.
∴点P坐标为(,0).
故答案为:(,0).
20.已知点A为函数y=(x>0)图象上任意一点,连接OA并延长至点B,使AB=OA,过点B作BC∥x轴交函数图象于点C,连接OC.
(1)如图1,若点A的坐标为(4,n),求点C的坐标;
(2)如图2,过点A作AD⊥BC,垂足为D,求四边形OCDA的面积.
解:(1)将点A坐标代入到反比例函数y=中得,4n=4,∴n=1,
∴点A的坐标为(4,1),
∵AB=OA,O(0,0),∴点B的坐标为(8,2),
∵BC∥x轴,∴点C的纵坐标为2,
令y=2,则=2,∴x=2,∴点C的坐标为(2,2);
(2)设A(m,),∵AB=OA,∴点B的坐标为(2m,),
∵BC∥x轴,∴BC⊥y轴,
又AD⊥BC,∴AD∥y轴,∴点D的坐标为(),
∵BC∥x轴,且点C在函数图象上,∴C(,),
∵S△OBC= BC =(2m﹣) ==6,S△ADB=BD AD= m =2,
∴四边形OCDA的面积为:S△OBC﹣S△ADB=6﹣2=4.
21.如图,在平面直角坐标系中,Rt△ABC的斜边BC在x轴上,坐标原点是BC的中点,∠ABC=30°,BC=4,双曲线y=经过点A.
(1)求k;
(2)直线AC与双曲线y=﹣在第四象限交于点D,求△ABD的面积.
解:(1)如图,作AH⊥BC于H,
t△ABC的斜边BC在x轴上,坐标原点是BC的中点,∠ABC=30°,BC=4,
∴OC=BC=2,AC=BC×sin30°=2,
∵∠HAC+∠ACO=90°,∠ABC+∠ACO=90°,∴∠HAC=∠ABC=30°,
∴CH=AC×sin30°=1,AH=AC×cos30°=,
∴OH=OC﹣CH=2﹣1=1,∴A(1,),
∵双曲线y=经过点A,∴=,即k=;
(2)设直线AC的解析式为y=kx+b,
∵A(1,),C(2,0),
∴,解得,
∴直线AC的解析式为y=﹣x+2,
∵直线AC与双曲线y=﹣在第四象限交于点D,
∴,解得或,
∵D在第四象限,∴D(3,﹣),
∴S△ABD=S△ABC+S△BCD=BC AH+BC (﹣yD)==4.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
