第六单元 整理与复习(教案) 数学五年级上册
文档属性
| 名称 | 第六单元 整理与复习(教案) 数学五年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 193.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-16 00:00:00 | ||
图片预览

文档简介
五年级上册六单元整理与复习拓展课教学设计
设计简介
本单元通过动手探究,集体交流,学生掌握了平行四边形、三角形、梯形的面积计算公式以及推导过程,以及组合图形面积的计算和对不规则图形面积进行估计的方法。内容丰富,知识量大,因此有必要让学生对所学内容进行梳理,将知识梳理归纳,总结出具有共性的方法和数学思考,进一步内化,将书由厚读薄。在此基础上,丰富各部分内容独自的特点,丰富认知,将书再由薄读厚,使得学生对学习内容形成一幅网络图,帮助学生深入清晰地复习内容。
二、教学目标
1.进一步理解并巩固平面图形面积的计算方法,并能正确运用公式进行面积的计算。
2.掌握各种平面图形的面积公式之间的联系,使学生形成知识网络。
3.通过对平面图形面积公式之间的关系的研究,强化学生转化的数学思想。
三、教学重点、难点:
教学重点:1.理解平面图形面积计算公式之间的内在联系,完善知识结构体系。
2.灵活运用公式和图形间的关系解决问题。
教学难点:1.掌握“转化”的数学思想,建构知识网络。
2.灵活运用公式和图形间的关系解决问题。
四、教学过程:
(一)开篇点题
最近一段我们一起研究了有关图形面积的知识,今天这节课我们一起对本单元的知识进行整理与复习。(板书课题:图形面积整理与复习(1))
(二)知识梳理
我们以小组为单位,绘制一张思维导图,把五单元的知识进行梳理。
1.现在与你的组员讨论一下,你们打算怎样进行整理。
小组交流,教师巡视。集体汇报,分享交流。
小组绘制,时间15分钟。集体汇报。
汇报要求:(1)清楚地说给大家听;(2)认真倾听,适当补充;(3)人人都要发言。
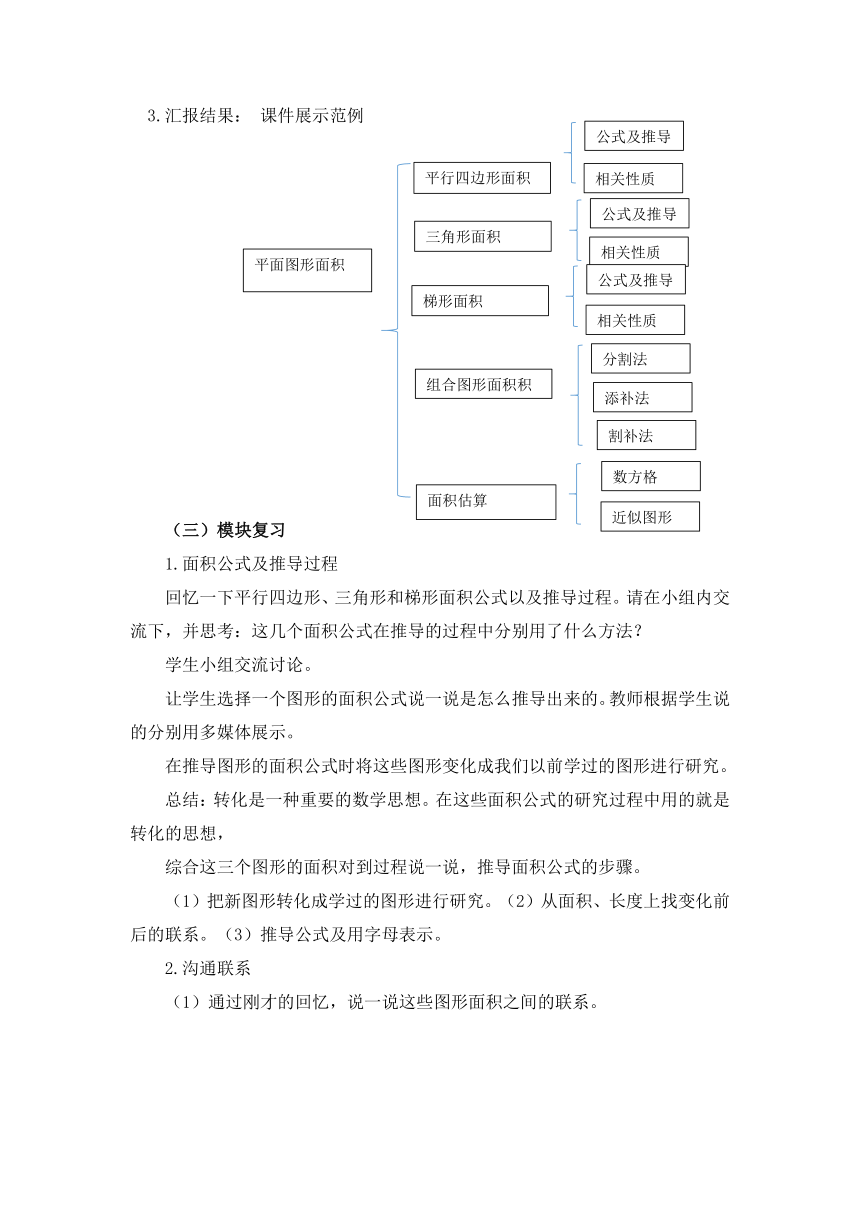
3.汇报结果: 课件展示范例
(三)模块复习
1.面积公式及推导过程
回忆一下平行四边形、三角形和梯形面积公式以及推导过程。请在小组内交流下,并思考:这几个面积公式在推导的过程中分别用了什么方法?
学生小组交流讨论。
让学生选择一个图形的面积公式说一说是怎么推导出来的。教师根据学生说的分别用多媒体展示。
在推导图形的面积公式时将这些图形变化成我们以前学过的图形进行研究。
总结:转化是一种重要的数学思想。在这些面积公式的研究过程中用的就是转化的思想,
综合这三个图形的面积对到过程说一说,推导面积公式的步骤。
(1)把新图形转化成学过的图形进行研究。(2)从面积、长度上找变化前后的联系。(3)推导公式及用字母表示。
2.沟通联系
(1)通过刚才的回忆,说一说这些图形面积之间的联系。
引导:这几种平面图形之间存在着内在的联系。让学生试着用图形表示出它们之间的联系。
预设:正方形、平行四边形面积公式都是在长方形面积的基础上推导出来的,三角形、梯形的面积公式又是在平行四边形面积公式的基础上推导出来的。
练习1.把一个长方形框架拉成一个平行四边形,周长( ),面积( )。(填变大、变小或不变)
解析:将一个长方形框架拉成一个平行四边形,四条边的长度没有变化,所以周长不变,但在过程中平行四边形的高度小于长方形的宽度,所以面积变小。
练习2.将一个平行四边形沿着虚线剪开,拼成一个长方形,那么着两者图形的( )
A. 周长一样;面积一样
B. 周长一样;面积不同
C. 周长不同;面积不同
D. 周长不同;面积一样
解析:用割补法转化图形,面积保持不变。如图可以看出平行四边形周长大于长方形周长。
【设计意图:推拉框架和移多补少都可以将平行四边形和长方形进行相互转化,但其保持不变的性质不同,也是易混淆点。】
练习3.图中涂色部分的面积是( )平方厘米。
A.60 B.90 C.108 D.120
解析:三角形面积面积公式为:底×高÷2.在这里要注意底和高要对应,即相互垂直,观察可知12cm这条高对应的底为10cm。计算面积:10×12÷2=60(平方厘米)。
【设计意图:利用钝角三角形的形外高进行面积计算,本题需要学生找出对应的底和高。】
(2)感受神奇的变化
梯形的面积公式是S=(a+b)×h÷2,你能根据梯形的面积公式推导出其他图形的面积公式吗?想一想,如何将梯形变化成其他图形呢?
指名回答,课件演示。
当梯形的上底和下底相同时,图形就变为一个平行四边形,即S=(a+a)h÷2= ah
当梯形的上底为0时,图形就变为一个三角形,即S=(a+0)h÷2=ah÷2
【设计意图:通过想象找出图形间的相互关系,从而找到公式之间的联系,培养学生的空间想象能力和推理能力。】
3.图形大小的性质。
根据我们所学,发现虽然图形的形状不同,但当他们具备一定的条件时,他们的面积是相等的,请你回忆一下,你知道哪些结论?(教师板书)
预设:①等底等高的平行四边形面积相等;
②等底等高的三角形面积相等。
③上底和下底之和相等,高也相等的梯形面积相等。
你还知道哪些结论?
④等底等高的平行四边形和三角形,平行四边形面积是三角形面积的2倍。
你能在平行线间画出一组这样的图形吗?
练习4下面是4个完全一样的长方形,其中阴影部分的面积( )
只有两个相等 B. 只有三个相等 C.四个都相等 D.四个都不相等
解析:前两个三角形等底等高,第三个三角形与前面的三角形高和底互换,所以面积相等,第四个组合图形可以分割成两个三角形,每个三角形都是所在长方形面积的一半,所以面积之和也为长方形的一半。
练习5.在○里填上“>”“<”或“=”。
甲 乙 甲 乙 甲 乙
五、板书设计:
整理与复习
公式推导策略:转化
①等底等高的平行四边形面积相等;
②等底等高的三角形面积相等。
③上底和下底之和相等,高也相等的梯形面积相等。
④等底等高的平行四边形和三角形,平行四边形面积是三角形的2倍。
设计简介
本单元通过动手探究,集体交流,学生掌握了平行四边形、三角形、梯形的面积计算公式以及推导过程,以及组合图形面积的计算和对不规则图形面积进行估计的方法。内容丰富,知识量大,因此有必要让学生对所学内容进行梳理,将知识梳理归纳,总结出具有共性的方法和数学思考,进一步内化,将书由厚读薄。在此基础上,丰富各部分内容独自的特点,丰富认知,将书再由薄读厚,使得学生对学习内容形成一幅网络图,帮助学生深入清晰地复习内容。
二、教学目标
1.进一步理解并巩固平面图形面积的计算方法,并能正确运用公式进行面积的计算。
2.掌握各种平面图形的面积公式之间的联系,使学生形成知识网络。
3.通过对平面图形面积公式之间的关系的研究,强化学生转化的数学思想。
三、教学重点、难点:
教学重点:1.理解平面图形面积计算公式之间的内在联系,完善知识结构体系。
2.灵活运用公式和图形间的关系解决问题。
教学难点:1.掌握“转化”的数学思想,建构知识网络。
2.灵活运用公式和图形间的关系解决问题。
四、教学过程:
(一)开篇点题
最近一段我们一起研究了有关图形面积的知识,今天这节课我们一起对本单元的知识进行整理与复习。(板书课题:图形面积整理与复习(1))
(二)知识梳理
我们以小组为单位,绘制一张思维导图,把五单元的知识进行梳理。
1.现在与你的组员讨论一下,你们打算怎样进行整理。
小组交流,教师巡视。集体汇报,分享交流。
小组绘制,时间15分钟。集体汇报。
汇报要求:(1)清楚地说给大家听;(2)认真倾听,适当补充;(3)人人都要发言。
3.汇报结果: 课件展示范例
(三)模块复习
1.面积公式及推导过程
回忆一下平行四边形、三角形和梯形面积公式以及推导过程。请在小组内交流下,并思考:这几个面积公式在推导的过程中分别用了什么方法?
学生小组交流讨论。
让学生选择一个图形的面积公式说一说是怎么推导出来的。教师根据学生说的分别用多媒体展示。
在推导图形的面积公式时将这些图形变化成我们以前学过的图形进行研究。
总结:转化是一种重要的数学思想。在这些面积公式的研究过程中用的就是转化的思想,
综合这三个图形的面积对到过程说一说,推导面积公式的步骤。
(1)把新图形转化成学过的图形进行研究。(2)从面积、长度上找变化前后的联系。(3)推导公式及用字母表示。
2.沟通联系
(1)通过刚才的回忆,说一说这些图形面积之间的联系。
引导:这几种平面图形之间存在着内在的联系。让学生试着用图形表示出它们之间的联系。
预设:正方形、平行四边形面积公式都是在长方形面积的基础上推导出来的,三角形、梯形的面积公式又是在平行四边形面积公式的基础上推导出来的。
练习1.把一个长方形框架拉成一个平行四边形,周长( ),面积( )。(填变大、变小或不变)
解析:将一个长方形框架拉成一个平行四边形,四条边的长度没有变化,所以周长不变,但在过程中平行四边形的高度小于长方形的宽度,所以面积变小。
练习2.将一个平行四边形沿着虚线剪开,拼成一个长方形,那么着两者图形的( )
A. 周长一样;面积一样
B. 周长一样;面积不同
C. 周长不同;面积不同
D. 周长不同;面积一样
解析:用割补法转化图形,面积保持不变。如图可以看出平行四边形周长大于长方形周长。
【设计意图:推拉框架和移多补少都可以将平行四边形和长方形进行相互转化,但其保持不变的性质不同,也是易混淆点。】
练习3.图中涂色部分的面积是( )平方厘米。
A.60 B.90 C.108 D.120
解析:三角形面积面积公式为:底×高÷2.在这里要注意底和高要对应,即相互垂直,观察可知12cm这条高对应的底为10cm。计算面积:10×12÷2=60(平方厘米)。
【设计意图:利用钝角三角形的形外高进行面积计算,本题需要学生找出对应的底和高。】
(2)感受神奇的变化
梯形的面积公式是S=(a+b)×h÷2,你能根据梯形的面积公式推导出其他图形的面积公式吗?想一想,如何将梯形变化成其他图形呢?
指名回答,课件演示。
当梯形的上底和下底相同时,图形就变为一个平行四边形,即S=(a+a)h÷2= ah
当梯形的上底为0时,图形就变为一个三角形,即S=(a+0)h÷2=ah÷2
【设计意图:通过想象找出图形间的相互关系,从而找到公式之间的联系,培养学生的空间想象能力和推理能力。】
3.图形大小的性质。
根据我们所学,发现虽然图形的形状不同,但当他们具备一定的条件时,他们的面积是相等的,请你回忆一下,你知道哪些结论?(教师板书)
预设:①等底等高的平行四边形面积相等;
②等底等高的三角形面积相等。
③上底和下底之和相等,高也相等的梯形面积相等。
你还知道哪些结论?
④等底等高的平行四边形和三角形,平行四边形面积是三角形面积的2倍。
你能在平行线间画出一组这样的图形吗?
练习4下面是4个完全一样的长方形,其中阴影部分的面积( )
只有两个相等 B. 只有三个相等 C.四个都相等 D.四个都不相等
解析:前两个三角形等底等高,第三个三角形与前面的三角形高和底互换,所以面积相等,第四个组合图形可以分割成两个三角形,每个三角形都是所在长方形面积的一半,所以面积之和也为长方形的一半。
练习5.在○里填上“>”“<”或“=”。
甲 乙 甲 乙 甲 乙
五、板书设计:
整理与复习
公式推导策略:转化
①等底等高的平行四边形面积相等;
②等底等高的三角形面积相等。
③上底和下底之和相等,高也相等的梯形面积相等。
④等底等高的平行四边形和三角形,平行四边形面积是三角形的2倍。
