人教版八年级数学下册19.2.3 一次函数与方程、不等式同步练习(word版含答案)
文档属性
| 名称 | 人教版八年级数学下册19.2.3 一次函数与方程、不等式同步练习(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 368.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-17 08:17:45 | ||
图片预览



文档简介
八下_第19章 一次函数_19.2 一次函数_19.2.3 一次函数与方程、不等式
一、选择题(共3小题;共15分)
1. 已知一元一次方程 (, 为常数,)的解为 ,那么一次函数 的函数值为 时,自变量 的值是
A. B. C. D.
2. 如果函数 ,那么 与 的大小关系为
A. B.
C. D. 不能确定
3. 用图象法解某二元一次方程组时,在同一直角坐标系中作出相应的两个一次函数的图象(如图所示),则所解的二元一次方程组是
A. B.
C. D.
二、填空题(共6小题;共33分)
4. 如图,在 中,,,则 .
5. 如图,已知函数 的图象过点 ,则不等式 的解集是 .
6. 已知函数 和 ,当 时,;当 时,,当 时,,直线 与 的交点坐标为 .
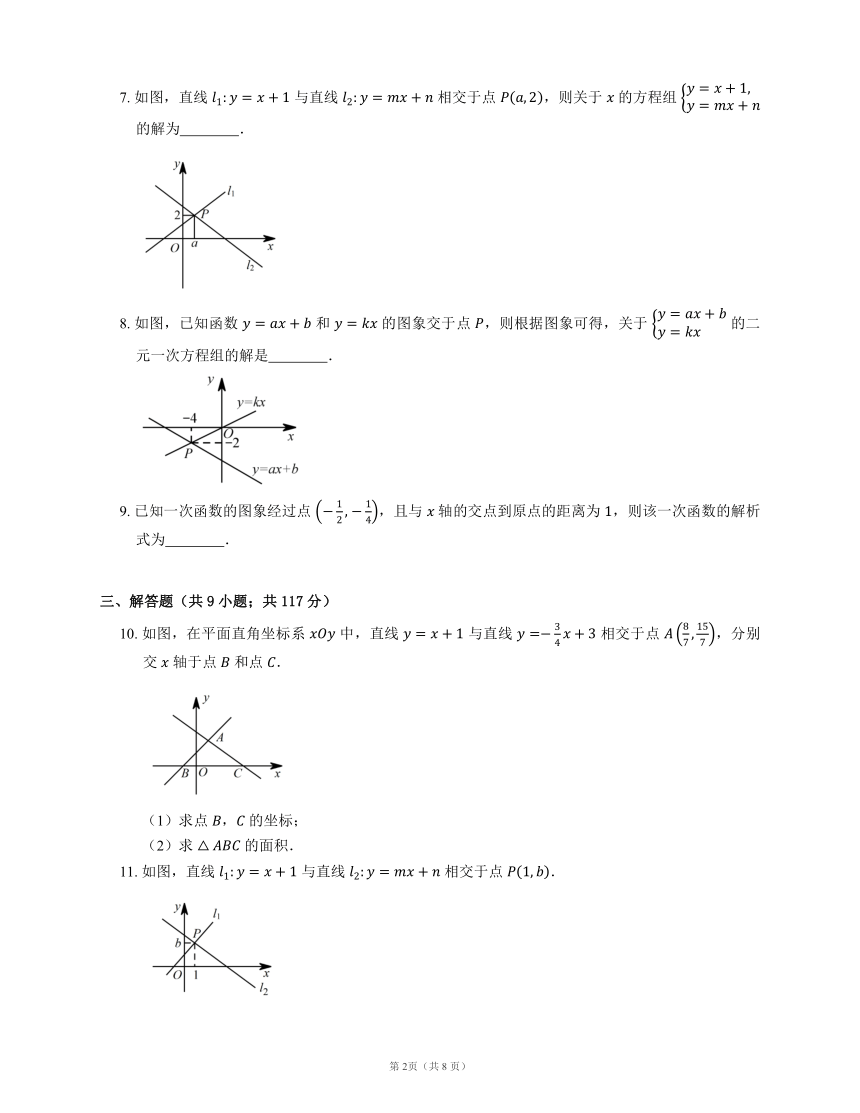
7. 如图,直线 与直线 相交于点 ,则关于 的方程组 的解为 .
8. 如图,已知函数 和 的图象交于点 ,则根据图象可得,关于 的二元一次方程组的解是 .
9. 已知一次函数的图象经过点 ,且与 轴的交点到原点的距离为 ,则该一次函数的解析式为 .
三、解答题(共9小题;共117分)
10. 如图,在平面直角坐标系 中,直线 与直线 相交于点 ,分别交 轴于点 和点 .
(1)求点 , 的坐标;
(2)求 的面积.
11. 如图,直线 与直线 相交于点 .
(1)求 的值.
(2)不解关于 , 的方程组 直接写出它的解.
(3)直线 是否也经过点 说明理由.
12. 若一次函数 的图象经过直线 和 的交点,求 的值.
13. 某游泳馆普通票价为 元/张,暑假为了促销,新推出两种优惠卡:
①金卡售价 元/张,每次凭卡不再收费;
②银卡售价 元/张,每次凭卡另收 元.
暑期普通票正常出售,两种优惠卡仅限暑期使用,不限次数.设游泳 次时,所需总费用为 元.
(1)分别写出选择银卡、普通票消费时, 与 之间的函数关系式;
(2)在同一个坐标系中,若三种消费方式对应的函数图象如图所示,请求出点 ,, 的坐标;
(3)请根据函数图象,直接写出选择哪种消费方式更合算.
14. 某电子厂家经过市场调查,发现一种计算器的供应量 (万个)与价格 (万元)之间的关系如图中供应线所示,而需求量 (万个)与价格 (万元)之间的关系如图中需求线所示,如果你是这个电子厂厂长,应计划生产这种计算器多少个,每一万个售价多少万元,才能使市场达到供需平衡
15. 取什么整数时,直线 与直线 的交点在第二象限
16. 如图,直线 的表达式为 ,且 与 轴交于点 ,直线 经过点 ,,直线 , 交于点 .
(1)求点 的坐标;
(2)求直线 的表达式;
(3)求 的面积.
17. 某校实行学案式教学,需印制若干份教学学案.印刷厂有甲、乙两种收费方式,除按印数收取印刷费用外,甲种方式还需收取制版费,而乙种方式不需要制版费.两种收费方式的费用 (元)与印刷份数 (份)之间的关系如图所示:
(1)甲种收费方式的函数关系式是 ,乙种收费方式的函数关系式是 ;
(2)该校某年级每次印刷 (含 和 )份学案,选择哪种收费方式较合算
18. 已知一次函数 的图象经过点 .
(1)请直接写出 , 满足的关系式为 ;
(2)若 时, 有最大值 ,求 的值.
答案
第一部分
1. C
2. C
3. D
第二部分
4.
【解析】,,
.
是 的外角,
.
.
.
5.
6. ,,,,,,,
7.
8.
9. 或
【解析】由题意可知一次函数的图象与 轴的交点坐标为 或 .
设一次函数的解析式为 (),
当一次函数图象过点 , 时,
由 解得
此时一次函数的解析式为 ;
当一次函数图象过点 , 时,
由 解得
此时一次函数的解析式为 .
综上所述,该一次函数的解析式为 或 .
第三部分
10. (1) 直线 与 轴交于点 ,当 时,,解得 ,所以点 的坐标是 .
直线 与 轴交于点 ,当 时,,解得 .
所以点 的坐标是 .
(2) 因为 ,点 到 轴的距离为 ,
所以 .
11. (1) 因为点 在直线 上,将点 坐标代入 ,得 ,所以 的值为 .
(2) 方程组 的解就是直线 与直线 的交点 的坐标.由()知,,所以方程组 的解为
(3) 直线 也经过点 .理由如下:
因为点 在直线 上,将点 坐标代入直线方程得 ,对于 ,当 时,有 ,即当 时,,所以直线 也经过点 .
12. 由 和 组成的方程组为 解得
将 , 代入 ,得 ,解得 .
13. (1) 普通票消费时,;
银卡消费时,.
(2) 把 代入 ,得 ,
.
由题意列方程组 解得
.
把 代入 ,得 ,
.
(3) 当 时, 段最低,
时,普通票消费更划算;
时,选择银卡和普通票消费的总费用相同,均比金卡消费合算;
当 时, 段最低,
时,银卡消费更划算;
时,选择银卡和金卡消费的总费用相同,均比普通票合算;
时,金卡消费更划算.
14. 设供应线对应的一次函数为 ,由题意,得
解得
所以 .
设需求线对应的一次函数为 ,由题意,得
解得
所以 .
由
解得
所以当生产这种计算器 万个,每一万个售价为 万元时,能使市场达到供需平衡.
15. 由题意得 解得
所以这两条直线的交点坐标为 .
因为交点在第二象限,
所以有 解这个不等式组,得 .
又因为 是整数,
所以 或 .
所以当 取 或 时,两直线的交点在第二象限.
16. (1) 在函数 中,令 ,得 ,解得 ,
所以点 的坐标为 .
(2) 设直线 的表达式为 ,由题中图象知 时,, 时,,
所以有
解得
所以直线 的表达式为 .
(3) 联立
解得
所以点 的坐标为 .
因为 ,
所以 .
17. (1) ;
(2) 由 ,得 .
由 ,得 .
由 ,得 .
由此可知当 时,
选择乙种收费方式比较合算;
当 时,选择甲、乙两种收费方式一样;
当 时,选择甲种收费方式比较合算.
18. (1)
(2) ①当 时, 有最大值 ,则 ,
解得 ;
②当 时, 有最大值 ,则 ,
解得 ;
故若 时, 有最大值 , 的值为 或 .
第1页(共1 页)
一、选择题(共3小题;共15分)
1. 已知一元一次方程 (, 为常数,)的解为 ,那么一次函数 的函数值为 时,自变量 的值是
A. B. C. D.
2. 如果函数 ,那么 与 的大小关系为
A. B.
C. D. 不能确定
3. 用图象法解某二元一次方程组时,在同一直角坐标系中作出相应的两个一次函数的图象(如图所示),则所解的二元一次方程组是
A. B.
C. D.
二、填空题(共6小题;共33分)
4. 如图,在 中,,,则 .
5. 如图,已知函数 的图象过点 ,则不等式 的解集是 .
6. 已知函数 和 ,当 时,;当 时,,当 时,,直线 与 的交点坐标为 .
7. 如图,直线 与直线 相交于点 ,则关于 的方程组 的解为 .
8. 如图,已知函数 和 的图象交于点 ,则根据图象可得,关于 的二元一次方程组的解是 .
9. 已知一次函数的图象经过点 ,且与 轴的交点到原点的距离为 ,则该一次函数的解析式为 .
三、解答题(共9小题;共117分)
10. 如图,在平面直角坐标系 中,直线 与直线 相交于点 ,分别交 轴于点 和点 .
(1)求点 , 的坐标;
(2)求 的面积.
11. 如图,直线 与直线 相交于点 .
(1)求 的值.
(2)不解关于 , 的方程组 直接写出它的解.
(3)直线 是否也经过点 说明理由.
12. 若一次函数 的图象经过直线 和 的交点,求 的值.
13. 某游泳馆普通票价为 元/张,暑假为了促销,新推出两种优惠卡:
①金卡售价 元/张,每次凭卡不再收费;
②银卡售价 元/张,每次凭卡另收 元.
暑期普通票正常出售,两种优惠卡仅限暑期使用,不限次数.设游泳 次时,所需总费用为 元.
(1)分别写出选择银卡、普通票消费时, 与 之间的函数关系式;
(2)在同一个坐标系中,若三种消费方式对应的函数图象如图所示,请求出点 ,, 的坐标;
(3)请根据函数图象,直接写出选择哪种消费方式更合算.
14. 某电子厂家经过市场调查,发现一种计算器的供应量 (万个)与价格 (万元)之间的关系如图中供应线所示,而需求量 (万个)与价格 (万元)之间的关系如图中需求线所示,如果你是这个电子厂厂长,应计划生产这种计算器多少个,每一万个售价多少万元,才能使市场达到供需平衡
15. 取什么整数时,直线 与直线 的交点在第二象限
16. 如图,直线 的表达式为 ,且 与 轴交于点 ,直线 经过点 ,,直线 , 交于点 .
(1)求点 的坐标;
(2)求直线 的表达式;
(3)求 的面积.
17. 某校实行学案式教学,需印制若干份教学学案.印刷厂有甲、乙两种收费方式,除按印数收取印刷费用外,甲种方式还需收取制版费,而乙种方式不需要制版费.两种收费方式的费用 (元)与印刷份数 (份)之间的关系如图所示:
(1)甲种收费方式的函数关系式是 ,乙种收费方式的函数关系式是 ;
(2)该校某年级每次印刷 (含 和 )份学案,选择哪种收费方式较合算
18. 已知一次函数 的图象经过点 .
(1)请直接写出 , 满足的关系式为 ;
(2)若 时, 有最大值 ,求 的值.
答案
第一部分
1. C
2. C
3. D
第二部分
4.
【解析】,,
.
是 的外角,
.
.
.
5.
6. ,,,,,,,
7.
8.
9. 或
【解析】由题意可知一次函数的图象与 轴的交点坐标为 或 .
设一次函数的解析式为 (),
当一次函数图象过点 , 时,
由 解得
此时一次函数的解析式为 ;
当一次函数图象过点 , 时,
由 解得
此时一次函数的解析式为 .
综上所述,该一次函数的解析式为 或 .
第三部分
10. (1) 直线 与 轴交于点 ,当 时,,解得 ,所以点 的坐标是 .
直线 与 轴交于点 ,当 时,,解得 .
所以点 的坐标是 .
(2) 因为 ,点 到 轴的距离为 ,
所以 .
11. (1) 因为点 在直线 上,将点 坐标代入 ,得 ,所以 的值为 .
(2) 方程组 的解就是直线 与直线 的交点 的坐标.由()知,,所以方程组 的解为
(3) 直线 也经过点 .理由如下:
因为点 在直线 上,将点 坐标代入直线方程得 ,对于 ,当 时,有 ,即当 时,,所以直线 也经过点 .
12. 由 和 组成的方程组为 解得
将 , 代入 ,得 ,解得 .
13. (1) 普通票消费时,;
银卡消费时,.
(2) 把 代入 ,得 ,
.
由题意列方程组 解得
.
把 代入 ,得 ,
.
(3) 当 时, 段最低,
时,普通票消费更划算;
时,选择银卡和普通票消费的总费用相同,均比金卡消费合算;
当 时, 段最低,
时,银卡消费更划算;
时,选择银卡和金卡消费的总费用相同,均比普通票合算;
时,金卡消费更划算.
14. 设供应线对应的一次函数为 ,由题意,得
解得
所以 .
设需求线对应的一次函数为 ,由题意,得
解得
所以 .
由
解得
所以当生产这种计算器 万个,每一万个售价为 万元时,能使市场达到供需平衡.
15. 由题意得 解得
所以这两条直线的交点坐标为 .
因为交点在第二象限,
所以有 解这个不等式组,得 .
又因为 是整数,
所以 或 .
所以当 取 或 时,两直线的交点在第二象限.
16. (1) 在函数 中,令 ,得 ,解得 ,
所以点 的坐标为 .
(2) 设直线 的表达式为 ,由题中图象知 时,, 时,,
所以有
解得
所以直线 的表达式为 .
(3) 联立
解得
所以点 的坐标为 .
因为 ,
所以 .
17. (1) ;
(2) 由 ,得 .
由 ,得 .
由 ,得 .
由此可知当 时,
选择乙种收费方式比较合算;
当 时,选择甲、乙两种收费方式一样;
当 时,选择甲种收费方式比较合算.
18. (1)
(2) ①当 时, 有最大值 ,则 ,
解得 ;
②当 时, 有最大值 ,则 ,
解得 ;
故若 时, 有最大值 , 的值为 或 .
第1页(共1 页)
