人教版八年级数学下册19.3 课题学习 选择方案同步练习(word版含解析)
文档属性
| 名称 | 人教版八年级数学下册19.3 课题学习 选择方案同步练习(word版含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 192.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-17 00:00:00 | ||
图片预览



文档简介
八下_第19章 一次函数_19.3 课题学习 选择方案
一、填空题(共3小题;共15分)
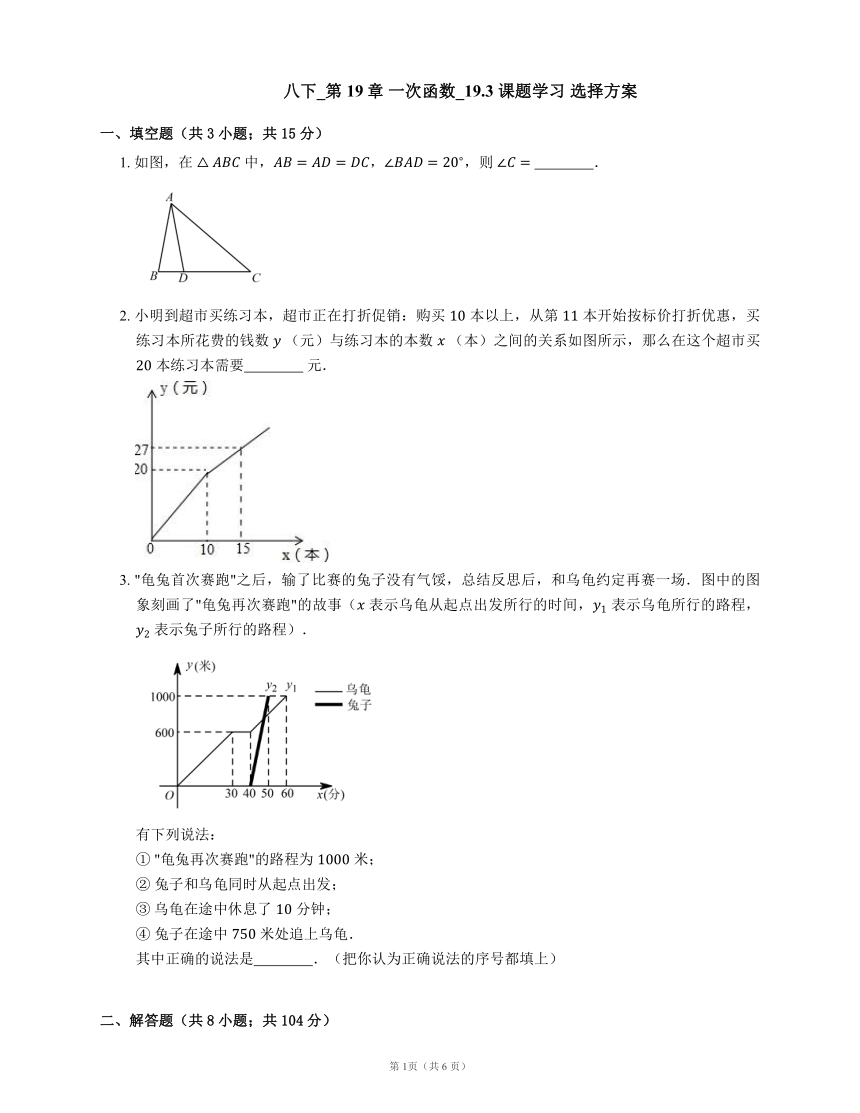
1. 如图,在 中,,,则 .
2. 小明到超市买练习本,超市正在打折促销:购买 本以上,从第 本开始按标价打折优惠,买练习本所花费的钱数 (元)与练习本的本数 (本)之间的关系如图所示,那么在这个超市买 本练习本需要 元.
3. "龟兔首次赛跑"之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的图象刻画了"龟兔再次赛跑"的故事( 表示乌龟从起点出发所行的时间, 表示乌龟所行的路程, 表示兔子所行的路程).
有下列说法:
① "龟兔再次赛跑"的路程为 米;
② 兔子和乌龟同时从起点出发;
③ 乌龟在途中休息了 分钟;
④ 兔子在途中 米处追上乌龟.
其中正确的说法是 .(把你认为正确说法的序号都填上)
二、解答题(共8小题;共104分)
4. 某校准备在甲、乙两家公司为毕业班学生制作一批纪念册.甲公司提出:每册收材料费 元,另收设计费 元;乙公司提出:每册收材料费 元,不收设计费.
(1)制作纪念册册数 与甲公司的收费 (元)之间的函数关系式为 ;
(2)制作纪念册册数 与乙公司的收费 (元)之间的函数关系式为 ;
(3)如果学校派你去订做纪念册,怎样选择公司,才能使费用最省.
5. “黄金一号”玉米种子的价格为 ,一次购买 以上的种子,超过 部分的种子的价格打八折.
(1)根据题意,填写下表:
(2)设购买种子的质量为 ,付款金额为 元,求 关于 的函数关系式;
(3)若小张一次购买该种子花费了 元,求他购买种子的质量.
6. 为解决用电紧张的矛盾,某电力公司制订了新的用电收费标准,每月用电量 (千瓦时)与应付电费 (元)的关系如图所示.
(1)根据图象,请分别求出当 和 时, 与 的函数关系式: , .
(2)请回答:
①当每月用电量不超过 千瓦时时,收费标准是 ;
②当每月用电量超过 千瓦时时,收费标准是 .
7. 小刚家装修,准备安装照明灯.他和爸爸到市场进行调查,了解到某种优质品牌的一盏 瓦白炽灯的售价为 元,一盏 瓦节能灯的售价为 元,这两种功率的灯发光效果相当.假定电价为 元/千瓦时,设照明时间为 (时),使用一盏白炽灯和一盏节能灯的费用分别为 (元)和 (元)[耗电量(千瓦时) 功率(千瓦) 用电时间(时),费用 电费 灯的售价].
(1)分别求出 , 与照明时间 之间的函数表达式;
(2)你认为选择哪种照明灯合算
(3)若一盏白炽灯的使用寿命为 小时,一盏节能灯的使用寿命为 小时,不考虑其他因素,以 小时计算,使用哪种照明灯省钱 省多少钱
8. 某公司推销一种新产品,设 (件)是推销新产品的数量,(元)是推销费,下图表示了公司每月付给推销员推销费的两种方案.根据下图解答下列问题:
(1)求 , 与 之间的函数关系式;
(2)解释图中表示的两种方案是如何付推销费的;
(3)如果你是推销员,应该如何选择
9. 联通公司手机话费收费有A套餐(月租费 元,通话费每分钟 元)和B套餐(月租费 元,通话费每分钟 元)两种.设 A套餐每月话费为 (元),B套餐每月话费为 (元),月通话时间为 分钟.
(1)分别表示出 , 与 的函数关系式.
(2)月通话时间为多长时,A,B两种套餐收费一样
(3)什么情况下A套餐更省钱
10. 一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,设客车到乙地的距离为 千米,出租车到甲地的距离为 千米.两车行驶的时间为 小时, 与 关于 的函数图象如图所示.
(1)根据图象直接写出 , 关于 的函数解析式.
(2)若两车之间的距离为 千米,请写出 关于 的函数关系式.
(3)甲、乙两地间有A,B两个加油站,相距 千米,若客车进入A加油站时,出租车恰好进入B加油站.求A加油站到甲地的距离.
11. 小明到服装店参加社会实践活动,服装店经理让小明帮助解决以下问题:
服装店准备购进甲乙两种服装,甲种每件进价 元,售价 元;乙种每件进价 元,售价 元.计划购进两种服装共 件,其中甲种服装不少于 件.
(1)若购进这 件服装的费用不得超过 元,则甲种服装最多购进多少件
(2)在()的条件下,该服装店对甲种服装以每件优惠 元的价格进行优惠促销,乙种服装价格不变,那么该服装店应如何调整进货方案才能获得最大利润
答案
第一部分
1.
【解析】,,
.
是 的外角,
.
.
.
2.
【解析】提示:由题意知 本以上的函数解析式为
当 时, .
3. ①③④
【解析】如图,路程为 米,①正确;
兔子比乌龟晚出发 分钟,②错误;
乌龟从 到 分钟时,路程一直是 米,中途休息了 分钟,③正确;
(),,
兔子和乌龟相遇时,,解得 ,,④正确.
第二部分
4. (1)
(2)
(3) 当册数超过 时,选择甲公司;
当册数等于 时,选择甲、乙两家公司均可;
当册数小于 时,选择乙公司.
5. (1) ;
(2) 根据题意,当 时,.
当 时,其中有 的种子按 计价,其余的 种子按 (即 折)计价,
,
关于 的函数关系式为 .
(3) ,
一次购买种子的质量超过 ,
,解得 .
答:小张购买了 种子.
6. (1) ;
(2) ① 元 /千瓦时;②其中的 千瓦时按每千瓦时 元收费,超过部分按每千瓦时 元收费
7. (1) 根据题意,得 ,即 .
,即 .
(2) 由 ,得 ,解得 .
由 ,得 ,解得 .
由 ,得 ,解得 .
当照明时间为 小时时,选择两种灯的费用相同;当照明时间超过 小时时,选择节能灯合算;当照明时间少于 小时时,选择白炽灯合算.
(3) 由()知,当 小时时,使用节能灯省钱.
当 时,(元),
当 时,(元),
(元).
按 小时计算,使用节能灯省钱,省 元.
8. (1) ,.
(2) 是不推销产品没有推销费,每推销 件产品得推销费 元, 是保底工资 元,每推销 件产品再提成 元.
(3) 若业务能力强,平均每月能保证推销 件以上时,就选择 的方案,否则选择 的方案.
9. (1) .
.
(2) 由
得
答:当月通话时间是 分钟时,A,B两种套餐收费一样.
(3) 当月通话时间多于 分钟时,A套餐更省钱.
10. (1) ,
.
(2) .
(3) 由题意知 .
①当 时,,
,
.
②当 时,
,
,
.
③当 时,,不合题意.
A 加油站到甲地的距离为 千米或 千米.
11. (1) 设购进甲种服装 件,
由题意可知
解得
答:甲种服装最多购进 件.
(2) 设总利润为 元,
因为甲种服装不少于 件,
所以 .
.
方案 :当 时,, 随 的增大而增大,
所以当 时, 有最大值,则购进甲种服装 件,乙种服装 件;
方案 :当 时,所有方案获利相同,
所以按哪种方案进货都可以;
方案 :当 时,, 随 的增大而减小,
所以当 时, 有最大值,则购进甲种服装 件,乙种服装 件.
第1页(共1 页)
一、填空题(共3小题;共15分)
1. 如图,在 中,,,则 .
2. 小明到超市买练习本,超市正在打折促销:购买 本以上,从第 本开始按标价打折优惠,买练习本所花费的钱数 (元)与练习本的本数 (本)之间的关系如图所示,那么在这个超市买 本练习本需要 元.
3. "龟兔首次赛跑"之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的图象刻画了"龟兔再次赛跑"的故事( 表示乌龟从起点出发所行的时间, 表示乌龟所行的路程, 表示兔子所行的路程).
有下列说法:
① "龟兔再次赛跑"的路程为 米;
② 兔子和乌龟同时从起点出发;
③ 乌龟在途中休息了 分钟;
④ 兔子在途中 米处追上乌龟.
其中正确的说法是 .(把你认为正确说法的序号都填上)
二、解答题(共8小题;共104分)
4. 某校准备在甲、乙两家公司为毕业班学生制作一批纪念册.甲公司提出:每册收材料费 元,另收设计费 元;乙公司提出:每册收材料费 元,不收设计费.
(1)制作纪念册册数 与甲公司的收费 (元)之间的函数关系式为 ;
(2)制作纪念册册数 与乙公司的收费 (元)之间的函数关系式为 ;
(3)如果学校派你去订做纪念册,怎样选择公司,才能使费用最省.
5. “黄金一号”玉米种子的价格为 ,一次购买 以上的种子,超过 部分的种子的价格打八折.
(1)根据题意,填写下表:
(2)设购买种子的质量为 ,付款金额为 元,求 关于 的函数关系式;
(3)若小张一次购买该种子花费了 元,求他购买种子的质量.
6. 为解决用电紧张的矛盾,某电力公司制订了新的用电收费标准,每月用电量 (千瓦时)与应付电费 (元)的关系如图所示.
(1)根据图象,请分别求出当 和 时, 与 的函数关系式: , .
(2)请回答:
①当每月用电量不超过 千瓦时时,收费标准是 ;
②当每月用电量超过 千瓦时时,收费标准是 .
7. 小刚家装修,准备安装照明灯.他和爸爸到市场进行调查,了解到某种优质品牌的一盏 瓦白炽灯的售价为 元,一盏 瓦节能灯的售价为 元,这两种功率的灯发光效果相当.假定电价为 元/千瓦时,设照明时间为 (时),使用一盏白炽灯和一盏节能灯的费用分别为 (元)和 (元)[耗电量(千瓦时) 功率(千瓦) 用电时间(时),费用 电费 灯的售价].
(1)分别求出 , 与照明时间 之间的函数表达式;
(2)你认为选择哪种照明灯合算
(3)若一盏白炽灯的使用寿命为 小时,一盏节能灯的使用寿命为 小时,不考虑其他因素,以 小时计算,使用哪种照明灯省钱 省多少钱
8. 某公司推销一种新产品,设 (件)是推销新产品的数量,(元)是推销费,下图表示了公司每月付给推销员推销费的两种方案.根据下图解答下列问题:
(1)求 , 与 之间的函数关系式;
(2)解释图中表示的两种方案是如何付推销费的;
(3)如果你是推销员,应该如何选择
9. 联通公司手机话费收费有A套餐(月租费 元,通话费每分钟 元)和B套餐(月租费 元,通话费每分钟 元)两种.设 A套餐每月话费为 (元),B套餐每月话费为 (元),月通话时间为 分钟.
(1)分别表示出 , 与 的函数关系式.
(2)月通话时间为多长时,A,B两种套餐收费一样
(3)什么情况下A套餐更省钱
10. 一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,设客车到乙地的距离为 千米,出租车到甲地的距离为 千米.两车行驶的时间为 小时, 与 关于 的函数图象如图所示.
(1)根据图象直接写出 , 关于 的函数解析式.
(2)若两车之间的距离为 千米,请写出 关于 的函数关系式.
(3)甲、乙两地间有A,B两个加油站,相距 千米,若客车进入A加油站时,出租车恰好进入B加油站.求A加油站到甲地的距离.
11. 小明到服装店参加社会实践活动,服装店经理让小明帮助解决以下问题:
服装店准备购进甲乙两种服装,甲种每件进价 元,售价 元;乙种每件进价 元,售价 元.计划购进两种服装共 件,其中甲种服装不少于 件.
(1)若购进这 件服装的费用不得超过 元,则甲种服装最多购进多少件
(2)在()的条件下,该服装店对甲种服装以每件优惠 元的价格进行优惠促销,乙种服装价格不变,那么该服装店应如何调整进货方案才能获得最大利润
答案
第一部分
1.
【解析】,,
.
是 的外角,
.
.
.
2.
【解析】提示:由题意知 本以上的函数解析式为
当 时, .
3. ①③④
【解析】如图,路程为 米,①正确;
兔子比乌龟晚出发 分钟,②错误;
乌龟从 到 分钟时,路程一直是 米,中途休息了 分钟,③正确;
(),,
兔子和乌龟相遇时,,解得 ,,④正确.
第二部分
4. (1)
(2)
(3) 当册数超过 时,选择甲公司;
当册数等于 时,选择甲、乙两家公司均可;
当册数小于 时,选择乙公司.
5. (1) ;
(2) 根据题意,当 时,.
当 时,其中有 的种子按 计价,其余的 种子按 (即 折)计价,
,
关于 的函数关系式为 .
(3) ,
一次购买种子的质量超过 ,
,解得 .
答:小张购买了 种子.
6. (1) ;
(2) ① 元 /千瓦时;②其中的 千瓦时按每千瓦时 元收费,超过部分按每千瓦时 元收费
7. (1) 根据题意,得 ,即 .
,即 .
(2) 由 ,得 ,解得 .
由 ,得 ,解得 .
由 ,得 ,解得 .
当照明时间为 小时时,选择两种灯的费用相同;当照明时间超过 小时时,选择节能灯合算;当照明时间少于 小时时,选择白炽灯合算.
(3) 由()知,当 小时时,使用节能灯省钱.
当 时,(元),
当 时,(元),
(元).
按 小时计算,使用节能灯省钱,省 元.
8. (1) ,.
(2) 是不推销产品没有推销费,每推销 件产品得推销费 元, 是保底工资 元,每推销 件产品再提成 元.
(3) 若业务能力强,平均每月能保证推销 件以上时,就选择 的方案,否则选择 的方案.
9. (1) .
.
(2) 由
得
答:当月通话时间是 分钟时,A,B两种套餐收费一样.
(3) 当月通话时间多于 分钟时,A套餐更省钱.
10. (1) ,
.
(2) .
(3) 由题意知 .
①当 时,,
,
.
②当 时,
,
,
.
③当 时,,不合题意.
A 加油站到甲地的距离为 千米或 千米.
11. (1) 设购进甲种服装 件,
由题意可知
解得
答:甲种服装最多购进 件.
(2) 设总利润为 元,
因为甲种服装不少于 件,
所以 .
.
方案 :当 时,, 随 的增大而增大,
所以当 时, 有最大值,则购进甲种服装 件,乙种服装 件;
方案 :当 时,所有方案获利相同,
所以按哪种方案进货都可以;
方案 :当 时,, 随 的增大而减小,
所以当 时, 有最大值,则购进甲种服装 件,乙种服装 件.
第1页(共1 页)
