沪科版八年级上册13.2 一次函数(共8课时)
文档属性
| 名称 | 沪科版八年级上册13.2 一次函数(共8课时) |

|
|
| 格式 | zip | ||
| 文件大小 | 7.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-14 00:00:00 | ||
图片预览











文档简介
课件90张PPT。 1、某种汽油3.60元/l.加油 x l,应付y元,那么y与x 之间的函数关系式是?y=3.60x 2、某同学家住县城,离校约3000米,骑自行车回家每分钟行驶300米,若x表示骑车离家的时间(分钟),y 表示离家的路程,你能写出y与x之间的关系式吗?
y=3000-300x 3、电信公司推出市话服务,收费标准为月租费25元,本地网通话费为每分钟0.1元.若x表示通话时间(分钟),y表示通话的应缴的费用(元) ,你能写出y与x的函数关系式吗? y=25+0.1x⑴ y =3.60x
(2) y=3000-300x
(3) y=25+0.1x
1、这些函数中自变量是什么?
函数是什么?2、在这些函数式中,表示函数的自变量的式子,是关于自变量的几次式?上述函数关系式有什么共同的特点?
当b=0时,称y是x的正比例函数。
即:y=kx(k是常数,k≠ 0) 一次函数:若两个变量 x、y之间的关系可以表示成y=kx+b(k、b为常数,k ≠ 0)的形式,则称 y是x的一次函数。例1:下列函数关系式中,那些是一次函数?哪些是正比例函数?(1)y= – x – 4
(2)y = x2
(3)y = 2πx
(4)y =
它是一次函数,
不是正比例函数。它不是一次函数,
也不是正比例函数。它是一次函数,
也是正比例函数。它不是一次函数,
也不是正比例函数? 例2: 已知函数y=(m+1)x+(m2-1),当m取什么值时, y是x的一次函数?当m取什么值时,y是x的正比例函数?解:(1)∵ y是x的一次函数(2) ∵ y是x的正比例函数
又∵ m≠ -1 ∴ m=1一次函数y=kx+b中的k ≠ 0特别提醒!即 m≠-1∴ m+1 ≠ 0m=1或-1∴ m2-1=0
巩固:
已知函数y=(n+3)x +(n2-9),当n取什么值时, y是x的一次函数?当n取什么值时,y是x的正比例函数?
议一议、比一比:
若y=(m2-1)x2+(m+1)x(m为常数)是正比例函数,求m的值.
解: ∵ y是 x的正比例函数
∴ m+1 ≠ 0 即 m≠-1
又∵ m2-1=0 ∴ m=1 或-1
综上所得 m=1
写出下列变化过程中y与x之间的函数关系式,并判断y是否为x的一次函数?是否为正比例函数?(1)正方形面积y与边长x之间的函数关系:(2)正方形周长y与边长x之间的函数关系:y=4xy=x2(3)长方形的长为常量a时,面积y与宽x之间的函数关系:y=ax不是一次函数是一次函数,也是正比例函数是一次函数,也是正比例函数(4)某同学中午在学校食堂就餐,每餐用去3.5元。午餐费用y元与就餐次数x之间的函数关系。
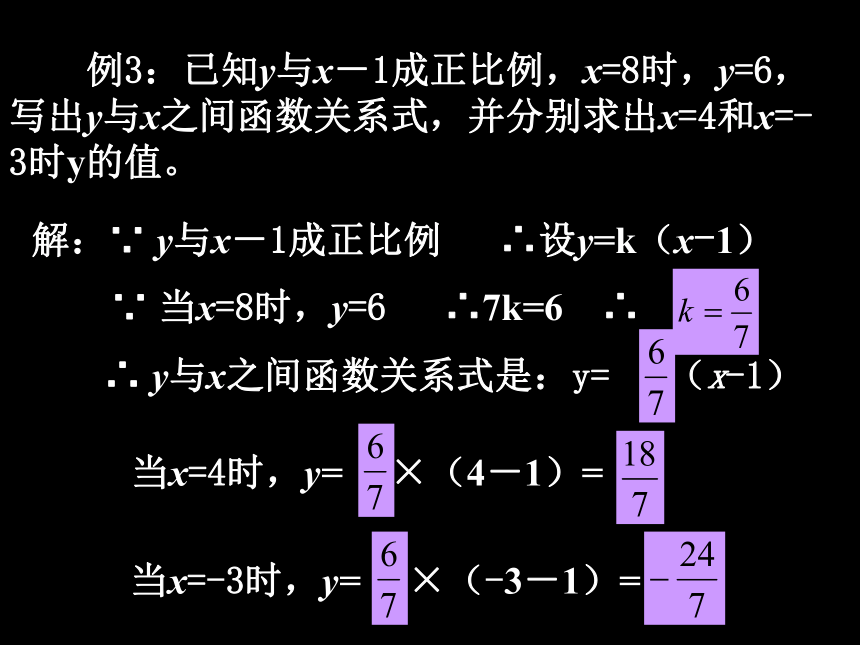
y=3.5x (5)一棵树现在高5 0 厘米,每个月长高2 厘米,x 月后这棵树的高度为y 厘米。y=50+2x是一次函数,也是正比例函数是一次函数,但不是正比例函数 例3:已知y与x-1成正比例,x=8时,y=6,写出y与x之间函数关系式,并分别求出x=4和x=-3时y的值。解:∵ y与x-1成正比例 ∴设y=k(x-1) 当x=4时,y= ×(4-1)=当x=-3时,y= ×(-3-1)=∵ 当x=8时,y=6 ∴7k=6 ∴∴ y与x之间函数关系式是:y= (x-1) 2、已知y=y1+y2,y1与x2成正比例,y2与x -2成正比例,当x=1时,y=0,当x =-3时,y=4,求x =3时,y的值。拓展练习1、填空
(1)若y=5x3m-2是正比例函数,m= 。(2)若 是正比例函数m= 。(3)若y=(m-1)xm2是关于 x的正比例函数,则m= .
(4)已知一个正比例函数的比例系数是-5,则它的解析式为: 。1-2-1y= -5x下列函数中哪些是正比例函数?(2)y = x+2(1)y =2x(5)y=x2+1 (3)(4)(6)是是不是不是不是不是 随堂练习-4-2024y=2x例1: 画正比例函数 y =2x 的图象解:1. 列表2. 描点3. 连线……y=2x 画出正比例函数 , , 的图象? 正比例函数y= kx (k≠0) 的图象是1k当k>0时,1k当k<0时, 经过原点(0,0)和点(1,k)的一条直线。y=kx (k>0)y=kx (k<0)直线y=kx 经过第一、三象限及原点;直线y=kx 经过第二、四象限及原点。过这两点画直线,例2:画函数 的图象当k>0时直线y=kx经过一,三象限及原点,x增大时,y的值也增大;当k<0时,直线y=kx经过二,四象限及原点,x增大时,y的值反而减小。24 y = 2x 1224y随x的增大而增大y随x的增大而减小-3-6 一般地,正比例函数y=kx(k是常数,k≠0)的图象是一条经过原点的直线,我们称它为直线y=kx.当k >0时,直线y=kx经过第三、一象限及原点,从左向右上升,即随着x的增大y也增大;当k <0时,直线y=kx经过第二、四象限及原点,从左向右下降,即随着x的增大y反而减小. 1.函数y=-7x的图象在第 象限内,经过点(0, )与点(1, ),y随x的增大而 .二、四0-7减小 2、正比例函数y=(k+1)x的图像中y随x 的增大而增大,则k的取值范围是 。k> - 1 3.正比例函数y=(m-1)x的图象经过一、三象限,则m的取值范围是( )
A.m=1 B.m>1 C.m<1 D.m≥1B 4、若正比例函数y=(1-3m)x的图像经过点A(x1,y1)和B(x2,y2),当x1<x2时,y1 >y2,则m的取值范围是 。 5、直线y=(k2+3)x经过 象限,y随x的减小而 。一、三减小小结正比例函数1、定义: 一般地,形如 y=kx(k是常数,k≠0)的函数,叫做正比例函数,其中 k 叫做比例系数.2、图像过原点(0,0)和(1,k)的一条直线3、性质当k>0时,直线y=kx经过一、三象限及原点,y随 x增大而增大;当k<0时,直线y=kx经过二、四象限及原点,y 随x增大而减小。感悟:时间是一个“常量”,但对于勤奋者来说,却是一个“变量”,我们应该在有限的时间内做出伟大的事业!
你的收获与你的付出是成正比的,一份耕耘一份收获,相信自己,只要付出,你一定会有收获!1.一次函数的一般形式
y=kx+b (k,b是常数,k≠0)
正比例函数的一般形式
y=kx (k是常数,k≠0)
二者有什么联系?
正比例函数是一次函数b=0时的特殊情况
2.根据函数解析式画图,有哪几步?
列表描点连线旧知复习画出函数y= -2x+3的图象2+3
=50+3=3 - 2+3
=1 -4+3
= -1讨论交流一(1)对于自变量x的同一个值,一次函数y = -2x+3的函数值与函数y = -2x的函数值相比,有什么特点?
(2)说出点A(2,-1)到点B(2,2)是怎么平移的?
(口答)y= - 2xy= - 2x+3 观察上面两个函数图象的相同点与不同点,与同桌交流一下,谈谈自己的见解。讨论交流二(2分钟) 1、这两个函数的图象都是 ,并且它们的位置关系是 。
2、函数y=﹣2x的图象经过原点,函数y=-2x+3的图象与y轴交于点_______即它可以看作直线y=-2x向 平移 个单位长度而得到.直线平行上3(0,3) 直线y=-2x向下平移3个单位长度可得到函数 的图象观察图象中点的变化:y=-2x -3y=-2xy=-2x+3y=-2x-3一次函数y=kx+b的图象是 ,它可由正比例函数y=kx_____ 得到
当b>0时,直线向 平移∣b∣个单位长度
当b<0时,直线向 平移∣b∣个单位长度一条直线平移上下归纳小结: 1.将直线y=3x向下平移2个单位得到 直线_____________。 y=3x-2 2.将直线y=-x-5向上平移5个单位,得到直线____________。y =-x 3.函数y=kx-4的图像平行于直线y =-2x,则其函数的表达式为____________。y= -2x -4认识截距 1、请根据图像分别写出一次函数y = -2x+3与一次函数y=-2x -3的图像与y轴的交点坐标。 2、直线y =kx + b与y轴的交点坐标是什么?(0,b)合作时间一(两分钟) 请同桌之间互相给对方写一个一次函数的解析式,并指出对方所写一次函数的图像与y轴的交点坐标以及截距。 直线y=kx+b与y轴相交于点( 0,b ),b叫做直线y=kx+b在y轴上的截距,简称截距。 “截距”不是 “截得的距离”,它只是直线y=kx+b与y轴交点的纵坐标的值,如直线y=2x-7的截距是-7
注意:讨论交流三 1、在平面直角系中确定一条直线需要几个点? 2、画一次函数的图像你会找哪两个点?和你的同桌讨论,取哪两个点画图时比较方便? 3、你能直接利用函数解析式求函数图象与坐标轴交点的坐标吗?应用新知 例1:画出直线 并求出它的截距。解:对于 有截距:-2-2300(0, -2)(3,0) 同学们,本节课你学到了那些内容呢?请大家相互交流,总结所学的知识点。
1.一次函数y=kx+b的图像也是一条直线。
(画图像时,需考虑自变量的取值范围)
2.一次函数y=kx+b的图像可以通过平移正比例函数y=kx的图像得到。(两者图像之间的关系)
3.截距课堂小结:一.复习:
1.作函数图像的步骤是什么?(1)列表 (2)描点 (3)连线2.一次函数图像的特点是什么? 是一条直线,所以我们在作一次图像的时候只需要确定两个点,再过这两个点作直线就可以了。-6o-446246-2-2-4xy2y=0.5xy=xy=3xy=-2x(1)上面的函数都是什么函数?(2)正比例函数y=kx的
图象有什么特点?(3) y随x的增减性 ?经过的象限?(4)直线的倾斜程度 ? 正比例函数正比例函数y=kx的图象是经
过(0,0),(1,k)的一条直线k>0,过一、三象限及原点,
y随x的增大而增大;
k<0,过二、四象限及原点,
y随x的增大而减小; |k|越大,越接近y轴;| k |越小,越接近x轴y=-x 一次函数y=kx+b的图像是平行于直线y=kx的一条直线。所以,我们把一次函数y = kx +b的图像叫做直线y = kx +b 。
同时,一次函数y=kx+b的图像可由直线y=kx平移∣b∣个单位长度而得到(b>0,向上平移;b<0,向下平移)。复习回顾: 1、直线y=2x+5与直线y=-3x+5都经过y轴上的同一点( , )
2、直线y=2x -3,可以由直线y=2x +1经过
向 个单位而得到。直线 y=-3x可以由直线y=-3x -2 经过向 个单位而得到
3、已知直线y=kx+b平行于直线
且通过点(0,-3),求此函数的解析式。巩固训练0 5下平移4上平移2画出一次函数 的图象 01y-1.50x观察分析: 当一个点在直线上从左向右移动时,它的位置怎样变化 自变量x由___到___函数y的值从___到___大小小大y随x的增大而增大,
这时函数的图象从左到右上升; 的图象 观察分析: 自变量x由___到___函数y的值从___到___大小小大y随x的增大而减小,
这时函数的图象从左到右下降; y=-x+2 一次函数y=kx+b有下列性质:
?
(1) 当k>0时,y随x的增大而_____ ,这时函数的图象从左到右_____ ;
?
(2) 当k <0时, y随x的增大而_____,这时函数的图象从左到右_____. 概括减小下降增大上升六.探索发现(1) 在同一坐标系中作出下列函数的图象
(1)(2)(3)-3o-223123-1-1-2xy1思考:k、b的值跟图像的位置有什么关系?(2)在同一坐标系中作出下列函数的图象(1)(2)(3)-3o-223123-1-1-2xy1思考:k、b的值跟图像的位置有什么关系?结论k >ob=0b>0b<0b=0b>0b<0 通过作以上一次函数的图像我们发现y=kx+b
中,k,b的取值跟图像的关系如下:k <0一、三一、二、三一、三、四二、四一、二、四二、三、四当k >0时,y的值随x的增大而增大当k <0时,y的值随x的增大而减小根据图象确定k,b的取值K 0
b 0K 0
b 0K 0
b 0K 0
b 0K 0
b 0K 0
b 0K
b>
=<
=<
><
<>
<>
>
1 一次函数y=x-2的图象不经过的象限为( )
(A) 一 (B) 二 (C) 三 (D) 四
2 不经过第二象限的直线是 ( )
y=-2x+4 (B) y=2x-1
(C) y=2x+1 (D) y=-2x+1
3 若直线 y=kx+b经过一二四象限,那么直线 y=-bx+k经过 象限
4 直线 y=kx-k的图象的大致位置是 ( )
ABCDBB二、三、四C1.求出下列函数的解析式
(1)将直线y=5x向下平移6个单位;
(2)将直线 向上平移3个单位.
2.已知一次函数y=(1-2k)x+(2k+1)
(1)当k取何值时,y随x的增大而增大?
(2)当k取何值时,函数图象经过坐标系原点?
(3)当k取何值时,函数图象不经过第四象限?快马加鞭56结论一次函数的图象特征:
一次函数y=k x +b是经过(0,b)和( ,0)的一条直线一次函数y=kx+b性质:k>0时,y随x的增大而增大;
k<0时, y随x的增大而减小。直线y=kx+b是过点(0,b)且平行于直线y=kx的
一条直线正比例函数的图象特征:
是经过(0,0)和(1,k)两点的一条直线.
正比例函数的图象的性质:
(1)当k>0时,y随x的增大而增大;
(2)当k<0时,y随x的增大而减小.59结论:回味练习:
1、函数y=2x图象经过点(0, )与点(1, ),y随x的增大而 ;2、函数y=(a-2)x的图象经过第二、四象限,则a的范围是 ;
3、函数y=(1- k) x中y随x的增大而减小,则k的范围是 .02增大a<2k>14、直线y=-3x-6与x轴的交点坐标是 ,与y轴的交点坐标为 .(-2,0)(0,-6)5、直线y=3x-1经过 象限;
直线y=-2x+5经过 象限.
一、三、四一、二、四6、直线y=kx+b(k<0,b<0)经过 象限。
7、若直线y=kx+b经过一、二、四象限,则k 0,
b 0.
8、直线y=kx+b的图象如图所示,确定k、b符号:xx二、三、四<>K<0,b>0k>0,b<0
(1)已知直线y=kx+b平行于直线y=-2x+1,且过点(-2,4),分别求出k和b。
(2)一次函数y=4x-3和y=-4x-3的图象分别经过________象限和_______象限,它们的交点坐标是______.
(3)已知一次函数y=(2-m)x+m+2,那么
(a)当m为何值时,它的图象经过原点;
(b)当m为何值时,它的图象经过点(-1,5);
(c)当m为何值时,它的图象不经过第二象限。巩固练习:如何求一次函数的解析式例1、已知y与x成正比例,其图象过点( ,1),
求此函数的解析式。引申:
(1)、已知:y与x -1成正比例,且当x =-5时,y=3,求y与x之间的函数关系式。(2)、已知:y与z成正比例,z+1与x成正比例,且当x =1时,y=1;当x =0时,y=-3。
求y与x的函数关系式。(3)已知y与x成正比例,若y随x的增大而减小,且其图象经过(4,-a)和(a,-1)两点,求y与x之间的函数关系式。例2、已知:一次函数y=kx+b的图象经过点(5,-2)和(2,1)两点,求此一次函数的解析式。变式:已知y是x的一次函数,且其图象过点(5,-2)和(2,1),求其解析式。引申:
(1)已知:直线y=k x +b平行于直线y=2 x ,且经过点(-1,2),求y与x之间的函数关系式。(2)已知直线y=2x +b与两坐标轴围成的面积为4,求此函数的解析式。(3)已知一次函数的图象经过点(0,3),且与两坐标轴围成的面积为 ,求函数的解析式。
回味练习: 1.已知一次函数的图象经过点( 3 , 5 )和(-4,-9),求这个一次函数的解析式. 3.已知一次函数的图象经过点(-3 , 1)和(1,-5),求当x =5时,函数y的值. 4.若一次函数的图像与直线y =-3x+2交y轴与同一点,且过点(2,-6),求此一次函数的解析式. 2.已知直线y1=kx+b与直线y2 =-2x平行,且直线y1在y轴上的截距为2,求直线y1的解析式.例3、已知y=y1+y2,其中y1与x成正比例,y2与(x -2)成正比例,又当x=-1时,y=2;当x=2时,y=5. 求y与x的函数关系式。例4、根据图象,求出相应的函数关系式: 例5、已知一次函数的图象经过直线 y=-x+5与x轴的交点,且与y轴 的交点的纵坐标是-3,求函数的解析式。 例6、已知:点P是一次函数y=-2x+8的图象上一点,如果图象与x轴交于Q点,且△OPQ的面积等于6,求P点的坐标。回味练习:
1.函数y=2x-1与x轴交点坐标为_______ ,与y轴交点坐标为____,与两坐标轴围成的三角形面积是______.
2.若直线y=kx+b和直线y=-x平行,与y轴交点的纵坐标为-2,则直线的解析式为_______.
3.已知一次函数的图象经过点A(2,-1)
和点B,B是另一直线 与y轴的
交点,这个一次函数的解析式___________.( ,0)(0,-1)引申:
1.求直线y=2x+4与x轴、y轴 的交点坐标.
2.求直线y=2x-4与直线y=-x+1的交点坐标.
3.若直线y=ax-2与直线y=bx+1的图象交于x轴上同一点,则a:b=_____.
4. m为何值时,直线y=2x+m与 的交点横坐标为1.思考1:
若一次函数的图象交x轴于点A(- 6,0),交正比例函数的图象于点B,且点B在第二象限,它的横坐标为-4,又知:S△AOB=15,求直线AB的解析式。A(-6,0)(-4, ) By思考2:已知直线y=2x+m与两坐标轴围成的三角形面积为4,求m.变:已知直线y=kx+2与两坐标轴围成的 三角形面积为2,求k.
若过点(3,0)呢?若过点(2,1)呢? 1、小明从家里出发去菜地浇水,又去玉米地锄草,然后回家,其中x表示时间,y表示小明离他家的距离。 该图表示的函数是正比例函数吗?
是一次函数吗?你是怎样认为的? 2、小芳以200米/分钟的速度起跑后,先匀加速跑5分钟,每分钟提高速度20米/分,又匀速跑10分钟,请写出这段时间里她的跑步速度y(米/分钟)随跑步时间x(分钟)变化的函数关系式。 解:跑步的速度 y (米/分)随跑步时间 x (分钟)变化的函数关系式为: 上述函数,称为分段函数。y=20x+200y =300 3、为加强公民的节水意识,某城市制定了以下用水收费标准:每户每月用水未超过8立方米时,每立方米收取1元并加收0.3元的城市污水处理费;超过8立方米的部分每立方米收取1.5元并加收1.2元的城市污水处理费.设一户每月用水量为x立方米,应缴水费为y元,(1)给出y关于x的函数关系式;
(2)画出上述函数图象;
(8,10.4)●(3)该市一户某月若用水量为x=5立方米或x=10立方米时,求应缴水费;
(4)该市一户某月缴水费26.6元,求该户这月用水量. 自变量的不同取值范围内表示函数关系的解析式有不同的形式,这样的函数称为分段函数。归纳小结:巩固训练 1.某市出租车的计价方式为:开始3km内收费6元,以后每增加1km(不足1km,以1km计)加收1元。
(1)写出乘车路程xkm与收费y元的关系式;
(2)小明乘车5km,应付多少钱?7.6呢?
(3)小飞乘车付了15元,他至多乘车走了多远?
2.妈妈在用洗衣机洗涤衣服时,经历了进水、清洗、排水、脱水四个连续过程,其中进水、清洗、排水时洗衣机中的水量 y ( l )与时间 x (min)之间的关系如图所示,根据图象解答下列问题: ⑴你能根据图象获得哪些信息?(尽可能多的说出来)
⑵你能分别求出线段OA、AB、BC所表示的y与x之间的函数关系式吗?巩固训练挑战中考 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系. 根据图象进行以下探究:
(1)甲、乙两地之间的距离 为 km900(2)请解释图中B点的实际意义 图中B点的实际意义是:当慢车行驶4h时,慢车和快车相遇. 挑战中考 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系. 由图象可知,慢车12h行驶的路程为900km,所以慢车的速度为:(3)求慢车和快车的速度;900÷12=75(km/h) 当慢车行驶4h时,慢车和快车相遇,两车行驶的路程之和为900km,所以慢车和快车行驶的速度之和为:900÷4=225(km/h)挑战中考 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系. (4)求线段BC所表示的y与 x之间的函数关系式,并写出自变量的取值范围; 根据题意,快车行驶900km到达乙地,所以快车行驶900÷150=6(h)到达乙地,此时两车之间的距离为6×75=450(km),所以点C的坐标为(6,450).∴线段BC的函数关系式为y=225x-900 (4≤x≤6) 6×姚明的脚——你知道姚明的脚有多大吗? 姚明穿的鞋是56码,你能算出他的脚大约有多少厘米长吗? 鞋码与厘米转换表你如何算出姚明“56”码的脚有多少厘米?猜想函数关系:根据题意:解得得出函数关系:验证函数关系:x(cm)y(码)2m-10y=kx+by=2x -10 如图,多边形ABCDEF各角都为直角,动点P以 2cm/s 速度沿图甲的边框按B→C→D→E→F→A的路径移动,相应的△ABP的面积s关于时间t的函数图象如图乙.若AB=6cm,试回答下列问题: ostab6496cm2cm/s图甲图乙GHQ(7)M点坐标是否可以求出?N点坐标是否可以求出?
MN所在直线的函数关系式呢?ostab6496cm2cm/s(1)P点在整个的移动过程中△ABP的面积是怎样变化的?问题:(2)图甲中BC的长是多少?8cm(5)图乙中的a在图甲中具有什么实际意义?a的值是多少? 24(6)图乙中的b在图甲中具有什么实际意义?b的值是多少? (3)图甲中CD的长是多少?(4)图甲中DE的长是多少?4cm6cm42MN···图甲图乙小GHQ 如图,矩形ABCD中,AB=6cm,动点P以2cm/s速度沿图甲的边框按B→C→D→A的路径移动,相应的△ABP的面积s关于时间 t的函数图象如图乙.根据下图回答问题: 问题: (1)P点在整个的移动过程中△ABP的面积是怎样变化的? (3)图乙中的a在图甲中具有什么实际意义?a的值是多少? 10cm30(2)图甲中BC的长是多少?图甲图乙p 成功就是99%的汗水,加上1%的灵感。
------爱迪生 在科学上从没有平坦的大道,只有不畏艰险勇于攀登的人,才能达到光辉的顶点
马克思
y=3000-300x 3、电信公司推出市话服务,收费标准为月租费25元,本地网通话费为每分钟0.1元.若x表示通话时间(分钟),y表示通话的应缴的费用(元) ,你能写出y与x的函数关系式吗? y=25+0.1x⑴ y =3.60x
(2) y=3000-300x
(3) y=25+0.1x
1、这些函数中自变量是什么?
函数是什么?2、在这些函数式中,表示函数的自变量的式子,是关于自变量的几次式?上述函数关系式有什么共同的特点?
当b=0时,称y是x的正比例函数。
即:y=kx(k是常数,k≠ 0) 一次函数:若两个变量 x、y之间的关系可以表示成y=kx+b(k、b为常数,k ≠ 0)的形式,则称 y是x的一次函数。例1:下列函数关系式中,那些是一次函数?哪些是正比例函数?(1)y= – x – 4
(2)y = x2
(3)y = 2πx
(4)y =
它是一次函数,
不是正比例函数。它不是一次函数,
也不是正比例函数。它是一次函数,
也是正比例函数。它不是一次函数,
也不是正比例函数? 例2: 已知函数y=(m+1)x+(m2-1),当m取什么值时, y是x的一次函数?当m取什么值时,y是x的正比例函数?解:(1)∵ y是x的一次函数(2) ∵ y是x的正比例函数
又∵ m≠ -1 ∴ m=1一次函数y=kx+b中的k ≠ 0特别提醒!即 m≠-1∴ m+1 ≠ 0m=1或-1∴ m2-1=0
巩固:
已知函数y=(n+3)x +(n2-9),当n取什么值时, y是x的一次函数?当n取什么值时,y是x的正比例函数?
议一议、比一比:
若y=(m2-1)x2+(m+1)x(m为常数)是正比例函数,求m的值.
解: ∵ y是 x的正比例函数
∴ m+1 ≠ 0 即 m≠-1
又∵ m2-1=0 ∴ m=1 或-1
综上所得 m=1
写出下列变化过程中y与x之间的函数关系式,并判断y是否为x的一次函数?是否为正比例函数?(1)正方形面积y与边长x之间的函数关系:(2)正方形周长y与边长x之间的函数关系:y=4xy=x2(3)长方形的长为常量a时,面积y与宽x之间的函数关系:y=ax不是一次函数是一次函数,也是正比例函数是一次函数,也是正比例函数(4)某同学中午在学校食堂就餐,每餐用去3.5元。午餐费用y元与就餐次数x之间的函数关系。
y=3.5x (5)一棵树现在高5 0 厘米,每个月长高2 厘米,x 月后这棵树的高度为y 厘米。y=50+2x是一次函数,也是正比例函数是一次函数,但不是正比例函数 例3:已知y与x-1成正比例,x=8时,y=6,写出y与x之间函数关系式,并分别求出x=4和x=-3时y的值。解:∵ y与x-1成正比例 ∴设y=k(x-1) 当x=4时,y= ×(4-1)=当x=-3时,y= ×(-3-1)=∵ 当x=8时,y=6 ∴7k=6 ∴∴ y与x之间函数关系式是:y= (x-1) 2、已知y=y1+y2,y1与x2成正比例,y2与x -2成正比例,当x=1时,y=0,当x =-3时,y=4,求x =3时,y的值。拓展练习1、填空
(1)若y=5x3m-2是正比例函数,m= 。(2)若 是正比例函数m= 。(3)若y=(m-1)xm2是关于 x的正比例函数,则m= .
(4)已知一个正比例函数的比例系数是-5,则它的解析式为: 。1-2-1y= -5x下列函数中哪些是正比例函数?(2)y = x+2(1)y =2x(5)y=x2+1 (3)(4)(6)是是不是不是不是不是 随堂练习-4-2024y=2x例1: 画正比例函数 y =2x 的图象解:1. 列表2. 描点3. 连线……y=2x 画出正比例函数 , , 的图象? 正比例函数y= kx (k≠0) 的图象是1k当k>0时,1k当k<0时, 经过原点(0,0)和点(1,k)的一条直线。y=kx (k>0)y=kx (k<0)直线y=kx 经过第一、三象限及原点;直线y=kx 经过第二、四象限及原点。过这两点画直线,例2:画函数 的图象当k>0时直线y=kx经过一,三象限及原点,x增大时,y的值也增大;当k<0时,直线y=kx经过二,四象限及原点,x增大时,y的值反而减小。24 y = 2x 1224y随x的增大而增大y随x的增大而减小-3-6 一般地,正比例函数y=kx(k是常数,k≠0)的图象是一条经过原点的直线,我们称它为直线y=kx.当k >0时,直线y=kx经过第三、一象限及原点,从左向右上升,即随着x的增大y也增大;当k <0时,直线y=kx经过第二、四象限及原点,从左向右下降,即随着x的增大y反而减小. 1.函数y=-7x的图象在第 象限内,经过点(0, )与点(1, ),y随x的增大而 .二、四0-7减小 2、正比例函数y=(k+1)x的图像中y随x 的增大而增大,则k的取值范围是 。k> - 1 3.正比例函数y=(m-1)x的图象经过一、三象限,则m的取值范围是( )
A.m=1 B.m>1 C.m<1 D.m≥1B 4、若正比例函数y=(1-3m)x的图像经过点A(x1,y1)和B(x2,y2),当x1<x2时,y1 >y2,则m的取值范围是 。 5、直线y=(k2+3)x经过 象限,y随x的减小而 。一、三减小小结正比例函数1、定义: 一般地,形如 y=kx(k是常数,k≠0)的函数,叫做正比例函数,其中 k 叫做比例系数.2、图像过原点(0,0)和(1,k)的一条直线3、性质当k>0时,直线y=kx经过一、三象限及原点,y随 x增大而增大;当k<0时,直线y=kx经过二、四象限及原点,y 随x增大而减小。感悟:时间是一个“常量”,但对于勤奋者来说,却是一个“变量”,我们应该在有限的时间内做出伟大的事业!
你的收获与你的付出是成正比的,一份耕耘一份收获,相信自己,只要付出,你一定会有收获!1.一次函数的一般形式
y=kx+b (k,b是常数,k≠0)
正比例函数的一般形式
y=kx (k是常数,k≠0)
二者有什么联系?
正比例函数是一次函数b=0时的特殊情况
2.根据函数解析式画图,有哪几步?
列表描点连线旧知复习画出函数y= -2x+3的图象2+3
=50+3=3 - 2+3
=1 -4+3
= -1讨论交流一(1)对于自变量x的同一个值,一次函数y = -2x+3的函数值与函数y = -2x的函数值相比,有什么特点?
(2)说出点A(2,-1)到点B(2,2)是怎么平移的?
(口答)y= - 2xy= - 2x+3 观察上面两个函数图象的相同点与不同点,与同桌交流一下,谈谈自己的见解。讨论交流二(2分钟) 1、这两个函数的图象都是 ,并且它们的位置关系是 。
2、函数y=﹣2x的图象经过原点,函数y=-2x+3的图象与y轴交于点_______即它可以看作直线y=-2x向 平移 个单位长度而得到.直线平行上3(0,3) 直线y=-2x向下平移3个单位长度可得到函数 的图象观察图象中点的变化:y=-2x -3y=-2xy=-2x+3y=-2x-3一次函数y=kx+b的图象是 ,它可由正比例函数y=kx_____ 得到
当b>0时,直线向 平移∣b∣个单位长度
当b<0时,直线向 平移∣b∣个单位长度一条直线平移上下归纳小结: 1.将直线y=3x向下平移2个单位得到 直线_____________。 y=3x-2 2.将直线y=-x-5向上平移5个单位,得到直线____________。y =-x 3.函数y=kx-4的图像平行于直线y =-2x,则其函数的表达式为____________。y= -2x -4认识截距 1、请根据图像分别写出一次函数y = -2x+3与一次函数y=-2x -3的图像与y轴的交点坐标。 2、直线y =kx + b与y轴的交点坐标是什么?(0,b)合作时间一(两分钟) 请同桌之间互相给对方写一个一次函数的解析式,并指出对方所写一次函数的图像与y轴的交点坐标以及截距。 直线y=kx+b与y轴相交于点( 0,b ),b叫做直线y=kx+b在y轴上的截距,简称截距。 “截距”不是 “截得的距离”,它只是直线y=kx+b与y轴交点的纵坐标的值,如直线y=2x-7的截距是-7
注意:讨论交流三 1、在平面直角系中确定一条直线需要几个点? 2、画一次函数的图像你会找哪两个点?和你的同桌讨论,取哪两个点画图时比较方便? 3、你能直接利用函数解析式求函数图象与坐标轴交点的坐标吗?应用新知 例1:画出直线 并求出它的截距。解:对于 有截距:-2-2300(0, -2)(3,0) 同学们,本节课你学到了那些内容呢?请大家相互交流,总结所学的知识点。
1.一次函数y=kx+b的图像也是一条直线。
(画图像时,需考虑自变量的取值范围)
2.一次函数y=kx+b的图像可以通过平移正比例函数y=kx的图像得到。(两者图像之间的关系)
3.截距课堂小结:一.复习:
1.作函数图像的步骤是什么?(1)列表 (2)描点 (3)连线2.一次函数图像的特点是什么? 是一条直线,所以我们在作一次图像的时候只需要确定两个点,再过这两个点作直线就可以了。-6o-446246-2-2-4xy2y=0.5xy=xy=3xy=-2x(1)上面的函数都是什么函数?(2)正比例函数y=kx的
图象有什么特点?(3) y随x的增减性 ?经过的象限?(4)直线的倾斜程度 ? 正比例函数正比例函数y=kx的图象是经
过(0,0),(1,k)的一条直线k>0,过一、三象限及原点,
y随x的增大而增大;
k<0,过二、四象限及原点,
y随x的增大而减小; |k|越大,越接近y轴;| k |越小,越接近x轴y=-x 一次函数y=kx+b的图像是平行于直线y=kx的一条直线。所以,我们把一次函数y = kx +b的图像叫做直线y = kx +b 。
同时,一次函数y=kx+b的图像可由直线y=kx平移∣b∣个单位长度而得到(b>0,向上平移;b<0,向下平移)。复习回顾: 1、直线y=2x+5与直线y=-3x+5都经过y轴上的同一点( , )
2、直线y=2x -3,可以由直线y=2x +1经过
向 个单位而得到。直线 y=-3x可以由直线y=-3x -2 经过向 个单位而得到
3、已知直线y=kx+b平行于直线
且通过点(0,-3),求此函数的解析式。巩固训练0 5下平移4上平移2画出一次函数 的图象 01y-1.50x观察分析: 当一个点在直线上从左向右移动时,它的位置怎样变化 自变量x由___到___函数y的值从___到___大小小大y随x的增大而增大,
这时函数的图象从左到右上升; 的图象 观察分析: 自变量x由___到___函数y的值从___到___大小小大y随x的增大而减小,
这时函数的图象从左到右下降; y=-x+2 一次函数y=kx+b有下列性质:
?
(1) 当k>0时,y随x的增大而_____ ,这时函数的图象从左到右_____ ;
?
(2) 当k <0时, y随x的增大而_____,这时函数的图象从左到右_____. 概括减小下降增大上升六.探索发现(1) 在同一坐标系中作出下列函数的图象
(1)(2)(3)-3o-223123-1-1-2xy1思考:k、b的值跟图像的位置有什么关系?(2)在同一坐标系中作出下列函数的图象(1)(2)(3)-3o-223123-1-1-2xy1思考:k、b的值跟图像的位置有什么关系?结论k >ob=0b>0b<0b=0b>0b<0 通过作以上一次函数的图像我们发现y=kx+b
中,k,b的取值跟图像的关系如下:k <0一、三一、二、三一、三、四二、四一、二、四二、三、四当k >0时,y的值随x的增大而增大当k <0时,y的值随x的增大而减小根据图象确定k,b的取值K 0
b 0K 0
b 0K 0
b 0K 0
b 0K 0
b 0K 0
b 0K
b>
=<
=<
><
<>
<>
>
1 一次函数y=x-2的图象不经过的象限为( )
(A) 一 (B) 二 (C) 三 (D) 四
2 不经过第二象限的直线是 ( )
y=-2x+4 (B) y=2x-1
(C) y=2x+1 (D) y=-2x+1
3 若直线 y=kx+b经过一二四象限,那么直线 y=-bx+k经过 象限
4 直线 y=kx-k的图象的大致位置是 ( )
ABCDBB二、三、四C1.求出下列函数的解析式
(1)将直线y=5x向下平移6个单位;
(2)将直线 向上平移3个单位.
2.已知一次函数y=(1-2k)x+(2k+1)
(1)当k取何值时,y随x的增大而增大?
(2)当k取何值时,函数图象经过坐标系原点?
(3)当k取何值时,函数图象不经过第四象限?快马加鞭56结论一次函数的图象特征:
一次函数y=k x +b是经过(0,b)和( ,0)的一条直线一次函数y=kx+b性质:k>0时,y随x的增大而增大;
k<0时, y随x的增大而减小。直线y=kx+b是过点(0,b)且平行于直线y=kx的
一条直线正比例函数的图象特征:
是经过(0,0)和(1,k)两点的一条直线.
正比例函数的图象的性质:
(1)当k>0时,y随x的增大而增大;
(2)当k<0时,y随x的增大而减小.59结论:回味练习:
1、函数y=2x图象经过点(0, )与点(1, ),y随x的增大而 ;2、函数y=(a-2)x的图象经过第二、四象限,则a的范围是 ;
3、函数y=(1- k) x中y随x的增大而减小,则k的范围是 .02增大a<2k>14、直线y=-3x-6与x轴的交点坐标是 ,与y轴的交点坐标为 .(-2,0)(0,-6)5、直线y=3x-1经过 象限;
直线y=-2x+5经过 象限.
一、三、四一、二、四6、直线y=kx+b(k<0,b<0)经过 象限。
7、若直线y=kx+b经过一、二、四象限,则k 0,
b 0.
8、直线y=kx+b的图象如图所示,确定k、b符号:xx二、三、四<>K<0,b>0k>0,b<0
(1)已知直线y=kx+b平行于直线y=-2x+1,且过点(-2,4),分别求出k和b。
(2)一次函数y=4x-3和y=-4x-3的图象分别经过________象限和_______象限,它们的交点坐标是______.
(3)已知一次函数y=(2-m)x+m+2,那么
(a)当m为何值时,它的图象经过原点;
(b)当m为何值时,它的图象经过点(-1,5);
(c)当m为何值时,它的图象不经过第二象限。巩固练习:如何求一次函数的解析式例1、已知y与x成正比例,其图象过点( ,1),
求此函数的解析式。引申:
(1)、已知:y与x -1成正比例,且当x =-5时,y=3,求y与x之间的函数关系式。(2)、已知:y与z成正比例,z+1与x成正比例,且当x =1时,y=1;当x =0时,y=-3。
求y与x的函数关系式。(3)已知y与x成正比例,若y随x的增大而减小,且其图象经过(4,-a)和(a,-1)两点,求y与x之间的函数关系式。例2、已知:一次函数y=kx+b的图象经过点(5,-2)和(2,1)两点,求此一次函数的解析式。变式:已知y是x的一次函数,且其图象过点(5,-2)和(2,1),求其解析式。引申:
(1)已知:直线y=k x +b平行于直线y=2 x ,且经过点(-1,2),求y与x之间的函数关系式。(2)已知直线y=2x +b与两坐标轴围成的面积为4,求此函数的解析式。(3)已知一次函数的图象经过点(0,3),且与两坐标轴围成的面积为 ,求函数的解析式。
回味练习: 1.已知一次函数的图象经过点( 3 , 5 )和(-4,-9),求这个一次函数的解析式. 3.已知一次函数的图象经过点(-3 , 1)和(1,-5),求当x =5时,函数y的值. 4.若一次函数的图像与直线y =-3x+2交y轴与同一点,且过点(2,-6),求此一次函数的解析式. 2.已知直线y1=kx+b与直线y2 =-2x平行,且直线y1在y轴上的截距为2,求直线y1的解析式.例3、已知y=y1+y2,其中y1与x成正比例,y2与(x -2)成正比例,又当x=-1时,y=2;当x=2时,y=5. 求y与x的函数关系式。例4、根据图象,求出相应的函数关系式: 例5、已知一次函数的图象经过直线 y=-x+5与x轴的交点,且与y轴 的交点的纵坐标是-3,求函数的解析式。 例6、已知:点P是一次函数y=-2x+8的图象上一点,如果图象与x轴交于Q点,且△OPQ的面积等于6,求P点的坐标。回味练习:
1.函数y=2x-1与x轴交点坐标为_______ ,与y轴交点坐标为____,与两坐标轴围成的三角形面积是______.
2.若直线y=kx+b和直线y=-x平行,与y轴交点的纵坐标为-2,则直线的解析式为_______.
3.已知一次函数的图象经过点A(2,-1)
和点B,B是另一直线 与y轴的
交点,这个一次函数的解析式___________.( ,0)(0,-1)引申:
1.求直线y=2x+4与x轴、y轴 的交点坐标.
2.求直线y=2x-4与直线y=-x+1的交点坐标.
3.若直线y=ax-2与直线y=bx+1的图象交于x轴上同一点,则a:b=_____.
4. m为何值时,直线y=2x+m与 的交点横坐标为1.思考1:
若一次函数的图象交x轴于点A(- 6,0),交正比例函数的图象于点B,且点B在第二象限,它的横坐标为-4,又知:S△AOB=15,求直线AB的解析式。A(-6,0)(-4, ) By思考2:已知直线y=2x+m与两坐标轴围成的三角形面积为4,求m.变:已知直线y=kx+2与两坐标轴围成的 三角形面积为2,求k.
若过点(3,0)呢?若过点(2,1)呢? 1、小明从家里出发去菜地浇水,又去玉米地锄草,然后回家,其中x表示时间,y表示小明离他家的距离。 该图表示的函数是正比例函数吗?
是一次函数吗?你是怎样认为的? 2、小芳以200米/分钟的速度起跑后,先匀加速跑5分钟,每分钟提高速度20米/分,又匀速跑10分钟,请写出这段时间里她的跑步速度y(米/分钟)随跑步时间x(分钟)变化的函数关系式。 解:跑步的速度 y (米/分)随跑步时间 x (分钟)变化的函数关系式为: 上述函数,称为分段函数。y=20x+200y =300 3、为加强公民的节水意识,某城市制定了以下用水收费标准:每户每月用水未超过8立方米时,每立方米收取1元并加收0.3元的城市污水处理费;超过8立方米的部分每立方米收取1.5元并加收1.2元的城市污水处理费.设一户每月用水量为x立方米,应缴水费为y元,(1)给出y关于x的函数关系式;
(2)画出上述函数图象;
(8,10.4)●(3)该市一户某月若用水量为x=5立方米或x=10立方米时,求应缴水费;
(4)该市一户某月缴水费26.6元,求该户这月用水量. 自变量的不同取值范围内表示函数关系的解析式有不同的形式,这样的函数称为分段函数。归纳小结:巩固训练 1.某市出租车的计价方式为:开始3km内收费6元,以后每增加1km(不足1km,以1km计)加收1元。
(1)写出乘车路程xkm与收费y元的关系式;
(2)小明乘车5km,应付多少钱?7.6呢?
(3)小飞乘车付了15元,他至多乘车走了多远?
2.妈妈在用洗衣机洗涤衣服时,经历了进水、清洗、排水、脱水四个连续过程,其中进水、清洗、排水时洗衣机中的水量 y ( l )与时间 x (min)之间的关系如图所示,根据图象解答下列问题: ⑴你能根据图象获得哪些信息?(尽可能多的说出来)
⑵你能分别求出线段OA、AB、BC所表示的y与x之间的函数关系式吗?巩固训练挑战中考 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系. 根据图象进行以下探究:
(1)甲、乙两地之间的距离 为 km900(2)请解释图中B点的实际意义 图中B点的实际意义是:当慢车行驶4h时,慢车和快车相遇. 挑战中考 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系. 由图象可知,慢车12h行驶的路程为900km,所以慢车的速度为:(3)求慢车和快车的速度;900÷12=75(km/h) 当慢车行驶4h时,慢车和快车相遇,两车行驶的路程之和为900km,所以慢车和快车行驶的速度之和为:900÷4=225(km/h)挑战中考 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系. (4)求线段BC所表示的y与 x之间的函数关系式,并写出自变量的取值范围; 根据题意,快车行驶900km到达乙地,所以快车行驶900÷150=6(h)到达乙地,此时两车之间的距离为6×75=450(km),所以点C的坐标为(6,450).∴线段BC的函数关系式为y=225x-900 (4≤x≤6) 6×姚明的脚——你知道姚明的脚有多大吗? 姚明穿的鞋是56码,你能算出他的脚大约有多少厘米长吗? 鞋码与厘米转换表你如何算出姚明“56”码的脚有多少厘米?猜想函数关系:根据题意:解得得出函数关系:验证函数关系:x(cm)y(码)2m-10y=kx+by=2x -10 如图,多边形ABCDEF各角都为直角,动点P以 2cm/s 速度沿图甲的边框按B→C→D→E→F→A的路径移动,相应的△ABP的面积s关于时间t的函数图象如图乙.若AB=6cm,试回答下列问题: ostab6496cm2cm/s图甲图乙GHQ(7)M点坐标是否可以求出?N点坐标是否可以求出?
MN所在直线的函数关系式呢?ostab6496cm2cm/s(1)P点在整个的移动过程中△ABP的面积是怎样变化的?问题:(2)图甲中BC的长是多少?8cm(5)图乙中的a在图甲中具有什么实际意义?a的值是多少? 24(6)图乙中的b在图甲中具有什么实际意义?b的值是多少? (3)图甲中CD的长是多少?(4)图甲中DE的长是多少?4cm6cm42MN···图甲图乙小GHQ 如图,矩形ABCD中,AB=6cm,动点P以2cm/s速度沿图甲的边框按B→C→D→A的路径移动,相应的△ABP的面积s关于时间 t的函数图象如图乙.根据下图回答问题: 问题: (1)P点在整个的移动过程中△ABP的面积是怎样变化的? (3)图乙中的a在图甲中具有什么实际意义?a的值是多少? 10cm30(2)图甲中BC的长是多少?图甲图乙p 成功就是99%的汗水,加上1%的灵感。
------爱迪生 在科学上从没有平坦的大道,只有不畏艰险勇于攀登的人,才能达到光辉的顶点
马克思
