沪科版八年级上册13.3 一次函数与一次方程、一次不等式(共3课时)
文档属性
| 名称 | 沪科版八年级上册13.3 一次函数与一次方程、一次不等式(共3课时) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-14 00:00:00 | ||
图片预览










文档简介
课件31张PPT。 前面我们学习了一次函数.实际上一次函数是两个变量之间符合一定关系的一种互相对应、互相依存.它与我们七年级学过的一元一次方程、一元一次不等式、二元一次方程组有着必然的联系.这节课开始,我们就学着用函数的观点去看待方程(组)与不等式,并充分利用函数图象的直观性,形象地看待方程(组)、不等式的求解问题. 导语:老师为了检测小凯的数学学习情况,编了四道测试题.问题①:解方程2x+20=0问题②:当x为何值时,函数y=2x+20的值0?问题③:画出函数y=2x+20的图象,并确定
它与x轴的交点坐标;问题④:问题① ②有何关系? ① ③呢?x = -10当x = -10时,函数y=2x+20的值0.创设情景合作交流问题①:解方程2x+20=0问题②:当x为何值时,函数y=2x+20的值0?问题③:画出函数y=2x+20
的图象,并确定它 它 与x轴的交点坐标;问题④:问题① ②有何关系? ① ③呢?问题①与问题②可以看作是同一个问题两种形式.问题① ②是从数的角度看,问题③是从图形的角度看.直线y=2x+20与x轴的交点坐标为(-10,0)拓展1、方程ax+b=0(a、b为常数a≠0)的解是 .2、当x 时,一次函数y= ax+b( a≠0)的值0?3、直线y= ax+b 与x轴的交点坐标是 . 任何一个一元一次方程都可化为ax+b=0(a、b为常数a≠0)的形式,所以解这个方程从一次函数的角度可转化为“求一次函数y= ax+b( a≠0)的值为0时相应的自变量的值.” 从图象上看,这又相当于“求直线y= ax+b 与x轴的交点的横坐标”归
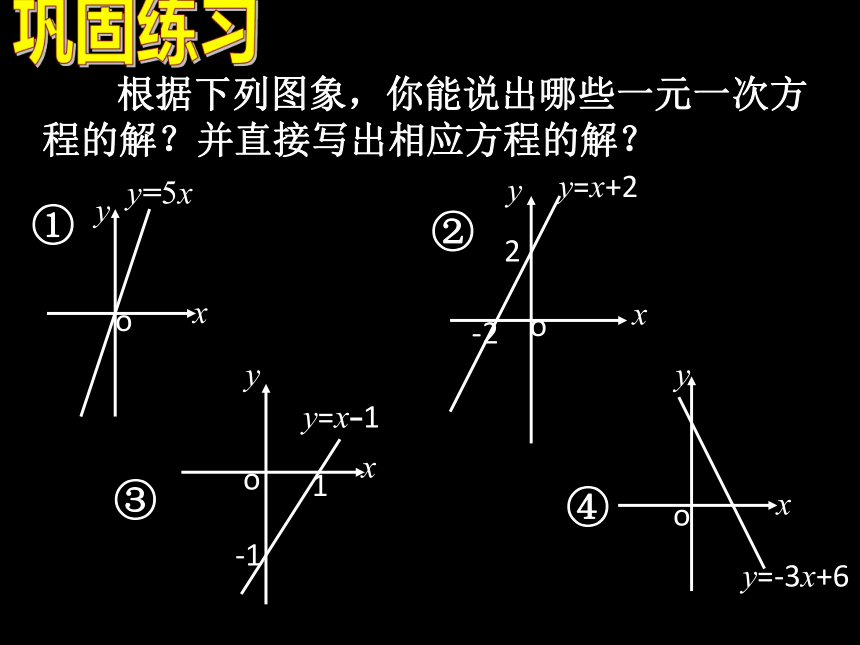
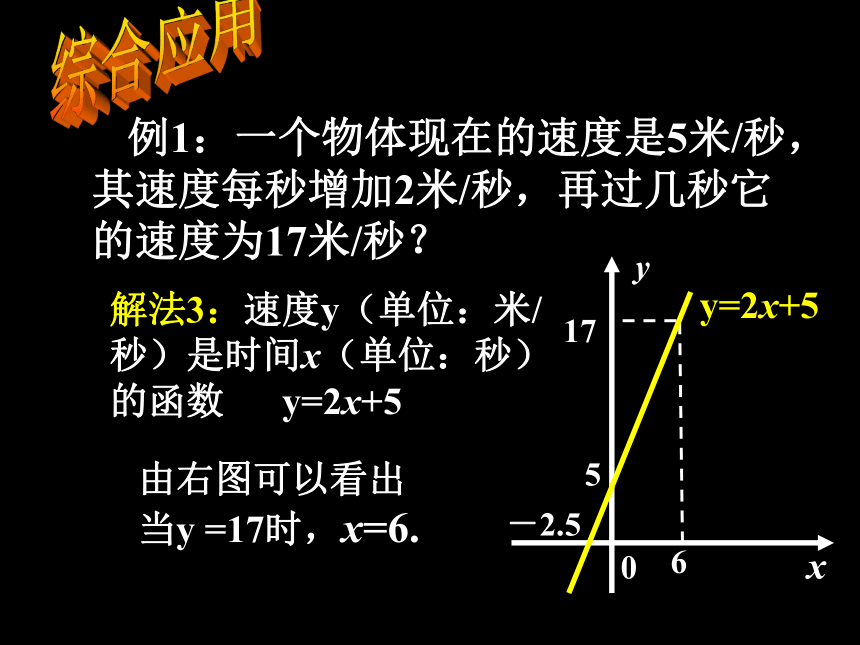
纳巩固练习 当x为何值时, y=8x-3的值为0?解方程 -7x+2=0解方程 ax+b=0当x为何值时, y=ax+b的值为0? 根据下列图象,你能说出哪些一元一次方程的解?并直接写出相应方程的解?巩固练习 综合应用 例1:一个物体现在的速度是5米/秒,其速度每秒增加2米/秒,再过几秒它的速度为17米/秒?解法1:设再过x秒它的速度为17米/秒.由题意得,2x+5=17解得 x=6答:再过6秒它的速度为17米/秒.综合应用 例1:一个物体现在的速度是5米/秒,其速度每秒增加2米/秒,再过几秒它的速度为17米/秒?解法2:速度y(单位:米/秒)是时间x(单位:秒)的函数 y=2x+5由2x+5=17 得 2x-12=0由右图看出直线y=2x-12与x轴的交点为(6,0),得x=6.综合应用 例1:一个物体现在的速度是5米/秒,其速度每秒增加2米/秒,再过几秒它的速度为17米/秒?解法3:速度y(单位:米/秒)是时间x(单位:秒)的函数 y=2x+5由右图可以看出当y =17时,x=6. 求ax+b=0(a≠0)的解x为何值时,y =ax+b的值为0?确定直线y =ax+b与x轴交点的横坐标 从形的角度看: 从数的角度看: 求ax +b=0(a≠0)的解总结反思施展才华1、直线y=x+3与x轴的交点坐标为 ,所以相应的方程x+3=0的解是 .x =-3(-3,0)x =-2③ ④ 我们可以把方程 6x ? 3 = x+2看作函数y= 6x ? 3与y=x+2在何时两函数值相等,即可从两个函数图象上看出,直线y =6x ? 3与y=x+2的交点,交点的横坐标即是方程的解.
例2:利用函数图象解出 x :6x ?3=x+2. 解法1:
将方程6x?3=x+2变形为5x?5=0,
画出函数 y =5x?5 的图象.Oxy1?5y=5x ?5 由图象可知直线 y =5x ? 5 与x 轴的交点为 (1,0) ,所以原方程的解为x =1 . 解法2:
由图象可以看出直线y=6x?3与y=x +2交于点(1,3),
∴方程的解为:x=10.5?21?323y=6x ?3 y=x +2 用不同种方法解下列方程:
① 2x ?3=x ?2.
② x + 3=2x +1.
巩固练习 (3)函数y=2x+6的图象与x轴交点横坐标与一元一次方程2x+6 =0的解有何关系? 一般地,一元一次方程kx+b=0的解就是一次函数y=kx+b的图象与x轴交点的横坐标.
问题1:已知一次函数y=2x+6 (1)画出函数图象,并求它与x轴交点的坐标; 温故知新oyy=2x+6xB(-3,0)A(0,6)(2)观察图象,判断当x取什么值时,函数值y=0?B(-3,0)x=-3 一元一次方程2x+6=0的解就是一次函数y=2x+6的图像与x轴交点的横坐标当y=0时当y>0时当y<0时 根据上面一次函数y=2x+6的图像,你能说出一元一次不等式2x+6>0和2x+6<0的解集吗? 分析:
当2 x +6<0,就是函数y=2 x +6中y<0,此时图像位于x轴下方,这部分图像所对应的自变量x的取值范围是x <-3,所以2 x +6<0的解集是x <-3;
合作探究x>-3x<-3当2x+6>0,就是函数y=2x+6中y>0,此时图像位于x轴上方,这部分图像所对应的自变量x的取值范围是x>-3,所以2x+6>0的解集是x>-3; 根据上面一次函数y=2x+6的图像,你能说出一元一次不等式2x+6>0和2x+6<0的解集吗?合作探究从图象上看,
2x+6>0的解集是直线y=2x+6位于x轴上方部分相应x的取值范围;x >-3x <-3 2x+6<0的解集是直线y=2x+6位于x轴下方部分相应x的取值范围.
你能说出一次函数y=kx+b与不等式kx+b>0,kx+b<0的关系吗?从图像上看,
(1)一元一次不等式kx+b>0的解集是直线y=kx+b位于x轴上方部分相应的x取值范围;
(2)一元一次不等式kx+b<0的解集是直线y=kx+b位于x轴下方部分相应的x取值范围.
归纳总结 1.一次函数y=-x+2的图像如图,你能说出不等式-x +2<0的解集吗?试一试x>2 2.一次函数y=kx+b的图像如图,你能说出不等式kx+b<0的解集吗?x<-46例1:画出函数y=-3x+6的图像,并结合图像回答: (1)求方程-3x+6=0的解? (2)求不等式-3x+6≥0的解集?
(1)画出函数y=-3x+6的图像,如图,图像与x轴交点的横坐标是2,所以,方程-3x+6=0的解就是x=2;
(2)观察图像可知,y≥0时,x的取值范围是x≤2,所以不等式-3x+6≥0的解集是 x≤2.应用举例2oy=-3x+6解:
6例2:利用图像求不等式-3x+6 ≤ 0的解集应用举例2oy=-3x+6解:
画出函数y=-3x+6的图像。小结:利用图像解不等式的步骤
1.画图;2.观察;3.结论 观察图像可知,y ≤ 0 时,x的取值范围是x ≥ 2,
所以不等式-3 x +6 ≤ 0的解集是x ≥ 2.
例3.利用图像求不等式-3x+6 ≤ 3的解集。解:
画出函数y=-3x+6的图像:
观察图像可知,y≤3时, x的取值范围是 x≥1,
所以不等式-3x+6≤3的解集是x≥1.思考讨论:xy20y=-3x+6361※1.已知函数y=4x-3.当x取何值时,函数的
图象在第四象限?
2.画出函数y=3x-6的图象,根据图象,指出:
(1) x取什么值时,函数值 y等于零?
(2) x取什么值时,函数值 y大于零?
(3) x取什么值时,函数值 y小于零?练一练3.画出函数y=-0.5x-1的图象,根据图象,求:
(1)函数图象与x轴的交点坐标;
(2)函数图象在x轴上方时,x的取值范围;
(3)函数图象在x轴下方时,x的取值范围.例4: 利用图象解不等式:
(1) 2x-5>-x+1,
(2) 2x-5<-x+1.解:设y1=2x-5,y2=-x+1,在坐标系中画出这两条直线,如图.两条直线的交点坐标是(2, -1) 。
(1)2x-5>-x+1的解集是y1>y2时
x的取值范围,为x>-2;
(2)2x-5<-x+1的解集是y1<y2时
x的取值范围,为x<-2.4、结合图象, 回答下列问题:
(1)当x取何值时,2x-5=-x+1?
(2)当x取何值时,2x-5>-x+1?
(3)当x取何值时,2x-5<-x+1?
例 某医药研究所研发了一种新药,在试验药效时发现,如果成人按规定计量服用,那么服药后每毫升血液中含药量y μg随时间x h的变化如图,当成人按规定计量服药后:
1)服药后多长时间血液中含药量最高,达每毫升多少微克?
2)分别求出x≤2和x≥2时,y与x之间的函数关系式;
3)如果每毫升血液中 含药量为4μg或4μg 以上时对治疗疾病是有效的,那么这个有效时间是多长?y1)服药后多长时间血液中含药量最高,达每毫升多少微克?
2)分别求出x≤2和x≥2时,y与x之间的函数关系式;
3)如果每毫升血液中含药量为4μg或4μg以上时对治疗疾病是有效的,那么这个有效时间是多长?y解:1)由图可知:服药后2分钟血液中含药量最高,达到每毫升6微克2)当x≤2时,设y=kx,因为图象经过(2,6)点,所以有
2k=6;k=3;即y=3x(x≤2)当x≥2时,设y=kx+b,因为图象经过(2,6),(10,3)点,所以有所以即y=- x+ (x≥2)3)将y=4代入y=3x得:3x=4, 即x=将y=4代入 ,得:
- x+ =4,即x=由图象可知,
有效时间t= - =6(小时)4y= - x+
它与x轴的交点坐标;问题④:问题① ②有何关系? ① ③呢?x = -10当x = -10时,函数y=2x+20的值0.创设情景合作交流问题①:解方程2x+20=0问题②:当x为何值时,函数y=2x+20的值0?问题③:画出函数y=2x+20
的图象,并确定它 它 与x轴的交点坐标;问题④:问题① ②有何关系? ① ③呢?问题①与问题②可以看作是同一个问题两种形式.问题① ②是从数的角度看,问题③是从图形的角度看.直线y=2x+20与x轴的交点坐标为(-10,0)拓展1、方程ax+b=0(a、b为常数a≠0)的解是 .2、当x 时,一次函数y= ax+b( a≠0)的值0?3、直线y= ax+b 与x轴的交点坐标是 . 任何一个一元一次方程都可化为ax+b=0(a、b为常数a≠0)的形式,所以解这个方程从一次函数的角度可转化为“求一次函数y= ax+b( a≠0)的值为0时相应的自变量的值.” 从图象上看,这又相当于“求直线y= ax+b 与x轴的交点的横坐标”归
纳巩固练习 当x为何值时, y=8x-3的值为0?解方程 -7x+2=0解方程 ax+b=0当x为何值时, y=ax+b的值为0? 根据下列图象,你能说出哪些一元一次方程的解?并直接写出相应方程的解?巩固练习 综合应用 例1:一个物体现在的速度是5米/秒,其速度每秒增加2米/秒,再过几秒它的速度为17米/秒?解法1:设再过x秒它的速度为17米/秒.由题意得,2x+5=17解得 x=6答:再过6秒它的速度为17米/秒.综合应用 例1:一个物体现在的速度是5米/秒,其速度每秒增加2米/秒,再过几秒它的速度为17米/秒?解法2:速度y(单位:米/秒)是时间x(单位:秒)的函数 y=2x+5由2x+5=17 得 2x-12=0由右图看出直线y=2x-12与x轴的交点为(6,0),得x=6.综合应用 例1:一个物体现在的速度是5米/秒,其速度每秒增加2米/秒,再过几秒它的速度为17米/秒?解法3:速度y(单位:米/秒)是时间x(单位:秒)的函数 y=2x+5由右图可以看出当y =17时,x=6. 求ax+b=0(a≠0)的解x为何值时,y =ax+b的值为0?确定直线y =ax+b与x轴交点的横坐标 从形的角度看: 从数的角度看: 求ax +b=0(a≠0)的解总结反思施展才华1、直线y=x+3与x轴的交点坐标为 ,所以相应的方程x+3=0的解是 .x =-3(-3,0)x =-2③ ④ 我们可以把方程 6x ? 3 = x+2看作函数y= 6x ? 3与y=x+2在何时两函数值相等,即可从两个函数图象上看出,直线y =6x ? 3与y=x+2的交点,交点的横坐标即是方程的解.
例2:利用函数图象解出 x :6x ?3=x+2. 解法1:
将方程6x?3=x+2变形为5x?5=0,
画出函数 y =5x?5 的图象.Oxy1?5y=5x ?5 由图象可知直线 y =5x ? 5 与x 轴的交点为 (1,0) ,所以原方程的解为x =1 . 解法2:
由图象可以看出直线y=6x?3与y=x +2交于点(1,3),
∴方程的解为:x=10.5?21?323y=6x ?3 y=x +2 用不同种方法解下列方程:
① 2x ?3=x ?2.
② x + 3=2x +1.
巩固练习 (3)函数y=2x+6的图象与x轴交点横坐标与一元一次方程2x+6 =0的解有何关系? 一般地,一元一次方程kx+b=0的解就是一次函数y=kx+b的图象与x轴交点的横坐标.
问题1:已知一次函数y=2x+6 (1)画出函数图象,并求它与x轴交点的坐标; 温故知新oyy=2x+6xB(-3,0)A(0,6)(2)观察图象,判断当x取什么值时,函数值y=0?B(-3,0)x=-3 一元一次方程2x+6=0的解就是一次函数y=2x+6的图像与x轴交点的横坐标当y=0时当y>0时当y<0时 根据上面一次函数y=2x+6的图像,你能说出一元一次不等式2x+6>0和2x+6<0的解集吗? 分析:
当2 x +6<0,就是函数y=2 x +6中y<0,此时图像位于x轴下方,这部分图像所对应的自变量x的取值范围是x <-3,所以2 x +6<0的解集是x <-3;
合作探究x>-3x<-3当2x+6>0,就是函数y=2x+6中y>0,此时图像位于x轴上方,这部分图像所对应的自变量x的取值范围是x>-3,所以2x+6>0的解集是x>-3; 根据上面一次函数y=2x+6的图像,你能说出一元一次不等式2x+6>0和2x+6<0的解集吗?合作探究从图象上看,
2x+6>0的解集是直线y=2x+6位于x轴上方部分相应x的取值范围;x >-3x <-3 2x+6<0的解集是直线y=2x+6位于x轴下方部分相应x的取值范围.
你能说出一次函数y=kx+b与不等式kx+b>0,kx+b<0的关系吗?从图像上看,
(1)一元一次不等式kx+b>0的解集是直线y=kx+b位于x轴上方部分相应的x取值范围;
(2)一元一次不等式kx+b<0的解集是直线y=kx+b位于x轴下方部分相应的x取值范围.
归纳总结 1.一次函数y=-x+2的图像如图,你能说出不等式-x +2<0的解集吗?试一试x>2 2.一次函数y=kx+b的图像如图,你能说出不等式kx+b<0的解集吗?x<-46例1:画出函数y=-3x+6的图像,并结合图像回答: (1)求方程-3x+6=0的解? (2)求不等式-3x+6≥0的解集?
(1)画出函数y=-3x+6的图像,如图,图像与x轴交点的横坐标是2,所以,方程-3x+6=0的解就是x=2;
(2)观察图像可知,y≥0时,x的取值范围是x≤2,所以不等式-3x+6≥0的解集是 x≤2.应用举例2oy=-3x+6解:
6例2:利用图像求不等式-3x+6 ≤ 0的解集应用举例2oy=-3x+6解:
画出函数y=-3x+6的图像。小结:利用图像解不等式的步骤
1.画图;2.观察;3.结论 观察图像可知,y ≤ 0 时,x的取值范围是x ≥ 2,
所以不等式-3 x +6 ≤ 0的解集是x ≥ 2.
例3.利用图像求不等式-3x+6 ≤ 3的解集。解:
画出函数y=-3x+6的图像:
观察图像可知,y≤3时, x的取值范围是 x≥1,
所以不等式-3x+6≤3的解集是x≥1.思考讨论:xy20y=-3x+6361※1.已知函数y=4x-3.当x取何值时,函数的
图象在第四象限?
2.画出函数y=3x-6的图象,根据图象,指出:
(1) x取什么值时,函数值 y等于零?
(2) x取什么值时,函数值 y大于零?
(3) x取什么值时,函数值 y小于零?练一练3.画出函数y=-0.5x-1的图象,根据图象,求:
(1)函数图象与x轴的交点坐标;
(2)函数图象在x轴上方时,x的取值范围;
(3)函数图象在x轴下方时,x的取值范围.例4: 利用图象解不等式:
(1) 2x-5>-x+1,
(2) 2x-5<-x+1.解:设y1=2x-5,y2=-x+1,在坐标系中画出这两条直线,如图.两条直线的交点坐标是(2, -1) 。
(1)2x-5>-x+1的解集是y1>y2时
x的取值范围,为x>-2;
(2)2x-5<-x+1的解集是y1<y2时
x的取值范围,为x<-2.4、结合图象, 回答下列问题:
(1)当x取何值时,2x-5=-x+1?
(2)当x取何值时,2x-5>-x+1?
(3)当x取何值时,2x-5<-x+1?
例 某医药研究所研发了一种新药,在试验药效时发现,如果成人按规定计量服用,那么服药后每毫升血液中含药量y μg随时间x h的变化如图,当成人按规定计量服药后:
1)服药后多长时间血液中含药量最高,达每毫升多少微克?
2)分别求出x≤2和x≥2时,y与x之间的函数关系式;
3)如果每毫升血液中 含药量为4μg或4μg 以上时对治疗疾病是有效的,那么这个有效时间是多长?y1)服药后多长时间血液中含药量最高,达每毫升多少微克?
2)分别求出x≤2和x≥2时,y与x之间的函数关系式;
3)如果每毫升血液中含药量为4μg或4μg以上时对治疗疾病是有效的,那么这个有效时间是多长?y解:1)由图可知:服药后2分钟血液中含药量最高,达到每毫升6微克2)当x≤2时,设y=kx,因为图象经过(2,6)点,所以有
2k=6;k=3;即y=3x(x≤2)当x≥2时,设y=kx+b,因为图象经过(2,6),(10,3)点,所以有所以即y=- x+ (x≥2)3)将y=4代入y=3x得:3x=4, 即x=将y=4代入 ,得:
- x+ =4,即x=由图象可知,
有效时间t= - =6(小时)4y= - x+
