2021-2022学年北师大版七年级数学下册1.4整式的乘法 同步练习(word版含解析)
文档属性
| 名称 | 2021-2022学年北师大版七年级数学下册1.4整式的乘法 同步练习(word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 85.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-17 00:00:00 | ||
图片预览




文档简介
2021-2022学年北师大版七年级数学下册《1-4整式的乘法》同步练习(附答案)
1.如图,用大小不同的9个长方形拼成一个大长方形ABCD,则图中阴影部分的面积是( )
A.ab+3a+b+3 B.ab+a+3b+3 C.ab+4a+b+4 D.ab+a+4b+4
2.计算(﹣2xy3)2 xy的结果是( )
A.﹣4x3y7 B.4x3y6 C.4x4y6 D.4x3y7
3.下列计算错误的是( )
A.(a3b) (ab2)=a4b3 B.(﹣mn3)2=m2n6
C.a8÷a4=a D.xy2﹣xy2=xy2
4.若(﹣2x2y3)m (xy)n=ax7y9,则常数a的值为( )
A.8 B.﹣8 C.4 D.﹣4
5.已知﹣2xmy2与4x2yn﹣1的积与﹣x4y3是同类项,求mn( )
A.2 B.3 C.4 D.5
6.若(x2+ax+1)(﹣6x3)的展开式中不含x4项,则a=( )
A.﹣6 B.0 C. D.﹣1
7.一个长方体的长、宽、高分别为2x、2x﹣1、x2,它的体积等于( )
A.4x4﹣4x2 B.4x4﹣2x3 C.4x3﹣2x2 D.4x4
8.若A(m2﹣3n)=m3﹣3mn,则代数式A的值为( )
A.m B.mn C.mn2 D.m2n
9.在一次数学课上,学习了单项式乘多项式,小刘回家后,拿出课堂笔记本复习,发现这样一道题:2x(﹣3x2﹣3x+1)=﹣6x3﹣□+2x,“□”的地方被墨水污染了,你认为“□”内应填写( )
A.﹣6x2 B.6x2 C.6x D.﹣6x
10.若(x﹣2)(x+3)=x2+ax+b,则a、b的值分别为( )
A.a=5,b=6 B.a=1,b=﹣6 C.a=1,b=6 D.a=5,b=﹣6
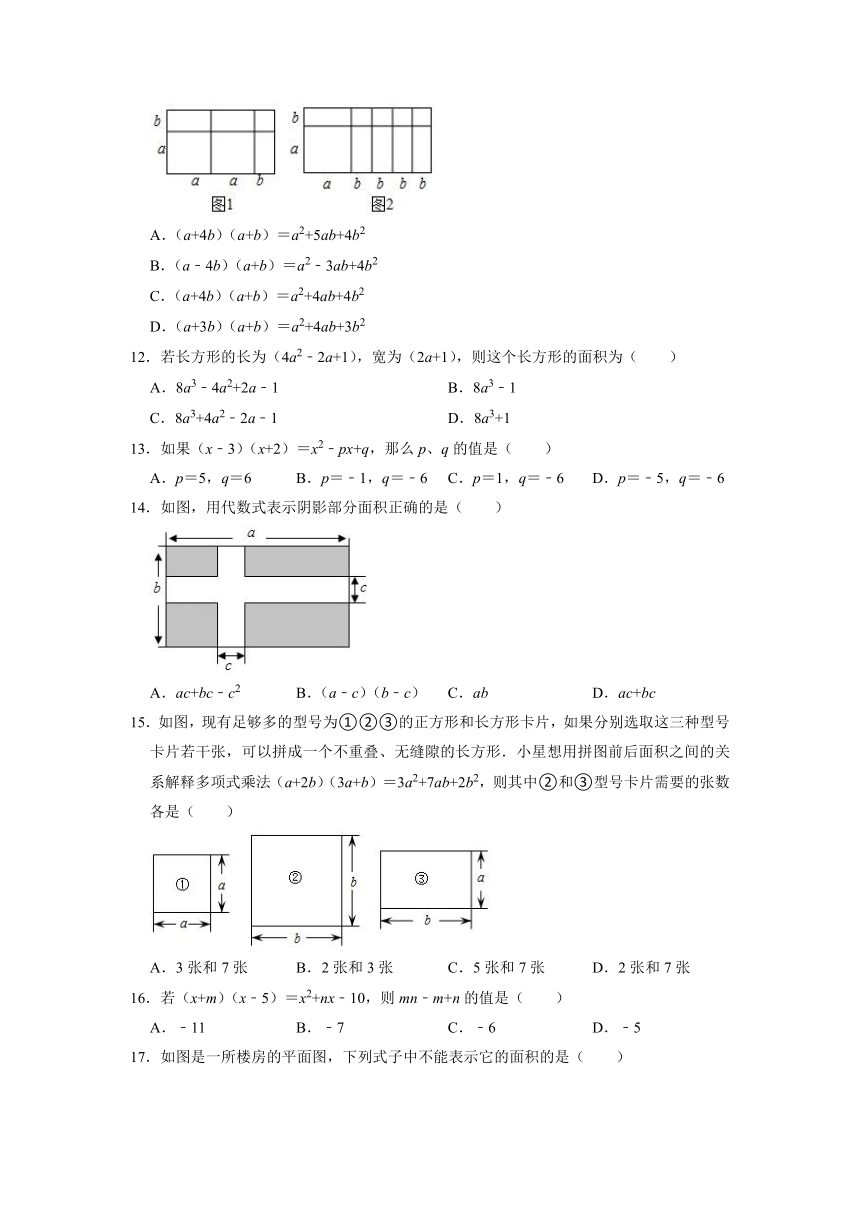
11.用图1的面积可以验证多项式的乘法运算(2a+b)(a+b)=2a2+3ab+b2,那么用图2的面积可以验证的乘法运算是( )
A.(a+4b)(a+b)=a2+5ab+4b2
B.(a﹣4b)(a+b)=a2﹣3ab+4b2
C.(a+4b)(a+b)=a2+4ab+4b2
D.(a+3b)(a+b)=a2+4ab+3b2
12.若长方形的长为(4a2﹣2a+1),宽为(2a+1),则这个长方形的面积为( )
A.8a3﹣4a2+2a﹣1 B.8a3﹣1
C.8a3+4a2﹣2a﹣1 D.8a3+1
13.如果(x﹣3)(x+2)=x2﹣px+q,那么p、q的值是( )
A.p=5,q=6 B.p=﹣1,q=﹣6 C.p=1,q=﹣6 D.p=﹣5,q=﹣6
14.如图,用代数式表示阴影部分面积正确的是( )
A.ac+bc﹣c2 B.(a﹣c)(b﹣c) C.ab D.ac+bc
15.如图,现有足够多的型号为①②③的正方形和长方形卡片,如果分别选取这三种型号卡片若干张,可以拼成一个不重叠、无缝隙的长方形.小星想用拼图前后面积之间的关系解释多项式乘法(a+2b)(3a+b)=3a2+7ab+2b2,则其中②和③型号卡片需要的张数各是( )
A.3张和7张 B.2张和3张 C.5张和7张 D.2张和7张
16.若(x+m)(x﹣5)=x2+nx﹣10,则mn﹣m+n的值是( )
A.﹣11 B.﹣7 C.﹣6 D.﹣5
17.如图是一所楼房的平面图,下列式子中不能表示它的面积的是( )
A.a2+5a+15 B.(a+5)(a+3)﹣3a
C.a(a+5)+15 D.a(a+3)+a2
18.如图,现有若干张卡片,分别是正方形卡片A、B和长方形卡片C,卡片大小如图所示.如果要拼一个长为(3a+b),宽为(a+3b)的大长方形,则需要C类卡片 张.
19.计算:(﹣2x3y) 5xy3= .
20.计算:(﹣2x)3 3x2= .
21.计算:(﹣3xy)3 (﹣x2z)= .
22.如果一个单项式乘以3x的积是3x2y,那么这个单项式是 .
23.如果am=2,bn=3,那么a3m b2n= .
24.计算:(﹣2a2)3 (﹣b3)2= .
25.若单项式﹣3x2ym+1与x3n﹣1y2是同类项,那么这两个单项式的积是 .
26.已知3x2y ★=6x3y,则“★”所表示的式子是 .
27.计算7x x2 (﹣x)3+5(x2)3的结果等于 .
28.已知a2n=4,b2n=9,则an bn的值为 .
29.计算:(﹣x) (6x2﹣3x+1)= .
30.计算:= .
31.计算:2a 3a2b= ,(﹣2x)3= ,3a(5a﹣2b)= .
32.已知x2+3x=﹣2,则代数式5+x(x+3)的值为 .
33.若a﹣b=3,3a+2b=5,则3a(a﹣b)+2b(a﹣b)= .
34.老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了一个多项式,形式如下:
×(﹣xy)=3x2y﹣xy2+xy,所捂多项式是 .
35.已知3ab A=6a2b﹣9ab2,则A= .
36.化简﹣m(3﹣m)+2(3﹣2m)= .
37.计算6x (3﹣2x)= ;(﹣0.5)2020×(﹣2)2021= .
38.若关于x的多项式(x+m)(2x﹣3)展开后不含x项,则m的值为 .
39.已知(x2+mx+n)(x﹣1)的结果中不含x2项和x项,则m= ,n= .
40.已知m+n=3,mn=﹣1,则(1﹣m)(1﹣n)的值为 .
41.计算:(x+3y)(2x﹣y)= .
42.整式乘除:
(1)(﹣2a2)(3ab2﹣5ab3);
(2)(x﹣1)(x2+x+1).
43.计算:
(1)××a3b2;
(2)(x﹣1)(2x+1)﹣2(x﹣5)(x+2).
44.计算:
(1)(2x2)3﹣x2 x4;
(2)(5x+2y)(x﹣3y).
45.如图1,在某住房小区的建设中,为了提高业主的宜居环境,小区准备在一个长为(4a+3b)米,宽为(2a+3b)米的长方形草坪上修建一横一竖,宽度均为b米的通道.
(1)通道的面积共有多少平方米?
(2)若修两横一竖,宽度均为b米的通道(如图2),已知a=2b,剩余草坪的面积是162平方米,求通道的宽度是多少米?
46.如图,哈市某小区有一块长为(2a+3b)米,宽为(2a﹣3b)米的长方形地块,角上有四个边长为(a﹣b)米的小正方形空地,开发商计划将阴影部分进行绿化.
(1)用含有a、b的式子表示绿化的总面积(结果写成最简形式).
(2)若a=20,b=10,绿化成本为50元/平方米,则完成绿化共需要多少元钱?
47.计算题
(1)(3ab2﹣2ab) ab.
(2)(x﹣2y)(x2﹣xy+4y2).
48.已知(x2+ax+4)(x2﹣2x+b)的乘积中不含x2和x3项,求a﹣2b的值.
参考答案
1.解:阴影面积:ab+3b+a+1×3=ab+3b+a+3;
故选:B.
2.解:(﹣2xy3)2 xy
=4x2y6 xy
=4x3y7.
故选:D.
3.解:A.(a3b) (ab2)=a4b3,故A正确;
B.(﹣mn3)2=m2n6,故B正确;
C.a8÷a4=a4,故C错误;
D.xy2﹣xy2=xy2,故D正确;
故选:C.
4.解:∵(﹣2x2y3)m (xy)n=ax7y9,
∴(﹣2)mx2my3m xnyn=ax7y9,
∴(﹣2)mx2m+ny3m+n=ax7y9,
∴,
解得:,
故(﹣2)m=4.
故选:C.
5.解:(﹣2xmy2) (4x2yn﹣1)=﹣8xm+2yn+1,
∵﹣2xmy2与4x2yn﹣1的积与﹣x4y3是同类项,
∴m+2=4,n+1=3,
解得:m=2,n=2,
∴mn=4.
故选:C.
6.解:(x2+ax+1)(﹣6x3)
=﹣6x5﹣6ax4﹣6x3,
∵不含x4,
∴﹣6a=0,
∴a=0,
故选:B.
7.解:由长方体的体积计算公式得,
2x(2x﹣1) x2=4x4﹣2x3,
故选:B.
8.解:∵A(m2﹣3n)=m3﹣3mn=m(m2﹣3n),
∴A=m.
故选:A.
9.解:∵2x(﹣3x2﹣3x+1)
=﹣6x3﹣6x2+2x=﹣6x3﹣□+2x,
∴“□”的地方被墨水污染的式子是:6x2.
故选:B.
10.解:∵(x﹣2)(x+3)=x2+x﹣6=x2+ax+b,
∴a=1,b=﹣6.
故选:B.
11.【答案】解:根据图2的面积得:(a+3b)(a+b)=a2+4ab+3b2,
故选:A.
12.解:由题意得:
(4a2﹣2a+1)(2a+1)
=8a3+4a2﹣4a2﹣2a+2a+1
=8a3+1,
故选:D.
13.解:(x﹣3)(x+2)=x2+2x﹣3x﹣6=x2﹣x﹣6,
∵(x﹣3)(x+2)=x2﹣px+q,
∴﹣p=﹣1,q=﹣6,
∴p=1.
故选:C.
14.解:由平移,可得,如图:
∴S阴影=(a﹣c)(b﹣c),
故选:B.
15.解:②型号卡片的面积为b2,③型号卡片的面积是ab,
∵(a+2b)(3a+b)=3a2+7ab+2b2,
∴需要②型号卡片2张,③型号卡片7张,
故选:D.
16.解:(x+m)(x﹣5)
=x2﹣5x+mx﹣5m
=x2+(m﹣5)x﹣5m,
∵(x+m)(x﹣5)=x2+nx﹣10,
∴m﹣5=n,5m=10,
∴m=2,n=﹣3,
∴mn﹣m+n=2×(﹣3)﹣2+(﹣3)=﹣6﹣2﹣3=﹣11.
故选:A.
17.解:A.是三个图形面积的和,正确,不符合题意;
B.是补成一个大长方形,用大长方形的面积减去补的长方形的面积,正确,不符合题意;
C.是上面大长方形的面积加上下面小长方形的面积,正确,不符合题意;
D.不是楼房的面积,错误,符合题意.
故选:D.
18.解:长为(3a+b),宽为(a+3b)的长方形的面积为:
(3a+b)(a+3b)=3a2+10ab+3b2,
∵A类卡片的面积为a2,B类卡片的面积为b2,C类卡片的面积为ab,
∴需要C类卡片10张;
故答案为:10.
19.解:(﹣2x3y) 5xy3=﹣10x4y4,
故答案为:﹣10x4y4.
20.解:(﹣2x)3 3x2=﹣8x3 3x2=﹣24x5,
故答案为:﹣24x5.
21.解:原式=﹣27x3y3 (﹣x2z)
=27x5y3z.
故答案为:27x5y3z.
22.解:∵一个单项式乘以3x的积是3x2y,
∴这个单项式是3x2y÷3x=xy.
故答案为:xy.
23.解:∵am=2,bn=3,
∴a3m b2n
=(am)3 (bn)2
=23×32
=8×9
=72.
故答案为:72.
24.解:原式=﹣8a6 b6
=﹣2a6b6,
故答案为:﹣2a6b6.
25.解:由题意得:3n﹣1=2,m+1=2.
∴m=1,n=1.
∴﹣3x2ym+1=﹣3x2y2,x3n﹣1y2=.
∴﹣3x2ym+1 x3n﹣1y2==.
故答案为:.
26.解:∵3x2y ★=6x3y,
∴“★”所表示的式子为:6x3y÷3x2y=2x,
故答案为:2x.
27.解:原式=7x3 (﹣x3)+5x6
=﹣7x3+3+5x6
=﹣7x6+5x6
=﹣2x6.
故答案为:﹣2x6.
28.解:∵a2n=4,b2n=9,
∴(an)2=4,(bn)2=9,
∴an=±2,bn=±3,
∴an bn的值为6或﹣6.
故答案为:6或﹣6.
29.解:(﹣x) (6x2﹣3x+1)
= 6x2 (﹣3x)×1
=﹣4x3+2x2﹣.
故答案为:﹣4x3+2x2﹣.
30.解:﹣ab(6ab﹣a+6b)
=﹣ab 6ab+ab a﹣ab 6b
=﹣4a2b2+a2b﹣4ab2.
故答案为:﹣4a2b2+a2b﹣4ab2.
31.解:2a 3a2b=6a3b;
(﹣2x)3=﹣8x3;
3a(5a﹣2b)=15a2﹣6ab.
故答案为:6a3b;﹣8x3;15a2﹣6ab.
32.解:原式=5+x2+3x,
∵x2+3x=﹣2,
∴原式=5﹣2=3,
故答案为:3.
33.解:∵a﹣b=3,3a+2b=5,
∴3a(a﹣b)+2b(a﹣b)
=(a﹣b)(3a+2b)
=3×5
=15.
故答案为:15.
34.解:∵(3x2y﹣xy2+xy)÷(﹣xy)=﹣6x+2y﹣1,
∴所捂多项式是﹣6x+2y﹣1,
故答案为:﹣6x+2y﹣1.
35.解:因为3ab A=6a2b﹣9ab2,
所以A=(6a2b﹣9ab2)÷3ab
=2a﹣3b.
故答案为:2a﹣3b.
36.解:﹣m(3﹣m)+2(3﹣2m)=﹣3m+m2+6﹣4m=m2﹣7m+6,
故答案为:m2﹣7m+6.
37.解:6x (3﹣2x)
=18x﹣12x2;
(﹣0.5)2020×(﹣2)2021
=﹣0.52020×22021
=﹣0.52020×22020×2
=﹣(0.5×2)2020×2
=﹣1×2
=﹣2.
故答案为:18x﹣12x2;﹣2.
38.解:原式=2x2+(2m﹣3)x﹣3m,
∵多项式展开后不含x项,
∴2m﹣3=0,
∴m=;
故答案为:.
39.解:(x2+mx+n)(x﹣1)=x3+(m﹣1)x2+(n﹣m)x﹣n.
∵结果中不含x2的项和x项,
∴m﹣1=0且n﹣m=0,
解得:m=1,n=1.
故答案为:1,1.
40.解:(1﹣m)(1﹣n)
=1﹣m﹣n+mn
=1﹣(m+n)+mn.
当m+n=3,mn=﹣1时,
原式=1﹣3﹣1
=﹣3.
故答案为:﹣3.
41.解:原式=x 2x﹣xy+3y 2x﹣3y y
=2x2﹣xy+6xy﹣3y2
=2x2+5xy﹣3y2.
故答案为:2x2+5xy﹣3y2.
42.解:(1)原式=﹣2a2 3ab2+2a2 5ab3
=﹣6a3b2+10a3b3;
(2)原式=x3+x2+x﹣x2﹣x﹣1
=x3﹣1.
43.解:(1)原式=﹣a6b3 a2b4 a3b2
=﹣a11b9;
(2)原式=2x2+x﹣2x﹣1﹣2(x2﹣3x﹣10)
=2x2+x﹣2x﹣1﹣2x2+6x+20
=5x+19.
44.解:(1)(2x2)3﹣x2 x4
=8x6﹣x6
=7x6;
(2)(5x+2y)(x﹣3y)
=5x2﹣15xy+2xy﹣6y2
=5x2﹣13xy﹣6y2.
45.解:(1)S通道=b(2a+3b)+b(4a+3b)﹣b2
=2ab+3b2+4ab+3b2﹣b2
=(6ab+5b2)平方米,
答:通道的面积共有(6ab+5b2)平方米;
(2)S草坪=(4a+3b)(2a+3b)﹣[2b(2a+3b)+b(4a+3b)﹣2b2]
=8a2+18ab+9b2﹣(4ab+6b2+4ab+3b2﹣2b2)
=8a2+18ab+9b2﹣8ab﹣7b2
=8a2+10ab+2b2,
∵a=2b,
∴8a2+10ab+2b2
=8×(2b)2+10×2b b+2b2
=32b2+20b2+2b2
=54b2
=162,
∴b2=3,
∴b=±(负值舍去)(米).
答:通道的宽度是米.
46.解:(1)题意得:
(2a+3b)(2a﹣3b)﹣4×(a﹣b)2
=4a2﹣9b2﹣4a2+8ab﹣4b2
=(﹣13b2+8ab)平方米.
答:绿化面积是(﹣13b2+8ab)平方米;
(2)当a=20,b=10时,
原式=﹣13×102+8×20×10
=﹣1300+1600
=300(平方米),
300×50=15000(元),
答:完成绿化共需要15000元钱.
47.解:(1)(3ab2﹣2ab) ab=3a2b3﹣2a2b2.
(2)(x﹣2y)(x2﹣xy+4y2)
=x3﹣x2y+4xy2﹣2x2y+2xy2﹣8y3
=x3﹣3x2y+6xy2﹣8y3.
48.解:原式=x4﹣2x3+bx2+ax3﹣2ax2+abx+4x2﹣8x+4b
=x4+(a﹣2)x3+(b﹣2a+4)x2+(ab﹣8)x+4b,
∵其结果中不含x2和x3项,
∴a﹣2=0,b﹣2a+4=0,
解得:a=2,b=0,
∴a﹣2b=2﹣2×0=2.
答:a﹣2b的值为2.
1.如图,用大小不同的9个长方形拼成一个大长方形ABCD,则图中阴影部分的面积是( )
A.ab+3a+b+3 B.ab+a+3b+3 C.ab+4a+b+4 D.ab+a+4b+4
2.计算(﹣2xy3)2 xy的结果是( )
A.﹣4x3y7 B.4x3y6 C.4x4y6 D.4x3y7
3.下列计算错误的是( )
A.(a3b) (ab2)=a4b3 B.(﹣mn3)2=m2n6
C.a8÷a4=a D.xy2﹣xy2=xy2
4.若(﹣2x2y3)m (xy)n=ax7y9,则常数a的值为( )
A.8 B.﹣8 C.4 D.﹣4
5.已知﹣2xmy2与4x2yn﹣1的积与﹣x4y3是同类项,求mn( )
A.2 B.3 C.4 D.5
6.若(x2+ax+1)(﹣6x3)的展开式中不含x4项,则a=( )
A.﹣6 B.0 C. D.﹣1
7.一个长方体的长、宽、高分别为2x、2x﹣1、x2,它的体积等于( )
A.4x4﹣4x2 B.4x4﹣2x3 C.4x3﹣2x2 D.4x4
8.若A(m2﹣3n)=m3﹣3mn,则代数式A的值为( )
A.m B.mn C.mn2 D.m2n
9.在一次数学课上,学习了单项式乘多项式,小刘回家后,拿出课堂笔记本复习,发现这样一道题:2x(﹣3x2﹣3x+1)=﹣6x3﹣□+2x,“□”的地方被墨水污染了,你认为“□”内应填写( )
A.﹣6x2 B.6x2 C.6x D.﹣6x
10.若(x﹣2)(x+3)=x2+ax+b,则a、b的值分别为( )
A.a=5,b=6 B.a=1,b=﹣6 C.a=1,b=6 D.a=5,b=﹣6
11.用图1的面积可以验证多项式的乘法运算(2a+b)(a+b)=2a2+3ab+b2,那么用图2的面积可以验证的乘法运算是( )
A.(a+4b)(a+b)=a2+5ab+4b2
B.(a﹣4b)(a+b)=a2﹣3ab+4b2
C.(a+4b)(a+b)=a2+4ab+4b2
D.(a+3b)(a+b)=a2+4ab+3b2
12.若长方形的长为(4a2﹣2a+1),宽为(2a+1),则这个长方形的面积为( )
A.8a3﹣4a2+2a﹣1 B.8a3﹣1
C.8a3+4a2﹣2a﹣1 D.8a3+1
13.如果(x﹣3)(x+2)=x2﹣px+q,那么p、q的值是( )
A.p=5,q=6 B.p=﹣1,q=﹣6 C.p=1,q=﹣6 D.p=﹣5,q=﹣6
14.如图,用代数式表示阴影部分面积正确的是( )
A.ac+bc﹣c2 B.(a﹣c)(b﹣c) C.ab D.ac+bc
15.如图,现有足够多的型号为①②③的正方形和长方形卡片,如果分别选取这三种型号卡片若干张,可以拼成一个不重叠、无缝隙的长方形.小星想用拼图前后面积之间的关系解释多项式乘法(a+2b)(3a+b)=3a2+7ab+2b2,则其中②和③型号卡片需要的张数各是( )
A.3张和7张 B.2张和3张 C.5张和7张 D.2张和7张
16.若(x+m)(x﹣5)=x2+nx﹣10,则mn﹣m+n的值是( )
A.﹣11 B.﹣7 C.﹣6 D.﹣5
17.如图是一所楼房的平面图,下列式子中不能表示它的面积的是( )
A.a2+5a+15 B.(a+5)(a+3)﹣3a
C.a(a+5)+15 D.a(a+3)+a2
18.如图,现有若干张卡片,分别是正方形卡片A、B和长方形卡片C,卡片大小如图所示.如果要拼一个长为(3a+b),宽为(a+3b)的大长方形,则需要C类卡片 张.
19.计算:(﹣2x3y) 5xy3= .
20.计算:(﹣2x)3 3x2= .
21.计算:(﹣3xy)3 (﹣x2z)= .
22.如果一个单项式乘以3x的积是3x2y,那么这个单项式是 .
23.如果am=2,bn=3,那么a3m b2n= .
24.计算:(﹣2a2)3 (﹣b3)2= .
25.若单项式﹣3x2ym+1与x3n﹣1y2是同类项,那么这两个单项式的积是 .
26.已知3x2y ★=6x3y,则“★”所表示的式子是 .
27.计算7x x2 (﹣x)3+5(x2)3的结果等于 .
28.已知a2n=4,b2n=9,则an bn的值为 .
29.计算:(﹣x) (6x2﹣3x+1)= .
30.计算:= .
31.计算:2a 3a2b= ,(﹣2x)3= ,3a(5a﹣2b)= .
32.已知x2+3x=﹣2,则代数式5+x(x+3)的值为 .
33.若a﹣b=3,3a+2b=5,则3a(a﹣b)+2b(a﹣b)= .
34.老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了一个多项式,形式如下:
×(﹣xy)=3x2y﹣xy2+xy,所捂多项式是 .
35.已知3ab A=6a2b﹣9ab2,则A= .
36.化简﹣m(3﹣m)+2(3﹣2m)= .
37.计算6x (3﹣2x)= ;(﹣0.5)2020×(﹣2)2021= .
38.若关于x的多项式(x+m)(2x﹣3)展开后不含x项,则m的值为 .
39.已知(x2+mx+n)(x﹣1)的结果中不含x2项和x项,则m= ,n= .
40.已知m+n=3,mn=﹣1,则(1﹣m)(1﹣n)的值为 .
41.计算:(x+3y)(2x﹣y)= .
42.整式乘除:
(1)(﹣2a2)(3ab2﹣5ab3);
(2)(x﹣1)(x2+x+1).
43.计算:
(1)××a3b2;
(2)(x﹣1)(2x+1)﹣2(x﹣5)(x+2).
44.计算:
(1)(2x2)3﹣x2 x4;
(2)(5x+2y)(x﹣3y).
45.如图1,在某住房小区的建设中,为了提高业主的宜居环境,小区准备在一个长为(4a+3b)米,宽为(2a+3b)米的长方形草坪上修建一横一竖,宽度均为b米的通道.
(1)通道的面积共有多少平方米?
(2)若修两横一竖,宽度均为b米的通道(如图2),已知a=2b,剩余草坪的面积是162平方米,求通道的宽度是多少米?
46.如图,哈市某小区有一块长为(2a+3b)米,宽为(2a﹣3b)米的长方形地块,角上有四个边长为(a﹣b)米的小正方形空地,开发商计划将阴影部分进行绿化.
(1)用含有a、b的式子表示绿化的总面积(结果写成最简形式).
(2)若a=20,b=10,绿化成本为50元/平方米,则完成绿化共需要多少元钱?
47.计算题
(1)(3ab2﹣2ab) ab.
(2)(x﹣2y)(x2﹣xy+4y2).
48.已知(x2+ax+4)(x2﹣2x+b)的乘积中不含x2和x3项,求a﹣2b的值.
参考答案
1.解:阴影面积:ab+3b+a+1×3=ab+3b+a+3;
故选:B.
2.解:(﹣2xy3)2 xy
=4x2y6 xy
=4x3y7.
故选:D.
3.解:A.(a3b) (ab2)=a4b3,故A正确;
B.(﹣mn3)2=m2n6,故B正确;
C.a8÷a4=a4,故C错误;
D.xy2﹣xy2=xy2,故D正确;
故选:C.
4.解:∵(﹣2x2y3)m (xy)n=ax7y9,
∴(﹣2)mx2my3m xnyn=ax7y9,
∴(﹣2)mx2m+ny3m+n=ax7y9,
∴,
解得:,
故(﹣2)m=4.
故选:C.
5.解:(﹣2xmy2) (4x2yn﹣1)=﹣8xm+2yn+1,
∵﹣2xmy2与4x2yn﹣1的积与﹣x4y3是同类项,
∴m+2=4,n+1=3,
解得:m=2,n=2,
∴mn=4.
故选:C.
6.解:(x2+ax+1)(﹣6x3)
=﹣6x5﹣6ax4﹣6x3,
∵不含x4,
∴﹣6a=0,
∴a=0,
故选:B.
7.解:由长方体的体积计算公式得,
2x(2x﹣1) x2=4x4﹣2x3,
故选:B.
8.解:∵A(m2﹣3n)=m3﹣3mn=m(m2﹣3n),
∴A=m.
故选:A.
9.解:∵2x(﹣3x2﹣3x+1)
=﹣6x3﹣6x2+2x=﹣6x3﹣□+2x,
∴“□”的地方被墨水污染的式子是:6x2.
故选:B.
10.解:∵(x﹣2)(x+3)=x2+x﹣6=x2+ax+b,
∴a=1,b=﹣6.
故选:B.
11.【答案】解:根据图2的面积得:(a+3b)(a+b)=a2+4ab+3b2,
故选:A.
12.解:由题意得:
(4a2﹣2a+1)(2a+1)
=8a3+4a2﹣4a2﹣2a+2a+1
=8a3+1,
故选:D.
13.解:(x﹣3)(x+2)=x2+2x﹣3x﹣6=x2﹣x﹣6,
∵(x﹣3)(x+2)=x2﹣px+q,
∴﹣p=﹣1,q=﹣6,
∴p=1.
故选:C.
14.解:由平移,可得,如图:
∴S阴影=(a﹣c)(b﹣c),
故选:B.
15.解:②型号卡片的面积为b2,③型号卡片的面积是ab,
∵(a+2b)(3a+b)=3a2+7ab+2b2,
∴需要②型号卡片2张,③型号卡片7张,
故选:D.
16.解:(x+m)(x﹣5)
=x2﹣5x+mx﹣5m
=x2+(m﹣5)x﹣5m,
∵(x+m)(x﹣5)=x2+nx﹣10,
∴m﹣5=n,5m=10,
∴m=2,n=﹣3,
∴mn﹣m+n=2×(﹣3)﹣2+(﹣3)=﹣6﹣2﹣3=﹣11.
故选:A.
17.解:A.是三个图形面积的和,正确,不符合题意;
B.是补成一个大长方形,用大长方形的面积减去补的长方形的面积,正确,不符合题意;
C.是上面大长方形的面积加上下面小长方形的面积,正确,不符合题意;
D.不是楼房的面积,错误,符合题意.
故选:D.
18.解:长为(3a+b),宽为(a+3b)的长方形的面积为:
(3a+b)(a+3b)=3a2+10ab+3b2,
∵A类卡片的面积为a2,B类卡片的面积为b2,C类卡片的面积为ab,
∴需要C类卡片10张;
故答案为:10.
19.解:(﹣2x3y) 5xy3=﹣10x4y4,
故答案为:﹣10x4y4.
20.解:(﹣2x)3 3x2=﹣8x3 3x2=﹣24x5,
故答案为:﹣24x5.
21.解:原式=﹣27x3y3 (﹣x2z)
=27x5y3z.
故答案为:27x5y3z.
22.解:∵一个单项式乘以3x的积是3x2y,
∴这个单项式是3x2y÷3x=xy.
故答案为:xy.
23.解:∵am=2,bn=3,
∴a3m b2n
=(am)3 (bn)2
=23×32
=8×9
=72.
故答案为:72.
24.解:原式=﹣8a6 b6
=﹣2a6b6,
故答案为:﹣2a6b6.
25.解:由题意得:3n﹣1=2,m+1=2.
∴m=1,n=1.
∴﹣3x2ym+1=﹣3x2y2,x3n﹣1y2=.
∴﹣3x2ym+1 x3n﹣1y2==.
故答案为:.
26.解:∵3x2y ★=6x3y,
∴“★”所表示的式子为:6x3y÷3x2y=2x,
故答案为:2x.
27.解:原式=7x3 (﹣x3)+5x6
=﹣7x3+3+5x6
=﹣7x6+5x6
=﹣2x6.
故答案为:﹣2x6.
28.解:∵a2n=4,b2n=9,
∴(an)2=4,(bn)2=9,
∴an=±2,bn=±3,
∴an bn的值为6或﹣6.
故答案为:6或﹣6.
29.解:(﹣x) (6x2﹣3x+1)
= 6x2 (﹣3x)×1
=﹣4x3+2x2﹣.
故答案为:﹣4x3+2x2﹣.
30.解:﹣ab(6ab﹣a+6b)
=﹣ab 6ab+ab a﹣ab 6b
=﹣4a2b2+a2b﹣4ab2.
故答案为:﹣4a2b2+a2b﹣4ab2.
31.解:2a 3a2b=6a3b;
(﹣2x)3=﹣8x3;
3a(5a﹣2b)=15a2﹣6ab.
故答案为:6a3b;﹣8x3;15a2﹣6ab.
32.解:原式=5+x2+3x,
∵x2+3x=﹣2,
∴原式=5﹣2=3,
故答案为:3.
33.解:∵a﹣b=3,3a+2b=5,
∴3a(a﹣b)+2b(a﹣b)
=(a﹣b)(3a+2b)
=3×5
=15.
故答案为:15.
34.解:∵(3x2y﹣xy2+xy)÷(﹣xy)=﹣6x+2y﹣1,
∴所捂多项式是﹣6x+2y﹣1,
故答案为:﹣6x+2y﹣1.
35.解:因为3ab A=6a2b﹣9ab2,
所以A=(6a2b﹣9ab2)÷3ab
=2a﹣3b.
故答案为:2a﹣3b.
36.解:﹣m(3﹣m)+2(3﹣2m)=﹣3m+m2+6﹣4m=m2﹣7m+6,
故答案为:m2﹣7m+6.
37.解:6x (3﹣2x)
=18x﹣12x2;
(﹣0.5)2020×(﹣2)2021
=﹣0.52020×22021
=﹣0.52020×22020×2
=﹣(0.5×2)2020×2
=﹣1×2
=﹣2.
故答案为:18x﹣12x2;﹣2.
38.解:原式=2x2+(2m﹣3)x﹣3m,
∵多项式展开后不含x项,
∴2m﹣3=0,
∴m=;
故答案为:.
39.解:(x2+mx+n)(x﹣1)=x3+(m﹣1)x2+(n﹣m)x﹣n.
∵结果中不含x2的项和x项,
∴m﹣1=0且n﹣m=0,
解得:m=1,n=1.
故答案为:1,1.
40.解:(1﹣m)(1﹣n)
=1﹣m﹣n+mn
=1﹣(m+n)+mn.
当m+n=3,mn=﹣1时,
原式=1﹣3﹣1
=﹣3.
故答案为:﹣3.
41.解:原式=x 2x﹣xy+3y 2x﹣3y y
=2x2﹣xy+6xy﹣3y2
=2x2+5xy﹣3y2.
故答案为:2x2+5xy﹣3y2.
42.解:(1)原式=﹣2a2 3ab2+2a2 5ab3
=﹣6a3b2+10a3b3;
(2)原式=x3+x2+x﹣x2﹣x﹣1
=x3﹣1.
43.解:(1)原式=﹣a6b3 a2b4 a3b2
=﹣a11b9;
(2)原式=2x2+x﹣2x﹣1﹣2(x2﹣3x﹣10)
=2x2+x﹣2x﹣1﹣2x2+6x+20
=5x+19.
44.解:(1)(2x2)3﹣x2 x4
=8x6﹣x6
=7x6;
(2)(5x+2y)(x﹣3y)
=5x2﹣15xy+2xy﹣6y2
=5x2﹣13xy﹣6y2.
45.解:(1)S通道=b(2a+3b)+b(4a+3b)﹣b2
=2ab+3b2+4ab+3b2﹣b2
=(6ab+5b2)平方米,
答:通道的面积共有(6ab+5b2)平方米;
(2)S草坪=(4a+3b)(2a+3b)﹣[2b(2a+3b)+b(4a+3b)﹣2b2]
=8a2+18ab+9b2﹣(4ab+6b2+4ab+3b2﹣2b2)
=8a2+18ab+9b2﹣8ab﹣7b2
=8a2+10ab+2b2,
∵a=2b,
∴8a2+10ab+2b2
=8×(2b)2+10×2b b+2b2
=32b2+20b2+2b2
=54b2
=162,
∴b2=3,
∴b=±(负值舍去)(米).
答:通道的宽度是米.
46.解:(1)题意得:
(2a+3b)(2a﹣3b)﹣4×(a﹣b)2
=4a2﹣9b2﹣4a2+8ab﹣4b2
=(﹣13b2+8ab)平方米.
答:绿化面积是(﹣13b2+8ab)平方米;
(2)当a=20,b=10时,
原式=﹣13×102+8×20×10
=﹣1300+1600
=300(平方米),
300×50=15000(元),
答:完成绿化共需要15000元钱.
47.解:(1)(3ab2﹣2ab) ab=3a2b3﹣2a2b2.
(2)(x﹣2y)(x2﹣xy+4y2)
=x3﹣x2y+4xy2﹣2x2y+2xy2﹣8y3
=x3﹣3x2y+6xy2﹣8y3.
48.解:原式=x4﹣2x3+bx2+ax3﹣2ax2+abx+4x2﹣8x+4b
=x4+(a﹣2)x3+(b﹣2a+4)x2+(ab﹣8)x+4b,
∵其结果中不含x2和x3项,
∴a﹣2=0,b﹣2a+4=0,
解得:a=2,b=0,
∴a﹣2b=2﹣2×0=2.
答:a﹣2b的值为2.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
