2021-2022学年北师大版七年级数学下册1.5平方差公式 同步练习(word版含解析)
文档属性
| 名称 | 2021-2022学年北师大版七年级数学下册1.5平方差公式 同步练习(word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 65.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-17 09:37:50 | ||
图片预览



文档简介
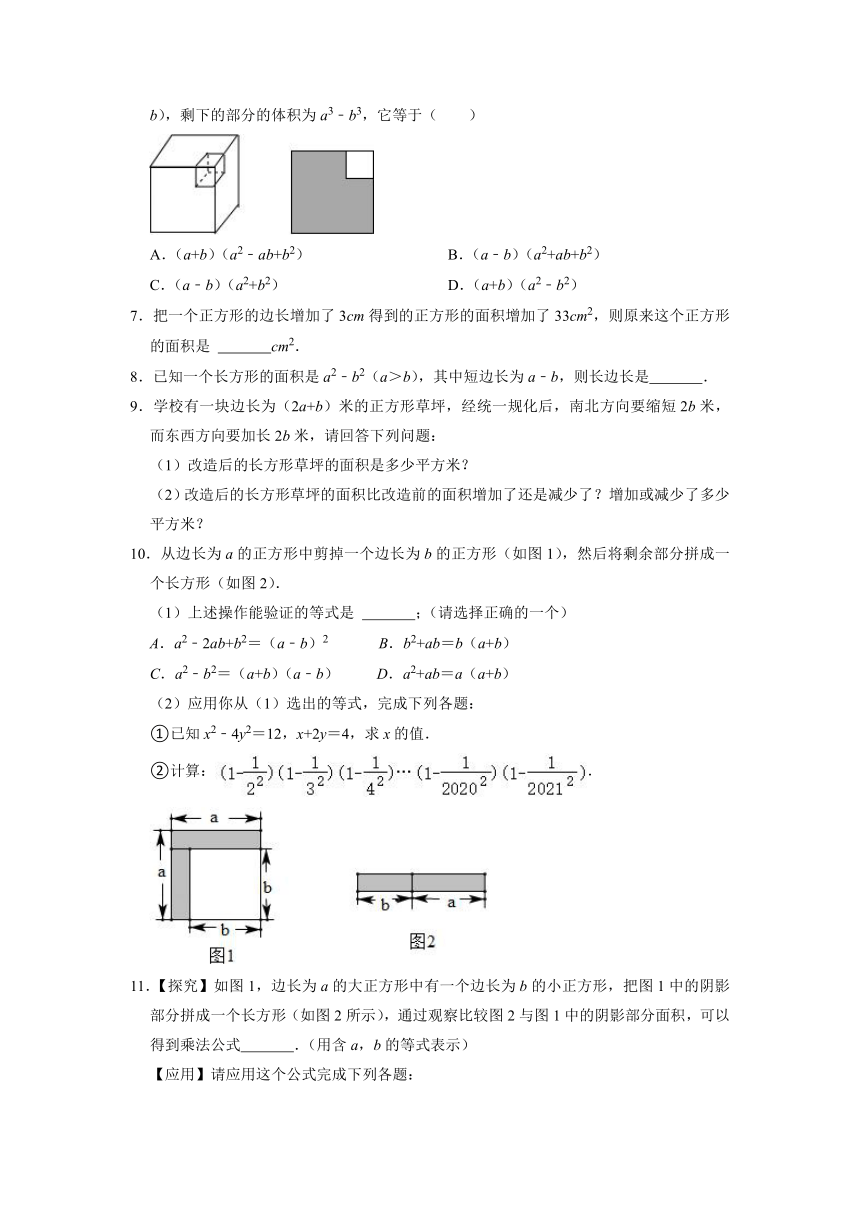
2021-2022学年北师大版七年级数学下册《1-5平方差公式》同步练习(附答案)
1.某厂原来生产一种边长为a厘米的正方形地砖,现将地砖的一边扩大3厘米,另一边缩短3厘米,改成生产长方形地砖.若材料的成本价为每平方厘米b元,则这种长方形地砖每块的材料成本价与正方形地砖相比( )
A.增加了9b元 B.增加了3ab元
C.减少了9b元 D.减少了3ab元
2.为了美化城市,经统一规划,将一正方形草坪的南北方向增加3m,东西方向缩短3m,则改造后的长方形草坪面积与原来正方形草坪面积相比( )
A.保持不变 B.增加9m2 C.增加6m2 D.减少9m2
3.如图,边长为m+3的正方形纸片剪去一个边长为m的正方形后,用剩余部分剪拼成一个长方形(不重叠无缝隙).若拼成的长方形一边长为3,则另一边长为( )
A.2m+3 B.2m+6 C.m+3 D.m+6
4.一个矩形的长为(a+b)m,宽为(a﹣b)m,则这个矩形的面积为( )
A.(a2﹣b2)m2 B.(a+b)2m2 C.(a﹣b)2m2 D.(2a﹣2b)m2
5.如图(1),在边长为a的大正方形中,剪去一个边长为b的小正方形(a>b),然后将余下的部分剪开拼成长方形,如图(2),若大正方形的周长为c1,长方形的周长为c2,则c1与c2的大小关系是( )
A.c1>c2 B.c1=c2 C.c1<c2 D.不能确定
6.如图所示,在边长为a的正方形中减去一个边长为b的小正方形(a>b),剩下的部分的面积,可得到平方差公式;那么在边长a的正方体中减去一个边长为b的小正方体(a>b),剩下的部分的体积为a3﹣b3,它等于( )
A.(a+b)(a2﹣ab+b2) B.(a﹣b)(a2+ab+b2)
C.(a﹣b)(a2+b2) D.(a+b)(a2﹣b2)
7.把一个正方形的边长增加了3cm得到的正方形的面积增加了33cm2,则原来这个正方形的面积是 cm2.
8.已知一个长方形的面积是a2﹣b2(a>b),其中短边长为a﹣b,则长边长是 .
9.学校有一块边长为(2a+b)米的正方形草坪,经统一规化后,南北方向要缩短2b米,而东西方向要加长2b米,请回答下列问题:
(1)改造后的长方形草坪的面积是多少平方米?
(2)改造后的长方形草坪的面积比改造前的面积增加了还是减少了?增加或减少了多少平方米?
10.从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)上述操作能验证的等式是 ;(请选择正确的一个)
A.a2﹣2ab+b2=(a﹣b)2 B.b2+ab=b(a+b)
C.a2﹣b2=(a+b)(a﹣b) D.a2+ab=a(a+b)
(2)应用你从(1)选出的等式,完成下列各题:
①已知x2﹣4y2=12,x+2y=4,求x的值.
②计算:.
11.【探究】如图1,边长为a的大正方形中有一个边长为b的小正方形,把图1中的阴影部分拼成一个长方形(如图2所示),通过观察比较图2与图1中的阴影部分面积,可以得到乘法公式 .(用含a,b的等式表示)
【应用】请应用这个公式完成下列各题:
(1)已知4m2=12+n2,2m+n=4,则2m﹣n的值为 .
(2)计算:20192﹣2020×2018.
【拓展】
计算:1002﹣992+982﹣972+…+42﹣32+22﹣12.
12.已知:a2﹣b2=(a﹣b)(a+b);a3﹣b3=(a﹣b)(a2+ab+b2);a4﹣b4=(a﹣b)(a3+a2b+ab2+b3);a5﹣b5=(a﹣b)(a4+a3b+a2b2+ab3+b4)按此规律,则:
(1)a6﹣b6=(a﹣b) ;
(2)若,请你根据上述规律求出代数式的值.
13.计算:(2x﹣y)(4x2+y2)(2x+y)
14.(2a+b)(2a﹣b)(4a2+b2)
15.计算:(a2+ab+b2)(a2﹣ab+b2).
16.当n为自然数时,(n+7)2﹣(n﹣5)2能被24整除吗?说明理由.
17.78﹣1能被40至50之间的哪一个整数整除,试说明之.
18.两个连续偶数的平方差能被4整除吗?为什么?
19.已知a﹣b=2,b﹣c=2,a+c=14,求a2﹣b2.
20.计算.
21.若(N+2035)2=123456789,求(N+2045)(N+2025)的值.
参考答案
1.解:正方形地砖的面积为a2平方厘米,长方形地砖面积为(a+3)(a﹣3)=(a2﹣9)平方厘米,
长方形面积比正方形减少了9平方厘米,
因此这种长方形地砖每块的材料成本价与正方形地砖相比减少了9b元,
故选:C.
2.解:设原正方形草坪的边长为am,则面积为a2m2,
改建后的草坪的长为(a+3),宽为(a﹣3),因此面积为(a+3)(a﹣3)=a2﹣9(m2),
因此造后的长方形草坪面积与原来正方形草坪面积差为a2﹣(a2﹣9)=9(m2),
即造后的长方形草坪面积与原来正方形草坪面积减少9m2,
故选:D.
3.解:由题意得,阴影部分的面积为:(m+3)2﹣m2=m2+6m+9﹣m2=6m+9,
∴拼成的长方形的另一边长为:(6m+9)÷3=3(2m+3)÷3=2m+3,
故选:A.
4.解:根据题意得:(a+b)(a﹣b)=a2﹣b2,
则这个矩形的面积为(a2﹣b2)m2.
故选:A.
5.解:由题可得,大正方形的周长为c1=4a,
长方形的周长为c2=2(a+b)+2(a﹣b)=4a,
∴c1与c2的大小关系是c1=c2,
故选:B.
6.解:边长a的正方体的体积=a3,
边长为b的小正方体的体积=b3,
则剩余部分的体积是:a2(a﹣b)+2b2(a﹣b)+(a﹣b)2b=(a﹣b)(a2+ab+b2)=a3﹣b3,即a3﹣b3=(a﹣b)(a2+ab+b2).
故选:B.
7.解:设原来正方形的边长是xcm.根据题意得:
(x+3)2﹣x2=33,
∴(x+3+x)(x+3﹣x)=3(2x+3)=33,
解得x=4.
∴原来这个正方形的面积是42=16(cm2).
故答案为:16.
8.解:==a+b.
故答案是:a+b.
9.解:(1)改造后长为:2a+b+2b=2a+3b,宽为:2a+b﹣2b=2a﹣b.
∴改造后的长方形草坪的面积是:(2a+3b)(2a﹣b)=4a2+4ab﹣3b2.
答:改造后的面积为:(4a2+4ab﹣3b2)平方米.
故答案为:4a2+4ab﹣3b2.
(2)改造前的面积为:(2a+b)2=4a2+4ab+b2.
∵4a2+4ab+b2﹣(4a2+4ab﹣3b2)=4b2>0.
∴改造后比改造前的面积减少了,减少了4b2平方米.
故答案为:改造后比改造前的面积减少了,减少了4b2平方米.
10.解:(1)第一个图形中阴影部分的面积是a2﹣b2,
第二个图形的面积是(a+b)(a﹣b),
则a2﹣b2=(a+b)(a﹣b).
故选:C;
(2)①∵x2﹣4y2=(x+2y)(x﹣2y),
∴12=4(x﹣2y),
得:x﹣2y=3,
联立,
①+②,得2x=7,
解得:x=;
②
=(1﹣)(1+)(1﹣)(1+)(1﹣)(1+)…(1﹣)(1+)(1﹣)(1+)
=
=×
=.
11.解:
【探究】图1中阴影部分面积a2﹣b2,图2中阴影部分面积(a+b)(a﹣b),
所以,得到乘法公式(a+b)(a﹣b)=a2﹣b2
故答案为(a+b)(a﹣b)=a2﹣b2.
【应用】
(1)由4m2=12+n2得,4m2﹣n2=12
∵(2m+n) (2m+n)=4m2﹣n2
∴2m﹣n=3
故答案为3.
(2)20192﹣2020×2018
=20192﹣(2019+1)×(2019﹣1)
=20192﹣(20192﹣1)
=20192﹣20192+1
=1
【拓展】
1002﹣992+982﹣972+…+42﹣32+22﹣12
=(100+99)×(100﹣99)+(98+97)×(98﹣97)+…+(4+3)×(4﹣3)+(2+1)×(2﹣1)
=199+195+…+7+3
=5050
12.解:(1)根据规律可知,a6﹣b6=(a﹣b)(a5+a4b+a3b2+a2b3+ab4+b5);
(2)
=(a﹣)(a2+a +)
=(a﹣)(a2+a +)
=(a﹣)(a2++1)
=(a﹣)(a2++2a ﹣2a +1)
=(a﹣)[(a2+﹣2a )+2+1]
=(a﹣)[(a﹣)2+3]
=3×(32+3)
=3×12
=36.
13.解:原式=(2x﹣y)(2x+y)(4x2+y2)
=(4x2﹣y2)(4x2+y2)
=16x4﹣y4.
14.解:原式=(4a2﹣b2)(4a2+b2)=16a4﹣b4.
15.解:(a2+ab+b2)(a2﹣ab+b2),
=(a2+b2+ab)(a2+b2﹣ab),
=(a2+b2)2﹣(ab)2,
=a4+b4+2a2b2﹣a2b2,
=a4+b4+a2b2.
16.解:因为(n+7)2﹣(n﹣5)2=(2n+2)(n+7﹣n+5)=24(n+1);
又n为自然数,故其必能被24整除.
17.解:∵78﹣1=(72﹣1)(72+1)(74+1),
=48×50×(74+1),
∴78﹣1能被40至50之间的48整除.
18.解:设两个连续偶数为2n,2n+2,则有
(2n+2)2﹣(2n)2,
=(2n+2+2n)(2n+2﹣2n),
=(4n+2)×2,
=4(2n+1),
因为n为整数,
所以4(2n+1)中的2n+1也是正整数,
所以4(2n+1)是4的倍数.
19.解:∵b﹣c=2,a+c=14,
∴a+b=16,
∵a﹣b=2,
∴a2﹣b2=(a+b)(a﹣b)=16×2=32.
20.解:原式=,
=,
=,
=,
=,
=,
=1.
21.解:∵(N+2045)(N+2025),
=[(N+2035)+10][(N+2035)﹣10],
=(N+2035)2﹣102,
(N+2035)2=123456789,
∴原式=123456789﹣100=123456689.
1.某厂原来生产一种边长为a厘米的正方形地砖,现将地砖的一边扩大3厘米,另一边缩短3厘米,改成生产长方形地砖.若材料的成本价为每平方厘米b元,则这种长方形地砖每块的材料成本价与正方形地砖相比( )
A.增加了9b元 B.增加了3ab元
C.减少了9b元 D.减少了3ab元
2.为了美化城市,经统一规划,将一正方形草坪的南北方向增加3m,东西方向缩短3m,则改造后的长方形草坪面积与原来正方形草坪面积相比( )
A.保持不变 B.增加9m2 C.增加6m2 D.减少9m2
3.如图,边长为m+3的正方形纸片剪去一个边长为m的正方形后,用剩余部分剪拼成一个长方形(不重叠无缝隙).若拼成的长方形一边长为3,则另一边长为( )
A.2m+3 B.2m+6 C.m+3 D.m+6
4.一个矩形的长为(a+b)m,宽为(a﹣b)m,则这个矩形的面积为( )
A.(a2﹣b2)m2 B.(a+b)2m2 C.(a﹣b)2m2 D.(2a﹣2b)m2
5.如图(1),在边长为a的大正方形中,剪去一个边长为b的小正方形(a>b),然后将余下的部分剪开拼成长方形,如图(2),若大正方形的周长为c1,长方形的周长为c2,则c1与c2的大小关系是( )
A.c1>c2 B.c1=c2 C.c1<c2 D.不能确定
6.如图所示,在边长为a的正方形中减去一个边长为b的小正方形(a>b),剩下的部分的面积,可得到平方差公式;那么在边长a的正方体中减去一个边长为b的小正方体(a>b),剩下的部分的体积为a3﹣b3,它等于( )
A.(a+b)(a2﹣ab+b2) B.(a﹣b)(a2+ab+b2)
C.(a﹣b)(a2+b2) D.(a+b)(a2﹣b2)
7.把一个正方形的边长增加了3cm得到的正方形的面积增加了33cm2,则原来这个正方形的面积是 cm2.
8.已知一个长方形的面积是a2﹣b2(a>b),其中短边长为a﹣b,则长边长是 .
9.学校有一块边长为(2a+b)米的正方形草坪,经统一规化后,南北方向要缩短2b米,而东西方向要加长2b米,请回答下列问题:
(1)改造后的长方形草坪的面积是多少平方米?
(2)改造后的长方形草坪的面积比改造前的面积增加了还是减少了?增加或减少了多少平方米?
10.从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)上述操作能验证的等式是 ;(请选择正确的一个)
A.a2﹣2ab+b2=(a﹣b)2 B.b2+ab=b(a+b)
C.a2﹣b2=(a+b)(a﹣b) D.a2+ab=a(a+b)
(2)应用你从(1)选出的等式,完成下列各题:
①已知x2﹣4y2=12,x+2y=4,求x的值.
②计算:.
11.【探究】如图1,边长为a的大正方形中有一个边长为b的小正方形,把图1中的阴影部分拼成一个长方形(如图2所示),通过观察比较图2与图1中的阴影部分面积,可以得到乘法公式 .(用含a,b的等式表示)
【应用】请应用这个公式完成下列各题:
(1)已知4m2=12+n2,2m+n=4,则2m﹣n的值为 .
(2)计算:20192﹣2020×2018.
【拓展】
计算:1002﹣992+982﹣972+…+42﹣32+22﹣12.
12.已知:a2﹣b2=(a﹣b)(a+b);a3﹣b3=(a﹣b)(a2+ab+b2);a4﹣b4=(a﹣b)(a3+a2b+ab2+b3);a5﹣b5=(a﹣b)(a4+a3b+a2b2+ab3+b4)按此规律,则:
(1)a6﹣b6=(a﹣b) ;
(2)若,请你根据上述规律求出代数式的值.
13.计算:(2x﹣y)(4x2+y2)(2x+y)
14.(2a+b)(2a﹣b)(4a2+b2)
15.计算:(a2+ab+b2)(a2﹣ab+b2).
16.当n为自然数时,(n+7)2﹣(n﹣5)2能被24整除吗?说明理由.
17.78﹣1能被40至50之间的哪一个整数整除,试说明之.
18.两个连续偶数的平方差能被4整除吗?为什么?
19.已知a﹣b=2,b﹣c=2,a+c=14,求a2﹣b2.
20.计算.
21.若(N+2035)2=123456789,求(N+2045)(N+2025)的值.
参考答案
1.解:正方形地砖的面积为a2平方厘米,长方形地砖面积为(a+3)(a﹣3)=(a2﹣9)平方厘米,
长方形面积比正方形减少了9平方厘米,
因此这种长方形地砖每块的材料成本价与正方形地砖相比减少了9b元,
故选:C.
2.解:设原正方形草坪的边长为am,则面积为a2m2,
改建后的草坪的长为(a+3),宽为(a﹣3),因此面积为(a+3)(a﹣3)=a2﹣9(m2),
因此造后的长方形草坪面积与原来正方形草坪面积差为a2﹣(a2﹣9)=9(m2),
即造后的长方形草坪面积与原来正方形草坪面积减少9m2,
故选:D.
3.解:由题意得,阴影部分的面积为:(m+3)2﹣m2=m2+6m+9﹣m2=6m+9,
∴拼成的长方形的另一边长为:(6m+9)÷3=3(2m+3)÷3=2m+3,
故选:A.
4.解:根据题意得:(a+b)(a﹣b)=a2﹣b2,
则这个矩形的面积为(a2﹣b2)m2.
故选:A.
5.解:由题可得,大正方形的周长为c1=4a,
长方形的周长为c2=2(a+b)+2(a﹣b)=4a,
∴c1与c2的大小关系是c1=c2,
故选:B.
6.解:边长a的正方体的体积=a3,
边长为b的小正方体的体积=b3,
则剩余部分的体积是:a2(a﹣b)+2b2(a﹣b)+(a﹣b)2b=(a﹣b)(a2+ab+b2)=a3﹣b3,即a3﹣b3=(a﹣b)(a2+ab+b2).
故选:B.
7.解:设原来正方形的边长是xcm.根据题意得:
(x+3)2﹣x2=33,
∴(x+3+x)(x+3﹣x)=3(2x+3)=33,
解得x=4.
∴原来这个正方形的面积是42=16(cm2).
故答案为:16.
8.解:==a+b.
故答案是:a+b.
9.解:(1)改造后长为:2a+b+2b=2a+3b,宽为:2a+b﹣2b=2a﹣b.
∴改造后的长方形草坪的面积是:(2a+3b)(2a﹣b)=4a2+4ab﹣3b2.
答:改造后的面积为:(4a2+4ab﹣3b2)平方米.
故答案为:4a2+4ab﹣3b2.
(2)改造前的面积为:(2a+b)2=4a2+4ab+b2.
∵4a2+4ab+b2﹣(4a2+4ab﹣3b2)=4b2>0.
∴改造后比改造前的面积减少了,减少了4b2平方米.
故答案为:改造后比改造前的面积减少了,减少了4b2平方米.
10.解:(1)第一个图形中阴影部分的面积是a2﹣b2,
第二个图形的面积是(a+b)(a﹣b),
则a2﹣b2=(a+b)(a﹣b).
故选:C;
(2)①∵x2﹣4y2=(x+2y)(x﹣2y),
∴12=4(x﹣2y),
得:x﹣2y=3,
联立,
①+②,得2x=7,
解得:x=;
②
=(1﹣)(1+)(1﹣)(1+)(1﹣)(1+)…(1﹣)(1+)(1﹣)(1+)
=
=×
=.
11.解:
【探究】图1中阴影部分面积a2﹣b2,图2中阴影部分面积(a+b)(a﹣b),
所以,得到乘法公式(a+b)(a﹣b)=a2﹣b2
故答案为(a+b)(a﹣b)=a2﹣b2.
【应用】
(1)由4m2=12+n2得,4m2﹣n2=12
∵(2m+n) (2m+n)=4m2﹣n2
∴2m﹣n=3
故答案为3.
(2)20192﹣2020×2018
=20192﹣(2019+1)×(2019﹣1)
=20192﹣(20192﹣1)
=20192﹣20192+1
=1
【拓展】
1002﹣992+982﹣972+…+42﹣32+22﹣12
=(100+99)×(100﹣99)+(98+97)×(98﹣97)+…+(4+3)×(4﹣3)+(2+1)×(2﹣1)
=199+195+…+7+3
=5050
12.解:(1)根据规律可知,a6﹣b6=(a﹣b)(a5+a4b+a3b2+a2b3+ab4+b5);
(2)
=(a﹣)(a2+a +)
=(a﹣)(a2+a +)
=(a﹣)(a2++1)
=(a﹣)(a2++2a ﹣2a +1)
=(a﹣)[(a2+﹣2a )+2+1]
=(a﹣)[(a﹣)2+3]
=3×(32+3)
=3×12
=36.
13.解:原式=(2x﹣y)(2x+y)(4x2+y2)
=(4x2﹣y2)(4x2+y2)
=16x4﹣y4.
14.解:原式=(4a2﹣b2)(4a2+b2)=16a4﹣b4.
15.解:(a2+ab+b2)(a2﹣ab+b2),
=(a2+b2+ab)(a2+b2﹣ab),
=(a2+b2)2﹣(ab)2,
=a4+b4+2a2b2﹣a2b2,
=a4+b4+a2b2.
16.解:因为(n+7)2﹣(n﹣5)2=(2n+2)(n+7﹣n+5)=24(n+1);
又n为自然数,故其必能被24整除.
17.解:∵78﹣1=(72﹣1)(72+1)(74+1),
=48×50×(74+1),
∴78﹣1能被40至50之间的48整除.
18.解:设两个连续偶数为2n,2n+2,则有
(2n+2)2﹣(2n)2,
=(2n+2+2n)(2n+2﹣2n),
=(4n+2)×2,
=4(2n+1),
因为n为整数,
所以4(2n+1)中的2n+1也是正整数,
所以4(2n+1)是4的倍数.
19.解:∵b﹣c=2,a+c=14,
∴a+b=16,
∵a﹣b=2,
∴a2﹣b2=(a+b)(a﹣b)=16×2=32.
20.解:原式=,
=,
=,
=,
=,
=,
=1.
21.解:∵(N+2045)(N+2025),
=[(N+2035)+10][(N+2035)﹣10],
=(N+2035)2﹣102,
(N+2035)2=123456789,
∴原式=123456789﹣100=123456689.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
