24.1.3《圆心角定理》
文档属性
| 名称 | 24.1.3《圆心角定理》 |

|
|
| 格式 | zip | ||
| 文件大小 | 114.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-14 00:00:00 | ||
图片预览





文档简介
课件31张PPT。人教版教材九年级数学
圆心角定理山东省邹平实验中学复习回忆1:垂径定理的内容是什么?
2:垂径定理的推论内容是什么?
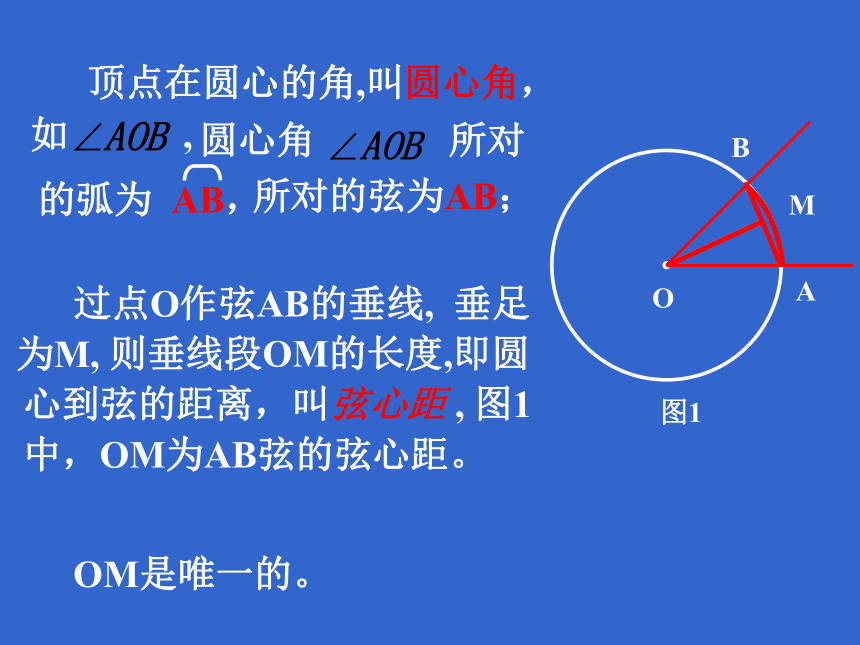
3:圆的对称性 过点O作弦AB的垂线, 垂足
为M,AB所对的弦为AB;图1 OM是唯一的。 则垂线段OM的长度,即圆
心到弦的距离,叫弦心距 , 图1
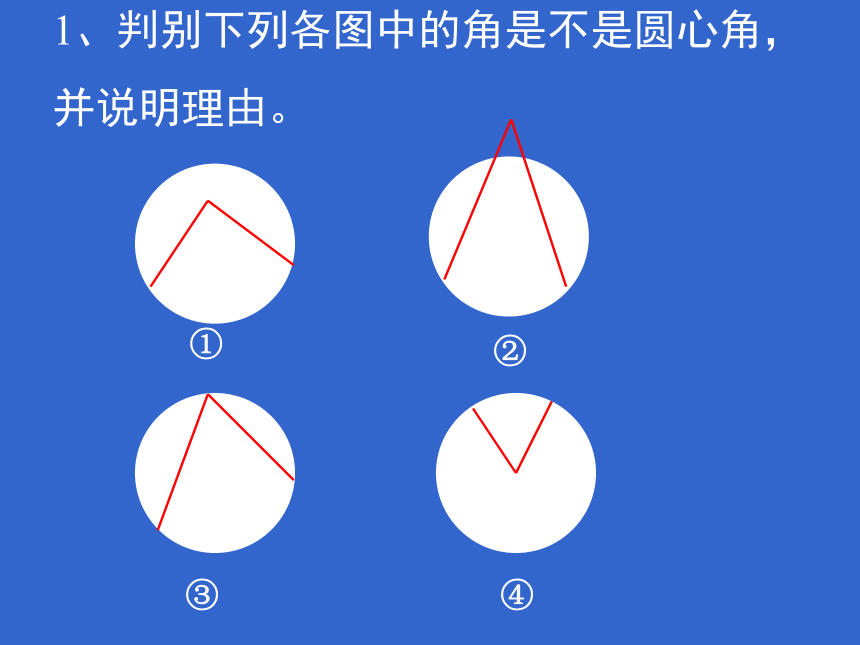
中,OM为AB弦的弦心距。1、判别下列各图中的角是不是圆心角,
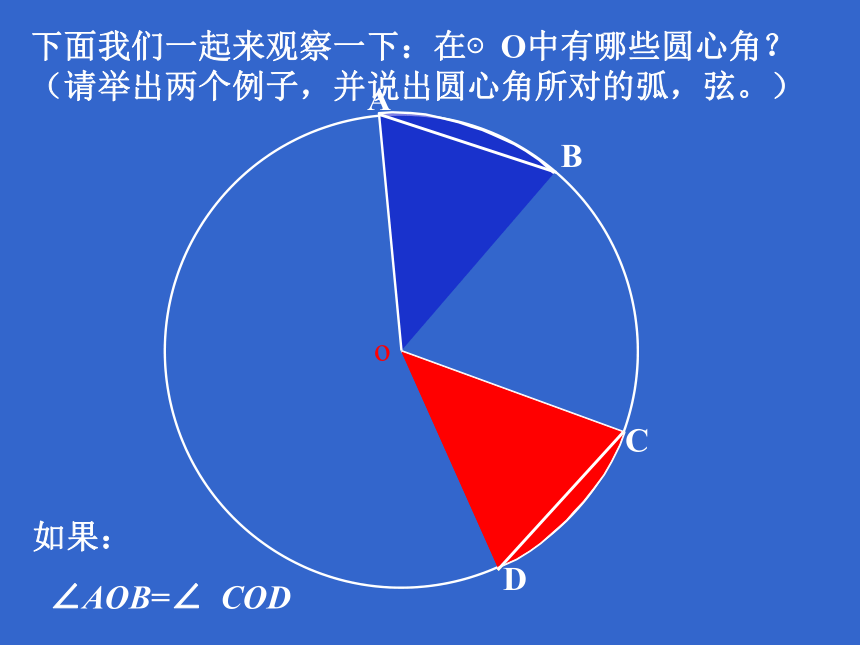
并说明理由。①②③④2、下列图中弦心距做对了的是( )┐┐①②③④ABCDo下面我们一起来观察一下:在⊙O中有哪些圆心角?(请举出两个例子,并说出圆心角所对的弧,弦。)如果:
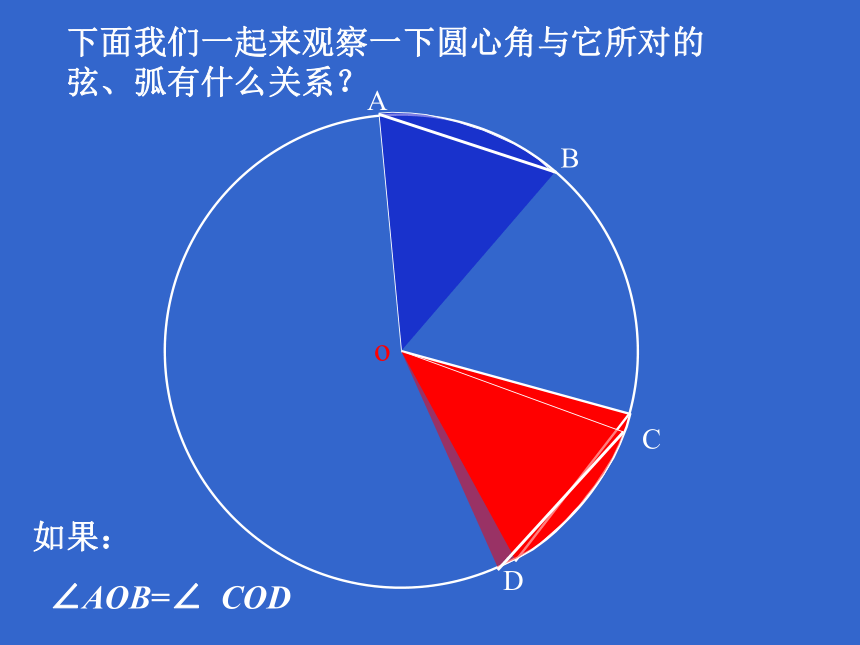
∠AOB=∠ CODABCDo下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系?如果:
∠AOB=∠ CODABCDo下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系?如果:
∠AOB=∠ CODABCDo下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系?如果:
∠AOB=∠ CODABCDo下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系?如果:
∠AOB=∠ CODABCDo下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系?如果:
∠AOB=∠ CODABCDo下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系?如果:
∠AOB=∠ CODABCDo下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系?如果:
∠AOB=∠ CODABCDo下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系?如果:
∠AOB=∠ CODABCDo下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系?如果:
∠AOB=∠ CODABCDo下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系?如果:
∠AOB=∠ CODABCDo下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系?如果:
∠AOB=∠ CODABCDo下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系?如果:
∠AOB=∠ CODABCDo下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系?如果:
∠AOB=∠ COD
证明:∵OA=OC ,OB=OD,
∠AOB=∠COD,
∴ 当点A与点C重合时,
点B与点D也重合。
∴ AB=CD,
圆心角定理:在同圆或等圆中,
相等的圆心角所对的弧相等,所对的弦也相等。 已知:如图∠AOB=∠ COD,
求证: AB=CD,AB = CD。⌒⌒如图,⊙O 和⊙O' 是等圆,
如果 ∠AOB= ∠ A'O'B'
那么 AB=A'B' 、AB= A'B' 、OM=O'M',
为什么????圆心角定理 :
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等。对于等圆的情况 ,因为两个等圆可叠合成同圆,所以等圆问题可转化为同圆问题,命题成立。条件结论在同圆或等圆中
如果圆心角相等那么圆心角所对的弧相等圆心角所对的弦相等圆心角所对的弦的弦心距相等圆心角, 弧,弦,弦心距之间的关系定理在同圆或等圆中,相等的圆心角所对的弧相等所对的弦相等,所对的弦的弦心距相等.由条件:
①∠AOB=∠A′O′B′③AB=A′B′④ OD=O′D′请大家思考一下这个定理的逆命题推论:(圆心角定理的逆定理)
在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们所对应的其余的各组量都分别相等。1、已知:如图,AB、CD是⊙O的两条弦,OE、OF为AB、CD的弦心距,根据本节定理及推论填空:
(1)如果AB=CD,那么
_____________,________,____________。
(2)如果OE=OF,那么
_____________,________,____________。
(3)如果AB=CD 那么
______________,__________,____________。
(4)如果∠AOB=∠COD,那么
_________,________,_________。⌒
⌒
∠AOB=∠COD OE=OF AB=CD
⌒⌒∠AOB=∠COD AB=CD AB=CD⌒
⌒
∠AOB=∠COD AB=CD OE=OF巩固练习:做一做2.已知:如图,在⊙O中,弦AB=CD.
求证:AD=BC 3.已知AB是⊙O的直径,M.N是AO.BO的中点。CM⊥AB,DN⊥AB,分别与圆交于C.D点。
求证:⌒ ⌒AC=BD随堂训练本课结束,谢谢大家
圆心角定理山东省邹平实验中学复习回忆1:垂径定理的内容是什么?
2:垂径定理的推论内容是什么?
3:圆的对称性 过点O作弦AB的垂线, 垂足
为M,AB所对的弦为AB;图1 OM是唯一的。 则垂线段OM的长度,即圆
心到弦的距离,叫弦心距 , 图1
中,OM为AB弦的弦心距。1、判别下列各图中的角是不是圆心角,
并说明理由。①②③④2、下列图中弦心距做对了的是( )┐┐①②③④ABCDo下面我们一起来观察一下:在⊙O中有哪些圆心角?(请举出两个例子,并说出圆心角所对的弧,弦。)如果:
∠AOB=∠ CODABCDo下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系?如果:
∠AOB=∠ CODABCDo下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系?如果:
∠AOB=∠ CODABCDo下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系?如果:
∠AOB=∠ CODABCDo下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系?如果:
∠AOB=∠ CODABCDo下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系?如果:
∠AOB=∠ CODABCDo下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系?如果:
∠AOB=∠ CODABCDo下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系?如果:
∠AOB=∠ CODABCDo下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系?如果:
∠AOB=∠ CODABCDo下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系?如果:
∠AOB=∠ CODABCDo下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系?如果:
∠AOB=∠ CODABCDo下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系?如果:
∠AOB=∠ CODABCDo下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系?如果:
∠AOB=∠ CODABCDo下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系?如果:
∠AOB=∠ COD
证明:∵OA=OC ,OB=OD,
∠AOB=∠COD,
∴ 当点A与点C重合时,
点B与点D也重合。
∴ AB=CD,
圆心角定理:在同圆或等圆中,
相等的圆心角所对的弧相等,所对的弦也相等。 已知:如图∠AOB=∠ COD,
求证: AB=CD,AB = CD。⌒⌒如图,⊙O 和⊙O' 是等圆,
如果 ∠AOB= ∠ A'O'B'
那么 AB=A'B' 、AB= A'B' 、OM=O'M',
为什么????圆心角定理 :
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等。对于等圆的情况 ,因为两个等圆可叠合成同圆,所以等圆问题可转化为同圆问题,命题成立。条件结论在同圆或等圆中
如果圆心角相等那么圆心角所对的弧相等圆心角所对的弦相等圆心角所对的弦的弦心距相等圆心角, 弧,弦,弦心距之间的关系定理在同圆或等圆中,相等的圆心角所对的弧相等所对的弦相等,所对的弦的弦心距相等.由条件:
①∠AOB=∠A′O′B′③AB=A′B′④ OD=O′D′请大家思考一下这个定理的逆命题推论:(圆心角定理的逆定理)
在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们所对应的其余的各组量都分别相等。1、已知:如图,AB、CD是⊙O的两条弦,OE、OF为AB、CD的弦心距,根据本节定理及推论填空:
(1)如果AB=CD,那么
_____________,________,____________。
(2)如果OE=OF,那么
_____________,________,____________。
(3)如果AB=CD 那么
______________,__________,____________。
(4)如果∠AOB=∠COD,那么
_________,________,_________。⌒
⌒
∠AOB=∠COD OE=OF AB=CD
⌒⌒∠AOB=∠COD AB=CD AB=CD⌒
⌒
∠AOB=∠COD AB=CD OE=OF巩固练习:做一做2.已知:如图,在⊙O中,弦AB=CD.
求证:AD=BC 3.已知AB是⊙O的直径,M.N是AO.BO的中点。CM⊥AB,DN⊥AB,分别与圆交于C.D点。
求证:⌒ ⌒AC=BD随堂训练本课结束,谢谢大家
同课章节目录
