2021-2022学年青岛版七年级上学期数学期末练习试卷 (word版含解析)
文档属性
| 名称 | 2021-2022学年青岛版七年级上学期数学期末练习试卷 (word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 123.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-17 00:00:00 | ||
图片预览




文档简介
2021-2022学年青岛新版七年级上学期数学期末练习试卷
一.选择题(共12小题,满分36分,每小题3分)
1.下列各式不成立的是( )
A.|﹣2|=2 B.|+2|=|﹣2| C.﹣|﹣3|=﹣3 D.﹣|2|=|﹣2|
2.在“十一五”期间,中国减少二氧化碳排放1 460 000 000吨,赢得国际社会广泛赞誉.将1 460 000 000用科学记数法表示为( )
A.146×107 B.1.46×107 C.1.46×109 D.1.46×1010
3.在方程:①3x﹣y=2;②x+=1;③=1;④x=0;⑤x2﹣2x﹣3=0;⑥=中,是一元一次方程的有( )个.
A.4 B.3 C.2 D.1
4.单项式的系数和次数分别是( )
A.﹣2,3 B.﹣2,2 C.﹣,3 D.﹣,2
5.要想了解九年级1000名考生的数学成绩,从中抽取了100名考生的数学成绩进行统计分析,以下说法正确的是( )
A.这100名考生是总体的一个样本
B.每位考生的数学成绩是个体
C.1000名考生是总体
D.100名考生是样本的容量
6.当x=3,y=2时,代数式的值是( )
A. B.2 C.0 D.3
7.如图是正方体的表面展开图,在正方形的A处填一个数,使它和相对面的数为相反数( )
A.2 B.3 C.﹣3 D.﹣2
8.如图,延长线段AB到点C,使BC=2AB,D是AC的中点,若AB=6,则BD的长为( )
A.2 B.2.5 C.3 D.3.5
9.我校七年级学生总人数为700,其男女生所占比例如图所示,则该校七年级男生人数为( )
A.48 B.52 C.336 D.364
10.实数a、b、c在数轴上的位置如图所示,则代数式|a|﹣|a+b|+|c﹣a|+|b﹣c|的值等于( )
A.a B.2a﹣2b C.2c﹣a D.﹣a
11.某商场购进一批服装,每件服装销售的标价为400元,由于换季滞销,商场决定将这种服装按标价的六折销售,若打折后每件服装仍能获利20%,则该服装的进价是( )
A.160元 B.180元 C.200元 D.220元
12.如图,圆上有五个点,这五个点将圆分成五等份(每一份称为一段弧长),把这五个点按顺时针方向依次编号为1,2,3,4,5,若从某一点开始,沿圆周顺时针方向行走,点的编号是数字几,就走几段弧长,我们把这种走法称为一次“移位”.如:小明在编号为3的点,那么他应走3段弧长,即从3→4→5→1为第1次“移位”,这时他到达编号为1的点,那么他应走1段弧长,即从1→2为第2次“移位”.若小明从编号为4的点开始,经过2019次“移位”后,他到达编号为( )
A.1 B.2 C.4 D.5
二.填空题(共6小题,满分18分,每小题3分)
13.如图所示的立体图形的名称是 .
14.若单项式与3x5yn+2的和仍是单项式,则mn= .
15.若|a|=5,b=﹣3,且a+b>0,则ab= .
16.如图所示是计算机程序计算,若开始输入x=﹣1,则最后输出的结果是 ;
17.请阅读下面材料,现规定一种运算:||=ad﹣bc,例如=2×5﹣3×4=10﹣12=﹣2,按照这种运算的规定,当x= 时,=.
18.某体育器材商场以a元/台的价格购进一种家用健身器材,提价60%作为标价后,为了迎合消费者的心理,再按八折促销,在不考虑其他因素的前提下,每售出一台该器材商场可获利 元.
三.解答题(共7小题,满分66分)
19.(14分)(1)先化简,再求值(3a2b﹣ab2)+(ab2+5a2b),其中a=2,b=﹣1.
(2)若a,b互为相反数,c,d互为倒数,m的绝对值是3,求的值.
20.(10分)解方程:
(1)2(x﹣1)=2﹣5(x+2);
(2).
21.(7分)如图,点C,D在线段AB上,且满足CD=AD=BC,点E、F分别为线段AC,BD的中点,如果EF=5cm,求线段AB的长度.
22.(7分)某汽车经销公司计划经销A、B两种品牌的轿车50辆,该公司经销这50辆轿车的成本不少于1240万元,但不超过1244万元,两种轿车的成本和售价如下表.
A B
成本(万元/辆) 24 26
售价(万元/辆) 27 30
(1)该公司经销这两种品牌轿车有哪几种方案,哪种方案获利最大,最大利润是多少?
(2)根据市场调查,一段时期内,B牌轿车售价不会改变,每辆A牌轿车的售价将会提高a万元(0<a<1.2),且所有两种轿车全部售出,哪种经销方案获利最大?(注:利润=售价﹣成本)
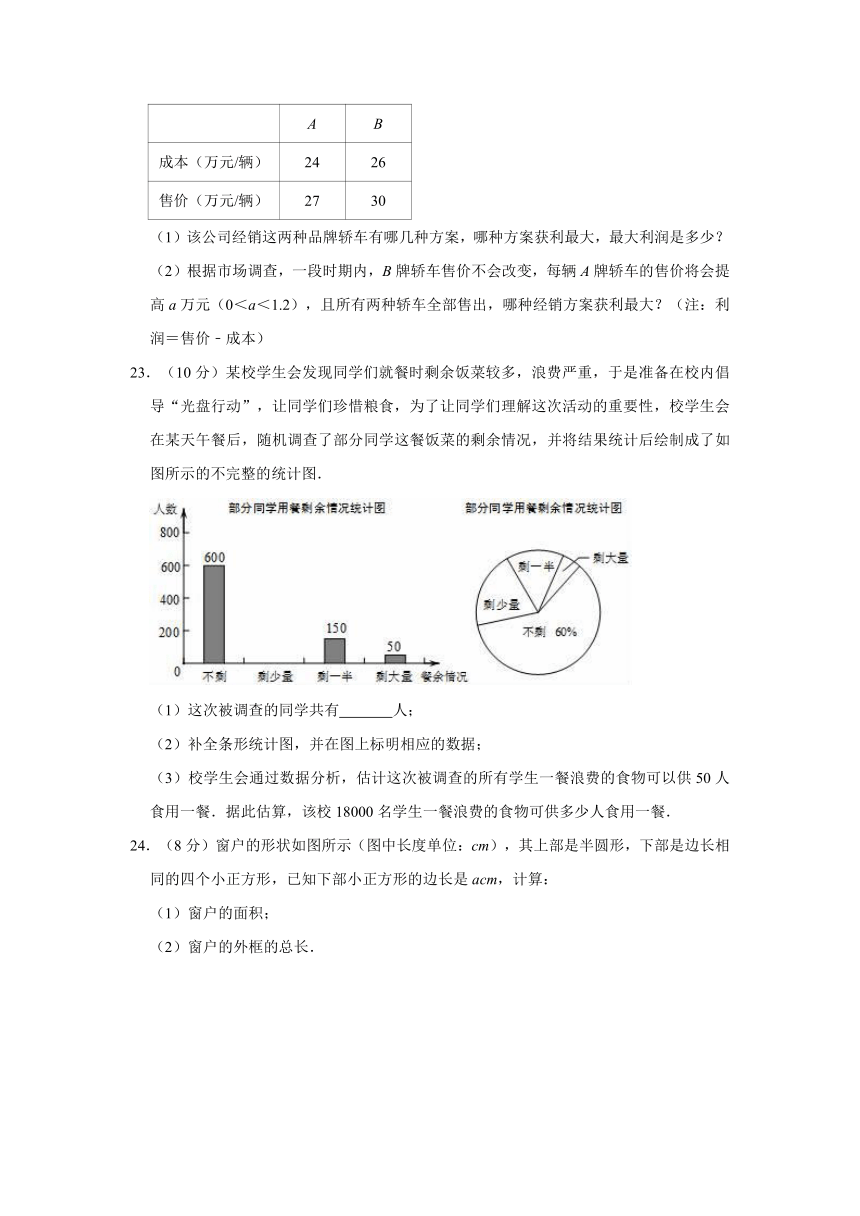
23.(10分)某校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食,为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图.
(1)这次被调查的同学共有 人;
(2)补全条形统计图,并在图上标明相应的数据;
(3)校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供50人食用一餐.据此估算,该校18000名学生一餐浪费的食物可供多少人食用一餐.
24.(8分)窗户的形状如图所示(图中长度单位:cm),其上部是半圆形,下部是边长相同的四个小正方形,已知下部小正方形的边长是acm,计算:
(1)窗户的面积;
(2)窗户的外框的总长.
25.(10分)小明骑自行车的速度是15千米/小时,一天,小明从家出发骑自行车去学校,恰好准时达到,如果他全程乘坐速度为40千米/小时的公共汽车,则会提前15分钟达到学校.
(1)小明家离学校有多少千米;
(2)小明乘坐公共汽车上学需要多长时间?
参考答案与试题解析
一.选择题(共12小题,满分36分,每小题3分)
1.解:A.∵=2正确,
故A选项成立,不符合题目要求;
B.∵=正确,
故B选项成立,不符合题目要求;
C.∵﹣=﹣3正确,
故C选项成立,不符合题目要求;
D.∵﹣=错误,
∴D选项不成立,符合题目要求;
故选:D.
2.解:将1 460 000 000用科学记数法表示为:1.46×109.
故选:C.
3.解:③=1、④x=0、⑥=符合一元一次方程的定义,故符合题意.
①3x﹣y=2是二元一次方程,故不符合题意;
②x+=1是分式方程,故不符合题意;
⑤x2﹣2x﹣3=0是关于x的一元二次方程,故不符合题意.
故选:B.
4.解:根据单项式系数和次数的定义,单项式的系数为﹣,次数是3;
故选:C.
5.解:A、这100名考生的数学成绩是总体的一个样本,故本选项不合题意;
B、每位考生的数学成绩是个体,故本选项符合题意;
C、1000名考生的数学成绩是总体,故本选项不合题意;
D、样本的容量是100,故本选项不合题意.
故选:B.
6.解:==
7.解:“2”与“5”相对,“A”与“3”相对,“1”与“4”相对,
故A=﹣3.
故选:C.
8.解:∵AB=6,BC=2AB=12,
∴AC=AB+BC=6+12=18,
∵D是AC的中点,
∴AD=AC==9,
∴BD=AD﹣AB=9﹣6=3.
故选:C.
9.解:该校七年级男生人数=700×52%=364(人).
故选:D.
10.解:由数轴上点的位置得:b<a<0<c,
∴a+b<0,c﹣a>0,b﹣c<0,
则|a|﹣|a+b|+|c﹣a|+|b﹣c|=﹣a+a+b+c﹣a+c﹣b=2c﹣a.
故选:C.
11.解:设这件服装每件的进价为a元,依题意有,
(1+20%)a=400×0.6,
解得a=200.
答:该服装每件的进价为200元.
故选:C.
12.解:从编号为4的点开始走4段弧:4→5→1→2→3,所以第一次“移位”他到达编号为3的点;
第二次移位后:3→4→5→1,到编号为1的点;
第三次移位后:1→2,到编号为2的点;
第四次移位后:2→3→4,回到起点;
可以发现:他的位置以“3,1,2,4,”循环出现,
2019÷4=504…3,
所以第2019次移位后他的编号与第三次相同,到达编号为2的点;
故选:B.
二.填空题(共6小题,满分18分,每小题3分)
13.解:∵该立体图形上面和底面都是三角形,且有三条棱,
∴它的名称是三棱柱,
故答案为:三棱柱.
14.解:∵﹣ x2m﹣3y4与3x5yn+2的和仍是单项式,
∴﹣x2m﹣3y4与3x5yn+2是同类项.
∴2m﹣3=5,n+2=4.
解得:m=4,n=2.
∴mn=8.
故答案为:8.
15.解:∵|a|=5,
∴a=±5,
∵b=﹣3,a+b>0,
∴a=5,
∴ab=5×(﹣3)=﹣15,
故答案为﹣15.
16.解:如图所示,
∵当x=﹣1时,1+x﹣2x2=1﹣1﹣2=﹣2>﹣5,
∴输入x=﹣2,
∴1+x﹣2x2=1﹣2﹣8=﹣9<﹣5,
∴输出的结果为﹣9.
故答案为﹣9.
17.解:根据题意得:2x﹣+x=,
去分母得:4x﹣1+2x=3,
解得:x=.
故答案为:
18.解:∵进价为a元/台的体育健身器材,提价60%后的标价为:(1 十60%)a=1.6a元,
∴打八折优惠后的售价为:
0.8(1+60%)a=0.8 x 1.6a=1.28a元,
∴每售出一台可获的利润为:1.28a﹣a=0.28a元,
故答案为:0.28a.
三.解答题(共7小题,满分66分)
19.解:(1)原式=3a2b﹣ab2+ab2+5a2b=8a2b,
当a=2,b=﹣1时,原式=8×22×(﹣1)=﹣32;
(2)∵a,b互为相反数,c,d互为倒数,m的绝对值是3,
∴a+b=0,cd=1,m=3或﹣3,
当m=3时,原式=0+3﹣1=2;
当m=﹣3时,原式=0﹣3﹣1=﹣4,
则原式的值为2或﹣4.
20.解:(1)去括号得:2x﹣2=2﹣5x﹣10,
移项得:2x+5x=2﹣10+2,
合并得:7x=﹣6,
解得:x=﹣;
(2)去分母得:2(5x+1)﹣(7x+2)=4,
去括号得:10x+2﹣7x﹣2=4,
移项得:10x﹣7x=4﹣2+2,
合并得:3x=4,
解得:x=.
21.解:∵CD=AD=BC,
∴AD=4CD,BC=6CD,
则AC=3CD,BD=5CD,AB=9CD;
∵点E、F分别为线段AC,BD的中点,
∴EC=AC=CD,DF=BD=CD;
∵EF=5cm,
∴EF=EC+CD+DF=CD+CD+CD=5CD,
∴CD=1cm,
∴AB=9CD=9×1=9(cm).
22.解:(1)设经销A品牌轿车x辆,则经销B品牌轿车(50﹣x)辆,根据题意得
解这个不等式组得28≤x≤30
∴该公司经销这两种品牌轿车的方案有三种,即
方案一:经销A种品牌轿车28辆,B种品牌轿车22辆,
方案二:经销A种品牌轿车29辆,B种品牌轿车21辆,
方案三:经销A种品牌轿车30辆,B种品牌轿车20辆.
方案一获利(27﹣24)×28+(30﹣26)×22=172万元,
方案二获利(27﹣24)×29+(30﹣26)×21=171万元,
方案三获利(27﹣24)×30+(30﹣26)×20=170万元.
∴方案一获利最大,最大利润是172万元;
(2)方案一获利(a+3)×28+4×22=172+28a万元,
方案二获利(a+3)×29+4×21=171+29a万元,
方案三获利(a+3)×30+4×20=170+30a万元.
当0<a<1时,方案一获利最大,
当a=1时,三种方案获利一样大,
当1<a<1.2时,方案三获利最大.
23.解:(1)这次被调查的学生共有600÷60%=1000人,
故答案为:1000;
(2)剩少量的人数为1000﹣(600+150+50)=200人,
补全条形图如下:
(3),
答:估计该校18000名学生一餐浪费的食物可供900人食用一餐.
24.解:(1)窗户的面积是:
4a2+πa2÷2
=4a2+0.5πa2
=(4+0.5π)a2(cm2)
(2)窗户的外框的总长是:
2a×3+πa
=6a+πa
=(6+π)a(cm)
25.解:(1)设小明家离学校有x千米,根据题意得:
=+,
解得x=6,
答:小明家离学校有6千米;
(2)小明乘坐公共汽车上学需要6÷40=(小时).
一.选择题(共12小题,满分36分,每小题3分)
1.下列各式不成立的是( )
A.|﹣2|=2 B.|+2|=|﹣2| C.﹣|﹣3|=﹣3 D.﹣|2|=|﹣2|
2.在“十一五”期间,中国减少二氧化碳排放1 460 000 000吨,赢得国际社会广泛赞誉.将1 460 000 000用科学记数法表示为( )
A.146×107 B.1.46×107 C.1.46×109 D.1.46×1010
3.在方程:①3x﹣y=2;②x+=1;③=1;④x=0;⑤x2﹣2x﹣3=0;⑥=中,是一元一次方程的有( )个.
A.4 B.3 C.2 D.1
4.单项式的系数和次数分别是( )
A.﹣2,3 B.﹣2,2 C.﹣,3 D.﹣,2
5.要想了解九年级1000名考生的数学成绩,从中抽取了100名考生的数学成绩进行统计分析,以下说法正确的是( )
A.这100名考生是总体的一个样本
B.每位考生的数学成绩是个体
C.1000名考生是总体
D.100名考生是样本的容量
6.当x=3,y=2时,代数式的值是( )
A. B.2 C.0 D.3
7.如图是正方体的表面展开图,在正方形的A处填一个数,使它和相对面的数为相反数( )
A.2 B.3 C.﹣3 D.﹣2
8.如图,延长线段AB到点C,使BC=2AB,D是AC的中点,若AB=6,则BD的长为( )
A.2 B.2.5 C.3 D.3.5
9.我校七年级学生总人数为700,其男女生所占比例如图所示,则该校七年级男生人数为( )
A.48 B.52 C.336 D.364
10.实数a、b、c在数轴上的位置如图所示,则代数式|a|﹣|a+b|+|c﹣a|+|b﹣c|的值等于( )
A.a B.2a﹣2b C.2c﹣a D.﹣a
11.某商场购进一批服装,每件服装销售的标价为400元,由于换季滞销,商场决定将这种服装按标价的六折销售,若打折后每件服装仍能获利20%,则该服装的进价是( )
A.160元 B.180元 C.200元 D.220元
12.如图,圆上有五个点,这五个点将圆分成五等份(每一份称为一段弧长),把这五个点按顺时针方向依次编号为1,2,3,4,5,若从某一点开始,沿圆周顺时针方向行走,点的编号是数字几,就走几段弧长,我们把这种走法称为一次“移位”.如:小明在编号为3的点,那么他应走3段弧长,即从3→4→5→1为第1次“移位”,这时他到达编号为1的点,那么他应走1段弧长,即从1→2为第2次“移位”.若小明从编号为4的点开始,经过2019次“移位”后,他到达编号为( )
A.1 B.2 C.4 D.5
二.填空题(共6小题,满分18分,每小题3分)
13.如图所示的立体图形的名称是 .
14.若单项式与3x5yn+2的和仍是单项式,则mn= .
15.若|a|=5,b=﹣3,且a+b>0,则ab= .
16.如图所示是计算机程序计算,若开始输入x=﹣1,则最后输出的结果是 ;
17.请阅读下面材料,现规定一种运算:||=ad﹣bc,例如=2×5﹣3×4=10﹣12=﹣2,按照这种运算的规定,当x= 时,=.
18.某体育器材商场以a元/台的价格购进一种家用健身器材,提价60%作为标价后,为了迎合消费者的心理,再按八折促销,在不考虑其他因素的前提下,每售出一台该器材商场可获利 元.
三.解答题(共7小题,满分66分)
19.(14分)(1)先化简,再求值(3a2b﹣ab2)+(ab2+5a2b),其中a=2,b=﹣1.
(2)若a,b互为相反数,c,d互为倒数,m的绝对值是3,求的值.
20.(10分)解方程:
(1)2(x﹣1)=2﹣5(x+2);
(2).
21.(7分)如图,点C,D在线段AB上,且满足CD=AD=BC,点E、F分别为线段AC,BD的中点,如果EF=5cm,求线段AB的长度.
22.(7分)某汽车经销公司计划经销A、B两种品牌的轿车50辆,该公司经销这50辆轿车的成本不少于1240万元,但不超过1244万元,两种轿车的成本和售价如下表.
A B
成本(万元/辆) 24 26
售价(万元/辆) 27 30
(1)该公司经销这两种品牌轿车有哪几种方案,哪种方案获利最大,最大利润是多少?
(2)根据市场调查,一段时期内,B牌轿车售价不会改变,每辆A牌轿车的售价将会提高a万元(0<a<1.2),且所有两种轿车全部售出,哪种经销方案获利最大?(注:利润=售价﹣成本)
23.(10分)某校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食,为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图.
(1)这次被调查的同学共有 人;
(2)补全条形统计图,并在图上标明相应的数据;
(3)校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供50人食用一餐.据此估算,该校18000名学生一餐浪费的食物可供多少人食用一餐.
24.(8分)窗户的形状如图所示(图中长度单位:cm),其上部是半圆形,下部是边长相同的四个小正方形,已知下部小正方形的边长是acm,计算:
(1)窗户的面积;
(2)窗户的外框的总长.
25.(10分)小明骑自行车的速度是15千米/小时,一天,小明从家出发骑自行车去学校,恰好准时达到,如果他全程乘坐速度为40千米/小时的公共汽车,则会提前15分钟达到学校.
(1)小明家离学校有多少千米;
(2)小明乘坐公共汽车上学需要多长时间?
参考答案与试题解析
一.选择题(共12小题,满分36分,每小题3分)
1.解:A.∵=2正确,
故A选项成立,不符合题目要求;
B.∵=正确,
故B选项成立,不符合题目要求;
C.∵﹣=﹣3正确,
故C选项成立,不符合题目要求;
D.∵﹣=错误,
∴D选项不成立,符合题目要求;
故选:D.
2.解:将1 460 000 000用科学记数法表示为:1.46×109.
故选:C.
3.解:③=1、④x=0、⑥=符合一元一次方程的定义,故符合题意.
①3x﹣y=2是二元一次方程,故不符合题意;
②x+=1是分式方程,故不符合题意;
⑤x2﹣2x﹣3=0是关于x的一元二次方程,故不符合题意.
故选:B.
4.解:根据单项式系数和次数的定义,单项式的系数为﹣,次数是3;
故选:C.
5.解:A、这100名考生的数学成绩是总体的一个样本,故本选项不合题意;
B、每位考生的数学成绩是个体,故本选项符合题意;
C、1000名考生的数学成绩是总体,故本选项不合题意;
D、样本的容量是100,故本选项不合题意.
故选:B.
6.解:==
7.解:“2”与“5”相对,“A”与“3”相对,“1”与“4”相对,
故A=﹣3.
故选:C.
8.解:∵AB=6,BC=2AB=12,
∴AC=AB+BC=6+12=18,
∵D是AC的中点,
∴AD=AC==9,
∴BD=AD﹣AB=9﹣6=3.
故选:C.
9.解:该校七年级男生人数=700×52%=364(人).
故选:D.
10.解:由数轴上点的位置得:b<a<0<c,
∴a+b<0,c﹣a>0,b﹣c<0,
则|a|﹣|a+b|+|c﹣a|+|b﹣c|=﹣a+a+b+c﹣a+c﹣b=2c﹣a.
故选:C.
11.解:设这件服装每件的进价为a元,依题意有,
(1+20%)a=400×0.6,
解得a=200.
答:该服装每件的进价为200元.
故选:C.
12.解:从编号为4的点开始走4段弧:4→5→1→2→3,所以第一次“移位”他到达编号为3的点;
第二次移位后:3→4→5→1,到编号为1的点;
第三次移位后:1→2,到编号为2的点;
第四次移位后:2→3→4,回到起点;
可以发现:他的位置以“3,1,2,4,”循环出现,
2019÷4=504…3,
所以第2019次移位后他的编号与第三次相同,到达编号为2的点;
故选:B.
二.填空题(共6小题,满分18分,每小题3分)
13.解:∵该立体图形上面和底面都是三角形,且有三条棱,
∴它的名称是三棱柱,
故答案为:三棱柱.
14.解:∵﹣ x2m﹣3y4与3x5yn+2的和仍是单项式,
∴﹣x2m﹣3y4与3x5yn+2是同类项.
∴2m﹣3=5,n+2=4.
解得:m=4,n=2.
∴mn=8.
故答案为:8.
15.解:∵|a|=5,
∴a=±5,
∵b=﹣3,a+b>0,
∴a=5,
∴ab=5×(﹣3)=﹣15,
故答案为﹣15.
16.解:如图所示,
∵当x=﹣1时,1+x﹣2x2=1﹣1﹣2=﹣2>﹣5,
∴输入x=﹣2,
∴1+x﹣2x2=1﹣2﹣8=﹣9<﹣5,
∴输出的结果为﹣9.
故答案为﹣9.
17.解:根据题意得:2x﹣+x=,
去分母得:4x﹣1+2x=3,
解得:x=.
故答案为:
18.解:∵进价为a元/台的体育健身器材,提价60%后的标价为:(1 十60%)a=1.6a元,
∴打八折优惠后的售价为:
0.8(1+60%)a=0.8 x 1.6a=1.28a元,
∴每售出一台可获的利润为:1.28a﹣a=0.28a元,
故答案为:0.28a.
三.解答题(共7小题,满分66分)
19.解:(1)原式=3a2b﹣ab2+ab2+5a2b=8a2b,
当a=2,b=﹣1时,原式=8×22×(﹣1)=﹣32;
(2)∵a,b互为相反数,c,d互为倒数,m的绝对值是3,
∴a+b=0,cd=1,m=3或﹣3,
当m=3时,原式=0+3﹣1=2;
当m=﹣3时,原式=0﹣3﹣1=﹣4,
则原式的值为2或﹣4.
20.解:(1)去括号得:2x﹣2=2﹣5x﹣10,
移项得:2x+5x=2﹣10+2,
合并得:7x=﹣6,
解得:x=﹣;
(2)去分母得:2(5x+1)﹣(7x+2)=4,
去括号得:10x+2﹣7x﹣2=4,
移项得:10x﹣7x=4﹣2+2,
合并得:3x=4,
解得:x=.
21.解:∵CD=AD=BC,
∴AD=4CD,BC=6CD,
则AC=3CD,BD=5CD,AB=9CD;
∵点E、F分别为线段AC,BD的中点,
∴EC=AC=CD,DF=BD=CD;
∵EF=5cm,
∴EF=EC+CD+DF=CD+CD+CD=5CD,
∴CD=1cm,
∴AB=9CD=9×1=9(cm).
22.解:(1)设经销A品牌轿车x辆,则经销B品牌轿车(50﹣x)辆,根据题意得
解这个不等式组得28≤x≤30
∴该公司经销这两种品牌轿车的方案有三种,即
方案一:经销A种品牌轿车28辆,B种品牌轿车22辆,
方案二:经销A种品牌轿车29辆,B种品牌轿车21辆,
方案三:经销A种品牌轿车30辆,B种品牌轿车20辆.
方案一获利(27﹣24)×28+(30﹣26)×22=172万元,
方案二获利(27﹣24)×29+(30﹣26)×21=171万元,
方案三获利(27﹣24)×30+(30﹣26)×20=170万元.
∴方案一获利最大,最大利润是172万元;
(2)方案一获利(a+3)×28+4×22=172+28a万元,
方案二获利(a+3)×29+4×21=171+29a万元,
方案三获利(a+3)×30+4×20=170+30a万元.
当0<a<1时,方案一获利最大,
当a=1时,三种方案获利一样大,
当1<a<1.2时,方案三获利最大.
23.解:(1)这次被调查的学生共有600÷60%=1000人,
故答案为:1000;
(2)剩少量的人数为1000﹣(600+150+50)=200人,
补全条形图如下:
(3),
答:估计该校18000名学生一餐浪费的食物可供900人食用一餐.
24.解:(1)窗户的面积是:
4a2+πa2÷2
=4a2+0.5πa2
=(4+0.5π)a2(cm2)
(2)窗户的外框的总长是:
2a×3+πa
=6a+πa
=(6+π)a(cm)
25.解:(1)设小明家离学校有x千米,根据题意得:
=+,
解得x=6,
答:小明家离学校有6千米;
(2)小明乘坐公共汽车上学需要6÷40=(小时).
同课章节目录
