2021-2022学年青岛版数学九年级上册期末练习试卷 (word版含解析)
文档属性
| 名称 | 2021-2022学年青岛版数学九年级上册期末练习试卷 (word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 192.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-17 12:28:21 | ||
图片预览



文档简介
2021-2022学年青岛新版九年级上学期数学期末练习试卷
一.选择题(共12小题,满分36分,每小题3分)
1.函数y=中自变量x的取值范围是( )
A.x>﹣3且x≠0 B.x≠0 C.x>﹣3 D.x≠﹣3或x≠0
2.在Rt△ABC中,∠C=90°,BC=1,AB=4,则sinB的值是( )
A. B. C. D.
3.把二次函数y=﹣x2﹣x+3用配方法化成y=a(x﹣h)2+k的形式时,应为( )
A.y=﹣(x﹣2)2+2 B.y=﹣(x﹣2)2+4
C.y=﹣(x+2)2+4 D.y=﹣(x﹣)2+3
4.在△ABC中,∠A,∠B都是锐角,若|sinA﹣|+(cosB﹣)2=0,则∠C的度数是( )
A.30° B.45° C.60° D.90°
5.如图,过⊙O上一点C作⊙O的切线,交⊙O直径AB的延长线于点D.若∠D=40°,则∠A的度数为( )
A.20° B.25° C.30° D.40°
6.若某等腰三角形的底边长和腰长是方程x2﹣6x+8=0的两实数根,则这个三角形的周长为( )
A.8 B.10 C.8或10 D.不能确定
7.如图,在直角坐标系中,直线AB经过点P(3,4),与坐标轴正半轴相交于A,B两点,当△AOB的面积最小时,△AOB的内切圆的半径是( )
A.2 B.3.5 C. D.4
8.圆心角为60°,半径为1的弧长为( )
A. B.π C. D.
9.关于x的一元二次方程﹣kx2﹣6x+3=0有两个不相等的实数根,则k的取值范围是( )
A.k>﹣3 B.k<3 C.k<3且k≠0 D.k>﹣3且k≠0
10.新冠肺炎传染性很强,曾有2人同时患上新冠肺炎,在一天内一人平均能传染x人,经过两天传染后128人患上新冠肺炎,则x的值为( )
A.10 B.9 C.8 D.7
11.将抛物线y=2x2平移得到抛物线y=2(x﹣2)2+3,下列平移正确的是( )
A.先向左平移2个单位,再向上平移3个单位
B.先向左平移2个单位,再向下平移3个单位
C.先向右平移2个单位,再向下平移3个单位
D.先向右平移2个单位,再向上平移3个单位
12.已知反比例函数y=,下列结论不正确的是( )
A.图象经过点(﹣2,1)
B.图象在第二、四象限
C.当x<0时,y随着x的增大而增大
D.当x>﹣1时,y>2
二.填空题(共5小题,满分15分,每小题3分)
13.方程3(x﹣4)=x(x﹣4)的解是 .
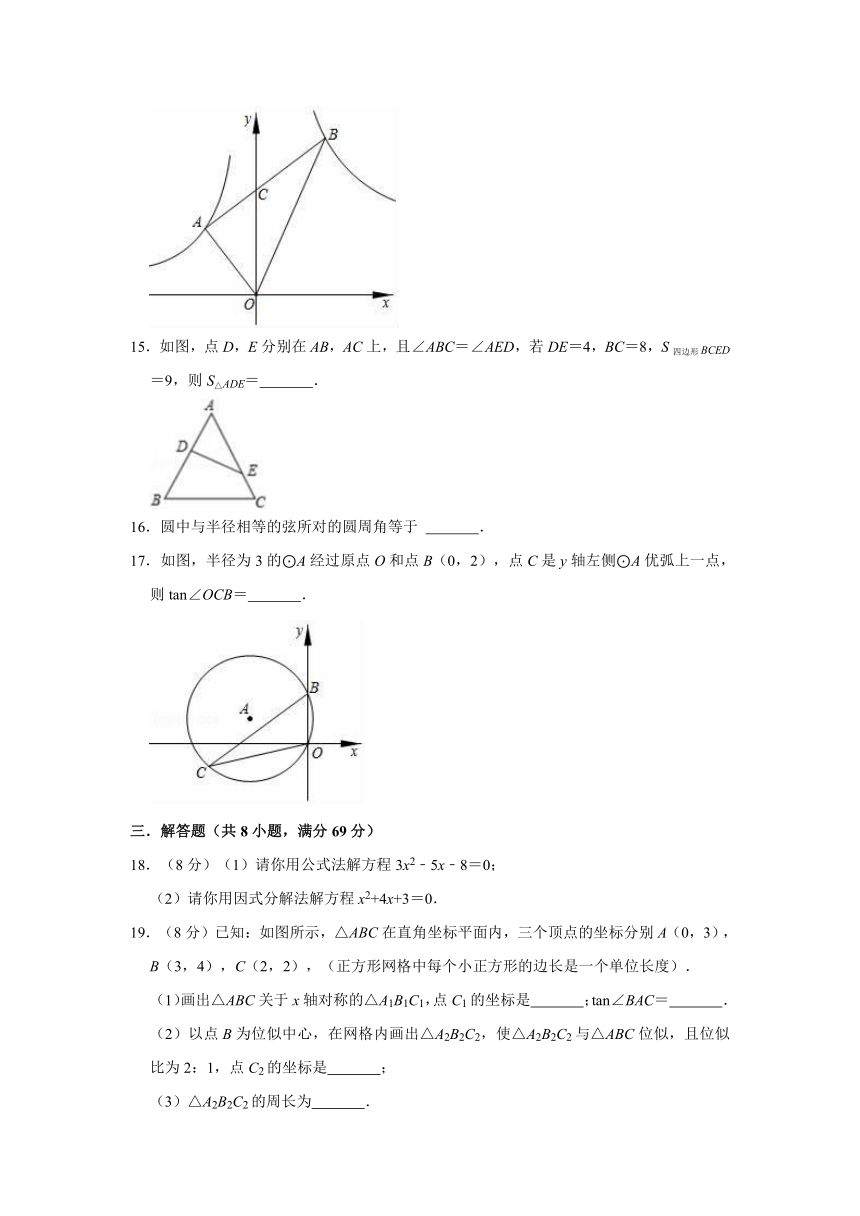
14.如图,Rt△AOB中,∠OAB=90°,∠OBA=30°,顶点A在反比例函数y=图象上,若Rt△AOB的面积恰好被y轴平分,则经过点B的反比例函数的解析式为 .
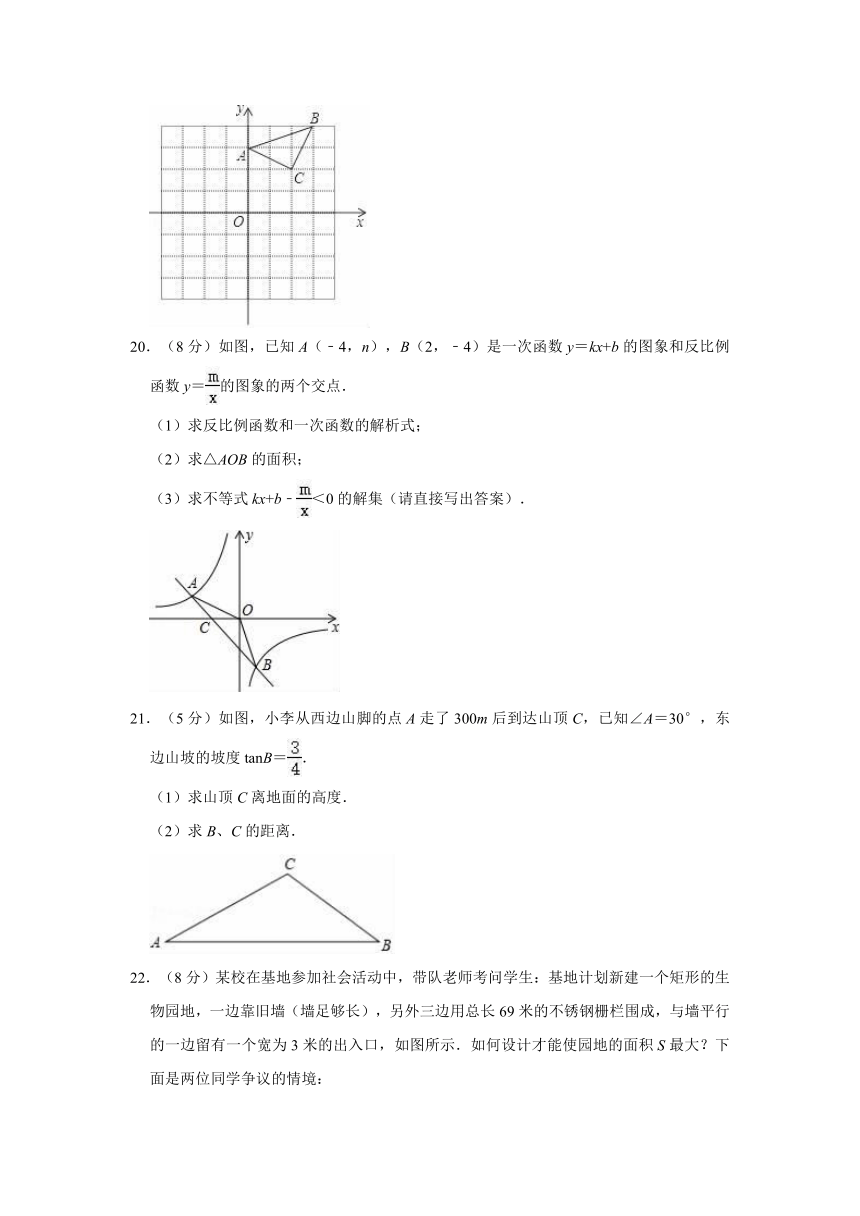
15.如图,点D,E分别在AB,AC上,且∠ABC=∠AED,若DE=4,BC=8,S四边形BCED=9,则S△ADE= .
16.圆中与半径相等的弦所对的圆周角等于 .
17.如图,半径为3的⊙A经过原点O和点B(0,2),点C是y轴左侧⊙A优弧上一点,则tan∠OCB= .
三.解答题(共8小题,满分69分)
18.(8分)(1)请你用公式法解方程3x2﹣5x﹣8=0;
(2)请你用因式分解法解方程x2+4x+3=0.
19.(8分)已知:如图所示,△ABC在直角坐标平面内,三个顶点的坐标分别A(0,3),B(3,4),C(2,2),(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC关于x轴对称的△A1B1C1,点C1的坐标是 ;tan∠BAC= .
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 ;
(3)△A2B2C2的周长为 .
20.(8分)如图,已知A(﹣4,n),B(2,﹣4)是一次函数y=kx+b的图象和反比例函数y=的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求△AOB的面积;
(3)求不等式kx+b﹣<0的解集(请直接写出答案).
21.(5分)如图,小李从西边山脚的点A走了300m后到达山顶C,已知∠A=30°,东边山坡的坡度tanB=.
(1)求山顶C离地面的高度.
(2)求B、C的距离.
22.(8分)某校在基地参加社会活动中,带队老师考问学生:基地计划新建一个矩形的生物园地,一边靠旧墙(墙足够长),另外三边用总长69米的不锈钢栅栏围成,与墙平行的一边留有一个宽为3米的出入口,如图所示.如何设计才能使园地的面积S最大?下面是两位同学争议的情境:
小军:把它围成一个正方形,这样的面积一定最大.
小英:不对啦!面积最大的不是正方形.
请根据上面信息,解决问题:
(1)设AB=x米(x>0).
①BC= 米(用含x的代数式表示);
②x的取值范围是 ;
(2)请你判断谁的说法正确,为什么?
23.(10分)广安市某楼盘准备以每平方米6000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,房地产开发商为了加快资金周转,对价格经过两次下调后,决定以每平方米4860元的均价开盘销售.
(1)求平均每次下调的百分率.
(2)某人准备以开盘价均价购买一套100平方米的住房,开发商给予以下两种优惠方案以供选择:①打9.8折销售;②不打折,一次性送装修费每平方米80元,试问哪种方案更优惠?
24.(10分)如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC,AC于点D,E,DG⊥AC于点G,交AB的延长线于点F.
(1)求证:直线FG是⊙O的切线;
(2)若AC=10,cosA=,求CG的长.
25.(12分)如图,已知二次函数y=ax2+bx+3的图象过点A(﹣1,0),对称轴为过点(1,0)且与y轴平行的直线.
(1)求点B的坐标;
(2)求该二次函数的关系式;
(3)结合图象,解答下列问题:
①当x取什么值时,该函数的图象在x轴上方?
②当﹣1<x<2时,求函数y的取值范围.
参考答案与试题解析
一.选择题(共12小题,满分36分,每小题3分)
1.解:根据题意得到:x+3>0,
解得x>﹣3.
故选:C.
2.解:由勾股定理得,AC===
则sinB==,
故选:C.
3.解:y=﹣x2﹣x+3=﹣(x2+4x+4)+1+3=﹣(x+2)2+4.
故选:C.
4.解:∵∠A,∠B都是锐角,|sinA﹣|+(cosB﹣)2=0,
∴sinA=,cosB=,
∴∠A=30°,∠B=60°,
则∠C=180°﹣30°﹣60°=90°.
故选:D.
5.解:连接OC,
∵CD切⊙O于C,
∴OC⊥CD,
∴∠OCD=90°,
∵∠D=40°,
∴∠COD=180°﹣90°﹣40°=50°,
∵OA=OC,
∴∠A=∠OCA,
∵∠A+∠OCA=∠COD=50°,
∴∠A=25°.
故选:B.
6.解:∵x2﹣6x+8=0,
∴(x﹣2)(x﹣4)=0,
则x﹣2=0或x﹣4=0,
解得x1=2,x2=4,
若腰长为2,此时三角形三边长度分别为2、2、4,由2+2=4知不能构成三角形;
若腰长为4,此时三角形三边长度分别为4、4、2,符合三角形三边长度关系,
所以周长为4+4+2=10,
故选:B.
7.解:设直线AB的解析式是y=kx+b,
把P(3,4)代入得:4=3k+b,
b=4﹣3k,
即直线AB的解析式是y=kx+4﹣3k,
当x=0时,y=4﹣3k,
当y=0时,x=,
即A(0,4﹣3k),B(,0),
△AOB的面积是 OB OA= (4﹣3k)=12﹣=12﹣(k+),
∵要使△AOB的面积最小,
∴必须最大,
∵k<0,
∴﹣k>0,
∵(a﹣b)2≥0,
∴a2+b2≥2ab,
∴﹣k﹣≥2=12,
当且仅当﹣k=﹣时,取等号,解得:k=±,
∵k<0,
∴k=﹣,
即OA=4﹣3k=8,OB==6,
根据勾股定理得:AB==210,
设三角形AOB的内切圆的半径是R,
由三角形面积公式得:×6×8=×6R+×8R+×10R,
R=2,
故选:A.
8.解:圆心角为60°,半径为1的弧长==.
故选:D.
9.解:根据题意得﹣k≠0且Δ=(﹣6)2﹣4×(﹣k)×3>0,
解得k>﹣3且k≠0.
故选:D.
10.解:依题意得:2(1+x)2=128,
解得:x1=7,x2=﹣9(不合题意,舍去).
故选:D.
11.解:抛物线y=2x2的顶点坐标为(0,0),抛物线y=2(x﹣2)2+3的顶点坐标为(2,3),而点(0,0)先向右平移2个单位,再向上平移3个单位可得到点(2,3),
所以抛物线y=2x2先向右平移2个单位,再向上平移3个单位得到抛物线y=2(x﹣2)2+3.
故选:D.
12.解:A、把(﹣2,1)代入解析式得:左边=右边,故本选项正确,不符合题意;
B、因为﹣2<0,图象在第二、四象限,故本选项正确,不符合题意;
C、当x<0,且k<0,y随x的增大而增大,故本选项正确,不符合题意;
D、在第三象限时,当x>﹣1时,y>2,故本选项错误,符合题意.
故选:D.
二.填空题(共5小题,满分15分,每小题3分)
13.解:∵3(x﹣4)=x(x﹣4),
∴3(x﹣4)﹣x(x﹣4)=0,
则(x﹣4)(3﹣x)=0,
∴x﹣4=0或3﹣x=0,
解得x1=4,x2=3,
故答案为:x1=4,x2=3.
14.解:分别过A、B作AE⊥x轴于E,BD⊥y轴交AE于F.
∵顶点A在反比例函数y=图象上,
∴S△AOE=2.
∵∠OAB=90°,
∠OAE=90°﹣∠BAF=∠ABF,∠OEA=∠BFA=90°,
∴△OAE∽△ABF,
∴OA:AB=OE:AF=AE:BF,
在Rt△AOB中,∠AOAB=90°,∠OBA=30°,
∴OA:AB=1:,
∴=()2=3,
∵S△AOE=4=2,
∴S△ABF=6,
∴S△BCD=S△ABF=,
∵Rt△AOB的面积恰好被y轴平分,
∴AC=BC,
作AM∥OE交y轴于M,易证得△CDB≌△CMA,
∴S△CAM=
∴S△AOC=2+=,
∴S△BOC=S△AOC=,
∴S△BOD=+=5,
∴k=2S△BOD=10,
∴过点B的反比例函数的解析式为y=
故答案为:y=.
15.解:∵∠ABC=∠AED,∠DAE=∠CAB,
∴△ADE∽△ACB,
∴=()2=,
∴S△ADE:S四边形BCED=1:3,
∵S四边形BCED=9,
∴S△ADE=3.
故答案为:3.
16.解:根据题意弦所对的圆心角是60°,
∴它所对的优弧上的圆周角=×60°=30°,
劣弧上的圆周角=180°﹣30°=150°.
故应填30°或150°.
17.解:设⊙A交x轴于A,连接BD,则BD是直径,
在Rt△OBD中,BD=6,OB=2,
则OD==4,
tan∠BDO==,
由圆周角定理得,∠OCB=∠BDO,
则tan∠OCB=,
故答案为:.
三.解答题(共8小题,满分69分)
18.解:(1)∵a=3,b=﹣5,c=﹣8,
∴Δ=(﹣5)2﹣4×3×(﹣8)=121>0,
则x==,
∴x1=,x2=﹣1;
(2)∵x2+4x+3=0,
∴(x+1)(x+3)=0,
∴x+1=0或x+3=0,
解得x1=﹣1,x2=﹣3.
19.解:(1)如图,△A1B1C1为所作,点C1的坐标是(2,﹣2),tan∠BAC=1,
故答案为(2,﹣2),1;
(2)如图,△A2B2C2为所作,点C2的坐标为(1,0),
故答案为(1,0);
(3)△A2B2C2的周长=A2C2+B2C2+A2B2=++=4+2
故答案为4+2.
20.解:(1)把B(2,﹣4)代入y=得m=2×(﹣4)=﹣8,
所以反比例函数解析式为y=﹣,
把A(﹣4,n)代入y=﹣得﹣4n=﹣8,解得n=2,则A点坐标为(﹣4,2),
把A(﹣4,2)、B(2,﹣4)代入y=kx+b得,解得,
所以一次函数解析式为y=﹣x﹣2;
(2)把y=0代入y=﹣x﹣2得﹣x﹣2=0,解得x=﹣2,则C点坐标为(﹣2,0),
所以S△AOB=S△AOC+S△BOC=×2×2+×2×4=6;
(3)﹣4<x<0或x>2.
21.解:(1)过点C作CD⊥AB于D,
在Rt△ACD中,∠A=30°,AC=300m,
∴CD=AC=150(m),
答:山顶C离地面的高度为150m;
(2)在Rt△BCD中,tanB=,
∴=,即=,
解得,BD=200(m),
由勾股定理得,BC==250(m),
答:B、C的距离为250m.
22.解:(1)①由题意得:69+3﹣2x=72﹣2x.
故答案为:72﹣2x.
②由题意得:69﹣2x≥0,
解得:x≤34.5,
∴0<x≤34.5,
故答案为:0<x≤34.5;
(2)小英的说法正确,理由是:
∵S=x(72﹣2x)
=﹣2x2+72x
=﹣2(x﹣18)2+648,
又∵x=18在0<x≤34.5范围内,
∴当x=18时,面积S最大,
此时AB=CD=18,而BC=72﹣2×18=36,
∴四边形ABCD不是正方形,
∴小英的说法正确.
23.解:(1)设平均每次下调的百分率为x,
则6000(1﹣x)2=4860,
解得:x1=0.1=10%,x2=1.9(舍去),
故平均每次下调的百分率为10%;
(2)方案①购房优惠:4860×100×(1﹣0.98)=9720(元);
方案②可优惠:80×100=8000(元).
故选择方案①更优惠.
24.(1)证明:如图,连接OD,,
∵AB=AC,
∴∠C=∠ABC,
∵OD=OB,
∴∠ABC=∠ODB,
∴∠ODB=∠C,
∴OD∥AC,
∴∠ODG=∠DGC,
∵DG⊥AC,
∴∠DGC=90°,
∴∠ODG=90°,
∴OD⊥FG,
∵OD是⊙O的半径,
∴直线FG是⊙O的切线.
(2)解:如图,,
∵AB=AC=10,AB是⊙O的直径,
∴OA=OD=10÷2=5,
由(1),可得
OD⊥FG,OD∥AC,
∴∠ODF=90°,∠DOF=∠A,
在△ODF和△AGF中,
∴△ODF∽△AGF,
∴,
∵cosA=,
∴cos∠DOF=,
∴=,
∴AF=AO+OF=5,
∴,
解得AG=7,
∴CG=AC﹣AG=10﹣7=3,
即CG的长是3.
25.解:(1)∵函数图象与x轴的一个交点坐标为A(﹣1,0),且对称轴为直线x=1,
∴函数图象与x轴的另一个交点为(3,0);
(2)根据题意可得:,
解得:,
则二次函数解析式为y=﹣x2+2x+3=﹣(x﹣1)2+4;
(3)①当﹣1<x<3 时,该函数的图象在x轴上方;
②∵函数的顶点坐标为(1,4),
∴当x=1时,y的最大值为4,
∴当﹣1<x<2时,函数y的取值范围为0<y≤4.
一.选择题(共12小题,满分36分,每小题3分)
1.函数y=中自变量x的取值范围是( )
A.x>﹣3且x≠0 B.x≠0 C.x>﹣3 D.x≠﹣3或x≠0
2.在Rt△ABC中,∠C=90°,BC=1,AB=4,则sinB的值是( )
A. B. C. D.
3.把二次函数y=﹣x2﹣x+3用配方法化成y=a(x﹣h)2+k的形式时,应为( )
A.y=﹣(x﹣2)2+2 B.y=﹣(x﹣2)2+4
C.y=﹣(x+2)2+4 D.y=﹣(x﹣)2+3
4.在△ABC中,∠A,∠B都是锐角,若|sinA﹣|+(cosB﹣)2=0,则∠C的度数是( )
A.30° B.45° C.60° D.90°
5.如图,过⊙O上一点C作⊙O的切线,交⊙O直径AB的延长线于点D.若∠D=40°,则∠A的度数为( )
A.20° B.25° C.30° D.40°
6.若某等腰三角形的底边长和腰长是方程x2﹣6x+8=0的两实数根,则这个三角形的周长为( )
A.8 B.10 C.8或10 D.不能确定
7.如图,在直角坐标系中,直线AB经过点P(3,4),与坐标轴正半轴相交于A,B两点,当△AOB的面积最小时,△AOB的内切圆的半径是( )
A.2 B.3.5 C. D.4
8.圆心角为60°,半径为1的弧长为( )
A. B.π C. D.
9.关于x的一元二次方程﹣kx2﹣6x+3=0有两个不相等的实数根,则k的取值范围是( )
A.k>﹣3 B.k<3 C.k<3且k≠0 D.k>﹣3且k≠0
10.新冠肺炎传染性很强,曾有2人同时患上新冠肺炎,在一天内一人平均能传染x人,经过两天传染后128人患上新冠肺炎,则x的值为( )
A.10 B.9 C.8 D.7
11.将抛物线y=2x2平移得到抛物线y=2(x﹣2)2+3,下列平移正确的是( )
A.先向左平移2个单位,再向上平移3个单位
B.先向左平移2个单位,再向下平移3个单位
C.先向右平移2个单位,再向下平移3个单位
D.先向右平移2个单位,再向上平移3个单位
12.已知反比例函数y=,下列结论不正确的是( )
A.图象经过点(﹣2,1)
B.图象在第二、四象限
C.当x<0时,y随着x的增大而增大
D.当x>﹣1时,y>2
二.填空题(共5小题,满分15分,每小题3分)
13.方程3(x﹣4)=x(x﹣4)的解是 .
14.如图,Rt△AOB中,∠OAB=90°,∠OBA=30°,顶点A在反比例函数y=图象上,若Rt△AOB的面积恰好被y轴平分,则经过点B的反比例函数的解析式为 .
15.如图,点D,E分别在AB,AC上,且∠ABC=∠AED,若DE=4,BC=8,S四边形BCED=9,则S△ADE= .
16.圆中与半径相等的弦所对的圆周角等于 .
17.如图,半径为3的⊙A经过原点O和点B(0,2),点C是y轴左侧⊙A优弧上一点,则tan∠OCB= .
三.解答题(共8小题,满分69分)
18.(8分)(1)请你用公式法解方程3x2﹣5x﹣8=0;
(2)请你用因式分解法解方程x2+4x+3=0.
19.(8分)已知:如图所示,△ABC在直角坐标平面内,三个顶点的坐标分别A(0,3),B(3,4),C(2,2),(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC关于x轴对称的△A1B1C1,点C1的坐标是 ;tan∠BAC= .
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 ;
(3)△A2B2C2的周长为 .
20.(8分)如图,已知A(﹣4,n),B(2,﹣4)是一次函数y=kx+b的图象和反比例函数y=的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求△AOB的面积;
(3)求不等式kx+b﹣<0的解集(请直接写出答案).
21.(5分)如图,小李从西边山脚的点A走了300m后到达山顶C,已知∠A=30°,东边山坡的坡度tanB=.
(1)求山顶C离地面的高度.
(2)求B、C的距离.
22.(8分)某校在基地参加社会活动中,带队老师考问学生:基地计划新建一个矩形的生物园地,一边靠旧墙(墙足够长),另外三边用总长69米的不锈钢栅栏围成,与墙平行的一边留有一个宽为3米的出入口,如图所示.如何设计才能使园地的面积S最大?下面是两位同学争议的情境:
小军:把它围成一个正方形,这样的面积一定最大.
小英:不对啦!面积最大的不是正方形.
请根据上面信息,解决问题:
(1)设AB=x米(x>0).
①BC= 米(用含x的代数式表示);
②x的取值范围是 ;
(2)请你判断谁的说法正确,为什么?
23.(10分)广安市某楼盘准备以每平方米6000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,房地产开发商为了加快资金周转,对价格经过两次下调后,决定以每平方米4860元的均价开盘销售.
(1)求平均每次下调的百分率.
(2)某人准备以开盘价均价购买一套100平方米的住房,开发商给予以下两种优惠方案以供选择:①打9.8折销售;②不打折,一次性送装修费每平方米80元,试问哪种方案更优惠?
24.(10分)如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC,AC于点D,E,DG⊥AC于点G,交AB的延长线于点F.
(1)求证:直线FG是⊙O的切线;
(2)若AC=10,cosA=,求CG的长.
25.(12分)如图,已知二次函数y=ax2+bx+3的图象过点A(﹣1,0),对称轴为过点(1,0)且与y轴平行的直线.
(1)求点B的坐标;
(2)求该二次函数的关系式;
(3)结合图象,解答下列问题:
①当x取什么值时,该函数的图象在x轴上方?
②当﹣1<x<2时,求函数y的取值范围.
参考答案与试题解析
一.选择题(共12小题,满分36分,每小题3分)
1.解:根据题意得到:x+3>0,
解得x>﹣3.
故选:C.
2.解:由勾股定理得,AC===
则sinB==,
故选:C.
3.解:y=﹣x2﹣x+3=﹣(x2+4x+4)+1+3=﹣(x+2)2+4.
故选:C.
4.解:∵∠A,∠B都是锐角,|sinA﹣|+(cosB﹣)2=0,
∴sinA=,cosB=,
∴∠A=30°,∠B=60°,
则∠C=180°﹣30°﹣60°=90°.
故选:D.
5.解:连接OC,
∵CD切⊙O于C,
∴OC⊥CD,
∴∠OCD=90°,
∵∠D=40°,
∴∠COD=180°﹣90°﹣40°=50°,
∵OA=OC,
∴∠A=∠OCA,
∵∠A+∠OCA=∠COD=50°,
∴∠A=25°.
故选:B.
6.解:∵x2﹣6x+8=0,
∴(x﹣2)(x﹣4)=0,
则x﹣2=0或x﹣4=0,
解得x1=2,x2=4,
若腰长为2,此时三角形三边长度分别为2、2、4,由2+2=4知不能构成三角形;
若腰长为4,此时三角形三边长度分别为4、4、2,符合三角形三边长度关系,
所以周长为4+4+2=10,
故选:B.
7.解:设直线AB的解析式是y=kx+b,
把P(3,4)代入得:4=3k+b,
b=4﹣3k,
即直线AB的解析式是y=kx+4﹣3k,
当x=0时,y=4﹣3k,
当y=0时,x=,
即A(0,4﹣3k),B(,0),
△AOB的面积是 OB OA= (4﹣3k)=12﹣=12﹣(k+),
∵要使△AOB的面积最小,
∴必须最大,
∵k<0,
∴﹣k>0,
∵(a﹣b)2≥0,
∴a2+b2≥2ab,
∴﹣k﹣≥2=12,
当且仅当﹣k=﹣时,取等号,解得:k=±,
∵k<0,
∴k=﹣,
即OA=4﹣3k=8,OB==6,
根据勾股定理得:AB==210,
设三角形AOB的内切圆的半径是R,
由三角形面积公式得:×6×8=×6R+×8R+×10R,
R=2,
故选:A.
8.解:圆心角为60°,半径为1的弧长==.
故选:D.
9.解:根据题意得﹣k≠0且Δ=(﹣6)2﹣4×(﹣k)×3>0,
解得k>﹣3且k≠0.
故选:D.
10.解:依题意得:2(1+x)2=128,
解得:x1=7,x2=﹣9(不合题意,舍去).
故选:D.
11.解:抛物线y=2x2的顶点坐标为(0,0),抛物线y=2(x﹣2)2+3的顶点坐标为(2,3),而点(0,0)先向右平移2个单位,再向上平移3个单位可得到点(2,3),
所以抛物线y=2x2先向右平移2个单位,再向上平移3个单位得到抛物线y=2(x﹣2)2+3.
故选:D.
12.解:A、把(﹣2,1)代入解析式得:左边=右边,故本选项正确,不符合题意;
B、因为﹣2<0,图象在第二、四象限,故本选项正确,不符合题意;
C、当x<0,且k<0,y随x的增大而增大,故本选项正确,不符合题意;
D、在第三象限时,当x>﹣1时,y>2,故本选项错误,符合题意.
故选:D.
二.填空题(共5小题,满分15分,每小题3分)
13.解:∵3(x﹣4)=x(x﹣4),
∴3(x﹣4)﹣x(x﹣4)=0,
则(x﹣4)(3﹣x)=0,
∴x﹣4=0或3﹣x=0,
解得x1=4,x2=3,
故答案为:x1=4,x2=3.
14.解:分别过A、B作AE⊥x轴于E,BD⊥y轴交AE于F.
∵顶点A在反比例函数y=图象上,
∴S△AOE=2.
∵∠OAB=90°,
∠OAE=90°﹣∠BAF=∠ABF,∠OEA=∠BFA=90°,
∴△OAE∽△ABF,
∴OA:AB=OE:AF=AE:BF,
在Rt△AOB中,∠AOAB=90°,∠OBA=30°,
∴OA:AB=1:,
∴=()2=3,
∵S△AOE=4=2,
∴S△ABF=6,
∴S△BCD=S△ABF=,
∵Rt△AOB的面积恰好被y轴平分,
∴AC=BC,
作AM∥OE交y轴于M,易证得△CDB≌△CMA,
∴S△CAM=
∴S△AOC=2+=,
∴S△BOC=S△AOC=,
∴S△BOD=+=5,
∴k=2S△BOD=10,
∴过点B的反比例函数的解析式为y=
故答案为:y=.
15.解:∵∠ABC=∠AED,∠DAE=∠CAB,
∴△ADE∽△ACB,
∴=()2=,
∴S△ADE:S四边形BCED=1:3,
∵S四边形BCED=9,
∴S△ADE=3.
故答案为:3.
16.解:根据题意弦所对的圆心角是60°,
∴它所对的优弧上的圆周角=×60°=30°,
劣弧上的圆周角=180°﹣30°=150°.
故应填30°或150°.
17.解:设⊙A交x轴于A,连接BD,则BD是直径,
在Rt△OBD中,BD=6,OB=2,
则OD==4,
tan∠BDO==,
由圆周角定理得,∠OCB=∠BDO,
则tan∠OCB=,
故答案为:.
三.解答题(共8小题,满分69分)
18.解:(1)∵a=3,b=﹣5,c=﹣8,
∴Δ=(﹣5)2﹣4×3×(﹣8)=121>0,
则x==,
∴x1=,x2=﹣1;
(2)∵x2+4x+3=0,
∴(x+1)(x+3)=0,
∴x+1=0或x+3=0,
解得x1=﹣1,x2=﹣3.
19.解:(1)如图,△A1B1C1为所作,点C1的坐标是(2,﹣2),tan∠BAC=1,
故答案为(2,﹣2),1;
(2)如图,△A2B2C2为所作,点C2的坐标为(1,0),
故答案为(1,0);
(3)△A2B2C2的周长=A2C2+B2C2+A2B2=++=4+2
故答案为4+2.
20.解:(1)把B(2,﹣4)代入y=得m=2×(﹣4)=﹣8,
所以反比例函数解析式为y=﹣,
把A(﹣4,n)代入y=﹣得﹣4n=﹣8,解得n=2,则A点坐标为(﹣4,2),
把A(﹣4,2)、B(2,﹣4)代入y=kx+b得,解得,
所以一次函数解析式为y=﹣x﹣2;
(2)把y=0代入y=﹣x﹣2得﹣x﹣2=0,解得x=﹣2,则C点坐标为(﹣2,0),
所以S△AOB=S△AOC+S△BOC=×2×2+×2×4=6;
(3)﹣4<x<0或x>2.
21.解:(1)过点C作CD⊥AB于D,
在Rt△ACD中,∠A=30°,AC=300m,
∴CD=AC=150(m),
答:山顶C离地面的高度为150m;
(2)在Rt△BCD中,tanB=,
∴=,即=,
解得,BD=200(m),
由勾股定理得,BC==250(m),
答:B、C的距离为250m.
22.解:(1)①由题意得:69+3﹣2x=72﹣2x.
故答案为:72﹣2x.
②由题意得:69﹣2x≥0,
解得:x≤34.5,
∴0<x≤34.5,
故答案为:0<x≤34.5;
(2)小英的说法正确,理由是:
∵S=x(72﹣2x)
=﹣2x2+72x
=﹣2(x﹣18)2+648,
又∵x=18在0<x≤34.5范围内,
∴当x=18时,面积S最大,
此时AB=CD=18,而BC=72﹣2×18=36,
∴四边形ABCD不是正方形,
∴小英的说法正确.
23.解:(1)设平均每次下调的百分率为x,
则6000(1﹣x)2=4860,
解得:x1=0.1=10%,x2=1.9(舍去),
故平均每次下调的百分率为10%;
(2)方案①购房优惠:4860×100×(1﹣0.98)=9720(元);
方案②可优惠:80×100=8000(元).
故选择方案①更优惠.
24.(1)证明:如图,连接OD,,
∵AB=AC,
∴∠C=∠ABC,
∵OD=OB,
∴∠ABC=∠ODB,
∴∠ODB=∠C,
∴OD∥AC,
∴∠ODG=∠DGC,
∵DG⊥AC,
∴∠DGC=90°,
∴∠ODG=90°,
∴OD⊥FG,
∵OD是⊙O的半径,
∴直线FG是⊙O的切线.
(2)解:如图,,
∵AB=AC=10,AB是⊙O的直径,
∴OA=OD=10÷2=5,
由(1),可得
OD⊥FG,OD∥AC,
∴∠ODF=90°,∠DOF=∠A,
在△ODF和△AGF中,
∴△ODF∽△AGF,
∴,
∵cosA=,
∴cos∠DOF=,
∴=,
∴AF=AO+OF=5,
∴,
解得AG=7,
∴CG=AC﹣AG=10﹣7=3,
即CG的长是3.
25.解:(1)∵函数图象与x轴的一个交点坐标为A(﹣1,0),且对称轴为直线x=1,
∴函数图象与x轴的另一个交点为(3,0);
(2)根据题意可得:,
解得:,
则二次函数解析式为y=﹣x2+2x+3=﹣(x﹣1)2+4;
(3)①当﹣1<x<3 时,该函数的图象在x轴上方;
②∵函数的顶点坐标为(1,4),
∴当x=1时,y的最大值为4,
∴当﹣1<x<2时,函数y的取值范围为0<y≤4.
同课章节目录
