2021-2022学年人教版八年级数学上册13.1轴对称 同步练习(word版、含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学上册13.1轴对称 同步练习(word版、含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 442.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-17 00:00:00 | ||
图片预览



文档简介
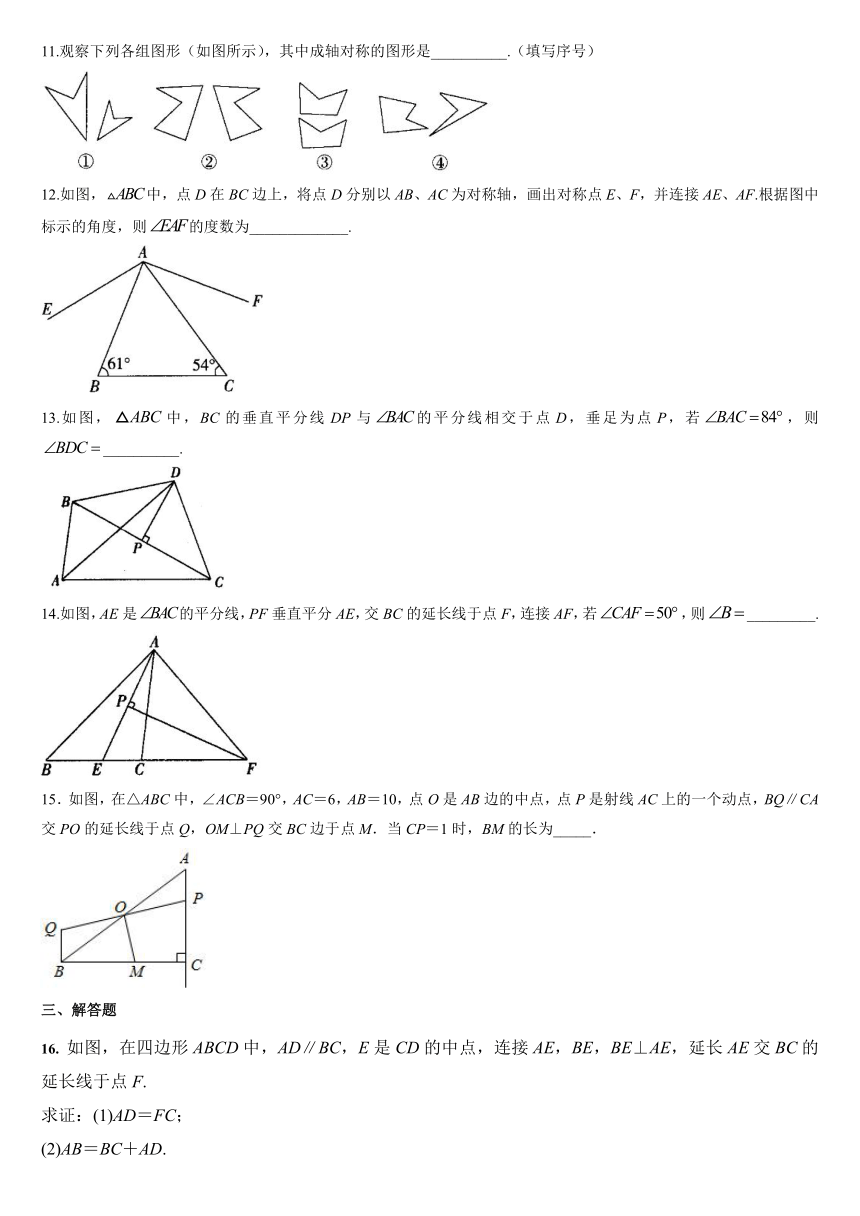
第十三章轴对称 13.1轴对称
一、选择题
1.C、D是线段的垂直平分线上的两点,平分,则下列说法不一定正确的是( ).
A. B. C.垂直平分 D.
2.如图,线段、关于直线成轴对称,点、分别在、上,且.、相交于点.图中关于成轴对称的三角形共有( )
A.1对 B.2对 C.3对 D.4对
3.下列图形中,是轴对称图形的是( )
A. B. C. D.
4.如图是北京大兴国际机场俯视图的示意图.下列说法正确的是( )
A.这个图形是轴对称图形,但不是中心对称图形
B.这个图形是中心对称图形,但不是轴对称图形
C.这个图形既是轴对称图形,又是中心对称图形
D.这个图形既不是轴对称图形,也不是中心对称图形
5.如图,△ABC与△A′B′C′关于直线l对称,且∠A=78°,∠C′=48°,则∠B的度数为( )
A.48° B.54° C.64° D.78°
6.如图所示,在△ABC中,内角∠BAC与外角∠CBE的平分线相交于点P,,PGAD交BC于F,交AB于G,①;②S△PAC:S△PAB=PC:PB;③BP垂直平分CE;④∠PCF=∠CPF.其中正确的有( )
A.①②④ B.①③④ C.②③④ D.①③
7.如图,在锐角三角形中,,按以下步骤作图:①以点为圆心,长为半径作圆弧,交于点;②分别以点A、为圆心,大于长为半径作圆弧,计两弧交于点;③作射线,交于点,若,则的大小为( )
A. B. C. D.
8.如图,△ABC中,C、C′关于AB对称,B、B′关于AC对称,D、E分别在AB、AC上,且C′D∥BC∥B′E,BE,CD交于点F,若∠BFD=α,∠BAC=β,则α与β之间的关系为( )
A.2β+α=180° B.α=2β C.α= D.α=180°﹣
9.如图,在四边形ABCD中,ABDC,E为BC的中点,连接DE、AE,AE⊥DE,延长DE交AB的延长线于点F.若AB=5,CD=3,则AD的长为( )
A.2 B.5 C.8 D.11
10.如图,中,的平分线与边的垂直平分线相交于交的延长线于于F,现有下列结论:①;②;③平分;④若,则.其中正确的个数为( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.观察下列各组图形(如图所示),其中成轴对称的图形是__________.(填写序号)
12.如图,中,点D在BC边上,将点D分别以AB、AC为对称轴,画出对称点E、F,并连接AE、AF.根据图中标示的角度,则的度数为_____________.
13.如图,中,BC的垂直平分线DP与的平分线相交于点D,垂足为点P,若,则__________.
14.如图,AE是的平分线,PF垂直平分AE,交BC的延长线于点F,连接AF,若,则_________.
15.如图,在△ABC中,∠ACB=90°,AC=6,AB=10,点O是AB边的中点,点P是射线AC上的一个动点,BQ∥CA交PO的延长线于点Q,OM⊥PQ交BC边于点M.当CP=1时,BM的长为_____.
三、解答题
16. 如图,在四边形ABCD中,AD∥BC,E是CD的中点,连接AE,BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)AD=FC;
(2)AB=BC+AD.
17. 如图,在△ABC中,AB边的垂直平分线DE分别与AB边和AC边交于点D和点E,BC边的垂直平分线FG分别与BC边和AC边交于点F和点G,若△BEG的周长为16,GE=3,求AC的长.
18. 已知:如图,∠BAC的平分线与BC的垂直平分线DG交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F.
(1)求证:BE=CF;
(2)若AF=6,BC=7,求△ABC的周长.
19.综合与探究
在数学综合实践课上,老师让同学用两张全等的等腰三角形纸片进行拼摆,并探究摆放后所构成的图形之间的关系.如图1,△ABC≌△DEF,AB=AC,DE=DF.
[探究一]
(1)勤奋小组的同学把这两张纸片按如图2的方式摆放,点A与点D重合,连接BE和CF.他们发现BE与CF之间存在着一定的数量关系,这个关系是 .
[探究二](2)创新小组的同学在勤奋小组的启发下,把这两张纸片按如图3的方式摆放,点F,A,D,C在同一直线上,连接BF和CE,他们发现了BF和CE之间的数量和位置关系,请写出这些关系并说明理由;
[探究三](3)从A,B两题中任选一题作答.解答时用尺规作△DEF,不写作法,保留作图痕迹.
A.如图4,利用△ABC纸片拼摆出一种与图2和图3都不相同的图形,并根据图形写出一个数学结论.
B.如图4,利用△ABC纸片拼摆出一种与图2和图3都不相同的图形,并根据图形提出一个数学问题并解答.
【参考答案】
1.D 2.D 3.D 4.A 5.B 6.B 7.C 8.B 9.C 10.C
11.答案:②
解析:找成轴对称的图形的关键是寻找对称轴,成轴对称的两个图形沿对称轴折叠后可完全重合.
12.答案:130°
解析:连接AD,如图.
点D分别以AB、AC为对称轴,对称点为E、F,,,,;,.
13.答案:96°
解析:如图,过点D作,交AB的延长线于点E,于点F, AD平分,, DP垂直平分BC,.
在和中,
.,,,,,.
14.答案:50°
解析:直线PF垂直平分AE,,,又,,.由AE平分,得,.
15.2.5或1
16. 【答案】
证明:(1)∵E是CD的中点,∴DE=CE.
∵AD∥BC,
∴∠ADE=∠FCE,∠DAE=∠CFE.
∴△ADE≌△FCE.∴AD=FC.
(2)∵△ADE≌△FCE,
∴AE=FE.
又∵BE⊥AE,∴BE垂直平分AF.
∴AB=FB.
∵FB=BC+FC=BC+AD,
∴AB=BC+AD.
17. 【答案】
解:∵DE垂直平分线段AB,GF垂直平分线段BC,
∴EB=EA,GB=GC.
∵△BEG的周长为16,
∴EB+GB+GE=16.
∴EA+GC+GE=16.
∴GA+GE+GE+GE+EC=16.
∴AC+2GE=16.
∵GE=3,
∴AC=10.
18. 【答案】
(1)证明:如图,连接CD.
∵点D在BC的垂直平分线上,∴BD=CD.
∵DE⊥AB,DF⊥AC,AD平分∠BAC,
∴DE=DF,∠BED=∠CFD=90°.
在Rt△BDE和Rt△CDF中,
∴Rt△BDE≌Rt△CDF(HL).∴BE=CF.
(2)在Rt△ADE和Rt△ADF中,
∴Rt△ADE≌Rt△ADF.
∴AE=AF=6.
∴△ABC的周长=AB+BC+AC=(AE+BE)+BC+(AF-CF)=6+7+6=19.
19.解:(1)如图2,BE=CF,理由如下:
∵△ABC≌△DEF,
∴∠BAC=∠EDF,
∴∠BAC+∠CAE=∠EDF+∠EAF,即∠BAE=∠CDF,
在△BAE和△CDF中
∴△BAE≌△CDF(SAS),
∴BE=CF;
故答案为BE=CF;
(2)如图3,BF=CE,BF∥CE,理由如下:
∵△ABC≌△DEF,
∴∠BAC=∠EDF,AC=DF,AB=DE,
∴∠BAF=∠EDC,AF=DC
在△ABF和△DEC中
∴△ABF≌△DEC(SAS),
∴BF=CE,∠AFB=∠DCE,
∴BF∥CE;
(3)A、如图:把这两张纸片按如图方式摆放,AC与DF重合,
根据题意可知:∠DAE=∠ADB
∴AE∥BC;
B、如图:
把这两张纸片按如图方式摆放,BC与EF重合,请写出AD和BC的位置关系并注明;
解答:AD垂直平分BC,
证明:∵AB=AC,DE=DF.
∴AD垂直平分BC.
一、选择题
1.C、D是线段的垂直平分线上的两点,平分,则下列说法不一定正确的是( ).
A. B. C.垂直平分 D.
2.如图,线段、关于直线成轴对称,点、分别在、上,且.、相交于点.图中关于成轴对称的三角形共有( )
A.1对 B.2对 C.3对 D.4对
3.下列图形中,是轴对称图形的是( )
A. B. C. D.
4.如图是北京大兴国际机场俯视图的示意图.下列说法正确的是( )
A.这个图形是轴对称图形,但不是中心对称图形
B.这个图形是中心对称图形,但不是轴对称图形
C.这个图形既是轴对称图形,又是中心对称图形
D.这个图形既不是轴对称图形,也不是中心对称图形
5.如图,△ABC与△A′B′C′关于直线l对称,且∠A=78°,∠C′=48°,则∠B的度数为( )
A.48° B.54° C.64° D.78°
6.如图所示,在△ABC中,内角∠BAC与外角∠CBE的平分线相交于点P,,PGAD交BC于F,交AB于G,①;②S△PAC:S△PAB=PC:PB;③BP垂直平分CE;④∠PCF=∠CPF.其中正确的有( )
A.①②④ B.①③④ C.②③④ D.①③
7.如图,在锐角三角形中,,按以下步骤作图:①以点为圆心,长为半径作圆弧,交于点;②分别以点A、为圆心,大于长为半径作圆弧,计两弧交于点;③作射线,交于点,若,则的大小为( )
A. B. C. D.
8.如图,△ABC中,C、C′关于AB对称,B、B′关于AC对称,D、E分别在AB、AC上,且C′D∥BC∥B′E,BE,CD交于点F,若∠BFD=α,∠BAC=β,则α与β之间的关系为( )
A.2β+α=180° B.α=2β C.α= D.α=180°﹣
9.如图,在四边形ABCD中,ABDC,E为BC的中点,连接DE、AE,AE⊥DE,延长DE交AB的延长线于点F.若AB=5,CD=3,则AD的长为( )
A.2 B.5 C.8 D.11
10.如图,中,的平分线与边的垂直平分线相交于交的延长线于于F,现有下列结论:①;②;③平分;④若,则.其中正确的个数为( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.观察下列各组图形(如图所示),其中成轴对称的图形是__________.(填写序号)
12.如图,中,点D在BC边上,将点D分别以AB、AC为对称轴,画出对称点E、F,并连接AE、AF.根据图中标示的角度,则的度数为_____________.
13.如图,中,BC的垂直平分线DP与的平分线相交于点D,垂足为点P,若,则__________.
14.如图,AE是的平分线,PF垂直平分AE,交BC的延长线于点F,连接AF,若,则_________.
15.如图,在△ABC中,∠ACB=90°,AC=6,AB=10,点O是AB边的中点,点P是射线AC上的一个动点,BQ∥CA交PO的延长线于点Q,OM⊥PQ交BC边于点M.当CP=1时,BM的长为_____.
三、解答题
16. 如图,在四边形ABCD中,AD∥BC,E是CD的中点,连接AE,BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)AD=FC;
(2)AB=BC+AD.
17. 如图,在△ABC中,AB边的垂直平分线DE分别与AB边和AC边交于点D和点E,BC边的垂直平分线FG分别与BC边和AC边交于点F和点G,若△BEG的周长为16,GE=3,求AC的长.
18. 已知:如图,∠BAC的平分线与BC的垂直平分线DG交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F.
(1)求证:BE=CF;
(2)若AF=6,BC=7,求△ABC的周长.
19.综合与探究
在数学综合实践课上,老师让同学用两张全等的等腰三角形纸片进行拼摆,并探究摆放后所构成的图形之间的关系.如图1,△ABC≌△DEF,AB=AC,DE=DF.
[探究一]
(1)勤奋小组的同学把这两张纸片按如图2的方式摆放,点A与点D重合,连接BE和CF.他们发现BE与CF之间存在着一定的数量关系,这个关系是 .
[探究二](2)创新小组的同学在勤奋小组的启发下,把这两张纸片按如图3的方式摆放,点F,A,D,C在同一直线上,连接BF和CE,他们发现了BF和CE之间的数量和位置关系,请写出这些关系并说明理由;
[探究三](3)从A,B两题中任选一题作答.解答时用尺规作△DEF,不写作法,保留作图痕迹.
A.如图4,利用△ABC纸片拼摆出一种与图2和图3都不相同的图形,并根据图形写出一个数学结论.
B.如图4,利用△ABC纸片拼摆出一种与图2和图3都不相同的图形,并根据图形提出一个数学问题并解答.
【参考答案】
1.D 2.D 3.D 4.A 5.B 6.B 7.C 8.B 9.C 10.C
11.答案:②
解析:找成轴对称的图形的关键是寻找对称轴,成轴对称的两个图形沿对称轴折叠后可完全重合.
12.答案:130°
解析:连接AD,如图.
点D分别以AB、AC为对称轴,对称点为E、F,,,,;,.
13.答案:96°
解析:如图,过点D作,交AB的延长线于点E,于点F, AD平分,, DP垂直平分BC,.
在和中,
.,,,,,.
14.答案:50°
解析:直线PF垂直平分AE,,,又,,.由AE平分,得,.
15.2.5或1
16. 【答案】
证明:(1)∵E是CD的中点,∴DE=CE.
∵AD∥BC,
∴∠ADE=∠FCE,∠DAE=∠CFE.
∴△ADE≌△FCE.∴AD=FC.
(2)∵△ADE≌△FCE,
∴AE=FE.
又∵BE⊥AE,∴BE垂直平分AF.
∴AB=FB.
∵FB=BC+FC=BC+AD,
∴AB=BC+AD.
17. 【答案】
解:∵DE垂直平分线段AB,GF垂直平分线段BC,
∴EB=EA,GB=GC.
∵△BEG的周长为16,
∴EB+GB+GE=16.
∴EA+GC+GE=16.
∴GA+GE+GE+GE+EC=16.
∴AC+2GE=16.
∵GE=3,
∴AC=10.
18. 【答案】
(1)证明:如图,连接CD.
∵点D在BC的垂直平分线上,∴BD=CD.
∵DE⊥AB,DF⊥AC,AD平分∠BAC,
∴DE=DF,∠BED=∠CFD=90°.
在Rt△BDE和Rt△CDF中,
∴Rt△BDE≌Rt△CDF(HL).∴BE=CF.
(2)在Rt△ADE和Rt△ADF中,
∴Rt△ADE≌Rt△ADF.
∴AE=AF=6.
∴△ABC的周长=AB+BC+AC=(AE+BE)+BC+(AF-CF)=6+7+6=19.
19.解:(1)如图2,BE=CF,理由如下:
∵△ABC≌△DEF,
∴∠BAC=∠EDF,
∴∠BAC+∠CAE=∠EDF+∠EAF,即∠BAE=∠CDF,
在△BAE和△CDF中
∴△BAE≌△CDF(SAS),
∴BE=CF;
故答案为BE=CF;
(2)如图3,BF=CE,BF∥CE,理由如下:
∵△ABC≌△DEF,
∴∠BAC=∠EDF,AC=DF,AB=DE,
∴∠BAF=∠EDC,AF=DC
在△ABF和△DEC中
∴△ABF≌△DEC(SAS),
∴BF=CE,∠AFB=∠DCE,
∴BF∥CE;
(3)A、如图:把这两张纸片按如图方式摆放,AC与DF重合,
根据题意可知:∠DAE=∠ADB
∴AE∥BC;
B、如图:
把这两张纸片按如图方式摆放,BC与EF重合,请写出AD和BC的位置关系并注明;
解答:AD垂直平分BC,
证明:∵AB=AC,DE=DF.
∴AD垂直平分BC.
