2021-2022学年高二上学期数学人教A版(2019)选择性必修第二册4.4.2等差数列的前项和公式(第一课时)课件(共37张PPT)
文档属性
| 名称 | 2021-2022学年高二上学期数学人教A版(2019)选择性必修第二册4.4.2等差数列的前项和公式(第一课时)课件(共37张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-18 00:00:00 | ||
图片预览








文档简介
(共37张PPT)
(第一课时)
等差数列的前n项和公式
回顾:等差系列公式
1. 等差数列定义:
2. 等差数列通项公式:
(2) an=am+(n-m)d .
(3) an=pn+q (p、q是常数)
(1) an=a1+(n-1)d (n≥1).
an-an-1 =d (n≥2)
或 an+1-an =d.
18
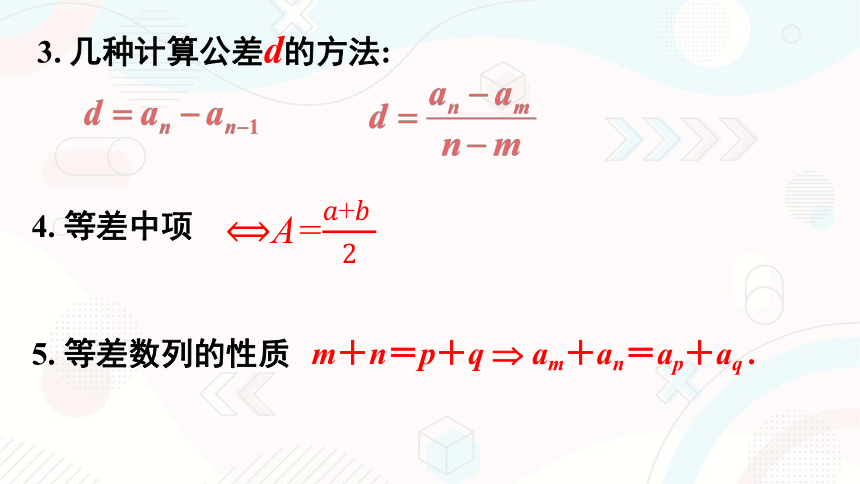
3. 几种计算公差d的方法:
4. 等差中项
A=
m+n=p+q am+an=ap+aq .
5. 等差数列的性质
泰姬陵坐落于印度古都阿格,是十七世纪莫卧儿帝国皇帝沙杰罕为纪念其爱妃所建,她宏伟壮观,纯白大理石砌建而成的主体建筑叫人心醉神迷,成为世界七大奇迹之一。陵寝以宝石镶饰,图案之细致令人叫绝.
传说陵寝中有一个三角形图案,以相同大小的圆宝石镶饰而成,共有100层(见左图),奢靡之程度,可见一斑。你知道这个图案一共花了多少宝石吗?
1+2+3+···+100 = ?
“数学王子”高斯的开挂人生
据说,二百多年前,高斯的算术老师提出了下面问题:1+2+3+...+100=
当其他同学忙于把100个数逐项相加时,10岁的高斯却用下面的方法迅速算出了正确答案:
情境导入
高斯(Gauss ,1777-1855),德国著名数学家、物理学家、天文学家,
近代数学奠基者之一,并享有"数学王子"之称.
他和阿基米德、牛顿、
欧拉并列为世界四大数学家.
以他名字“高斯”命名的成果
达110个,属数学家中之最.
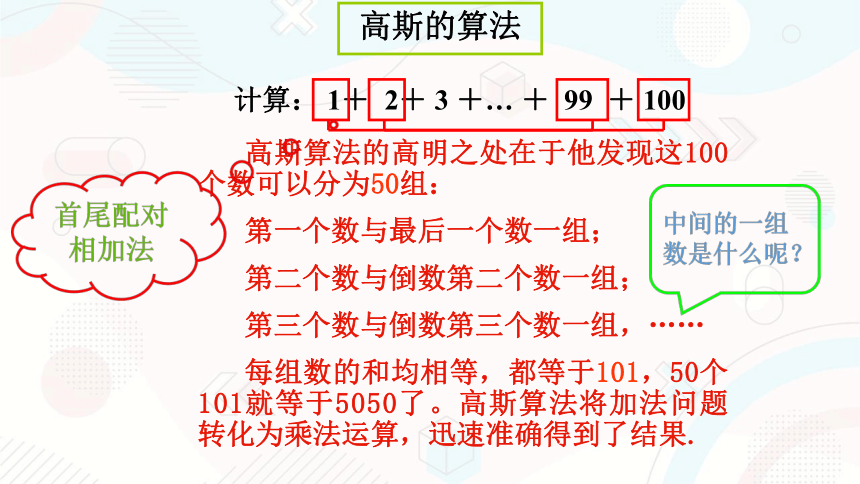
高斯的算法
计算: 1+ 2+ 3 +… + 99 + 100
高斯算法的高明之处在于他发现这100个数可以分为50组:
第一个数与最后一个数一组;
第二个数与倒数第二个数一组;
第三个数与倒数第三个数一组,……
每组数的和均相等,都等于101,50个101就等于5050了。高斯算法将加法问题转化为乘法运算,迅速准确得到了结果.
问题:你能说说高斯在求和过程中利用了数列的什么性质吗?
,那么高斯的计算方法可以表示为
可以发现,高斯在计算中利用了
===这一特殊关系.
追问:高斯的方法妙在哪里?
相同数(即101)的求和
简化运算
不同数的
求和问题
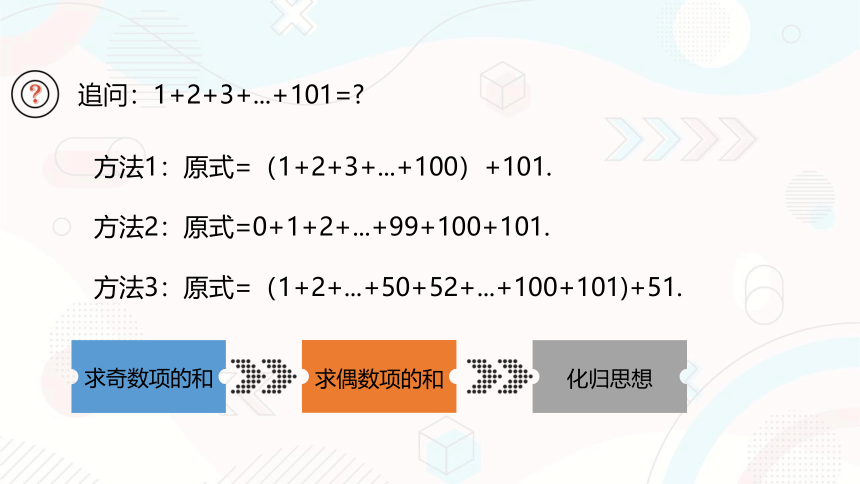
追问:1+2+3+...+101=
方法1:原式=(1+2+3+...+100)+101.
方法2:原式=0+1+2+...+99+100+101.
方法3:原式=(1+2+...+50+52+...+100+101)+51.
求偶数项的和
化归思想
求奇数项的和
能否设法避免分类讨论?
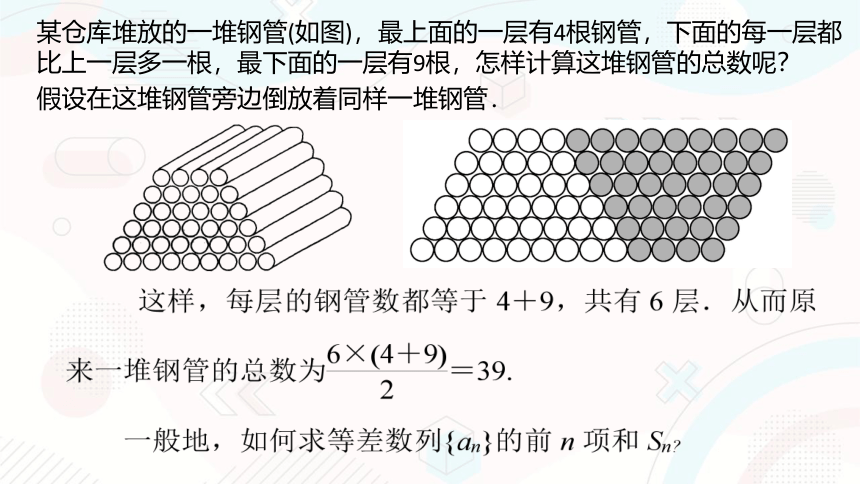
某仓库堆放的一堆钢管(如图),最上面的一层有4根钢管,下面的每一层都比上一层多一根,最下面的一层有9根,怎样计算这堆钢管的总数呢?
假设在这堆钢管旁边倒放着同样一堆钢管.
解:S100=1+2+3+ … +98+99+100 (1)
S100=100+99+98+ … +3+ 2+1 (2)
2S100=(1+100) ×100,
(1)+(2)得
问题: 求 S100=1+ 2+3+ … +98+99+100
动脑思考 探索新知
n + (n-1) + (n-2) +…+ 2 +1
倒序相加法
那么,对一般的等差数列,如何求它的前n项和呢?
①
②
问题分析
已知等差数列{ an }的首项为a1,项数是n,第n项为an,求前n项和Sn .
①
②
追问:把等差数列的通项公式代入公式(1),可以得到什么?
(2)
追问:不从公式(1)出发,你能用其他方法得到公式(2)吗?
Sn =a1 +a2 + a3 +…+ an-1 +an
+
这个公式表明,等差数列的前n项和可由首项、公差和项数唯一确定.
等差数列的前项和n公式:
如果等差数列{an}的首项a1,公差为d ,那么该等差数列的前n项和公式为:
等差数列的通项公式和前n项和公式中,共有“a1,d ,n,an,Sn”五个量,故知三可求其二.
如何根据公式的结构特征来记忆公式呢?
等腰梯形的面积=平行四边形面积+三角形面积
求和公式
两个公式的共同点是需知 a1和 n,不同点是前者还需知 an,后者还需知 d,解题时需根据已知条件决定选用哪个公式。
已知等差数列的前n项和为Sn,且a1=3,公差d=2,则 S5=( )
A.30 B.35 C.40 D.45
例6 已知数列{an}是等差数列.
(1)若a1=7,a50=101,求S50; (2)若a1=2,a2=,求S10;
(3)若a1=,d=-, Sn =-5,求n.
解: (1)
(2) --2=
+d
2+
例6 已知数列{an}是等差数列.
(1)若a1=7,a50=101,求S50; (2)若a1=2,a2=,求S10;
(3)若a1=,d=-, Sn =-5,求n.
解: (3)+d,得
n+
整理,得
-7n-60=0
解得
n=12或n=-5(舍去)
所以
n=12
课本P22 练习 1
1.根据下列各题中的条件,求相应等差数列的前n项和Sn.
(1)a1=5, an=95, n=10; (2)a1=100, d=-2, n=50;
(3)a1=-4, a8=-18, n=10; (4)a1=14.5, d=0.7, an=32.
课本P23 练习 2
2.等差数列-1,-3,-5,…的前多少项的和是-100
解:由于S10=310,S20=1220,将它们代入公式
可得
所以
例7 已知一个等差数列的前10项和是310,前 20项和是1220,求该数列的前n项和.
另解:
两式相减得
例7 已知一个等差数列的前10项和是310,前 20项和是1220,求该数列的前n项和.
课本P23 练习 3
3.在等差数列中,Sn为其前n项的和,若S4=6,S8=20,求S16.
在等差数列中,Sn为的前n项和,若S4=1,S8=4,则a17+a18+a19+a20的值为( )
A.9 B.12 C.16 D.18
等差数列中,a2+a7+a12=24,则的前13项和 S13=______________.
(2021年四川月考)等差数列的前项和为Sn,若a4,a10是方程x2-8x+1=0的两根,则S13= ( )
A.58 B.54 C.52 D.56
若等差数列的前5项和S5=25且a2=3,则a7等于( )
A.12 B.13 C.14 D.15
课本P23 练习 4
4.在等差数列中,若S15=5(a2+a6+ak),求k.
设Sn是等差数列的前n项和,若则
A.1 B. -1 C.2 D.
观察
例:如果等差数列的前4项和是4,前9项和是-6求前n项和的公式 。
解:令
应用知识 强化练习
说明:两个等差数列的求和公式及通项公式,一共涉及到 5 个量,通常已知其中 3 个,可求另外 2 个.
本小节结束
(第一课时)
等差数列的前n项和公式
回顾:等差系列公式
1. 等差数列定义:
2. 等差数列通项公式:
(2) an=am+(n-m)d .
(3) an=pn+q (p、q是常数)
(1) an=a1+(n-1)d (n≥1).
an-an-1 =d (n≥2)
或 an+1-an =d.
18
3. 几种计算公差d的方法:
4. 等差中项
A=
m+n=p+q am+an=ap+aq .
5. 等差数列的性质
泰姬陵坐落于印度古都阿格,是十七世纪莫卧儿帝国皇帝沙杰罕为纪念其爱妃所建,她宏伟壮观,纯白大理石砌建而成的主体建筑叫人心醉神迷,成为世界七大奇迹之一。陵寝以宝石镶饰,图案之细致令人叫绝.
传说陵寝中有一个三角形图案,以相同大小的圆宝石镶饰而成,共有100层(见左图),奢靡之程度,可见一斑。你知道这个图案一共花了多少宝石吗?
1+2+3+···+100 = ?
“数学王子”高斯的开挂人生
据说,二百多年前,高斯的算术老师提出了下面问题:1+2+3+...+100=
当其他同学忙于把100个数逐项相加时,10岁的高斯却用下面的方法迅速算出了正确答案:
情境导入
高斯(Gauss ,1777-1855),德国著名数学家、物理学家、天文学家,
近代数学奠基者之一,并享有"数学王子"之称.
他和阿基米德、牛顿、
欧拉并列为世界四大数学家.
以他名字“高斯”命名的成果
达110个,属数学家中之最.
高斯的算法
计算: 1+ 2+ 3 +… + 99 + 100
高斯算法的高明之处在于他发现这100个数可以分为50组:
第一个数与最后一个数一组;
第二个数与倒数第二个数一组;
第三个数与倒数第三个数一组,……
每组数的和均相等,都等于101,50个101就等于5050了。高斯算法将加法问题转化为乘法运算,迅速准确得到了结果.
问题:你能说说高斯在求和过程中利用了数列的什么性质吗?
,那么高斯的计算方法可以表示为
可以发现,高斯在计算中利用了
===这一特殊关系.
追问:高斯的方法妙在哪里?
相同数(即101)的求和
简化运算
不同数的
求和问题
追问:1+2+3+...+101=
方法1:原式=(1+2+3+...+100)+101.
方法2:原式=0+1+2+...+99+100+101.
方法3:原式=(1+2+...+50+52+...+100+101)+51.
求偶数项的和
化归思想
求奇数项的和
能否设法避免分类讨论?
某仓库堆放的一堆钢管(如图),最上面的一层有4根钢管,下面的每一层都比上一层多一根,最下面的一层有9根,怎样计算这堆钢管的总数呢?
假设在这堆钢管旁边倒放着同样一堆钢管.
解:S100=1+2+3+ … +98+99+100 (1)
S100=100+99+98+ … +3+ 2+1 (2)
2S100=(1+100) ×100,
(1)+(2)得
问题: 求 S100=1+ 2+3+ … +98+99+100
动脑思考 探索新知
n + (n-1) + (n-2) +…+ 2 +1
倒序相加法
那么,对一般的等差数列,如何求它的前n项和呢?
①
②
问题分析
已知等差数列{ an }的首项为a1,项数是n,第n项为an,求前n项和Sn .
①
②
追问:把等差数列的通项公式代入公式(1),可以得到什么?
(2)
追问:不从公式(1)出发,你能用其他方法得到公式(2)吗?
Sn =a1 +a2 + a3 +…+ an-1 +an
+
这个公式表明,等差数列的前n项和可由首项、公差和项数唯一确定.
等差数列的前项和n公式:
如果等差数列{an}的首项a1,公差为d ,那么该等差数列的前n项和公式为:
等差数列的通项公式和前n项和公式中,共有“a1,d ,n,an,Sn”五个量,故知三可求其二.
如何根据公式的结构特征来记忆公式呢?
等腰梯形的面积=平行四边形面积+三角形面积
求和公式
两个公式的共同点是需知 a1和 n,不同点是前者还需知 an,后者还需知 d,解题时需根据已知条件决定选用哪个公式。
已知等差数列的前n项和为Sn,且a1=3,公差d=2,则 S5=( )
A.30 B.35 C.40 D.45
例6 已知数列{an}是等差数列.
(1)若a1=7,a50=101,求S50; (2)若a1=2,a2=,求S10;
(3)若a1=,d=-, Sn =-5,求n.
解: (1)
(2) --2=
+d
2+
例6 已知数列{an}是等差数列.
(1)若a1=7,a50=101,求S50; (2)若a1=2,a2=,求S10;
(3)若a1=,d=-, Sn =-5,求n.
解: (3)+d,得
n+
整理,得
-7n-60=0
解得
n=12或n=-5(舍去)
所以
n=12
课本P22 练习 1
1.根据下列各题中的条件,求相应等差数列的前n项和Sn.
(1)a1=5, an=95, n=10; (2)a1=100, d=-2, n=50;
(3)a1=-4, a8=-18, n=10; (4)a1=14.5, d=0.7, an=32.
课本P23 练习 2
2.等差数列-1,-3,-5,…的前多少项的和是-100
解:由于S10=310,S20=1220,将它们代入公式
可得
所以
例7 已知一个等差数列的前10项和是310,前 20项和是1220,求该数列的前n项和.
另解:
两式相减得
例7 已知一个等差数列的前10项和是310,前 20项和是1220,求该数列的前n项和.
课本P23 练习 3
3.在等差数列中,Sn为其前n项的和,若S4=6,S8=20,求S16.
在等差数列中,Sn为的前n项和,若S4=1,S8=4,则a17+a18+a19+a20的值为( )
A.9 B.12 C.16 D.18
等差数列中,a2+a7+a12=24,则的前13项和 S13=______________.
(2021年四川月考)等差数列的前项和为Sn,若a4,a10是方程x2-8x+1=0的两根,则S13= ( )
A.58 B.54 C.52 D.56
若等差数列的前5项和S5=25且a2=3,则a7等于( )
A.12 B.13 C.14 D.15
课本P23 练习 4
4.在等差数列中,若S15=5(a2+a6+ak),求k.
设Sn是等差数列的前n项和,若则
A.1 B. -1 C.2 D.
观察
例:如果等差数列的前4项和是4,前9项和是-6求前n项和的公式 。
解:令
应用知识 强化练习
说明:两个等差数列的求和公式及通项公式,一共涉及到 5 个量,通常已知其中 3 个,可求另外 2 个.
本小节结束
