10.5 带电粒子在电场中的运动(Word版含答案)
文档属性
| 名称 | 10.5 带电粒子在电场中的运动(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 156.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
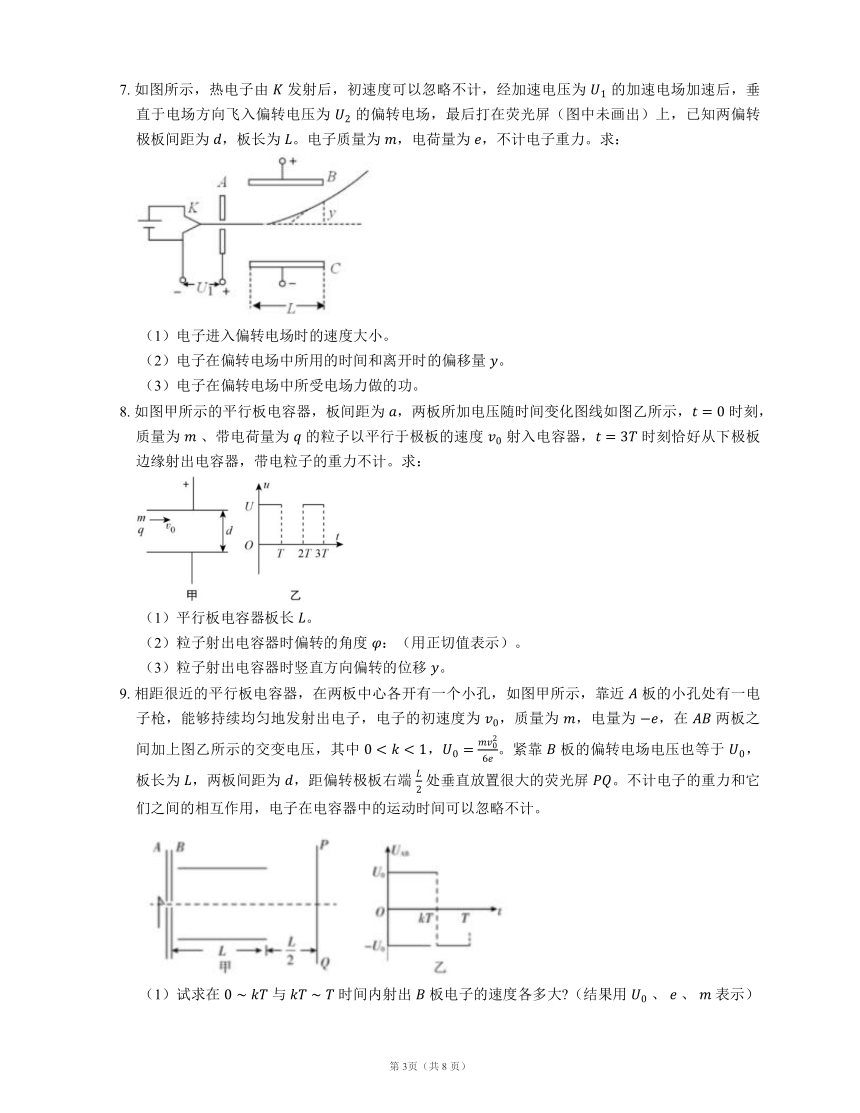
| 科目 | 物理 | ||
| 更新时间 | 2022-01-17 14:22:56 | ||
图片预览



文档简介
10.5 带电粒子在电场中的运动 能力
一、单项选择题(共5小题;共20分)
1. 如图所示,电子在电势差为 的加速电场中由静止开始运动,然后射入电势差为 的两块平行极板间的匀强电场中,入射方向跟极板平行。整个装置处在真空中,电子所受重力可忽略。在满足电子能射出平行板区域的条件下,下述四种情况中,一定能使电子的偏转角 变大的是
A. 变大、 变大 B. 变小、 变大
C. 变大、 变小 D. 变小、 变小
2. 如图()所示的两平行金属板 、 间加上图()所示电压, 时, 板电势比 板高 ,在两板正中央 点放一电子,初速度为零,电子只受静电力而运动,且不会碰到金属板,则这个电子处于 点右侧、速度向右,且速度逐渐减小的时间段是
A. B.
C. D.
3. 如图所示,加速电场的两极板间距为 ,两极板间电压为 ,偏转电场的平行金属板的板长 ,两极板电压为 ,设一初速度为零的带电粒子经加速电场加速后,沿两板中线垂直进入偏转电场中,带电粒子离开偏转电场后打在距离偏转电场为 的屏上,当偏转电场无电压时,带电粒子恰好击中荧光屏上的中心点 ,当偏转电场加上偏转电压 时,打在荧光屏上的 点,在满足粒子能射出偏转电场的条件下,不计重力影响,下列说法正确的是
A. 若使 增加一倍,则粒子在偏转电场中的运动时间减少一半
B. 若使 增加一倍,则粒子打在屏上的位置 到 的距离增加一倍
C. 若使 增加一倍,则粒子打在屏上时的速度大小增加一倍
D. 若使 增加一倍,则粒子在偏转电场中的运动时间减少一半
4. 如图甲所示,两平行正对的金属板 、 间加有如图乙所示的交变电压,一重力可忽略不计的带正电粒子被固定在两板的正中间 处。若在 时刻释放该粒子,粒子会时而向 板运动,时而向 板运动,并最终打在 板上。则 应满足
A. B. C. D.
5. 如图所示,在竖直放置的光滑半圆弧绝缘细管的圆心 处固定一点电荷,将质量为 ,带电量为 的小球从圆弧管的水平直径端点 由静止释放,小球沿细管滑到最低点 时,对管璧恰好无压力,则固定于圆心处的点电荷在 圆弧中点处的电场强度大小为
A. B. C. D.
二、双项选择题(共1小题;共4分)
6. 一带正电的小球向右水平抛入范围足够大的匀强电场,电场方向水平向左。不计空气阻力,则小球
A. 做直线运动 B. 做曲线运动
C. 速率先减小后增大 D. 速率先增大后减小
三、解答题(共3小题;共39分)
7. 如图所示,热电子由 发射后,初速度可以忽略不计,经加速电压为 的加速电场加速后,垂直于电场方向飞入偏转电压为 的偏转电场,最后打在荧光屏(图中未画出)上,已知两偏转极板间距为 ,板长为 。电子质量为 ,电荷量为 ,不计电子重力。求:
(1)电子进入偏转电场时的速度大小。
(2)电子在偏转电场中所用的时间和离开时的偏移量 。
(3)电子在偏转电场中所受电场力做的功。
8. 如图甲所示的平行板电容器,板间距为 ,两板所加电压随时间变化图线如图乙所示, 时刻,质量为 、带电荷量为 的粒子以平行于极板的速度 射入电容器, 时刻恰好从下极板边缘射出电容器,带电粒子的重力不计。求:
(1)平行板电容器板长 。
(2)粒子射出电容器时偏转的角度 :(用正切值表示)。
(3)粒子射出电容器时竖直方向偏转的位移 。
9. 相距很近的平行板电容器,在两板中心各开有一个小孔,如图甲所示,靠近 板的小孔处有一电子枪,能够持续均匀地发射出电子,电子的初速度为 ,质量为 ,电量为 ,在 两板之间加上图乙所示的交变电压,其中 ,。紧靠 板的偏转电场电压也等于 ,板长为 ,两板间距为 ,距偏转极板右端 处垂直放置很大的荧光屏 。不计电子的重力和它们之间的相互作用,电子在电容器中的运动时间可以忽略不计。
(1)试求在 与 时间内射出 板电子的速度各多大 (结果用 、 、 表示)
(2)在 时间内,荧光屏上有两个位置会发光,试求这两个发光点之间的距离。(结果用 、 表示)
(3)撤去偏转电场及荧光屏,当 取恰当的数值时,使在 时间内通过了电容器 板的所有电子,能在某一时刻形成均匀分布的一段电子束,求 值。
答案
第一部分
1. B
2. B
【解析】在 时间内, 板电势比 板高 ,所以电场方向水平向左,电子所受静电力方向向右,加速度方向也向右,所以电子从 点向右做匀加速直线运动,选项A错误;
在 时间内, 板电势比 板低 ,电场强度方向水平向右,所以电子所受静电力方向向左,加速度方向也向左,所以电子向右做匀减速直线运动,当 时速度为零,此时电子在 点的右侧,选项B正确;
在 时间内, 板电势比 板低 ,电场强度方向水平向右,所以电子所受静电力方向向左,加速度方向也向左,所以电子向左做匀加速直线运动,选项C错误;
在 时间内, 板电势比 板高 ,电场强度方向水平向左,所以电子所受静电力方向向右,加速度方向也向右,所以电子向左做匀减速直线运动,到 时刻速度为零,恰好又回到 点,选项D错误。
3. B
【解析】经历加速过程,由动能定理可得:,
解得:,
在偏转电场中的运动时间为:。
若使 增加一倍,则粒子在偏转电场中的运动时间不是减小一半,故A错误;运动时间与电压 没有关系,故D错误。
设偏转电场的板间距离为 ,偏转电场的场强: 则带电粒子所受的电场力:,
根据牛顿第二定律:
解得:,
带电粒子在偏转电场中做类平抛运动,竖直方向初速度为零的匀加速直线运动,所以:
;
竖直方向上的速度 ,
所以带电粒子离开偏转电场时的偏转角 的正切值为:,
,
所以:,
则:,
故若使 增加一倍,则粒子打在屏上的位置 到 的距离增加一倍,故B正确。
出电场后做匀速直线运动,击中屏的速度即为出电场时的速度,即:,若使 增加一倍,则粒子打在屏上时的速度大小不是增加一倍,故C错误。
4. B
【解析】若 ,带正电粒子先加速向 板运动,再减速运动至速度为零,然后反向加速运动,再减速运动至速度为零,如此往复运动,每次向右运动的距离大于向左运动的距离,最终打在 板上,选项A、C错误;若 ,带正电粒子先加速向 板运动,再减速运动至速度为零,然后反向加速运动,再减速运动至速度为零,如此往复运动,每次向左运动的距离大于向右运动的距离,最终打在 板上,选项B正确;若 ,带正电粒子先加速向 板运动,再减速运动至速度为零,然后反向加速运动,再减速运动至速度为零,如此往复运动,每次向左运动的距离小于向右运动的距离,最终打在 板上,选项D错误。
5. A
【解析】由题意知点电荷在 弧中点处的电场强度大小与圆弧中点 的场强大小相等,设为 ,则小球在该处受到的电场力为 ,
设小球至圆弧中点的速度为 ,圆弧半径为 ,如图所示:
对小球下滑至最低点的过程由机械能守恒定律得 ,
小球在圆弧中点根据题意,由牛顿第二定律得 ,
综合以上各式解得:。
第二部分
6. B, C
【解析】刚开始时带电小球所受重力与电场力的合力 跟 不在同一条直线上,所以它一定做曲线运动,A 项错误,B 项正确。因重力与电场力的合力 为恒力,结合图可知运动过程中合力 与速度之间的夹角由钝角减小到锐角,其中直角时速率最小,所以带电小球的速率先减小后增大,故 C 项正确,D 项错误。
第三部分
7. (1)
【解析】设电子加速后速度为 ,电子在加速电场中由动能定理得:
,
解得:。
(2)
【解析】在偏转电场中水平方向:,
竖直方向:,
解得:,
。
(3)
【解析】电子射出偏转电场的位置与射入偏转电场位置间的电压 ,
电场力所做的功 ,
解得:。
8. (1)
【解析】粒子水平方向做匀速运动:
。
(2)
【解析】粒子竖直方向先做 时间的匀加速运动,然后做 时间的匀速运动,再做 时间的匀加速运动:
,,。
(3)
【解析】竖直方向一共加速运动了 时间,匀速运动了 时间,
则 。
9. (1) ;
【解析】电子经过电容器内的电场后,速度要发生变化,设在 时间内,穿出 板后速度为 ,
时间内射出 板电子的速度 ,
据动能定理有:,,
将 代入上式,得 ,。
(2)
【解析】在 时间内射出板电子在偏转电场中,电子的运动时间:,侧移量: 得:
,
打在荧光屏上的坐标为 ,则:
,
同理可得在 时间内设穿出 板后电子侧移量:
,
打在荧光屏上的坐标:,
故两个发光点之间的距离:
。
(3)
【解析】要求在某一时刻形成均匀分布的一段电子束,前后两段电子束的长度必须相等(且刚好重叠),
第一束长度:,
第二束长度:,,
解得:。
第1页(共1 页)
一、单项选择题(共5小题;共20分)
1. 如图所示,电子在电势差为 的加速电场中由静止开始运动,然后射入电势差为 的两块平行极板间的匀强电场中,入射方向跟极板平行。整个装置处在真空中,电子所受重力可忽略。在满足电子能射出平行板区域的条件下,下述四种情况中,一定能使电子的偏转角 变大的是
A. 变大、 变大 B. 变小、 变大
C. 变大、 变小 D. 变小、 变小
2. 如图()所示的两平行金属板 、 间加上图()所示电压, 时, 板电势比 板高 ,在两板正中央 点放一电子,初速度为零,电子只受静电力而运动,且不会碰到金属板,则这个电子处于 点右侧、速度向右,且速度逐渐减小的时间段是
A. B.
C. D.
3. 如图所示,加速电场的两极板间距为 ,两极板间电压为 ,偏转电场的平行金属板的板长 ,两极板电压为 ,设一初速度为零的带电粒子经加速电场加速后,沿两板中线垂直进入偏转电场中,带电粒子离开偏转电场后打在距离偏转电场为 的屏上,当偏转电场无电压时,带电粒子恰好击中荧光屏上的中心点 ,当偏转电场加上偏转电压 时,打在荧光屏上的 点,在满足粒子能射出偏转电场的条件下,不计重力影响,下列说法正确的是
A. 若使 增加一倍,则粒子在偏转电场中的运动时间减少一半
B. 若使 增加一倍,则粒子打在屏上的位置 到 的距离增加一倍
C. 若使 增加一倍,则粒子打在屏上时的速度大小增加一倍
D. 若使 增加一倍,则粒子在偏转电场中的运动时间减少一半
4. 如图甲所示,两平行正对的金属板 、 间加有如图乙所示的交变电压,一重力可忽略不计的带正电粒子被固定在两板的正中间 处。若在 时刻释放该粒子,粒子会时而向 板运动,时而向 板运动,并最终打在 板上。则 应满足
A. B. C. D.
5. 如图所示,在竖直放置的光滑半圆弧绝缘细管的圆心 处固定一点电荷,将质量为 ,带电量为 的小球从圆弧管的水平直径端点 由静止释放,小球沿细管滑到最低点 时,对管璧恰好无压力,则固定于圆心处的点电荷在 圆弧中点处的电场强度大小为
A. B. C. D.
二、双项选择题(共1小题;共4分)
6. 一带正电的小球向右水平抛入范围足够大的匀强电场,电场方向水平向左。不计空气阻力,则小球
A. 做直线运动 B. 做曲线运动
C. 速率先减小后增大 D. 速率先增大后减小
三、解答题(共3小题;共39分)
7. 如图所示,热电子由 发射后,初速度可以忽略不计,经加速电压为 的加速电场加速后,垂直于电场方向飞入偏转电压为 的偏转电场,最后打在荧光屏(图中未画出)上,已知两偏转极板间距为 ,板长为 。电子质量为 ,电荷量为 ,不计电子重力。求:
(1)电子进入偏转电场时的速度大小。
(2)电子在偏转电场中所用的时间和离开时的偏移量 。
(3)电子在偏转电场中所受电场力做的功。
8. 如图甲所示的平行板电容器,板间距为 ,两板所加电压随时间变化图线如图乙所示, 时刻,质量为 、带电荷量为 的粒子以平行于极板的速度 射入电容器, 时刻恰好从下极板边缘射出电容器,带电粒子的重力不计。求:
(1)平行板电容器板长 。
(2)粒子射出电容器时偏转的角度 :(用正切值表示)。
(3)粒子射出电容器时竖直方向偏转的位移 。
9. 相距很近的平行板电容器,在两板中心各开有一个小孔,如图甲所示,靠近 板的小孔处有一电子枪,能够持续均匀地发射出电子,电子的初速度为 ,质量为 ,电量为 ,在 两板之间加上图乙所示的交变电压,其中 ,。紧靠 板的偏转电场电压也等于 ,板长为 ,两板间距为 ,距偏转极板右端 处垂直放置很大的荧光屏 。不计电子的重力和它们之间的相互作用,电子在电容器中的运动时间可以忽略不计。
(1)试求在 与 时间内射出 板电子的速度各多大 (结果用 、 、 表示)
(2)在 时间内,荧光屏上有两个位置会发光,试求这两个发光点之间的距离。(结果用 、 表示)
(3)撤去偏转电场及荧光屏,当 取恰当的数值时,使在 时间内通过了电容器 板的所有电子,能在某一时刻形成均匀分布的一段电子束,求 值。
答案
第一部分
1. B
2. B
【解析】在 时间内, 板电势比 板高 ,所以电场方向水平向左,电子所受静电力方向向右,加速度方向也向右,所以电子从 点向右做匀加速直线运动,选项A错误;
在 时间内, 板电势比 板低 ,电场强度方向水平向右,所以电子所受静电力方向向左,加速度方向也向左,所以电子向右做匀减速直线运动,当 时速度为零,此时电子在 点的右侧,选项B正确;
在 时间内, 板电势比 板低 ,电场强度方向水平向右,所以电子所受静电力方向向左,加速度方向也向左,所以电子向左做匀加速直线运动,选项C错误;
在 时间内, 板电势比 板高 ,电场强度方向水平向左,所以电子所受静电力方向向右,加速度方向也向右,所以电子向左做匀减速直线运动,到 时刻速度为零,恰好又回到 点,选项D错误。
3. B
【解析】经历加速过程,由动能定理可得:,
解得:,
在偏转电场中的运动时间为:。
若使 增加一倍,则粒子在偏转电场中的运动时间不是减小一半,故A错误;运动时间与电压 没有关系,故D错误。
设偏转电场的板间距离为 ,偏转电场的场强: 则带电粒子所受的电场力:,
根据牛顿第二定律:
解得:,
带电粒子在偏转电场中做类平抛运动,竖直方向初速度为零的匀加速直线运动,所以:
;
竖直方向上的速度 ,
所以带电粒子离开偏转电场时的偏转角 的正切值为:,
,
所以:,
则:,
故若使 增加一倍,则粒子打在屏上的位置 到 的距离增加一倍,故B正确。
出电场后做匀速直线运动,击中屏的速度即为出电场时的速度,即:,若使 增加一倍,则粒子打在屏上时的速度大小不是增加一倍,故C错误。
4. B
【解析】若 ,带正电粒子先加速向 板运动,再减速运动至速度为零,然后反向加速运动,再减速运动至速度为零,如此往复运动,每次向右运动的距离大于向左运动的距离,最终打在 板上,选项A、C错误;若 ,带正电粒子先加速向 板运动,再减速运动至速度为零,然后反向加速运动,再减速运动至速度为零,如此往复运动,每次向左运动的距离大于向右运动的距离,最终打在 板上,选项B正确;若 ,带正电粒子先加速向 板运动,再减速运动至速度为零,然后反向加速运动,再减速运动至速度为零,如此往复运动,每次向左运动的距离小于向右运动的距离,最终打在 板上,选项D错误。
5. A
【解析】由题意知点电荷在 弧中点处的电场强度大小与圆弧中点 的场强大小相等,设为 ,则小球在该处受到的电场力为 ,
设小球至圆弧中点的速度为 ,圆弧半径为 ,如图所示:
对小球下滑至最低点的过程由机械能守恒定律得 ,
小球在圆弧中点根据题意,由牛顿第二定律得 ,
综合以上各式解得:。
第二部分
6. B, C
【解析】刚开始时带电小球所受重力与电场力的合力 跟 不在同一条直线上,所以它一定做曲线运动,A 项错误,B 项正确。因重力与电场力的合力 为恒力,结合图可知运动过程中合力 与速度之间的夹角由钝角减小到锐角,其中直角时速率最小,所以带电小球的速率先减小后增大,故 C 项正确,D 项错误。
第三部分
7. (1)
【解析】设电子加速后速度为 ,电子在加速电场中由动能定理得:
,
解得:。
(2)
【解析】在偏转电场中水平方向:,
竖直方向:,
解得:,
。
(3)
【解析】电子射出偏转电场的位置与射入偏转电场位置间的电压 ,
电场力所做的功 ,
解得:。
8. (1)
【解析】粒子水平方向做匀速运动:
。
(2)
【解析】粒子竖直方向先做 时间的匀加速运动,然后做 时间的匀速运动,再做 时间的匀加速运动:
,,。
(3)
【解析】竖直方向一共加速运动了 时间,匀速运动了 时间,
则 。
9. (1) ;
【解析】电子经过电容器内的电场后,速度要发生变化,设在 时间内,穿出 板后速度为 ,
时间内射出 板电子的速度 ,
据动能定理有:,,
将 代入上式,得 ,。
(2)
【解析】在 时间内射出板电子在偏转电场中,电子的运动时间:,侧移量: 得:
,
打在荧光屏上的坐标为 ,则:
,
同理可得在 时间内设穿出 板后电子侧移量:
,
打在荧光屏上的坐标:,
故两个发光点之间的距离:
。
(3)
【解析】要求在某一时刻形成均匀分布的一段电子束,前后两段电子束的长度必须相等(且刚好重叠),
第一束长度:,
第二束长度:,,
解得:。
第1页(共1 页)
同课章节目录
- 第九章 静电场及其应用
- 1 电荷
- 2 库仑定律
- 3 电场 电场强度
- 4 静电的防止与利用
- 第十章 静电场中的能量
- 1 电势能和电势
- 2 电势差
- 3 电势差与电场强度的关系
- 4 电容器的电容
- 5 带电粒子在电场中的运动
- 第十一章 电路及其应用
- 1 电源和电流
- 2 导体的电阻
- 3 实验:导体电阻率的测量
- 4 串联电路和并联电路
- 5 实验:练习使用多用电表
- 第十二章 电能 能量守恒定律
- 1 电路中的能量转化
- 2 闭合电路的欧姆定律
- 3 实验:电池电动势和内阻的测量
- 4 能源与可持续发展
- 第十三章 电磁感应与电磁波初步
- 1 磁场 磁感线
- 2 磁感应强度 磁通量
- 3 电磁感应现象及应用
- 4 电磁波的发现及应用
- 5 能量量子化
