19.1.2 函数的图像 教案-2020-2021学年八年级数学人教版下册
文档属性
| 名称 | 19.1.2 函数的图像 教案-2020-2021学年八年级数学人教版下册 |
|
|
| 格式 | doc | ||
| 文件大小 | 809.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-17 00:00:00 | ||
图片预览

文档简介
19.1.2函数的图像
教学目标
(一)知识与技能:进一步理解掌握确定函数关系式.会确定自变量取值范围.
(二)过程与方法:会用变化的量描述事物
(三)情感与价值观要求:会用运动的观点观察事物,分析事物
教学重点:
1.进一步掌握确定函数关系的方法.
2.确定自变量的取值范围.
教学难点:认识函数、领会函数的意义.
教学方法:引导法、合作学习
教学过程
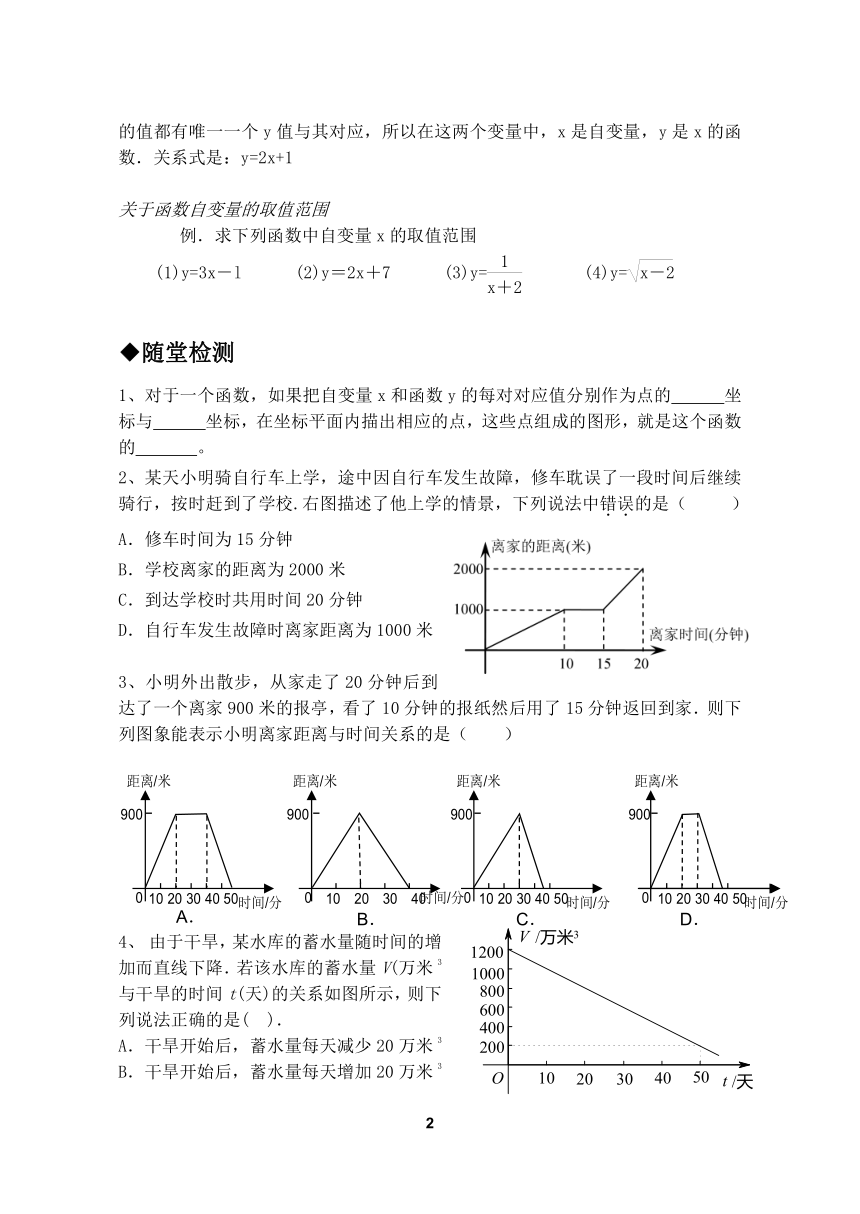
在计算器上按照下面的程序进行操作:
填表:
x 1 3 -4 0 101
y
显示的数y是输入的数x的函数吗?为什么?
2.在计算器上按照下面的程序进行操作.
下表中的x与y是输入的5个数与相应的计算结果:
x 1 2 3 0 -1
y 3 5 7 2 -1
所按的第三、四两个键是哪两个键?y是x的函数吗?如果存在,写出它的表达式(用含有x的式子表示y).
活动结论:
1.从计算结果完全可以看出,每输入一个x的值,操作后都有一个唯一的y值与其对应,所以在这两个变量中,x是自变量、y是x的函数.
2.从表中两行数据中不难看出第三、四按键是这两个键,且每个x的值都有唯一一个y值与其对应,所以在这两个变量中,x是自变量,y是x的函数.关系式是:y=2x+1
关于函数自变量的取值范围
例.求下列函数中自变量x的取值范围
(1)y=3x-l (2)y=2x+7 (3)y= (4)y=
◆随堂检测
1、对于一个函数,如果把自变量x和函数y的每对对应值分别作为点的 坐标与 坐标,在坐标平面内描出相应的点,这些点组成的图形,就是这个函数的 。
2、某天小明骑自行车上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校.右图描述了他上学的情景,下列说法中错误的是( )
A.修车时间为15分钟
B.学校离家的距离为2000米
C.到达学校时共用时间20分钟
D.自行车发生故障时离家距离为1000米
3、小明外出散步,从家走了20分钟后到达了一个离家900米的报亭,看了10分钟的报纸然后用了15分钟返回到家.则下列图象能表示小明离家距离与时间关系的是( )
4、 由于干旱,某水库的蓄水量随时间的增加而直线下降.若该水库的蓄水量V(万米3)与干旱的时间t(天)的关系如图所示,则下列说法正确的是( ).
A.干旱开始后,蓄水量每天减少20万米3
B.干旱开始后,蓄水量每天增加20万米3
C.干旱开始时,蓄水量为200万米3
D.干旱第50天时,蓄水量为1 200万米3
5、(贵州黔东南州)如图,在凯里一中学生耐力测试比赛中,甲、乙两学生测试的路程s(米)与时间t(秒)之间的函数关系的图象分别为折线OABC和线段OD,下列说法正确的是( )
A.乙比甲先到终点
B.乙测试的速度随时间增加而增大
C.比赛过程中(除去起点终点)两人相遇两次
D.比赛全程甲的测试速度始终比乙的测试速度快
◆典例分析
例题:下列四个图象中,不表示某一函数图象的是( ).
分析:A、B、C都是一个自变量的值对应唯一的因变量的值。D图一个自变量的值对应两个因变量的值,不符合函数定义。所以D图不能用函数式表示出来。
解:选D
●拓展提高
1、如图,一个蓄水桶,60分钟可将一满桶水放干.其中,水位h(cm)随着放水时间t(分)的变化而变化.放水速度恒定,h与t的函数的大致图像为( ).
2、如图是小明从学校到家里行进的路程(米)与时间(分)的函数图象.观察图象,从中得到如下信息:学校离小明家1000米;小明用了20分钟到家;小明前10分钟走了路程的一半;④小明后10分钟比前10分钟走的快,其中正确的有___________(填序号).
3、如图,平面直角坐标系中,在边长为1的正方形的边上有一动点沿运动一周,则的纵坐标与点走过的路程之间的函数关系用图象表示大致是( )
4、星期天,小明从家里出发到图书馆去看书,再回到家.他离家的距离y(千米)与时间t(分钟)的关系如图7所示.根据图象回答下列问题:
(1)小明家离图书馆的距离是____________千米;
(2)小明在图书馆看书的时间为___________小时;
(3)小明去图书馆时的速度是______________千米/小时.
5、某校部分住校生,放学后到学校锅炉房打水,每人接水2升,他们先同时打开两个放水笼头,后来因故障关闭一个放水笼头.假设前后两人接水间隔时间忽略不计,且不发生泼洒,锅炉内的余水量y(升)与接水时间x(分)的函数图象如图.
请结合图象,回答下列问题:
(1)根据图中信息,请你写出一个结论;
(2)问前15位同学接水结束共需要几分钟
(3)小敏说:“今天我们寝室的8位同学去锅炉房连续接完水恰好用了3分钟.”你说可能吗 请说明理由.
10 20 30 40 50
900
0
A.
时间/分
距离/米
900
距离/米
900
距离/米
900
距离/米
10 20 30 40
0
时间/分
10 20 30 40 50
0
时间/分
10 20 30 40 50
0
时间/分
B.
C.
D.
10
20
0
1000
s(米)
t(分)
2
教学目标
(一)知识与技能:进一步理解掌握确定函数关系式.会确定自变量取值范围.
(二)过程与方法:会用变化的量描述事物
(三)情感与价值观要求:会用运动的观点观察事物,分析事物
教学重点:
1.进一步掌握确定函数关系的方法.
2.确定自变量的取值范围.
教学难点:认识函数、领会函数的意义.
教学方法:引导法、合作学习
教学过程
在计算器上按照下面的程序进行操作:
填表:
x 1 3 -4 0 101
y
显示的数y是输入的数x的函数吗?为什么?
2.在计算器上按照下面的程序进行操作.
下表中的x与y是输入的5个数与相应的计算结果:
x 1 2 3 0 -1
y 3 5 7 2 -1
所按的第三、四两个键是哪两个键?y是x的函数吗?如果存在,写出它的表达式(用含有x的式子表示y).
活动结论:
1.从计算结果完全可以看出,每输入一个x的值,操作后都有一个唯一的y值与其对应,所以在这两个变量中,x是自变量、y是x的函数.
2.从表中两行数据中不难看出第三、四按键是这两个键,且每个x的值都有唯一一个y值与其对应,所以在这两个变量中,x是自变量,y是x的函数.关系式是:y=2x+1
关于函数自变量的取值范围
例.求下列函数中自变量x的取值范围
(1)y=3x-l (2)y=2x+7 (3)y= (4)y=
◆随堂检测
1、对于一个函数,如果把自变量x和函数y的每对对应值分别作为点的 坐标与 坐标,在坐标平面内描出相应的点,这些点组成的图形,就是这个函数的 。
2、某天小明骑自行车上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校.右图描述了他上学的情景,下列说法中错误的是( )
A.修车时间为15分钟
B.学校离家的距离为2000米
C.到达学校时共用时间20分钟
D.自行车发生故障时离家距离为1000米
3、小明外出散步,从家走了20分钟后到达了一个离家900米的报亭,看了10分钟的报纸然后用了15分钟返回到家.则下列图象能表示小明离家距离与时间关系的是( )
4、 由于干旱,某水库的蓄水量随时间的增加而直线下降.若该水库的蓄水量V(万米3)与干旱的时间t(天)的关系如图所示,则下列说法正确的是( ).
A.干旱开始后,蓄水量每天减少20万米3
B.干旱开始后,蓄水量每天增加20万米3
C.干旱开始时,蓄水量为200万米3
D.干旱第50天时,蓄水量为1 200万米3
5、(贵州黔东南州)如图,在凯里一中学生耐力测试比赛中,甲、乙两学生测试的路程s(米)与时间t(秒)之间的函数关系的图象分别为折线OABC和线段OD,下列说法正确的是( )
A.乙比甲先到终点
B.乙测试的速度随时间增加而增大
C.比赛过程中(除去起点终点)两人相遇两次
D.比赛全程甲的测试速度始终比乙的测试速度快
◆典例分析
例题:下列四个图象中,不表示某一函数图象的是( ).
分析:A、B、C都是一个自变量的值对应唯一的因变量的值。D图一个自变量的值对应两个因变量的值,不符合函数定义。所以D图不能用函数式表示出来。
解:选D
●拓展提高
1、如图,一个蓄水桶,60分钟可将一满桶水放干.其中,水位h(cm)随着放水时间t(分)的变化而变化.放水速度恒定,h与t的函数的大致图像为( ).
2、如图是小明从学校到家里行进的路程(米)与时间(分)的函数图象.观察图象,从中得到如下信息:学校离小明家1000米;小明用了20分钟到家;小明前10分钟走了路程的一半;④小明后10分钟比前10分钟走的快,其中正确的有___________(填序号).
3、如图,平面直角坐标系中,在边长为1的正方形的边上有一动点沿运动一周,则的纵坐标与点走过的路程之间的函数关系用图象表示大致是( )
4、星期天,小明从家里出发到图书馆去看书,再回到家.他离家的距离y(千米)与时间t(分钟)的关系如图7所示.根据图象回答下列问题:
(1)小明家离图书馆的距离是____________千米;
(2)小明在图书馆看书的时间为___________小时;
(3)小明去图书馆时的速度是______________千米/小时.
5、某校部分住校生,放学后到学校锅炉房打水,每人接水2升,他们先同时打开两个放水笼头,后来因故障关闭一个放水笼头.假设前后两人接水间隔时间忽略不计,且不发生泼洒,锅炉内的余水量y(升)与接水时间x(分)的函数图象如图.
请结合图象,回答下列问题:
(1)根据图中信息,请你写出一个结论;
(2)问前15位同学接水结束共需要几分钟
(3)小敏说:“今天我们寝室的8位同学去锅炉房连续接完水恰好用了3分钟.”你说可能吗 请说明理由.
10 20 30 40 50
900
0
A.
时间/分
距离/米
900
距离/米
900
距离/米
900
距离/米
10 20 30 40
0
时间/分
10 20 30 40 50
0
时间/分
10 20 30 40 50
0
时间/分
B.
C.
D.
10
20
0
1000
s(米)
t(分)
2
