备考2022中考数学一轮复习教案 反比例函数(含答案)
文档属性
| 名称 | 备考2022中考数学一轮复习教案 反比例函数(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 229.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-17 16:29:39 | ||
图片预览

文档简介
第三单元 函数及其图像
第13课时 反比例函数
教学目标
【考试目标】
1.了解反比例函数的意义,根据已知条件确定反比例函数的表达式;会用待定系数法求函数的表达式.
2.会画反比例函数的图象,根据反比例函数的图象性质和解析表达式理解其性质.
【教学重点】
了解反比例函数的概念,以及反比例函数解析式的变形.
掌握反比例函数的图象与性质.
掌握用待定系数法求反比例函数的解析式.
熟悉反比例函数与其他几何图形结合.
教学过程
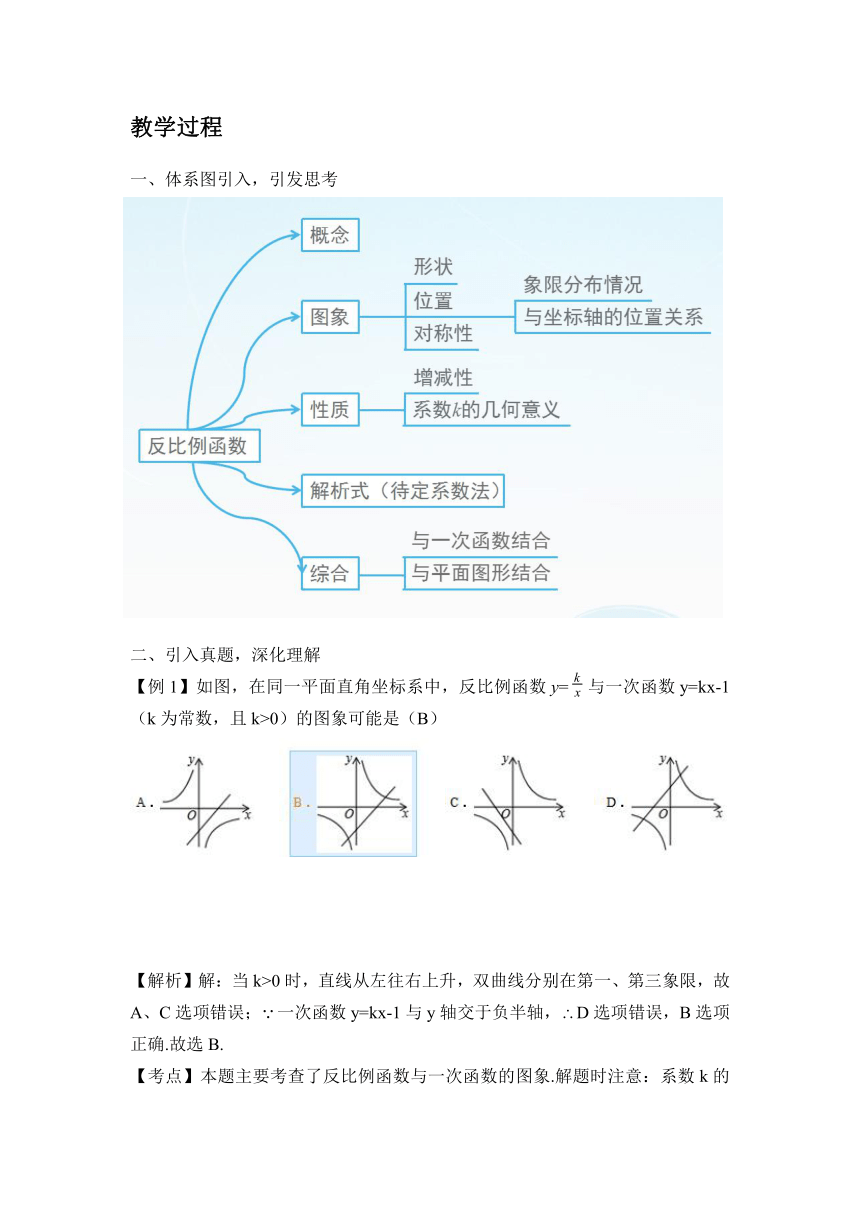
体系图引入,引发思考
引入真题,深化理解
【例1】如图,在同一平面直角坐标系中,反比例函数y=与一次函数y=kx-1(k为常数,且k>0)的图象可能是(B)
【解析】解:当k>0时,直线从左往右上升,双曲线分别在第一、第三象限,故A、C选项错误;一次函数y=kx-1与y轴交于负半轴,D选项错误,B选项正确.故选B.
【考点】本题主要考查了反比例函数与一次函数的图象.解题时注意:系数k的符号决定直线的方向以及双曲线的位置.
【例2】已知反比例函数 ,当1<x<3时,y的最小整数值是 (A)
A.3 B.4 C.5 D.6
【解析】∵6>0,∴该反比例函数在1<x<3单调递减,此时y的范围为2<y<6.∴y的最小整数值是3.故选择A.
【考点】考查了反比例函数的增减性.掌握了反比例函数的增减性,此题不难解出.
【例3】根据图1的程序,得到了y与x轴的函数图象,如图2,若点M是y轴正半轴上任意一点,过点M作PQ∥x轴交图象于点P,Q,连接OP,OQ,则下列结论:①x<0时,y=;②△OPQ的面积为定值;③x>0,y随x的增大而增大;④MQ=2PM;⑤∠POQ可以等于90°.其中正确的有(B)
A.2个 B.3个 C.4个 D.5个
【解析】解:①、x<0时,y=-.故此选项①错误;②、当x<0时,y=-.当x>0时,y=.设P(a,b),Q(c,d).则ab=-2,cd=4.△OPQ的面积是(-a)b+cd=3.故此选项②正确;③、x>0时,y==4·,y随x的增大而减小,故此选项③错误;④、ab=-2,cd=4.故此选项④正确;⑤设PM=-a,则OM=-,则PO =PM +OM =(-a) +(-) =(-a) +.QO =MQ +OM =(-2a) +(-) =4a +.当PQ =PO +QO =(-a) ++4a +=5a +=9a ,整理得:=4a .=2.a有解,∠POQ=90°可能存在.故此选项⑤正确;正确的有②④⑤,故答案为:②④⑤.
【考点】本题主要考查对反比例函数的性质,反比例函数图象上点的坐标特征,三角形的面积等知识点的理解和掌握.
【例4】如图,一次函数y=kx+b的图象分别与反比例函数 的图象在第一象限内交于点A(4,3),与y轴负半轴交于点B,且OA=OB.
(1)求函数y=kx+b和 的表达式;
(2)已知点C(0,5),试在该一次函数图象上确定一点M,使得MB=MC,求此时点M的坐标.
【解析】(1)把点A(4,3)代入函数 得:a=12,
∴ .
∵OA=OB,∴OB=5,∴点B的坐标为(0,-5).
把B(0,-5),A(4,3)代入y=kx+b得: 解得 .
∴y=2x-5.
(2)∵点M在一次函数y=2x-5上,设点M坐标为(x,2x-5),
∵MB=MC,∴
解得:x=2.5,∴点M的坐标为(2.5,0).
【考点】本题考查了反比例函数与一次函数的综合应用,考查了利用待定系数法求反比例函数以及一次函数的解析式,考查了点到点的距离等.
【例5】在平面直角坐标系中,一次函数y=ax+b(a≠0)的图形与反比例函数 (k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3, 点B的坐标为(m,-2).
(1)求△AOH的周长;
(2)求反比例函数和一次函数的解析式.
【解析】(1)由OH=3, ,得AH=4.
即A(-4,3).
根据勾股定理得:
△AOH的周长=AO+AH+OH=3+4+5=12.
(2)将A点坐标代入 (k≠0),得k=-4×3=-12,
反比例函数的解析式为 ;
当y=-2时, ,解得x=6,即B(6,-2).
将A、B点坐标代入y=ax+b,得
解得
一次函数的解析式为
【考点】此题考查了一次函数与反比例函数的交点问题,利用待定系数法是解决此题的关键.
三、师生互动,总结知识
先小组内交流收获和感想,而后以小组为单位派代表进行总结.教师作以补充.
课后作业
布置作业:同步导练
教学反思
同学们对本节内容理解很好,但是对于那些反比例函数与其他知识结合的综合性问题略有欠缺,希望大家下课后能多加练习,巩固知识,提升自己.
第13课时 反比例函数
教学目标
【考试目标】
1.了解反比例函数的意义,根据已知条件确定反比例函数的表达式;会用待定系数法求函数的表达式.
2.会画反比例函数的图象,根据反比例函数的图象性质和解析表达式理解其性质.
【教学重点】
了解反比例函数的概念,以及反比例函数解析式的变形.
掌握反比例函数的图象与性质.
掌握用待定系数法求反比例函数的解析式.
熟悉反比例函数与其他几何图形结合.
教学过程
体系图引入,引发思考
引入真题,深化理解
【例1】如图,在同一平面直角坐标系中,反比例函数y=与一次函数y=kx-1(k为常数,且k>0)的图象可能是(B)
【解析】解:当k>0时,直线从左往右上升,双曲线分别在第一、第三象限,故A、C选项错误;一次函数y=kx-1与y轴交于负半轴,D选项错误,B选项正确.故选B.
【考点】本题主要考查了反比例函数与一次函数的图象.解题时注意:系数k的符号决定直线的方向以及双曲线的位置.
【例2】已知反比例函数 ,当1<x<3时,y的最小整数值是 (A)
A.3 B.4 C.5 D.6
【解析】∵6>0,∴该反比例函数在1<x<3单调递减,此时y的范围为2<y<6.∴y的最小整数值是3.故选择A.
【考点】考查了反比例函数的增减性.掌握了反比例函数的增减性,此题不难解出.
【例3】根据图1的程序,得到了y与x轴的函数图象,如图2,若点M是y轴正半轴上任意一点,过点M作PQ∥x轴交图象于点P,Q,连接OP,OQ,则下列结论:①x<0时,y=;②△OPQ的面积为定值;③x>0,y随x的增大而增大;④MQ=2PM;⑤∠POQ可以等于90°.其中正确的有(B)
A.2个 B.3个 C.4个 D.5个
【解析】解:①、x<0时,y=-.故此选项①错误;②、当x<0时,y=-.当x>0时,y=.设P(a,b),Q(c,d).则ab=-2,cd=4.△OPQ的面积是(-a)b+cd=3.故此选项②正确;③、x>0时,y==4·,y随x的增大而减小,故此选项③错误;④、ab=-2,cd=4.故此选项④正确;⑤设PM=-a,则OM=-,则PO =PM +OM =(-a) +(-) =(-a) +.QO =MQ +OM =(-2a) +(-) =4a +.当PQ =PO +QO =(-a) ++4a +=5a +=9a ,整理得:=4a .=2.a有解,∠POQ=90°可能存在.故此选项⑤正确;正确的有②④⑤,故答案为:②④⑤.
【考点】本题主要考查对反比例函数的性质,反比例函数图象上点的坐标特征,三角形的面积等知识点的理解和掌握.
【例4】如图,一次函数y=kx+b的图象分别与反比例函数 的图象在第一象限内交于点A(4,3),与y轴负半轴交于点B,且OA=OB.
(1)求函数y=kx+b和 的表达式;
(2)已知点C(0,5),试在该一次函数图象上确定一点M,使得MB=MC,求此时点M的坐标.
【解析】(1)把点A(4,3)代入函数 得:a=12,
∴ .
∵OA=OB,∴OB=5,∴点B的坐标为(0,-5).
把B(0,-5),A(4,3)代入y=kx+b得: 解得 .
∴y=2x-5.
(2)∵点M在一次函数y=2x-5上,设点M坐标为(x,2x-5),
∵MB=MC,∴
解得:x=2.5,∴点M的坐标为(2.5,0).
【考点】本题考查了反比例函数与一次函数的综合应用,考查了利用待定系数法求反比例函数以及一次函数的解析式,考查了点到点的距离等.
【例5】在平面直角坐标系中,一次函数y=ax+b(a≠0)的图形与反比例函数 (k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3, 点B的坐标为(m,-2).
(1)求△AOH的周长;
(2)求反比例函数和一次函数的解析式.
【解析】(1)由OH=3, ,得AH=4.
即A(-4,3).
根据勾股定理得:
△AOH的周长=AO+AH+OH=3+4+5=12.
(2)将A点坐标代入 (k≠0),得k=-4×3=-12,
反比例函数的解析式为 ;
当y=-2时, ,解得x=6,即B(6,-2).
将A、B点坐标代入y=ax+b,得
解得
一次函数的解析式为
【考点】此题考查了一次函数与反比例函数的交点问题,利用待定系数法是解决此题的关键.
三、师生互动,总结知识
先小组内交流收获和感想,而后以小组为单位派代表进行总结.教师作以补充.
课后作业
布置作业:同步导练
教学反思
同学们对本节内容理解很好,但是对于那些反比例函数与其他知识结合的综合性问题略有欠缺,希望大家下课后能多加练习,巩固知识,提升自己.
同课章节目录
