备考2022中考数学一轮复习教案 函数的应用(含答案)
文档属性
| 名称 | 备考2022中考数学一轮复习教案 函数的应用(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 165.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-17 16:33:10 | ||
图片预览

文档简介
第三单元 函数及其图像
第15课时 函数的应用
教学目标
【考试目标】
用一次函数、反比例函数、二次函数解决简单的实际问题.
【教学重点】
学会利用函数知识解应用题的一般步骤.
会构建函数模型.
会在实际问题中求函数解析式.
教学过程
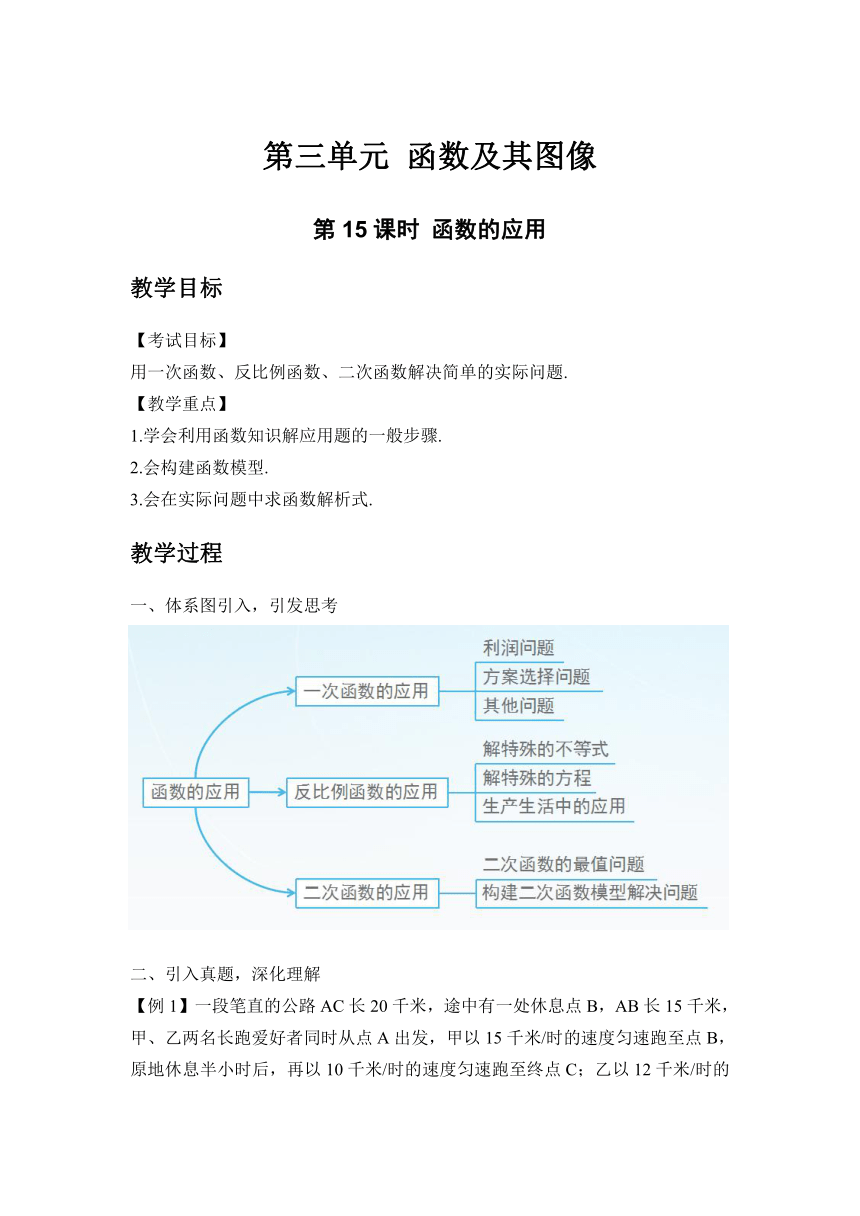
体系图引入,引发思考
引入真题,深化理解
【例1】一段笔直的公路AC长20千米,途中有一处休息点B,AB长15千米,甲、乙两名长跑爱好者同时从点A出发,甲以15千米/时的速度匀速跑至点B,原地休息半小时后,再以10千米/时的速度匀速跑至终点C;乙以12千米/时的速度匀速跑至终点C,下列选项中,能正确反映甲、乙两人出发后2小时内运动路程 y(千米)与时间 x(小时)函数关系的图象是 (A)
【解析】根据题意可知甲两小时内运动路程与时间的关系为分段函数,共分为3段,第一段,0≤x≤1时,图象为一条过原点的倾斜线段,且斜率较大,并且过点(1,15).第二段,当1<x< 时,图象为平行于x轴的一条线段.第三段,当
≤x≤2时,图象为一条倾斜的线段,且斜率小于第一段图象的斜率,故可排除B、D;因为 (小时)乙两小时内运动路程与时间的关系也分段,分为两段,第一段图象为倾斜线段,过原点与点 ,且斜率小于甲的第一段,大于甲的第三段.第二段图象也为平行于x轴的线段,故可以排除C,所以选择A选项.
【例2】足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如下表:
下列结论:①足球距离地面的最大高度为20m;②足球飞行路线的对称轴是直线t=;③足球被踢出9s时落地;④足球被踢出1.5秒时,距离地面的高度是11m.其中正确结论的个数是 (B)
A.1 B.2 C.3 D.4
【解析】解:由题意,抛物线的解析式为y=at(t-9),把(1,8)代入可得a=-1.
y=-t +9t=-(t-4.5) +20.25.
足球距离地面的最大高度为20.25m,故①错误.
抛物线的对称轴t=4.5,故②正确.
t=9时,y=0,
足球被踢出9s时落地,故③正确.
t=1.5时,y=11.25,故 ④错误.
正确的有②③.故选B.
【例3】已知二次函数y=x +2x+m +2m-1(m为常数),当自变量x的值满足1x3时,与其对应的函数值y的最小值为5,则m的值为 (C)
A.1或-5 B.-1或5 C.1或-3 D.1或3
【解析】解:y=x +2x+m +2m-1=(x+1) +m +2m-2,当x>-1时,y随x的增大而增大.根据题意,当x=1时,有m +2m+2=5.解得:m=1或m=-3.故选C.
三、师生互动,总结知识
先小组内交流收获和感想,而后以小组为单位派代表进行总结.教师作以补充.
课后作业
布置作业:同步导练
教学反思
本课时内容单独理解并不是很难,但是要熟练应用,还要结合其他知识熟练掌握很难,大家要多多练习,尽可能熟练的掌握本课时的知识.
第15课时 函数的应用
教学目标
【考试目标】
用一次函数、反比例函数、二次函数解决简单的实际问题.
【教学重点】
学会利用函数知识解应用题的一般步骤.
会构建函数模型.
会在实际问题中求函数解析式.
教学过程
体系图引入,引发思考
引入真题,深化理解
【例1】一段笔直的公路AC长20千米,途中有一处休息点B,AB长15千米,甲、乙两名长跑爱好者同时从点A出发,甲以15千米/时的速度匀速跑至点B,原地休息半小时后,再以10千米/时的速度匀速跑至终点C;乙以12千米/时的速度匀速跑至终点C,下列选项中,能正确反映甲、乙两人出发后2小时内运动路程 y(千米)与时间 x(小时)函数关系的图象是 (A)
【解析】根据题意可知甲两小时内运动路程与时间的关系为分段函数,共分为3段,第一段,0≤x≤1时,图象为一条过原点的倾斜线段,且斜率较大,并且过点(1,15).第二段,当1<x< 时,图象为平行于x轴的一条线段.第三段,当
≤x≤2时,图象为一条倾斜的线段,且斜率小于第一段图象的斜率,故可排除B、D;因为 (小时)乙两小时内运动路程与时间的关系也分段,分为两段,第一段图象为倾斜线段,过原点与点 ,且斜率小于甲的第一段,大于甲的第三段.第二段图象也为平行于x轴的线段,故可以排除C,所以选择A选项.
【例2】足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如下表:
下列结论:①足球距离地面的最大高度为20m;②足球飞行路线的对称轴是直线t=;③足球被踢出9s时落地;④足球被踢出1.5秒时,距离地面的高度是11m.其中正确结论的个数是 (B)
A.1 B.2 C.3 D.4
【解析】解:由题意,抛物线的解析式为y=at(t-9),把(1,8)代入可得a=-1.
y=-t +9t=-(t-4.5) +20.25.
足球距离地面的最大高度为20.25m,故①错误.
抛物线的对称轴t=4.5,故②正确.
t=9时,y=0,
足球被踢出9s时落地,故③正确.
t=1.5时,y=11.25,故 ④错误.
正确的有②③.故选B.
【例3】已知二次函数y=x +2x+m +2m-1(m为常数),当自变量x的值满足1x3时,与其对应的函数值y的最小值为5,则m的值为 (C)
A.1或-5 B.-1或5 C.1或-3 D.1或3
【解析】解:y=x +2x+m +2m-1=(x+1) +m +2m-2,当x>-1时,y随x的增大而增大.根据题意,当x=1时,有m +2m+2=5.解得:m=1或m=-3.故选C.
三、师生互动,总结知识
先小组内交流收获和感想,而后以小组为单位派代表进行总结.教师作以补充.
课后作业
布置作业:同步导练
教学反思
本课时内容单独理解并不是很难,但是要熟练应用,还要结合其他知识熟练掌握很难,大家要多多练习,尽可能熟练的掌握本课时的知识.
同课章节目录
