2021-2022学年北师大版九年级数学下册第三章圆单元综合达标测试(Word版,附答案解析)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册第三章圆单元综合达标测试(Word版,附答案解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-17 00:00:00 | ||
图片预览


文档简介
2021-2022学年北师大版九年级数学下册《第3章圆》单元综合达标测试(附答案)
一、单选题(满分40分)
1.设P为⊙O外一点,若点P到⊙O的最短距离为3,最长距离为7,则⊙O的半径为( )
A.2 B.4 C.4或10 D.2或5
2.如图,在⊙O中,半径OC垂直弦AB于D,点E在⊙O上,∠E=22.5 ,AB=4,则半径OB等于( )
A.1 B.2 C.2 D.
3.如图,点是⊙O外一点,为⊙O的一条割线,且,交⊙O于点,若,,则长为( )
A. B. C. D.
4.如图,在半径为5的⊙中,,是互相垂直的两条弦,垂足为,,则的长为( )
A.3 B.4 C. D.
5.如图所示,直径为10的⊙A经过点C(0,5)和点O(0,0),B是y轴右侧⊙A优弧上一点,则∠OBC的余弦值为( )
A. B. C. D.
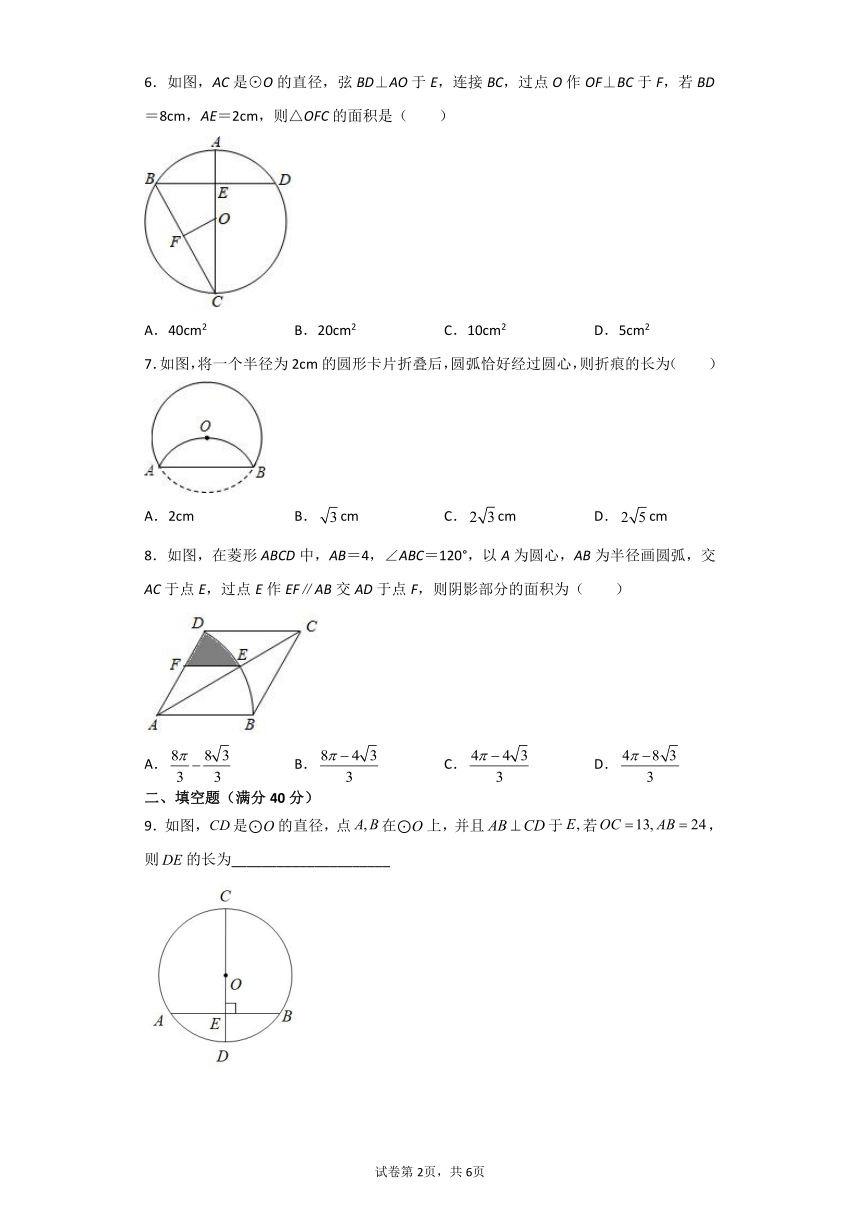
6.如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,则△OFC的面积是( )
A.40cm2 B.20cm2 C.10cm2 D.5cm2
7.如图,将一个半径为2cm的圆形卡片折叠后,圆弧恰好经过圆心,则折痕的长为( )
A.2cm B.cm C.cm D.cm
8.如图,在菱形ABCD中,AB=4,∠ABC=120°,以A为圆心,AB为半径画圆弧,交AC于点E,过点E作EF∥AB交AD于点F,则阴影部分的面积为( )
A. B. C. D.
二、填空题(满分40分)
9.如图,是⊙O的直径,点在⊙O上,并且于若,则的长为_____________________
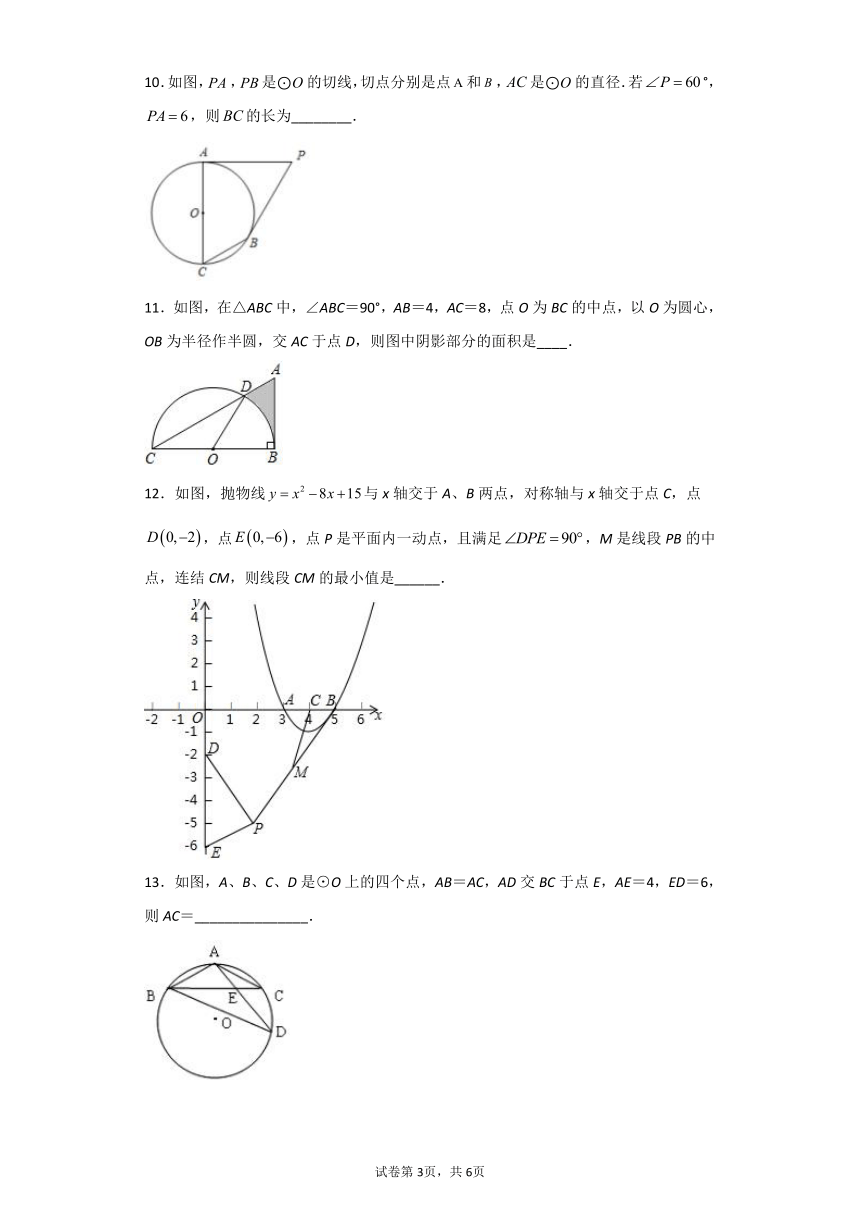
10.如图,,是⊙O的切线,切点分别是点和,是⊙O的直径.若°,,则的长为________.
11.如图,在△ABC中,∠ABC=90°,AB=4,AC=8,点O为BC的中点,以O为圆心,OB为半径作半圆,交AC于点D,则图中阴影部分的面积是____.
12.如图,抛物线与x轴交于A、B两点,对称轴与x轴交于点C,点,点,点P是平面内一动点,且满足,M是线段PB的中点,连结CM,则线段CM的最小值是______.
13.如图,A、B、C、D是⊙O上的四个点,AB=AC,AD交BC于点E,AE=4,ED=6,则AC=_______________.
14.⊙O内一点P,OP=3cm,过点P的最短的弦AB=6cm,Q是⊙O上除AB两点之外的任一点,则∠AQB=____.
15.如图,已知圆O为的内切圆,切点分别为D、E、F,且,,,则圆O的半径为______.
16.已知一个半圆形工件,未搬动前如图所示,直径平行于地面放置,搬动时为了保护圆弧部分不受损伤,先将半圆作如图所示的无滑动翻转,使它的直径紧贴地面,再将它沿地面平移50m,半圆的直径为6m,则圆心O所经过的路线长是____________m.(结果用π表示)
三、解答题(满分40分)
17.如图,AB是⊙O的一条弦,且AB=.点C,E分别在⊙O上,且OC⊥AB于点D,∠E=30°,连接OA.
(1)求OA的长;
(2)若AF是⊙O的另一条弦,且点O到AF的距离为,直接写出∠BAF的度数.
18.如图,AB是⊙O的直径,CD⊥AB于E,连接OC,BC.
(1)若BE=4,CD=16,求OC;
(2)求证:∠ACO=∠BCD.
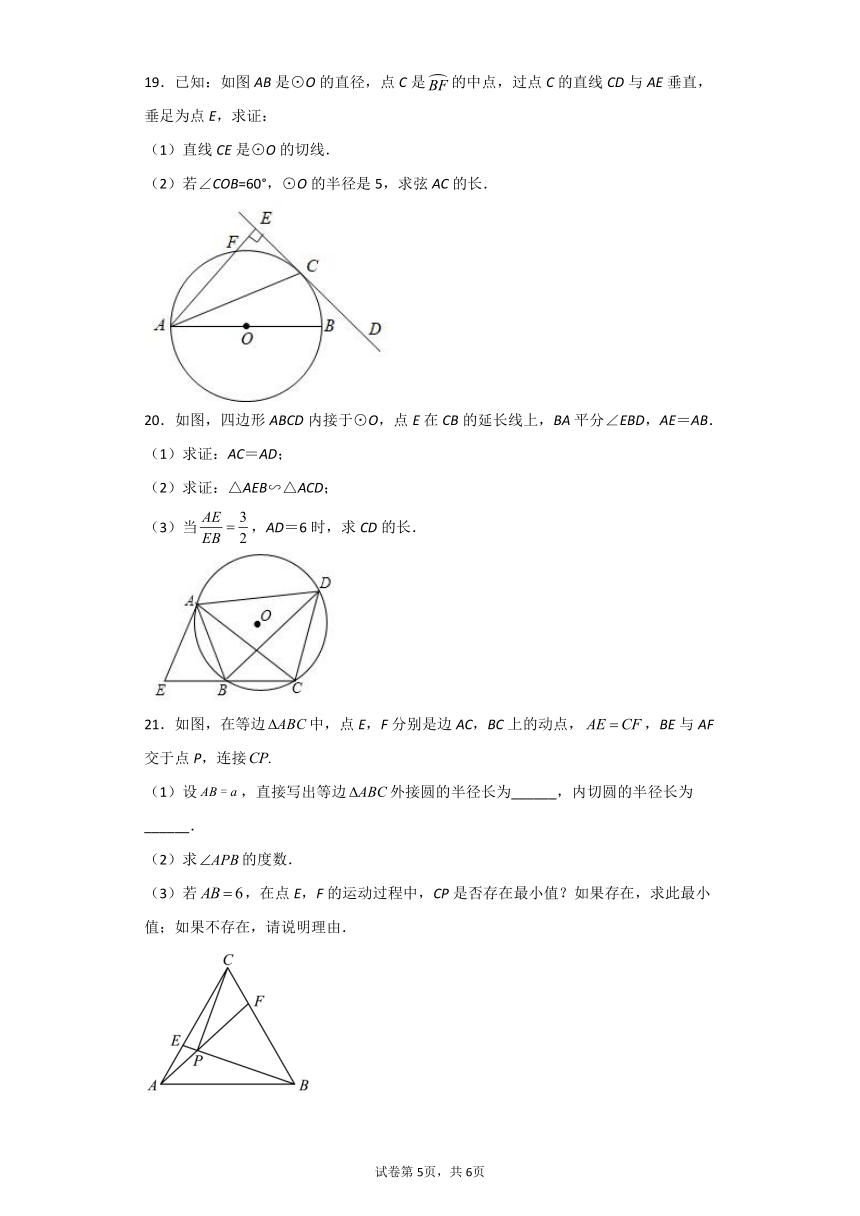
19.已知:如图AB是⊙O的直径,点C是的中点,过点C的直线CD与AE垂直,垂足为点E,求证:
(1)直线CE是⊙O的切线.
(2)若∠COB=60°,⊙O的半径是5,求弦AC的长.
20.如图,四边形ABCD内接于⊙O,点E在CB的延长线上,BA平分∠EBD,AE=AB.
(1)求证:AC=AD;
(2)求证:△AEB∽△ACD;
(3)当,AD=6时,求CD的长.
21.如图,在等边中,点E,F分别是边AC,BC上的动点,,BE与AF交于点P,连接
(1)设,直接写出等边外接圆的半径长为______,内切圆的半径长为______.
(2)求的度数.
(3)若,在点E,F的运动过程中,CP是否存在最小值?如果存在,求此最小值;如果不存在,请说明理由.
22.如图,D为⊙O上一点,点C在直径BA的延长线上,且CD2=CA·CB;
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,若BC=10,,求BE的长.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.A
解:∵P为⊙O外一点,若点P到⊙O的最短距离为3,最长距离为7,
∴⊙O的直径为:7-3=4,
∴⊙O的半径为2,
故选:A.
2.B
解:∵连接AO,半径OC垂直弦AB于D,
∴
∴∠AOC=∠BOC,AD=BD=
∵∠E=22.5 ,
∴∠AOC=22.5°×2=45°=∠BOC
又∵OC⊥AB,AD=BD=2
∴OD=BD=2
∴
故选B.
3.B
解:设PA=AB=x,延长PO交圆于点D.连接BD,AC
∵四边形ABDC内接于
∴
又
∴
∴
∴PA PB=PC PD,
∵OC=3,OP=5,
∴PC=2,PD=5+3=8
∴x 2x=16,
∴x=
∴.
故选:B.
4.C
解:如图,连接 过作 垂足分别为 而
四边形为矩形,
同理:
四边形为正方形,
故选:C
5.C
解:设⊙A交x轴于另一点D,连接CD,作图如下:
∵
∴CD是直径
∴CD=10
∵
∴OC=5
在中,, OC=5, CD=10
由勾股定理得:
即:
∵
∴
∵
∴∠OBC=∠ODC,
∴在中,
故选:C
6.D
解:连接OB,
∵AC是⊙O的直径,弦BD⊥AO于E,BD=8cm,AE=2cm.
∴,
在Rt△OEB中,OE2+BE2=OB2,即OE2+42=(OE+2)2
解得:OE=3cm,
∴,
∴,
∵OB=OC,OF⊥BC,
∴BF=CF,
∴
∴,
故选D.
7.C
解:如图,连接OA,连接点O关于AB的对称点E,交AB于点D,
由折叠得OD=DE=cm,OD⊥AB,
∴AD=BD=,
在Rt△AOD中,,
∴ cm,
∴,故选:C.
8.C
解:过F作FH⊥AC于H,
∵四边形ABCD是菱形,AB=4,
∴∠DAC=∠BAC,AD∥BC,
∴∠ABC+∠DAB=180°,
∵∠ABC=120°,
∴∠DAB=60°,
∴∠DAC=∠BAC=30°,
∵以A为圆心,AD为半径画弧,交AC于点E,AB=4,
∴AE=4,
∵EF∥AB,
∴∠FEA=∠BAC,
∵∠DAC=∠BAC,
∴∠DAC=∠FEA,
∴AF=EF,
∵FH⊥AE,AE=4,
∴AH=EH=2,
∵∠DAC=30°,∠AHF=90°,
∴AF=2FH,
∴(2FH)2=FH2+22,
解得:FH=,
∴阴影部分的面积S=S扇形DAE-S△FAE
,故选:C.
9.
解:连接,如图,
是的直径,,,
在中,
故答案为:
10.
解:∵,是的切线,切点分别是点和
∴,
∴
又∵
∴为等边三角形
∴,
∴
∵是的直径
∴
设,则
由勾股定理得:,即
解得,即
故答案为:.
11.
解:如图所示,过点D作于E,
在中,,,
∴,,
∴,
∵OC=OD,
∴∠OCD=∠ODC=30°
∴,
∵∠DEO=90°,
∴∠ODE=30°,
∵,
∴,
∴,
∴
故答案为:.
12.
解:解方程x2 8x+15=0得x1=3,x2=5,则A(3,0),
∵抛物线的对称轴与x轴交于点C,
∴C点为AB的中点,
∵∠DPE=90°,
∴点P在以DE为直径的圆上,圆心Q点的坐标为(0, 4),
AQ==5,⊙Q的半径为2,
连接AQ交⊙Q于F,此时AF最小,最小值为5-2=3,
连接AP,
∵M是线段PB的中点,
∴CM为△ABP为中位线,
∴CM=AP,
∴CM的最小值为.
故答案为:.
13.
解:∵AB=AC,
∴∠ABE=∠ACE,
∵∠ACE=∠ADB,
∴∠ABE=∠ADB,
∵∠BAE=∠DAB
∴△ABE∽△ADB,
∴,
即AB2=AD AE,
∵AE=4,ED=6,
∴AD=10,
∴AB=,
故答案为:.
14.或
解:如下图当AB⊥OP,AB为过点P的最短的弦且AB=6cm,
连接OA,OB,
∵AB⊥OP,
∴,∠AOB=2∠AOP,
∴,
∴,
当Q点在处时,,
当Q点在处时,,
故答案为:或.
15.2
如图,连接OA、OB、OC、OD、OE、OF
∵⊙O为的内切圆,切点分别为D、E、F
∴OD⊥AB,OE⊥AC,OF⊥BC,且OD=OE=OF
在Rt△ABC中,由勾股定理得
∴
∵
∴
即
∴OD=2
即⊙O的半径为2
故答案为:2
16.(3π+50)50+3π)
解:如图所示,
圆心先向前走的长度即圆的周长,然后沿着弧旋转圆的周长,最后向右平移50米,
∴圆心总共走过的路程为圆周长的一半,即半圆的弧长加上50,
由已知可得圆的半径为3,
设半圆形的弧长为,
则半圆形的弧长为,
故圆心O所经过的路线长;
故答案是(3π+50).
17.(1)4;(2)75°或15°
解:(1)∵AB是⊙O的一条弦,OC⊥AB,AB=.
∴ ,
∵∠E=30°,
∴∠AOC=2∠AEC=60°,
在 中, ;
(2)如图,当AF位于AB的上方时,过点O作OH⊥AF于点H,则 ,
∵OA=4,
在 中,勾股定理得:
,
∴AH=OH,
∴∠OAF=∠AOH=45°,
∵∠AOC=60°,∠ADO=90°,
∴∠OAD=30°,
∴∠BAF=∠OAF+∠OAD=75°,
当AF位于AB的下方时,即弦 ,
同理 =45°,
∴ ,
综上所述,∠BAF的度数为75°或15°.
18.(1)10;(2)
(1)解:∵AB是⊙O的直径,AB⊥弦CD于E,
∴CE=CD=8,
设OC=OB=x,
∴OE=x-4,
∵∠CEO=90°,
∴OC2=OE2+CE2,
∴x2=(x-4)2+82,
∴x=10,
∴OC=10.
(2)证明:∵AB为⊙O的直径,AB⊥CD,
∴,
∴∠BCD=∠BAC
∵OA=OC,
∴∠BAC=∠ACO,
∴∠ACO=∠BCD.
19.(1)(2)
(1)证明:如图,连接,
点C是的中点,
又
即
直线CE是⊙O的切线.
(2)解:如图,连接
是的直径,
,⊙O的半径是5,∠COB=60°,
在中,
20.(1);(2);(3)4
(1)证明:∵BA平分∠EBD,
∴∠ABE=∠ABD,
∵四边形ABCD内接于⊙O,
∴∠ABE=∠ADC,∠ABD=∠ACD,
∴∠ACD=∠ADC,
∴AC=AD;
(2)证明:∵AE=AB,
∴∠E=∠ABE,
∵∠ABE=∠ADC,
∴∠E=∠ABE=∠ACD=∠ADC,
∴△AEB∽△ACD;
(3)解:由(2)知,△AEB∽△ACD,
∴
∵AC=AD=6,
∴,
∴CD==4.
21.(1);; (2);(3)的最小值
解:(1)如图,点O为等边△ABC外接圆的圆心,也是内切圆的圆心,作OD⊥AB于点D,连接OA,
∵等边三角形的边长AB为a,
∴AD=,
又∵∠DAO=∠BAC=60°×=30°,
∴.
∵DO为内切圆半径,
∴.
故答案为:a,a.
(2)∵△ABC为等边三角形,
∴AB=AC,∠C=∠CAB=60°,
又∵AE=CF,
在△ABE和△CAF中,
,
∴△ABE≌△CAF(SAS);
∴AF=BE,∠ABE=∠CAF.
又∵∠APE=∠BPF=∠ABP+∠BAP,
∴∠APE=∠BAP+∠CAF=60°.
∴∠APB=180°-∠APE=120°.
(3)CP存在最小值.
如图,过点A,点P,点B作⊙O,连接CO,PO,则点P在上运动,
∵AO=OP=OB,
∴∠OAP=∠OPA,∠OPB=∠OBP,∠OAB=∠OBA,
∴∠AOB=360°-∠OAP-∠OPA-∠OPB-∠OBP=120°,
∴∠OAB=30°,
∴∠CAO=90°,
∵AC=BC,OA=OB,
∴CO垂直平分AB,
∴∠ACO=30°,
∴cos∠ACO=,CO=2AO,
∴CO=4,
∴AO=2,
在△CPO中,CP≥CO-OP,
∴当点P在CO上时,CP有最小值,
∴CP的最小值=4-2=2,
22.(1);(2)
(1)
如图,连接,
,
∴CD:CA=CB:CD,
又,
,
,
、为半径
,
为的直径,
,
,
,
为的切线;
(2),是的切线,
,
,
,
,
,
设,则,,
在中,,
解得:,
.
一、单选题(满分40分)
1.设P为⊙O外一点,若点P到⊙O的最短距离为3,最长距离为7,则⊙O的半径为( )
A.2 B.4 C.4或10 D.2或5
2.如图,在⊙O中,半径OC垂直弦AB于D,点E在⊙O上,∠E=22.5 ,AB=4,则半径OB等于( )
A.1 B.2 C.2 D.
3.如图,点是⊙O外一点,为⊙O的一条割线,且,交⊙O于点,若,,则长为( )
A. B. C. D.
4.如图,在半径为5的⊙中,,是互相垂直的两条弦,垂足为,,则的长为( )
A.3 B.4 C. D.
5.如图所示,直径为10的⊙A经过点C(0,5)和点O(0,0),B是y轴右侧⊙A优弧上一点,则∠OBC的余弦值为( )
A. B. C. D.
6.如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,则△OFC的面积是( )
A.40cm2 B.20cm2 C.10cm2 D.5cm2
7.如图,将一个半径为2cm的圆形卡片折叠后,圆弧恰好经过圆心,则折痕的长为( )
A.2cm B.cm C.cm D.cm
8.如图,在菱形ABCD中,AB=4,∠ABC=120°,以A为圆心,AB为半径画圆弧,交AC于点E,过点E作EF∥AB交AD于点F,则阴影部分的面积为( )
A. B. C. D.
二、填空题(满分40分)
9.如图,是⊙O的直径,点在⊙O上,并且于若,则的长为_____________________
10.如图,,是⊙O的切线,切点分别是点和,是⊙O的直径.若°,,则的长为________.
11.如图,在△ABC中,∠ABC=90°,AB=4,AC=8,点O为BC的中点,以O为圆心,OB为半径作半圆,交AC于点D,则图中阴影部分的面积是____.
12.如图,抛物线与x轴交于A、B两点,对称轴与x轴交于点C,点,点,点P是平面内一动点,且满足,M是线段PB的中点,连结CM,则线段CM的最小值是______.
13.如图,A、B、C、D是⊙O上的四个点,AB=AC,AD交BC于点E,AE=4,ED=6,则AC=_______________.
14.⊙O内一点P,OP=3cm,过点P的最短的弦AB=6cm,Q是⊙O上除AB两点之外的任一点,则∠AQB=____.
15.如图,已知圆O为的内切圆,切点分别为D、E、F,且,,,则圆O的半径为______.
16.已知一个半圆形工件,未搬动前如图所示,直径平行于地面放置,搬动时为了保护圆弧部分不受损伤,先将半圆作如图所示的无滑动翻转,使它的直径紧贴地面,再将它沿地面平移50m,半圆的直径为6m,则圆心O所经过的路线长是____________m.(结果用π表示)
三、解答题(满分40分)
17.如图,AB是⊙O的一条弦,且AB=.点C,E分别在⊙O上,且OC⊥AB于点D,∠E=30°,连接OA.
(1)求OA的长;
(2)若AF是⊙O的另一条弦,且点O到AF的距离为,直接写出∠BAF的度数.
18.如图,AB是⊙O的直径,CD⊥AB于E,连接OC,BC.
(1)若BE=4,CD=16,求OC;
(2)求证:∠ACO=∠BCD.
19.已知:如图AB是⊙O的直径,点C是的中点,过点C的直线CD与AE垂直,垂足为点E,求证:
(1)直线CE是⊙O的切线.
(2)若∠COB=60°,⊙O的半径是5,求弦AC的长.
20.如图,四边形ABCD内接于⊙O,点E在CB的延长线上,BA平分∠EBD,AE=AB.
(1)求证:AC=AD;
(2)求证:△AEB∽△ACD;
(3)当,AD=6时,求CD的长.
21.如图,在等边中,点E,F分别是边AC,BC上的动点,,BE与AF交于点P,连接
(1)设,直接写出等边外接圆的半径长为______,内切圆的半径长为______.
(2)求的度数.
(3)若,在点E,F的运动过程中,CP是否存在最小值?如果存在,求此最小值;如果不存在,请说明理由.
22.如图,D为⊙O上一点,点C在直径BA的延长线上,且CD2=CA·CB;
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,若BC=10,,求BE的长.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.A
解:∵P为⊙O外一点,若点P到⊙O的最短距离为3,最长距离为7,
∴⊙O的直径为:7-3=4,
∴⊙O的半径为2,
故选:A.
2.B
解:∵连接AO,半径OC垂直弦AB于D,
∴
∴∠AOC=∠BOC,AD=BD=
∵∠E=22.5 ,
∴∠AOC=22.5°×2=45°=∠BOC
又∵OC⊥AB,AD=BD=2
∴OD=BD=2
∴
故选B.
3.B
解:设PA=AB=x,延长PO交圆于点D.连接BD,AC
∵四边形ABDC内接于
∴
又
∴
∴
∴PA PB=PC PD,
∵OC=3,OP=5,
∴PC=2,PD=5+3=8
∴x 2x=16,
∴x=
∴.
故选:B.
4.C
解:如图,连接 过作 垂足分别为 而
四边形为矩形,
同理:
四边形为正方形,
故选:C
5.C
解:设⊙A交x轴于另一点D,连接CD,作图如下:
∵
∴CD是直径
∴CD=10
∵
∴OC=5
在中,, OC=5, CD=10
由勾股定理得:
即:
∵
∴
∵
∴∠OBC=∠ODC,
∴在中,
故选:C
6.D
解:连接OB,
∵AC是⊙O的直径,弦BD⊥AO于E,BD=8cm,AE=2cm.
∴,
在Rt△OEB中,OE2+BE2=OB2,即OE2+42=(OE+2)2
解得:OE=3cm,
∴,
∴,
∵OB=OC,OF⊥BC,
∴BF=CF,
∴
∴,
故选D.
7.C
解:如图,连接OA,连接点O关于AB的对称点E,交AB于点D,
由折叠得OD=DE=cm,OD⊥AB,
∴AD=BD=,
在Rt△AOD中,,
∴ cm,
∴,故选:C.
8.C
解:过F作FH⊥AC于H,
∵四边形ABCD是菱形,AB=4,
∴∠DAC=∠BAC,AD∥BC,
∴∠ABC+∠DAB=180°,
∵∠ABC=120°,
∴∠DAB=60°,
∴∠DAC=∠BAC=30°,
∵以A为圆心,AD为半径画弧,交AC于点E,AB=4,
∴AE=4,
∵EF∥AB,
∴∠FEA=∠BAC,
∵∠DAC=∠BAC,
∴∠DAC=∠FEA,
∴AF=EF,
∵FH⊥AE,AE=4,
∴AH=EH=2,
∵∠DAC=30°,∠AHF=90°,
∴AF=2FH,
∴(2FH)2=FH2+22,
解得:FH=,
∴阴影部分的面积S=S扇形DAE-S△FAE
,故选:C.
9.
解:连接,如图,
是的直径,,,
在中,
故答案为:
10.
解:∵,是的切线,切点分别是点和
∴,
∴
又∵
∴为等边三角形
∴,
∴
∵是的直径
∴
设,则
由勾股定理得:,即
解得,即
故答案为:.
11.
解:如图所示,过点D作于E,
在中,,,
∴,,
∴,
∵OC=OD,
∴∠OCD=∠ODC=30°
∴,
∵∠DEO=90°,
∴∠ODE=30°,
∵,
∴,
∴,
∴
故答案为:.
12.
解:解方程x2 8x+15=0得x1=3,x2=5,则A(3,0),
∵抛物线的对称轴与x轴交于点C,
∴C点为AB的中点,
∵∠DPE=90°,
∴点P在以DE为直径的圆上,圆心Q点的坐标为(0, 4),
AQ==5,⊙Q的半径为2,
连接AQ交⊙Q于F,此时AF最小,最小值为5-2=3,
连接AP,
∵M是线段PB的中点,
∴CM为△ABP为中位线,
∴CM=AP,
∴CM的最小值为.
故答案为:.
13.
解:∵AB=AC,
∴∠ABE=∠ACE,
∵∠ACE=∠ADB,
∴∠ABE=∠ADB,
∵∠BAE=∠DAB
∴△ABE∽△ADB,
∴,
即AB2=AD AE,
∵AE=4,ED=6,
∴AD=10,
∴AB=,
故答案为:.
14.或
解:如下图当AB⊥OP,AB为过点P的最短的弦且AB=6cm,
连接OA,OB,
∵AB⊥OP,
∴,∠AOB=2∠AOP,
∴,
∴,
当Q点在处时,,
当Q点在处时,,
故答案为:或.
15.2
如图,连接OA、OB、OC、OD、OE、OF
∵⊙O为的内切圆,切点分别为D、E、F
∴OD⊥AB,OE⊥AC,OF⊥BC,且OD=OE=OF
在Rt△ABC中,由勾股定理得
∴
∵
∴
即
∴OD=2
即⊙O的半径为2
故答案为:2
16.(3π+50)50+3π)
解:如图所示,
圆心先向前走的长度即圆的周长,然后沿着弧旋转圆的周长,最后向右平移50米,
∴圆心总共走过的路程为圆周长的一半,即半圆的弧长加上50,
由已知可得圆的半径为3,
设半圆形的弧长为,
则半圆形的弧长为,
故圆心O所经过的路线长;
故答案是(3π+50).
17.(1)4;(2)75°或15°
解:(1)∵AB是⊙O的一条弦,OC⊥AB,AB=.
∴ ,
∵∠E=30°,
∴∠AOC=2∠AEC=60°,
在 中, ;
(2)如图,当AF位于AB的上方时,过点O作OH⊥AF于点H,则 ,
∵OA=4,
在 中,勾股定理得:
,
∴AH=OH,
∴∠OAF=∠AOH=45°,
∵∠AOC=60°,∠ADO=90°,
∴∠OAD=30°,
∴∠BAF=∠OAF+∠OAD=75°,
当AF位于AB的下方时,即弦 ,
同理 =45°,
∴ ,
综上所述,∠BAF的度数为75°或15°.
18.(1)10;(2)
(1)解:∵AB是⊙O的直径,AB⊥弦CD于E,
∴CE=CD=8,
设OC=OB=x,
∴OE=x-4,
∵∠CEO=90°,
∴OC2=OE2+CE2,
∴x2=(x-4)2+82,
∴x=10,
∴OC=10.
(2)证明:∵AB为⊙O的直径,AB⊥CD,
∴,
∴∠BCD=∠BAC
∵OA=OC,
∴∠BAC=∠ACO,
∴∠ACO=∠BCD.
19.(1)(2)
(1)证明:如图,连接,
点C是的中点,
又
即
直线CE是⊙O的切线.
(2)解:如图,连接
是的直径,
,⊙O的半径是5,∠COB=60°,
在中,
20.(1);(2);(3)4
(1)证明:∵BA平分∠EBD,
∴∠ABE=∠ABD,
∵四边形ABCD内接于⊙O,
∴∠ABE=∠ADC,∠ABD=∠ACD,
∴∠ACD=∠ADC,
∴AC=AD;
(2)证明:∵AE=AB,
∴∠E=∠ABE,
∵∠ABE=∠ADC,
∴∠E=∠ABE=∠ACD=∠ADC,
∴△AEB∽△ACD;
(3)解:由(2)知,△AEB∽△ACD,
∴
∵AC=AD=6,
∴,
∴CD==4.
21.(1);; (2);(3)的最小值
解:(1)如图,点O为等边△ABC外接圆的圆心,也是内切圆的圆心,作OD⊥AB于点D,连接OA,
∵等边三角形的边长AB为a,
∴AD=,
又∵∠DAO=∠BAC=60°×=30°,
∴.
∵DO为内切圆半径,
∴.
故答案为:a,a.
(2)∵△ABC为等边三角形,
∴AB=AC,∠C=∠CAB=60°,
又∵AE=CF,
在△ABE和△CAF中,
,
∴△ABE≌△CAF(SAS);
∴AF=BE,∠ABE=∠CAF.
又∵∠APE=∠BPF=∠ABP+∠BAP,
∴∠APE=∠BAP+∠CAF=60°.
∴∠APB=180°-∠APE=120°.
(3)CP存在最小值.
如图,过点A,点P,点B作⊙O,连接CO,PO,则点P在上运动,
∵AO=OP=OB,
∴∠OAP=∠OPA,∠OPB=∠OBP,∠OAB=∠OBA,
∴∠AOB=360°-∠OAP-∠OPA-∠OPB-∠OBP=120°,
∴∠OAB=30°,
∴∠CAO=90°,
∵AC=BC,OA=OB,
∴CO垂直平分AB,
∴∠ACO=30°,
∴cos∠ACO=,CO=2AO,
∴CO=4,
∴AO=2,
在△CPO中,CP≥CO-OP,
∴当点P在CO上时,CP有最小值,
∴CP的最小值=4-2=2,
22.(1);(2)
(1)
如图,连接,
,
∴CD:CA=CB:CD,
又,
,
,
、为半径
,
为的直径,
,
,
,
为的切线;
(2),是的切线,
,
,
,
,
,
设,则,,
在中,,
解得:,
.
