2021-2022学年人教版七年级数学上册第4章几何图形初步寒假自主提升测评 (Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版七年级数学上册第4章几何图形初步寒假自主提升测评 (Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 376.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-17 00:00:00 | ||
图片预览




文档简介
2021-2022学年人教版七年级数学上册《第4章几何图形初步》寒假自主提升测评(附答案)
一、单选题(满分40分)
1.“狂风四起,乌云密布.一霎时,雨点连成了线,……”这句话中蕴含的数学现象是( )
A.点动成线 B.线动成面 C.面动成体 D.雨下的大
2.下列两个生活、生产中现象:①用两个钉子就可以把木条固定在墙;②植树时,只要定出两棵树的位置就能确定同一行树所在直线;③从A地到B地架设电线总是尽可能沿着线段AB架设;④把弯曲的公路修直就能缩短路程.其中可以用“两点之间线段最短”来解释现象为( )
A.①② B.①③ C.②④ D.③④
3.已知点C是线段AB的中点,下列说法:①;②;③;④.其中正确的个数是( )
A.1 B.2 C.3 D.4
4.有5个大小一样的正方形制成如图所示的拼接图形(阴影部分),请你在图中的拼接图形上再拼接一个正方形,使新拼接成的图形折叠后能成为一个封闭的正方体盒子,在如图所示的A,B,C,D四个位置中,能够选择的位置有( )
A.1个 B.2个 C.3个 D.4个
5.由如图正方体的平面展开图可知,原正方体“建”字所在面的对面的汉字是( )
A.喜 B.党 C.百 D.年
6.钟表盘上指示的时间是11时20分,此刻时针与分针之间的夹角为( )
A. B. C. D.
7.如图,已知和都是直角,图中互补的角有( )对.
A.1 B.2 C.3 D.0
8.下面的几何体中,哪一个不能由平面图形绕某直线旋转一周得到( )
A. B. C. D.
9.下列几何体中,截面不可能是三角形的是( )
A.长方体 B.正方体 C.圆柱 D.圆锥
10.已知B,C,D三个车站的位置如图所示,B,C两站之间的距离是2a﹣b,B,D两站之间的距离是a﹣2b﹣1,则C,D两站之间的距离是( )
A.a﹣3b﹣1 B.a+b+1 C.a﹣b﹣1 D.a﹣3b﹣1
二、填空题(满分40分)
11.若一个直棱柱有8个顶点,且所有侧棱长的和为28cm,则每条侧棱长为_______cm.
12.如图是一个正方体的表面沿着某些棱剪开后展成的一个平面图形,若这个正方体的每两个相对面上的数字的和都是7,则x+y﹣z=_____.
13.已知与互为补角,且,则______.
14.如图,直线AB、CD相交于点O,OE⊥AB于点O,若∠COE=55°,则∠BOD为______.
15.如图,将三个同样的正方形的一个顶点重合放置,如果,时,那么的度数是___________度;
16.某种品牌牛奶包装盒的表面展开图如图所示(单位:),那么这种牛奶包装盒的体积是______(包装材料厚度不计)
17.已知图1的小正方形和图2中所有的小正方形边长都相等,将图1的小正方形安放在图2中的①、②、③、④的其中某一个位置,放置后所组成的图形是围成一个正方体的.那么安放的位置不是是__________.
18.在直线MN上取A、B两点,使AB=10cm,再在线段AB上取一点C,使AC=2cm,P、Q分别是AB、AC的中点,则PQ=___cm.
三、解答题(满分40分)
19.已知A、B、C在同一条直线上,且,其中点M是线段AB的中点,点N是线段BC的中点,求线段MN的长.
20.如图所示,一个几何体是由多个大小相同的小立方块搭成的,图中是从上面看到的图形,正方形中的数字表示在该位置小立方块的个数.请你画出从正面看和从左面看的这个几何体的形状图.
21.如图1,已知数轴上A,B两点表示的数分别为-9和7.
(1)AB= ;
(2)点P、点Q分别从点A、点B出发同时向右运动,点P的速度为每秒4个单位,点Q的速度为每秒2个单位,经过多少秒,点P与点Q相遇?
(3)如图2,线段AC的长度为3个单位,线段BD的长度为6个单位,线段AC以每秒4个单位的速度向右运动,同时线段BD以每秒2个单位的速度向左运动,设运动时间为t秒.
①t为何值时,点B恰好在线段AC的中点M处.
②t为何值时,AC的中点M与BD的中点N距离2个单位.
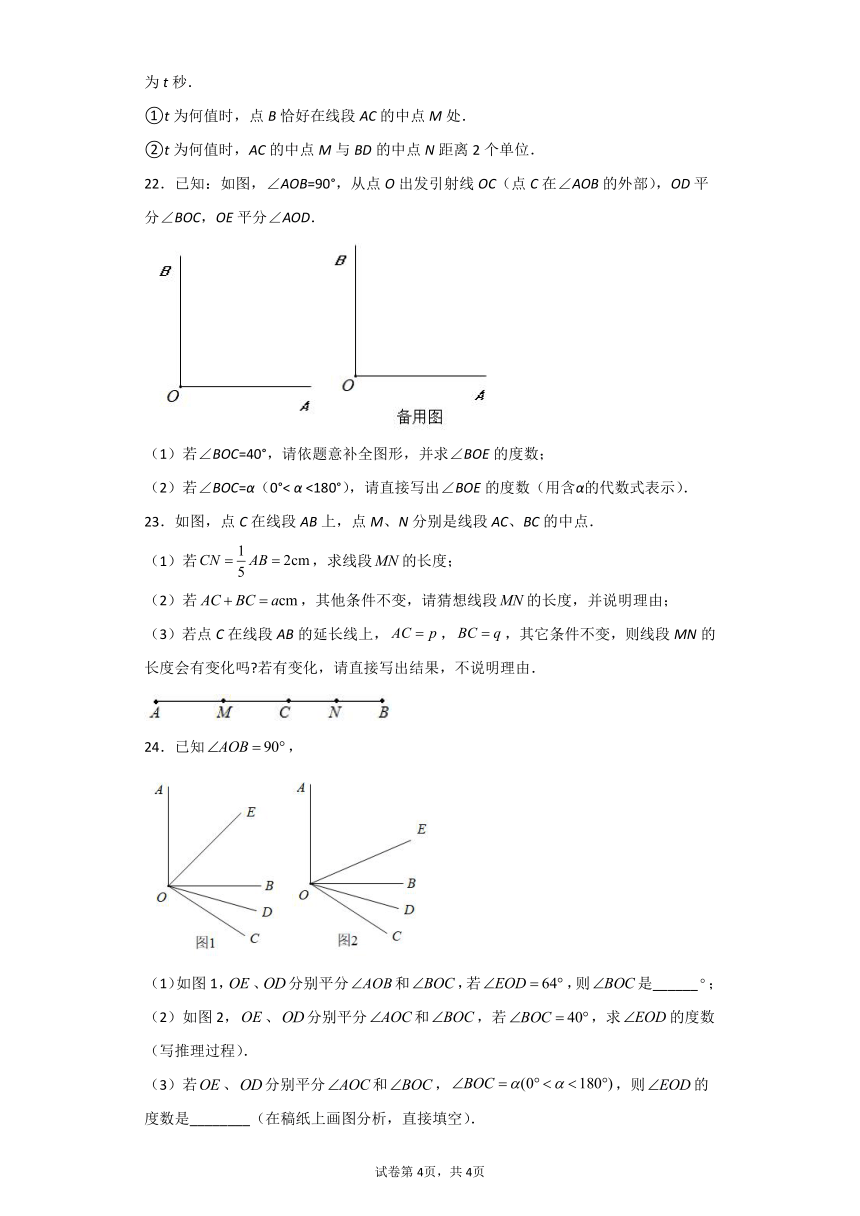
22.已知:如图,∠AOB=90°,从点O出发引射线OC(点C在∠AOB的外部),OD平分∠BOC,OE平分∠AOD.
(1)若∠BOC=40°,请依题意补全图形,并求∠BOE的度数;
(2)若∠BOC=α(0°< α <180°),请直接写出∠BOE的度数(用含α的代数式表示).
23.如图,点C在线段AB上,点M、N分别是线段AC、BC的中点.
(1)若,求线段的长度;
(2)若,其他条件不变,请猜想线段的长度,并说明理由;
(3)若点C在线段AB的延长线上,,,其它条件不变,则线段MN的长度会有变化吗 若有变化,请直接写出结果,不说明理由.
24.已知,
(1)如图1,、分别平分和,若,则是______;
(2)如图2,、分别平分和,若,求的度数(写推理过程).
(3)若、分别平分和,,则的度数是________(在稿纸上画图分析,直接填空).
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.A
解:雨点密集成一条直线,是点动成线的原理,
故选:A
2.D
解:①用两个钉子就可以把木条固定在墙上,②植树时,只要定出两棵树的位置,就能确定同一行树所在的直线的依据是“两点确定一条直线”;
③从A地到B地架设电线总是尽可能沿着线段AB架设;④把弯曲的公路修直就能缩短路程的依据是“两点之间线段最短”.
故选:D.
3.D
解:如图,点C是线段AB的中点,
故①,②,③,④都符合题意;
故选D
4.D
解:如图所示:
根据立方体的展开图可知,不能选择图中A的位置接正方形.
故选:C.
5.D
解:这是一个正方体的平面展开图,共有六个面,其中面“喜”与面“百”相对,面“迎”与面“党”相对,面“建”与面“年”相对.
故选:D
6.C
解:当钟表上显示11时20分时,分针指着4,时针处于11和12之间,走了11到12之间的 ,
由钟表的特点可知,每个大格是30°,如1到2,2到3都是30°,
故钟表上显示11时20分,则此刻时针与分针的夹角的度数为:4×30°+30°×=140°,
故答案为:C.
7.B
解:如图,延长BO至点E.
∵∠BOD=90°,
∴∠DOE=180° ∠DOB=90°.
∴∠DOE=∠DOB=∠AOC=90°.
∴∠AOC+∠BOD=180°,∠AOE+∠AOD=∠AOD+∠COD=∠DOC+∠BOC.
∴∠AOE=∠COD,∠AOD=∠BOC.
∵∠AOE+∠AOB=180°,
∴∠COD+∠AOB=180°.
综上:∠AOC与∠BOD互补,∠AOB与∠COD互补,共2对.
故选:B.
8.B
解:球可以由一个半圆绕直径所在的直线旋转一周得到,故A不符合题意;
正方体不能由一个平面图形绕某直线旋转一周得到,故B符合题意;
圆锥可以由一个直角三角形绕一条直角边所在的直线旋转一周得到,故C不符合题意;
圆柱可以由一个矩形绕一条边所在的直线旋转一周得到,故D不符合题意;故选B
9.C
解:A、长方体的截面可能是三角形,则此项不符题意;
B、正方体的截面可能是三角形,则此项不符题意;
C、圆柱的截面可能是圆形、长方形、梯形、椭圆形,不可能是三角形,则此项符合题意;
D、圆锥的截面可能是三角形,则此项不符题意;
故选:C.
10.C
解:
故选:C.
11.7
解:∵一个直棱柱有8个顶点,
∴上下两平面各有4个点,
∴该棱柱是四棱柱,它由四条侧棱,
∴它的每条侧棱长=28÷4=7cm.
故答案为:7.
12.-3
解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“2”与“z”是相对面,
“3”与“y”是相对面,
“x+4”与“5”是相对面,
∵这个正方体的每两个相对面上的数字的和都是7,
∴z=5,y=4,x=-2,
∴x+y-z=-2+4-5=-3.
故答案为:-3.
13.
解:∵与互为补角,
∴ ,
∵,
∴.
故答案为:
14.35°
解:∵OE⊥AB,
∴∠AOE=90°,
∵ ,
∴∠AOC=90°- ,
∴∠BOD=∠AOC= ,
故答案为:35°.
15.27
解:如图,由题意得:,
由②和③得:,
将代入①得:,
解得,
故答案为:27.
16.224000
解:包装盒的底面积为40×70=2800mm2,包装盒的高为80mm,
这种牛奶包装盒的体积是2800×80=224000.
故答案为224000.
17.①
解:将图1的正方形放在图2中的①的位置出现重叠的面,所以不能围成正方体.
故答案为:①.
18.4如图,
∵AB=10, AC=2cm,P、Q分别是AB、AC的中点,
∴AP= AB=5,AQ= AC=1,
∴PQ=AP-AQ
=5-1
=4,
故答案为:4.
19.4cm或8cm
解:(1)点C在线段AB上时,如图
∵M、N分别是线段AB、BC的中点,且AB=12cm,BC=4cm
∴,
∴;
(2)点C在线段AB的延长线上时,如图
∴
所以线段MN的长为4cm或8cm.
20.解:如图所示:
21.(1);(2)经过秒,点P与点Q相遇;(3)①当秒,点B恰好在线段AC的中点M处;②当或时,AC的中点M与BD的中点N距离2个单位
解:(1)数轴上A,B两点表示的数分别为-9和7
所以,
故答案为:
(2)设时间为秒,则点表示的数为,点表示的数为
由题意可得:
解得
即经过秒,点P与点Q相遇;
(3)①运动时间为秒时,点表示的数为,点表示的数为,
点表示的数为,点表示的数为
点为线段的中点,
∴点表示的数为
由题意可得:,解得
即当秒,点B恰好在线段AC的中点M处;
②点为线段的中点,
点表示的数为
由题意可得:,即
即或
解得或,
即当或时,AC的中点M与BD的中点N距离2个单位.
22.(1);(2)或
解:(1)∵,
∴,
∵ ,
∴ ,
∵ ,
∴ ,
∴ ;
(2)如图OC在直线OB左侧,
∵OD平分∠BOC,
∴∠BOD=,
∴∠AOD=∠BOD+∠AOB=90°+,
∵OE平分∠AOD,
∴∠DOE=,
∴;
OC在直线OB右侧,
∵OD平分∠BOC,
∴∠BOD=,
∴∠AOD=∠BOD-∠AOB=90°-,
∵OE平分∠AOD,
∴∠DOE=,
∴;
综合∠BOE的度数为或.
23.(1)5cm;(2);(3)无变化,MN=
解:(1)∵,
∴AB=10cm,
∵点M、N分别是线段AC、BC的中点,
∴CN=BC,CM=AC,
∴MN=CM+CN=CN= AC+BC=(AC+BC)=AB=5cm;
(2)MN=,理由:
∵点M、N分别是线段AC、BC的中点,
∴CN=BC,CM=AC,
∵AB=acm,
∴MN=CM+CN=CN= AC+BC=(AC+BC)=AB=cm;
(3)无变化,MN=,理由:
如图,
∵点M、N分别是线段AC、BC的中点,
∴CN=BC,CM=AC,
∵,,
∴MN=CM-CN= AC-BC=(AC-BC)=;
24.(1)38;(2);(3)45°或135°
解:(1)∵,OE平分,
∴,
∵,
∴,
∵OD平分,
∴,
故答案为:38;
(2)∵OD平分,,,
∴,,
∵OE平分,
∴,
∴;
(3)如图3所示,当OE,OD都在∠AOB外部时,
∵OE,OD分别平分∠AOC,∠BOC,
∴,,
∴,
∵,
∴,
∴,
∴;
当如图1所示,DE在∠AOB内部,OD在∠AOB外部时,
由(2)可知此时
如图所示,当OD在∠AOB内部,OE在∠AOB外部时,
∵OE,OD分别平分∠AOC,∠BOC,
∴,,
∵,,
∴,
∴,
∴;
如图5所示,当OD,OE都在∠AOB内部时,
同理可得,,
∵,,
∴,
∴,
∴;
∴综上所述,或,
故答案为:45°或135°.
一、单选题(满分40分)
1.“狂风四起,乌云密布.一霎时,雨点连成了线,……”这句话中蕴含的数学现象是( )
A.点动成线 B.线动成面 C.面动成体 D.雨下的大
2.下列两个生活、生产中现象:①用两个钉子就可以把木条固定在墙;②植树时,只要定出两棵树的位置就能确定同一行树所在直线;③从A地到B地架设电线总是尽可能沿着线段AB架设;④把弯曲的公路修直就能缩短路程.其中可以用“两点之间线段最短”来解释现象为( )
A.①② B.①③ C.②④ D.③④
3.已知点C是线段AB的中点,下列说法:①;②;③;④.其中正确的个数是( )
A.1 B.2 C.3 D.4
4.有5个大小一样的正方形制成如图所示的拼接图形(阴影部分),请你在图中的拼接图形上再拼接一个正方形,使新拼接成的图形折叠后能成为一个封闭的正方体盒子,在如图所示的A,B,C,D四个位置中,能够选择的位置有( )
A.1个 B.2个 C.3个 D.4个
5.由如图正方体的平面展开图可知,原正方体“建”字所在面的对面的汉字是( )
A.喜 B.党 C.百 D.年
6.钟表盘上指示的时间是11时20分,此刻时针与分针之间的夹角为( )
A. B. C. D.
7.如图,已知和都是直角,图中互补的角有( )对.
A.1 B.2 C.3 D.0
8.下面的几何体中,哪一个不能由平面图形绕某直线旋转一周得到( )
A. B. C. D.
9.下列几何体中,截面不可能是三角形的是( )
A.长方体 B.正方体 C.圆柱 D.圆锥
10.已知B,C,D三个车站的位置如图所示,B,C两站之间的距离是2a﹣b,B,D两站之间的距离是a﹣2b﹣1,则C,D两站之间的距离是( )
A.a﹣3b﹣1 B.a+b+1 C.a﹣b﹣1 D.a﹣3b﹣1
二、填空题(满分40分)
11.若一个直棱柱有8个顶点,且所有侧棱长的和为28cm,则每条侧棱长为_______cm.
12.如图是一个正方体的表面沿着某些棱剪开后展成的一个平面图形,若这个正方体的每两个相对面上的数字的和都是7,则x+y﹣z=_____.
13.已知与互为补角,且,则______.
14.如图,直线AB、CD相交于点O,OE⊥AB于点O,若∠COE=55°,则∠BOD为______.
15.如图,将三个同样的正方形的一个顶点重合放置,如果,时,那么的度数是___________度;
16.某种品牌牛奶包装盒的表面展开图如图所示(单位:),那么这种牛奶包装盒的体积是______(包装材料厚度不计)
17.已知图1的小正方形和图2中所有的小正方形边长都相等,将图1的小正方形安放在图2中的①、②、③、④的其中某一个位置,放置后所组成的图形是围成一个正方体的.那么安放的位置不是是__________.
18.在直线MN上取A、B两点,使AB=10cm,再在线段AB上取一点C,使AC=2cm,P、Q分别是AB、AC的中点,则PQ=___cm.
三、解答题(满分40分)
19.已知A、B、C在同一条直线上,且,其中点M是线段AB的中点,点N是线段BC的中点,求线段MN的长.
20.如图所示,一个几何体是由多个大小相同的小立方块搭成的,图中是从上面看到的图形,正方形中的数字表示在该位置小立方块的个数.请你画出从正面看和从左面看的这个几何体的形状图.
21.如图1,已知数轴上A,B两点表示的数分别为-9和7.
(1)AB= ;
(2)点P、点Q分别从点A、点B出发同时向右运动,点P的速度为每秒4个单位,点Q的速度为每秒2个单位,经过多少秒,点P与点Q相遇?
(3)如图2,线段AC的长度为3个单位,线段BD的长度为6个单位,线段AC以每秒4个单位的速度向右运动,同时线段BD以每秒2个单位的速度向左运动,设运动时间为t秒.
①t为何值时,点B恰好在线段AC的中点M处.
②t为何值时,AC的中点M与BD的中点N距离2个单位.
22.已知:如图,∠AOB=90°,从点O出发引射线OC(点C在∠AOB的外部),OD平分∠BOC,OE平分∠AOD.
(1)若∠BOC=40°,请依题意补全图形,并求∠BOE的度数;
(2)若∠BOC=α(0°< α <180°),请直接写出∠BOE的度数(用含α的代数式表示).
23.如图,点C在线段AB上,点M、N分别是线段AC、BC的中点.
(1)若,求线段的长度;
(2)若,其他条件不变,请猜想线段的长度,并说明理由;
(3)若点C在线段AB的延长线上,,,其它条件不变,则线段MN的长度会有变化吗 若有变化,请直接写出结果,不说明理由.
24.已知,
(1)如图1,、分别平分和,若,则是______;
(2)如图2,、分别平分和,若,求的度数(写推理过程).
(3)若、分别平分和,,则的度数是________(在稿纸上画图分析,直接填空).
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.A
解:雨点密集成一条直线,是点动成线的原理,
故选:A
2.D
解:①用两个钉子就可以把木条固定在墙上,②植树时,只要定出两棵树的位置,就能确定同一行树所在的直线的依据是“两点确定一条直线”;
③从A地到B地架设电线总是尽可能沿着线段AB架设;④把弯曲的公路修直就能缩短路程的依据是“两点之间线段最短”.
故选:D.
3.D
解:如图,点C是线段AB的中点,
故①,②,③,④都符合题意;
故选D
4.D
解:如图所示:
根据立方体的展开图可知,不能选择图中A的位置接正方形.
故选:C.
5.D
解:这是一个正方体的平面展开图,共有六个面,其中面“喜”与面“百”相对,面“迎”与面“党”相对,面“建”与面“年”相对.
故选:D
6.C
解:当钟表上显示11时20分时,分针指着4,时针处于11和12之间,走了11到12之间的 ,
由钟表的特点可知,每个大格是30°,如1到2,2到3都是30°,
故钟表上显示11时20分,则此刻时针与分针的夹角的度数为:4×30°+30°×=140°,
故答案为:C.
7.B
解:如图,延长BO至点E.
∵∠BOD=90°,
∴∠DOE=180° ∠DOB=90°.
∴∠DOE=∠DOB=∠AOC=90°.
∴∠AOC+∠BOD=180°,∠AOE+∠AOD=∠AOD+∠COD=∠DOC+∠BOC.
∴∠AOE=∠COD,∠AOD=∠BOC.
∵∠AOE+∠AOB=180°,
∴∠COD+∠AOB=180°.
综上:∠AOC与∠BOD互补,∠AOB与∠COD互补,共2对.
故选:B.
8.B
解:球可以由一个半圆绕直径所在的直线旋转一周得到,故A不符合题意;
正方体不能由一个平面图形绕某直线旋转一周得到,故B符合题意;
圆锥可以由一个直角三角形绕一条直角边所在的直线旋转一周得到,故C不符合题意;
圆柱可以由一个矩形绕一条边所在的直线旋转一周得到,故D不符合题意;故选B
9.C
解:A、长方体的截面可能是三角形,则此项不符题意;
B、正方体的截面可能是三角形,则此项不符题意;
C、圆柱的截面可能是圆形、长方形、梯形、椭圆形,不可能是三角形,则此项符合题意;
D、圆锥的截面可能是三角形,则此项不符题意;
故选:C.
10.C
解:
故选:C.
11.7
解:∵一个直棱柱有8个顶点,
∴上下两平面各有4个点,
∴该棱柱是四棱柱,它由四条侧棱,
∴它的每条侧棱长=28÷4=7cm.
故答案为:7.
12.-3
解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“2”与“z”是相对面,
“3”与“y”是相对面,
“x+4”与“5”是相对面,
∵这个正方体的每两个相对面上的数字的和都是7,
∴z=5,y=4,x=-2,
∴x+y-z=-2+4-5=-3.
故答案为:-3.
13.
解:∵与互为补角,
∴ ,
∵,
∴.
故答案为:
14.35°
解:∵OE⊥AB,
∴∠AOE=90°,
∵ ,
∴∠AOC=90°- ,
∴∠BOD=∠AOC= ,
故答案为:35°.
15.27
解:如图,由题意得:,
由②和③得:,
将代入①得:,
解得,
故答案为:27.
16.224000
解:包装盒的底面积为40×70=2800mm2,包装盒的高为80mm,
这种牛奶包装盒的体积是2800×80=224000.
故答案为224000.
17.①
解:将图1的正方形放在图2中的①的位置出现重叠的面,所以不能围成正方体.
故答案为:①.
18.4如图,
∵AB=10, AC=2cm,P、Q分别是AB、AC的中点,
∴AP= AB=5,AQ= AC=1,
∴PQ=AP-AQ
=5-1
=4,
故答案为:4.
19.4cm或8cm
解:(1)点C在线段AB上时,如图
∵M、N分别是线段AB、BC的中点,且AB=12cm,BC=4cm
∴,
∴;
(2)点C在线段AB的延长线上时,如图
∴
所以线段MN的长为4cm或8cm.
20.解:如图所示:
21.(1);(2)经过秒,点P与点Q相遇;(3)①当秒,点B恰好在线段AC的中点M处;②当或时,AC的中点M与BD的中点N距离2个单位
解:(1)数轴上A,B两点表示的数分别为-9和7
所以,
故答案为:
(2)设时间为秒,则点表示的数为,点表示的数为
由题意可得:
解得
即经过秒,点P与点Q相遇;
(3)①运动时间为秒时,点表示的数为,点表示的数为,
点表示的数为,点表示的数为
点为线段的中点,
∴点表示的数为
由题意可得:,解得
即当秒,点B恰好在线段AC的中点M处;
②点为线段的中点,
点表示的数为
由题意可得:,即
即或
解得或,
即当或时,AC的中点M与BD的中点N距离2个单位.
22.(1);(2)或
解:(1)∵,
∴,
∵ ,
∴ ,
∵ ,
∴ ,
∴ ;
(2)如图OC在直线OB左侧,
∵OD平分∠BOC,
∴∠BOD=,
∴∠AOD=∠BOD+∠AOB=90°+,
∵OE平分∠AOD,
∴∠DOE=,
∴;
OC在直线OB右侧,
∵OD平分∠BOC,
∴∠BOD=,
∴∠AOD=∠BOD-∠AOB=90°-,
∵OE平分∠AOD,
∴∠DOE=,
∴;
综合∠BOE的度数为或.
23.(1)5cm;(2);(3)无变化,MN=
解:(1)∵,
∴AB=10cm,
∵点M、N分别是线段AC、BC的中点,
∴CN=BC,CM=AC,
∴MN=CM+CN=CN= AC+BC=(AC+BC)=AB=5cm;
(2)MN=,理由:
∵点M、N分别是线段AC、BC的中点,
∴CN=BC,CM=AC,
∵AB=acm,
∴MN=CM+CN=CN= AC+BC=(AC+BC)=AB=cm;
(3)无变化,MN=,理由:
如图,
∵点M、N分别是线段AC、BC的中点,
∴CN=BC,CM=AC,
∵,,
∴MN=CM-CN= AC-BC=(AC-BC)=;
24.(1)38;(2);(3)45°或135°
解:(1)∵,OE平分,
∴,
∵,
∴,
∵OD平分,
∴,
故答案为:38;
(2)∵OD平分,,,
∴,,
∵OE平分,
∴,
∴;
(3)如图3所示,当OE,OD都在∠AOB外部时,
∵OE,OD分别平分∠AOC,∠BOC,
∴,,
∴,
∵,
∴,
∴,
∴;
当如图1所示,DE在∠AOB内部,OD在∠AOB外部时,
由(2)可知此时
如图所示,当OD在∠AOB内部,OE在∠AOB外部时,
∵OE,OD分别平分∠AOC,∠BOC,
∴,,
∵,,
∴,
∴,
∴;
如图5所示,当OD,OE都在∠AOB内部时,
同理可得,,
∵,,
∴,
∴,
∴;
∴综上所述,或,
故答案为:45°或135°.
