人教高中数学必修三3.3.1几何概型 课件(24张ppt)
文档属性
| 名称 | 人教高中数学必修三3.3.1几何概型 课件(24张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-18 18:07:55 | ||
图片预览






文档简介
(共24张PPT)
(1)试验中所有可能出现的基本事件
是有限个;
(2)每个基本事件出现的可能性相等。
回顾:
P(A)=
总的基本事件个数
A包含的基本事件个数
古典概型的特点及公式:
《凉凉》歌曲全长4分钟,高潮部分从第50秒末开始,到第1分30秒末结束.暑假中的一天,他正戴着耳机以单曲循环的播放模式听《凉凉》.这时,妈妈喊他有事.回来后,他又立刻戴上耳机.
请问:小明恰好听到《凉凉》高潮部分的概率是多少?
几何概型
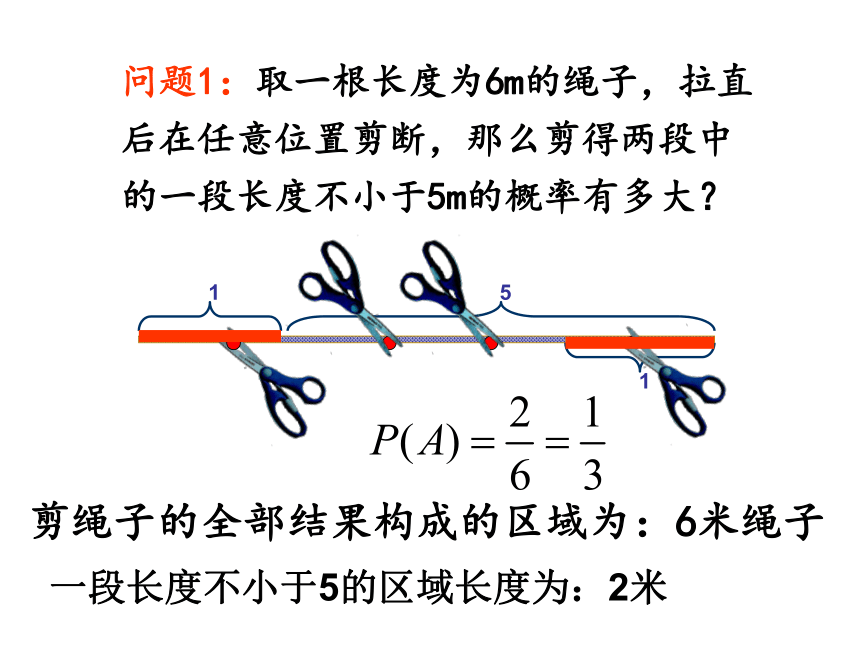
问题1:取一根长度为6m的绳子,拉直后在任意位置剪断,那么剪得两段中的一段长度不小于5m的概率有多大?
剪绳子的全部结果构成的区域为:6米绳子
1
5
1
一段长度不小于5的区域长度为:2米
探究规律:
几何概型公式(1):
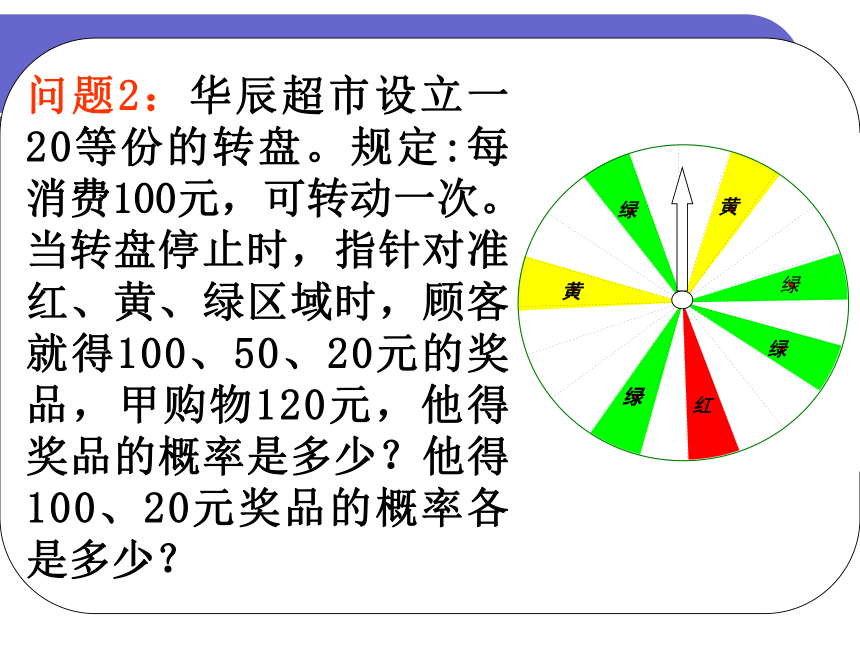
问题2:华辰超市设立一20等份的转盘。规定:每消费100元,可转动一次。当转盘停止时,指针对准红、黄、绿区域时,顾客就得100、50、20元的奖品,甲购物120元,他得奖品的概率是多少?他得100、20元奖品的概率各是多少?
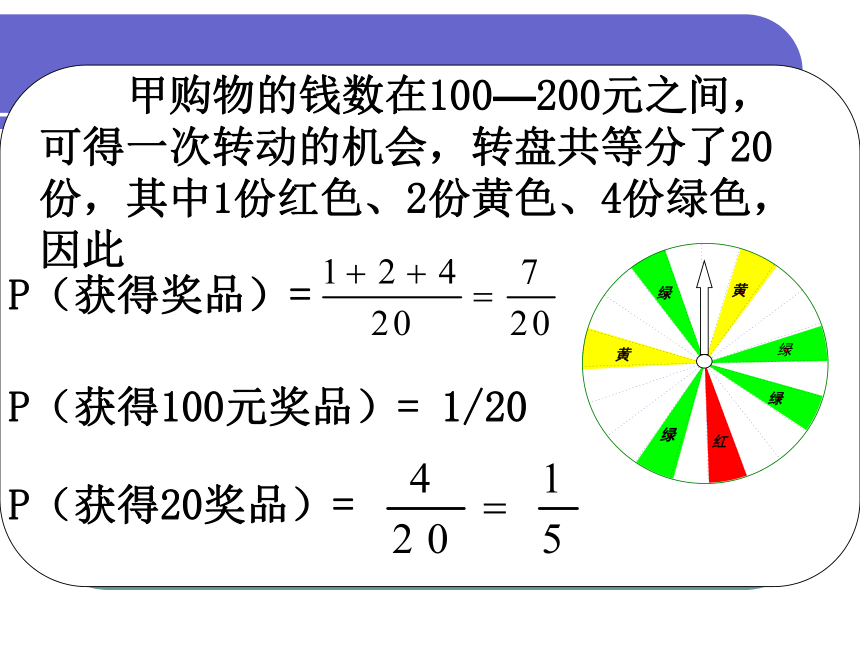
甲购物的钱数在100—200元之间,可得一次转动的机会,转盘共等分了20份,其中1份红色、2份黄色、4份绿色,因此
P(获得奖品)=
P(获得100元奖品)= 1/20
P(获得20奖品)=
探究规律:
几何概型公式(2):
问题3:一只小蜜蜂在一个棱长为3的正方体内自由飞行,若蜜蜂在飞行过程中始终保持与正方体6个面的距离均大于1,称其为“安全飞行”,求蜜蜂“安全飞行”的概率.
变式探究:本例条件不变,求这个蜜蜂飞到正方体某一顶点A的距离小于1的概率.
探究规律:
几何概型公式(3):
1、在等腰直角三角形ABC中,
(1)在斜边AB上任取一点D,则AD(2)过直角顶点C在∠ACB内部作一条射线CM,与线段AB交于点M,求AM问题4:
探究规律:
几何概型公式(4):
试验的全部结果所构成的区域长度(面积或体积或角度)
P(A)=
构成事件A的区域长度(面积或体积或角度)
归纳:几何概型定特点及事件A的概率计算公式:
特点:事件中所有可能出现的结果(基本事件)无限个
每个事件出现的可能性相同
余则成按组织要求每晚整点收听广播指令,且每小时重播一次,则他晚上打开广播等候不超过10分钟即能收听指令的概率是多少?
例题1:
解:设A={等候的时间不超过10分钟},能收听指令应在[50,60]时间段内,由几何概型公式得:
夜华与白浅约定6时到7时之间在某处会面,为确保不让其他人看见,约定先到者等候另一人一刻钟,过时即可离去,求两人能会面的概率.
例题2:
.M(X,Y)
解:以 X , Y 分别表示夜、白二人到达的时刻,于是
y
7
6
0 6 7
x
会面的条件是:
y
7
6
0 6 7
x
则二人能在6点至7点会面的概率是
会面的条件是:
解:以 X , Y 分别表示夜、白二人到达的时刻,于是
解析:当以O为圆心,1为半径的圆,则圆与长方形的公共区域内的点满足到点O的距离小于或等于1,故所求事件的概率为
A
B
C
D
O
选B
几何概型的基本题型:
总结:
利用长度比值求概率;
利用面积的比值求概率;
(注意与线性规划的结合)
利用体积的比值求概率;
利用角度的比值求概率
思想方法:
建模思想
转化与化归思想
解题步骤:
分清类型(古典、几何)
明确事件(基本事件)
选择公式
解决概率有关问题的体会:
数学来源于生活
应用于生活
半径为2的圆内有一点A,现在随机向圆内扔一颗小豆子,
(1)求豆子落点正好为点A的概率。(2)求豆子落点不为点A的概率。
结论:1、若A是不可能事件P(A)=0
反之不成立
2、若A是必然事件 P(A)=1
反之不成立
思考:
A
(1)试验中所有可能出现的基本事件
是有限个;
(2)每个基本事件出现的可能性相等。
回顾:
P(A)=
总的基本事件个数
A包含的基本事件个数
古典概型的特点及公式:
《凉凉》歌曲全长4分钟,高潮部分从第50秒末开始,到第1分30秒末结束.暑假中的一天,他正戴着耳机以单曲循环的播放模式听《凉凉》.这时,妈妈喊他有事.回来后,他又立刻戴上耳机.
请问:小明恰好听到《凉凉》高潮部分的概率是多少?
几何概型
问题1:取一根长度为6m的绳子,拉直后在任意位置剪断,那么剪得两段中的一段长度不小于5m的概率有多大?
剪绳子的全部结果构成的区域为:6米绳子
1
5
1
一段长度不小于5的区域长度为:2米
探究规律:
几何概型公式(1):
问题2:华辰超市设立一20等份的转盘。规定:每消费100元,可转动一次。当转盘停止时,指针对准红、黄、绿区域时,顾客就得100、50、20元的奖品,甲购物120元,他得奖品的概率是多少?他得100、20元奖品的概率各是多少?
甲购物的钱数在100—200元之间,可得一次转动的机会,转盘共等分了20份,其中1份红色、2份黄色、4份绿色,因此
P(获得奖品)=
P(获得100元奖品)= 1/20
P(获得20奖品)=
探究规律:
几何概型公式(2):
问题3:一只小蜜蜂在一个棱长为3的正方体内自由飞行,若蜜蜂在飞行过程中始终保持与正方体6个面的距离均大于1,称其为“安全飞行”,求蜜蜂“安全飞行”的概率.
变式探究:本例条件不变,求这个蜜蜂飞到正方体某一顶点A的距离小于1的概率.
探究规律:
几何概型公式(3):
1、在等腰直角三角形ABC中,
(1)在斜边AB上任取一点D,则AD
探究规律:
几何概型公式(4):
试验的全部结果所构成的区域长度(面积或体积或角度)
P(A)=
构成事件A的区域长度(面积或体积或角度)
归纳:几何概型定特点及事件A的概率计算公式:
特点:事件中所有可能出现的结果(基本事件)无限个
每个事件出现的可能性相同
余则成按组织要求每晚整点收听广播指令,且每小时重播一次,则他晚上打开广播等候不超过10分钟即能收听指令的概率是多少?
例题1:
解:设A={等候的时间不超过10分钟},能收听指令应在[50,60]时间段内,由几何概型公式得:
夜华与白浅约定6时到7时之间在某处会面,为确保不让其他人看见,约定先到者等候另一人一刻钟,过时即可离去,求两人能会面的概率.
例题2:
.M(X,Y)
解:以 X , Y 分别表示夜、白二人到达的时刻,于是
y
7
6
0 6 7
x
会面的条件是:
y
7
6
0 6 7
x
则二人能在6点至7点会面的概率是
会面的条件是:
解:以 X , Y 分别表示夜、白二人到达的时刻,于是
解析:当以O为圆心,1为半径的圆,则圆与长方形的公共区域内的点满足到点O的距离小于或等于1,故所求事件的概率为
A
B
C
D
O
选B
几何概型的基本题型:
总结:
利用长度比值求概率;
利用面积的比值求概率;
(注意与线性规划的结合)
利用体积的比值求概率;
利用角度的比值求概率
思想方法:
建模思想
转化与化归思想
解题步骤:
分清类型(古典、几何)
明确事件(基本事件)
选择公式
解决概率有关问题的体会:
数学来源于生活
应用于生活
半径为2的圆内有一点A,现在随机向圆内扔一颗小豆子,
(1)求豆子落点正好为点A的概率。(2)求豆子落点不为点A的概率。
结论:1、若A是不可能事件P(A)=0
反之不成立
2、若A是必然事件 P(A)=1
反之不成立
思考:
A
