人教高中数学必修三2.2.2用样本的数字特征估计总体的数字特征 (一)众数、中位数、平均数 课件(16张ppt)
文档属性
| 名称 | 人教高中数学必修三2.2.2用样本的数字特征估计总体的数字特征 (一)众数、中位数、平均数 课件(16张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 204.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-18 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
(一)众数、中位数、平均数
2.2.2
用样本的数字特征估计
总体的数字特征
学习目标:
1、理解众数、中位数、平均数在样本数据中所代表的含义;
2、会运用频率分布直方图估计众数、中位数、平均数;
3、理解在利用众数、中位数、平均数估计总体的数字特征时各自的优缺点;
教学重点:
如何从样本频率分布直方图中估计众数、中位数、平均数
教学难点:
从频率分布图中估计出中位数
复习回顾:众数、中位数和平均数
思考1:在初中我们学过众数、中位数和平均数的概念,这些数据都是反映样本信息的数字特征,对一组样本数据如何求众数、中位数和平均数?
思考2:众数,中位数,平均数的特点是什么
1、求下列各组数据的众数
(1)1 ,2,3,3,3,5,5,8,8,8,9,9
(2)1 ,2,3,3,3,5,5,8,8,9,9
(3) 1, 2, 3, 4, 5
2、求下列各组数据的中位数
(1)1 ,2,3,3,3,4,6,8,8,8,9,9
(2)1 ,2,3,3,3,4,8,8,8,9,9
3、求下列各组数据的平均数
(1)1 ,9,3,7,6,4,2,8,
(2)1 ,1,3,7,6,4,2,8,
(3) 101,102,98,105,99
脱口而出
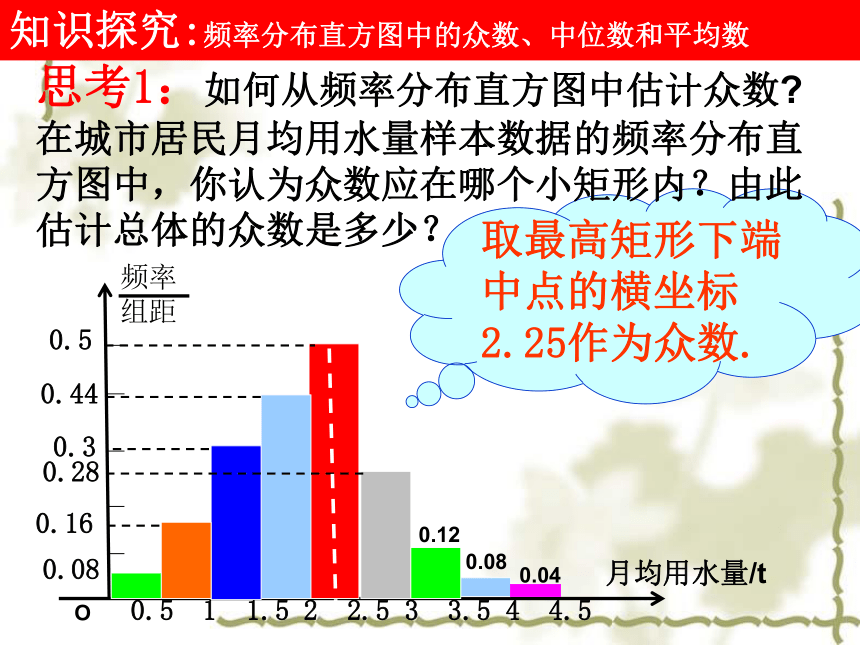
取最高矩形下端中点的横坐标2.25作为众数.
思考1:如何从频率分布直方图中估计众数 在城市居民月均用水量样本数据的频率分布直方图中,你认为众数应在哪个小矩形内?由此估计总体的众数是多少?
知识探究:频率分布直方图中的众数、中位数和平均数
0.16
0.5 1 1.5 2 2.5 3 3.5 4 4.5
月均用水量/t
频率
组距
0.08
O
0.3
0.44
0.5
0.28
0.12
0.08
0.04
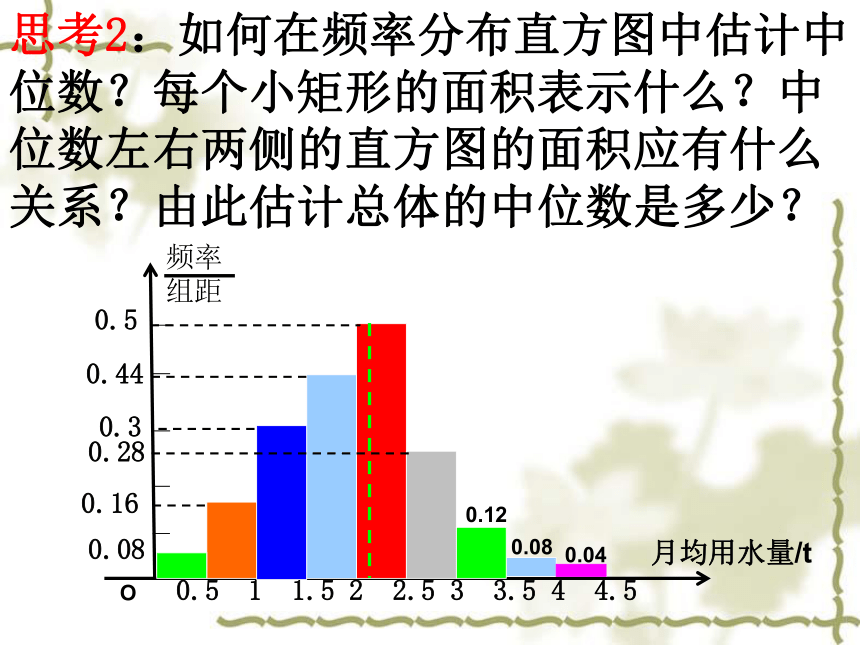
思考2:如何在频率分布直方图中估计中位数?每个小矩形的面积表示什么?中位数左右两侧的直方图的面积应有什么关系?由此估计总体的中位数是多少?
0.16
0.5 1 1.5 2 2.5 3 3.5 4 4.5
月均用水量/t
频率
组距
0.08
O
0.3
0.44
0.5
0.28
0.12
0.08
0.04
0.5
2.5
2
1.5
1
4
3.5
3
4.5
频率
组距
0.04
0.08
0.15
0.22
0.25
0.14
0.06
0.04
0.02
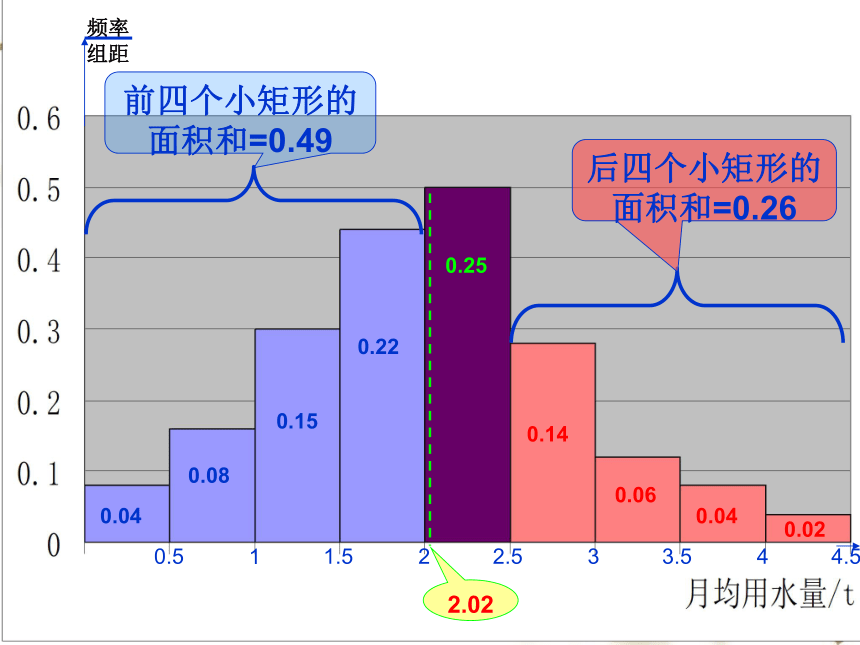
前四个小矩形的面积和=0.49
后四个小矩形的面积和=0.26
2.02
思考3:如何在频率分布直方图中估计平均数?平均数是频率分布直方图的“重心”,各个小矩形的重心在哪里?总体在各组数据内的平均数分别为多少?由此估计总体的平均数是多少?
0.16
0.5 1 1.5 2 2.5 3 3.5 4 4.5
月均用水量/t
频率
组距
0.08
O
0.3
0.44
0.5
0.28
0.12
0.08
0.04
问题1:请大家翻回到课本看看原来抽样的数据,从居民月均用水量样本数据可知,该样本的众数是2.3,中位数是2.0,平均数是1.973,这与我们从样本频率分布直方图得出的结论有偏差,你能解释一下原因吗?
问题2: 中位数不受少数几个极端值的影响,这在某些情况下是一个优点,但是它对极端值的不敏感有时也会成为缺点,你能举例说明吗?
问题3: 在体育、文艺等各种比赛的评分中,使用的是平均数.计分过程中采用“去掉一个最高分,去掉一个最低分”的方法,说说这种方法的好处。
问题4:书本73页的探究如何理解?
问题5: 总结在利用众数、中位数、平均数估计总体的数字特征时各自的优缺点。
课中反思:
三种数字特征的优缺点
特征数 优 点 缺 点
众数 容易计算,体现了样本数据的最大集中点 无法客观反映总体特征,只能表示样本数据中的很少一部分信息,不一定唯一。
中位数 不受少数极端值的影响 中位数仅利用了数据中排在中间数据的信息,与数据的排列位置有关
平均数 与每一个数据有关,更能反映全体的信息 受每个样本数据的影响,使其在估计总体时的可靠性降低.
[例] 某中学举行电脑知识竞赛,现将高一参赛学生的成绩进行整理后分成五组绘制成如图所示的频率分布直方图,
求:高一参赛学生的成绩的众数、中位数及平均成绩.
典例解析
1.数据:1,1,3,3的众数和中位数分别是 ( )
A.1和3,2 B.3,2
C.1和3,1和3 D.3,3
2.频率分布直方图中最高小矩形的中间位置所对的数字特征是( )
A.中位数 B.众数
C.平均数 D.标准差
当堂训练
90
100
110
120
130
140
150
次数
0
0.004
0.008
0.012
0.01
0.020
0.024
0.028
频率/组距
0.032
0.036
3.为了了解高一学生的体能情况,某校抽取部分学生进行
一分钟跳绳次数次测试,将所得数据整理后,画出频率
分布直方图,图中从左到右各小长方形面积之比为
2:4:17:15:9:3,第二小组频数为12.
(1)第二小组的频率是多少?
样本容量是多少?
(2)在这次测试中,
学生跳绳次数的中位
数落在哪个小组内?
请说明理由
众数:最高矩形的中点的横坐标。
中位数:两边小长方形面积相等
平均数:频率分布直方图中每个小矩形的面积乘以小矩形底边中点的横坐标之和。
课堂小结
1、如何从样本数据中求众数、平均数、中位数的方法
2、如何从频率分布直方图中估计众数、中位数、平均数?
课本79页3题
习题2.2A组1,5,6,7
作业布置
谢谢大家
感谢各位领导和老师们的
指导,请多提宝贵意见!
(一)众数、中位数、平均数
2.2.2
用样本的数字特征估计
总体的数字特征
学习目标:
1、理解众数、中位数、平均数在样本数据中所代表的含义;
2、会运用频率分布直方图估计众数、中位数、平均数;
3、理解在利用众数、中位数、平均数估计总体的数字特征时各自的优缺点;
教学重点:
如何从样本频率分布直方图中估计众数、中位数、平均数
教学难点:
从频率分布图中估计出中位数
复习回顾:众数、中位数和平均数
思考1:在初中我们学过众数、中位数和平均数的概念,这些数据都是反映样本信息的数字特征,对一组样本数据如何求众数、中位数和平均数?
思考2:众数,中位数,平均数的特点是什么
1、求下列各组数据的众数
(1)1 ,2,3,3,3,5,5,8,8,8,9,9
(2)1 ,2,3,3,3,5,5,8,8,9,9
(3) 1, 2, 3, 4, 5
2、求下列各组数据的中位数
(1)1 ,2,3,3,3,4,6,8,8,8,9,9
(2)1 ,2,3,3,3,4,8,8,8,9,9
3、求下列各组数据的平均数
(1)1 ,9,3,7,6,4,2,8,
(2)1 ,1,3,7,6,4,2,8,
(3) 101,102,98,105,99
脱口而出
取最高矩形下端中点的横坐标2.25作为众数.
思考1:如何从频率分布直方图中估计众数 在城市居民月均用水量样本数据的频率分布直方图中,你认为众数应在哪个小矩形内?由此估计总体的众数是多少?
知识探究:频率分布直方图中的众数、中位数和平均数
0.16
0.5 1 1.5 2 2.5 3 3.5 4 4.5
月均用水量/t
频率
组距
0.08
O
0.3
0.44
0.5
0.28
0.12
0.08
0.04
思考2:如何在频率分布直方图中估计中位数?每个小矩形的面积表示什么?中位数左右两侧的直方图的面积应有什么关系?由此估计总体的中位数是多少?
0.16
0.5 1 1.5 2 2.5 3 3.5 4 4.5
月均用水量/t
频率
组距
0.08
O
0.3
0.44
0.5
0.28
0.12
0.08
0.04
0.5
2.5
2
1.5
1
4
3.5
3
4.5
频率
组距
0.04
0.08
0.15
0.22
0.25
0.14
0.06
0.04
0.02
前四个小矩形的面积和=0.49
后四个小矩形的面积和=0.26
2.02
思考3:如何在频率分布直方图中估计平均数?平均数是频率分布直方图的“重心”,各个小矩形的重心在哪里?总体在各组数据内的平均数分别为多少?由此估计总体的平均数是多少?
0.16
0.5 1 1.5 2 2.5 3 3.5 4 4.5
月均用水量/t
频率
组距
0.08
O
0.3
0.44
0.5
0.28
0.12
0.08
0.04
问题1:请大家翻回到课本看看原来抽样的数据,从居民月均用水量样本数据可知,该样本的众数是2.3,中位数是2.0,平均数是1.973,这与我们从样本频率分布直方图得出的结论有偏差,你能解释一下原因吗?
问题2: 中位数不受少数几个极端值的影响,这在某些情况下是一个优点,但是它对极端值的不敏感有时也会成为缺点,你能举例说明吗?
问题3: 在体育、文艺等各种比赛的评分中,使用的是平均数.计分过程中采用“去掉一个最高分,去掉一个最低分”的方法,说说这种方法的好处。
问题4:书本73页的探究如何理解?
问题5: 总结在利用众数、中位数、平均数估计总体的数字特征时各自的优缺点。
课中反思:
三种数字特征的优缺点
特征数 优 点 缺 点
众数 容易计算,体现了样本数据的最大集中点 无法客观反映总体特征,只能表示样本数据中的很少一部分信息,不一定唯一。
中位数 不受少数极端值的影响 中位数仅利用了数据中排在中间数据的信息,与数据的排列位置有关
平均数 与每一个数据有关,更能反映全体的信息 受每个样本数据的影响,使其在估计总体时的可靠性降低.
[例] 某中学举行电脑知识竞赛,现将高一参赛学生的成绩进行整理后分成五组绘制成如图所示的频率分布直方图,
求:高一参赛学生的成绩的众数、中位数及平均成绩.
典例解析
1.数据:1,1,3,3的众数和中位数分别是 ( )
A.1和3,2 B.3,2
C.1和3,1和3 D.3,3
2.频率分布直方图中最高小矩形的中间位置所对的数字特征是( )
A.中位数 B.众数
C.平均数 D.标准差
当堂训练
90
100
110
120
130
140
150
次数
0
0.004
0.008
0.012
0.01
0.020
0.024
0.028
频率/组距
0.032
0.036
3.为了了解高一学生的体能情况,某校抽取部分学生进行
一分钟跳绳次数次测试,将所得数据整理后,画出频率
分布直方图,图中从左到右各小长方形面积之比为
2:4:17:15:9:3,第二小组频数为12.
(1)第二小组的频率是多少?
样本容量是多少?
(2)在这次测试中,
学生跳绳次数的中位
数落在哪个小组内?
请说明理由
众数:最高矩形的中点的横坐标。
中位数:两边小长方形面积相等
平均数:频率分布直方图中每个小矩形的面积乘以小矩形底边中点的横坐标之和。
课堂小结
1、如何从样本数据中求众数、平均数、中位数的方法
2、如何从频率分布直方图中估计众数、中位数、平均数?
课本79页3题
习题2.2A组1,5,6,7
作业布置
谢谢大家
感谢各位领导和老师们的
指导,请多提宝贵意见!
