广东省中山市2021-2022 学年高三上学期期末统一考试数学试卷(Word版含答案)
文档属性
| 名称 | 广东省中山市2021-2022 学年高三上学期期末统一考试数学试卷(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-17 19:48:44 | ||
图片预览




文档简介
中山市2021-2022 学年高三上学期期末统一考试
数学试卷
本试卷满分150分。考试时间120分钟.
注意事项:
答卷前, 考生务必将自己的妵名、统考考号、座位号写在答题卡上.
每小题选出答案后, 用铅筁把答题卡上对应题目的答案标号涂黑, 如需改动, 用橡皮擦干净后, 再选涂其它荅案, 不能答在试题上.
不可以使用计算器.
考试结束, 将答题卡交回, 试卷不用上交.
第 I 卷 (选择题 共60分)
一、选择题: 本大题共 8 小题, 每小题 5 分, 共 40 分. 在每小题给出的四个选项中, 只有 一项是符合题目要求的.
设全集 与集合 的关系如图所示, 则图中阴影部分所表示的集合是()
A.
B.
C.
D.
已知向量 的夹角为 , , 则 ( )
A. 2
B.
C.
D. 12
已知 为正项等比数列, 且 , 设 为该数列的前 项积, 则 ( )
A. 8
B. 16
C. 32
D. 64
3 男 3 女六位同学站成一排, 则 3 位女生中有且只有两位女生相邻的不同排法种数是 ( )
A. 576
B. 432
C. 388
D. 216
抛物线 上一点 到其焦点的距离为 3 , 则抛物线 的方程为 ( )
A.
B.
C.
D.
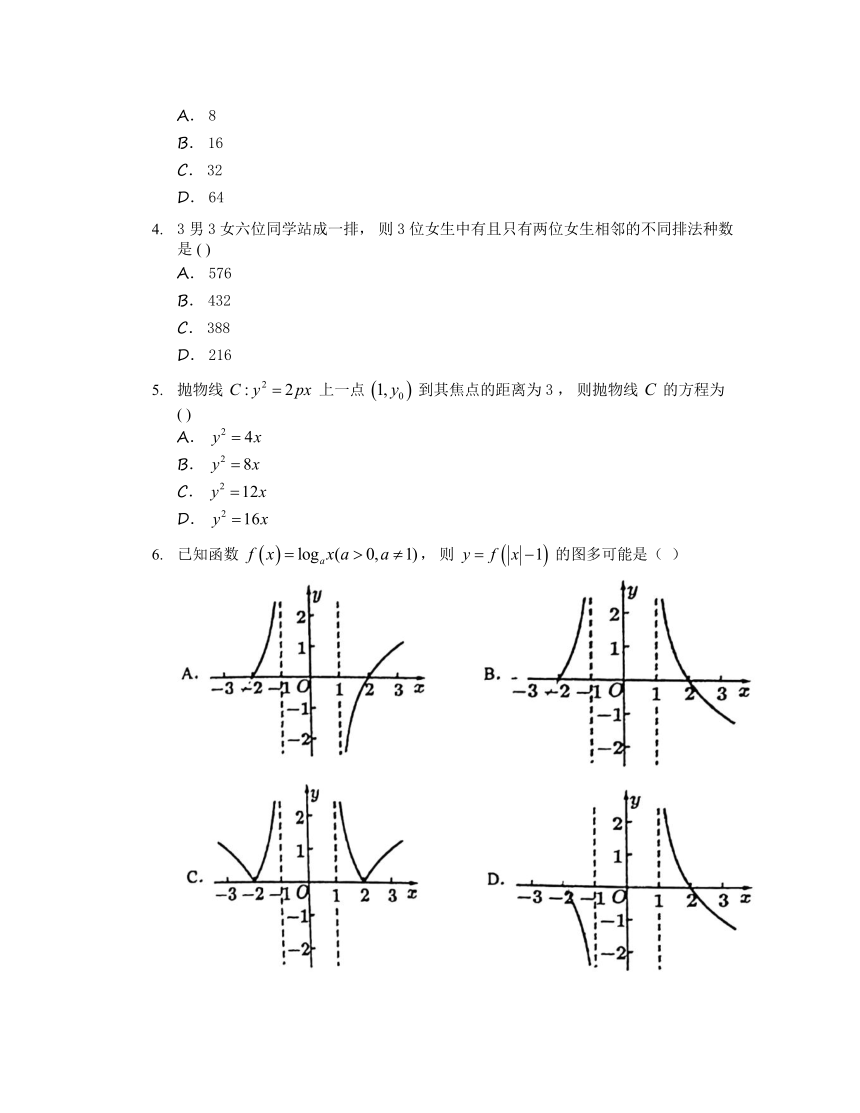
已知函数 , 则 的图多可能是( )
如图, 在棱长为 2 的正方体 中, 过 且与 平行的平面交 于点 ,则
A. 2
B.
C.
D. 1
甲、乙两支田径队的体检结果为:甲队队召体重的平均数为 , 方差为 200 ; 乙队员体重的平均数为 , 方差为 300 . 又已知甲、乙两队的队员人数之比为 , 么甲乙两队全部队员的平均体丘和方差分别是()
A. 65,280
B. 68,280
C. 65,296
D. 68,296
二、选择题:本大题共4小题,每小题5分.在每小题给出的选项中,有多项符合题目要
求.全部选对的得5分,部分选对的得2分,有选错的得0分.
已知函数 的部分图象如图所示, 下列说法正确 的是
A. 函数 的图象关于点 对称
B. 函数 的图象关于直线 对称
C. 函数 在 上单调递减
D. 函数 图象向右平移 个单位可得函数 的图象
已知 , 则下列选项中正确的是 ( )
A. 的最大值为 3
B. 的最大值为
C. 的最大值为
D. 的最小值为 2
已知函数 , 则下列说法正确的是 ( )
A. 函数 是偶函数
B. 函数 是奇函数
C. 函数 在 上单调递增
D. 函数 的值域为
已知球 的半径为 2 , 球心 在平面角大小为 的二面角 内, 二面角 的两个半平面分别截球面得两个圆 , 若两圆 的公共弦 的 长为 为 的中点, 四面体 的体积为 , 则下列结论中正确的有 ( )
A. 四点共面
B.
C.
D. 的最大值为
第Ⅱ卷(非选择题共90分 )
三、填空题: 本大题共 4 小题, 每小题 5 分, 共 20 分. 请将答案填在答题卡对应题号的位 置上. 答错位置, 书写不清, 模棱两可均不得分.
若 , 则 ________.
在数列 中, , 则数列的通项公式 ________.
已知复数 满足方程 , 则 ________.
已知点 为双曲线 在第一象限上一点, 点 为双曲线 的右焦点, 为坐标原点, 且 , 则双曲线 的离心率为________ ; 若直线 分别交双曲线 于 两点, 记直线 与 的 斜率分别为 , 则 ________. (本题第一空 2 分, 第二空 3 分)
四、解答题: 本大题共 6 个小题, 共 70 分. 解答应写出文字说明、证明过程或演算步骤.
(本小题满分 10 分)
已知数列 满足 , 且数列 是等差数列.
(1) 求数列 的通项公式:
(2) 设数列 的前 项和为 , 若 且 , 求集合 中所有元素的和 .
(本小题满分 12 分)
如图, 已知圆锥 的底面半径为 2 , 母线长为 , 点 为圆锥底面圆周上的一点, 为圆心, 是 的中点, 且 .
(1) 求三棱锥 的表面积;
(2) 求 到平面 的距离.
(本小题满分 12 分)
在 中,内角 的对边分别为 , 且 .
(1) 求 ;
(2) 已知 为 的中点, 点 在 上, 且满足 , 求 的面积.
(本小题满分 12 分)
某科技公司组织技术人员迩行某新项目研发,技术人员将独立地进行项目中不同类型的实验甲、乙、丙, 已知实验甲、乙、丙成功的概率分别为 .
(1)对实验甲、乙、丙各进行一次, 求至少有一次成功的概率;
(2)该项目研发流程如下: 实验甲做一次,若成功,则奖励技术人员 1 万元并进行实验乙, 否则技术人员不获得奖励且该项目终止; 实验乙做两次,若两次都成功, 则追加技术人员 3 万元奖励并进行实验丙, 否则技术人员不追加奖励且该项目终止; 实验丙做三次, 若至少两次成功, 则项目研发成功, 再追加技术人员 4 万元奖励, 否则不追加奖励且该项目终止.每次实验相互独立, 用 (单似: 万元) 表示技术人员所获得奖励的数值, 写出 的分布列及数学期望.
(本小题满分 12 分)
已知椭圆 的右你点为 , 离心率为 , 直线被椭圆截得的弦长为 .
(1) 求椭圆 的标倠方程
(2) 若P足椭圆C上一点,O是坐标原点, 过点F与直线l平行的直线与椭圆C的两个交点为 , 且 , 求 的最大值.
(本小题满分 12 分)
已知函数 .
(1)当 时, 求函数 的单调区间;
(2) 讨论 的零点个数.
数学试卷
本试卷满分150分。考试时间120分钟.
注意事项:
答卷前, 考生务必将自己的妵名、统考考号、座位号写在答题卡上.
每小题选出答案后, 用铅筁把答题卡上对应题目的答案标号涂黑, 如需改动, 用橡皮擦干净后, 再选涂其它荅案, 不能答在试题上.
不可以使用计算器.
考试结束, 将答题卡交回, 试卷不用上交.
第 I 卷 (选择题 共60分)
一、选择题: 本大题共 8 小题, 每小题 5 分, 共 40 分. 在每小题给出的四个选项中, 只有 一项是符合题目要求的.
设全集 与集合 的关系如图所示, 则图中阴影部分所表示的集合是()
A.
B.
C.
D.
已知向量 的夹角为 , , 则 ( )
A. 2
B.
C.
D. 12
已知 为正项等比数列, 且 , 设 为该数列的前 项积, 则 ( )
A. 8
B. 16
C. 32
D. 64
3 男 3 女六位同学站成一排, 则 3 位女生中有且只有两位女生相邻的不同排法种数是 ( )
A. 576
B. 432
C. 388
D. 216
抛物线 上一点 到其焦点的距离为 3 , 则抛物线 的方程为 ( )
A.
B.
C.
D.
已知函数 , 则 的图多可能是( )
如图, 在棱长为 2 的正方体 中, 过 且与 平行的平面交 于点 ,则
A. 2
B.
C.
D. 1
甲、乙两支田径队的体检结果为:甲队队召体重的平均数为 , 方差为 200 ; 乙队员体重的平均数为 , 方差为 300 . 又已知甲、乙两队的队员人数之比为 , 么甲乙两队全部队员的平均体丘和方差分别是()
A. 65,280
B. 68,280
C. 65,296
D. 68,296
二、选择题:本大题共4小题,每小题5分.在每小题给出的选项中,有多项符合题目要
求.全部选对的得5分,部分选对的得2分,有选错的得0分.
已知函数 的部分图象如图所示, 下列说法正确 的是
A. 函数 的图象关于点 对称
B. 函数 的图象关于直线 对称
C. 函数 在 上单调递减
D. 函数 图象向右平移 个单位可得函数 的图象
已知 , 则下列选项中正确的是 ( )
A. 的最大值为 3
B. 的最大值为
C. 的最大值为
D. 的最小值为 2
已知函数 , 则下列说法正确的是 ( )
A. 函数 是偶函数
B. 函数 是奇函数
C. 函数 在 上单调递增
D. 函数 的值域为
已知球 的半径为 2 , 球心 在平面角大小为 的二面角 内, 二面角 的两个半平面分别截球面得两个圆 , 若两圆 的公共弦 的 长为 为 的中点, 四面体 的体积为 , 则下列结论中正确的有 ( )
A. 四点共面
B.
C.
D. 的最大值为
第Ⅱ卷(非选择题共90分 )
三、填空题: 本大题共 4 小题, 每小题 5 分, 共 20 分. 请将答案填在答题卡对应题号的位 置上. 答错位置, 书写不清, 模棱两可均不得分.
若 , 则 ________.
在数列 中, , 则数列的通项公式 ________.
已知复数 满足方程 , 则 ________.
已知点 为双曲线 在第一象限上一点, 点 为双曲线 的右焦点, 为坐标原点, 且 , 则双曲线 的离心率为________ ; 若直线 分别交双曲线 于 两点, 记直线 与 的 斜率分别为 , 则 ________. (本题第一空 2 分, 第二空 3 分)
四、解答题: 本大题共 6 个小题, 共 70 分. 解答应写出文字说明、证明过程或演算步骤.
(本小题满分 10 分)
已知数列 满足 , 且数列 是等差数列.
(1) 求数列 的通项公式:
(2) 设数列 的前 项和为 , 若 且 , 求集合 中所有元素的和 .
(本小题满分 12 分)
如图, 已知圆锥 的底面半径为 2 , 母线长为 , 点 为圆锥底面圆周上的一点, 为圆心, 是 的中点, 且 .
(1) 求三棱锥 的表面积;
(2) 求 到平面 的距离.
(本小题满分 12 分)
在 中,内角 的对边分别为 , 且 .
(1) 求 ;
(2) 已知 为 的中点, 点 在 上, 且满足 , 求 的面积.
(本小题满分 12 分)
某科技公司组织技术人员迩行某新项目研发,技术人员将独立地进行项目中不同类型的实验甲、乙、丙, 已知实验甲、乙、丙成功的概率分别为 .
(1)对实验甲、乙、丙各进行一次, 求至少有一次成功的概率;
(2)该项目研发流程如下: 实验甲做一次,若成功,则奖励技术人员 1 万元并进行实验乙, 否则技术人员不获得奖励且该项目终止; 实验乙做两次,若两次都成功, 则追加技术人员 3 万元奖励并进行实验丙, 否则技术人员不追加奖励且该项目终止; 实验丙做三次, 若至少两次成功, 则项目研发成功, 再追加技术人员 4 万元奖励, 否则不追加奖励且该项目终止.每次实验相互独立, 用 (单似: 万元) 表示技术人员所获得奖励的数值, 写出 的分布列及数学期望.
(本小题满分 12 分)
已知椭圆 的右你点为 , 离心率为 , 直线被椭圆截得的弦长为 .
(1) 求椭圆 的标倠方程
(2) 若P足椭圆C上一点,O是坐标原点, 过点F与直线l平行的直线与椭圆C的两个交点为 , 且 , 求 的最大值.
(本小题满分 12 分)
已知函数 .
(1)当 时, 求函数 的单调区间;
(2) 讨论 的零点个数.
同课章节目录
