安徽省桐城市第二中学2021-2022学年九年级上学期期末考试数学试题(word版含答案)
文档属性
| 名称 | 安徽省桐城市第二中学2021-2022学年九年级上学期期末考试数学试题(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 203.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-17 00:00:00 | ||
图片预览



文档简介
桐城二中2021-2022学年度第一学期期末学情调研考试
九年级数学
考试时间:120分钟 满分:150分
一、选择题(本大题共10小题,共40.0分)
下列几何图形中,既是轴对称图形又是中心对称图形的是
等腰三角形 B. 平行四边形 C. 矩形 D. 正五边形
已知函数的图象在其所在的每个象限内随的增大而增大,则的值可能为
A. B. C. D.
平面直角坐标系中,抛物线经变换后得到抛物线,则这个变换是
A. 向左平移个单位 B. 向右平移个单位
C. 向左平移个单位 D. 向右平移个单位
如图,在平面直角坐标系中,点坐标为,则的值为
A. B. C. D.
第4题图 第5题图
如图,在中,,,,则线段的长度是
B. C. D.
已知圆锥的母线长为,侧面积为,则圆锥的底面半径为
A. B. C. D.
如图,在中,平分交于点过点作交于点,若::,且的面积为,则的面积为
A. B. C. D.
第7题图 第8题图
如图,是的外接圆,,,于点,且,则的半径为
A. B. C. D.
如图,中,,,与轴相交于点,平分,点在双曲线上,点在双曲线上,则的值为
A.
B.
C.
D.
已知中,点为边上一点,则下列四个说法中,一定正确的有
连接,若为中点,且平分,则;
若,且,则;
若,且,则;
若,,且平分,则的重心在上.
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共4小题,共20.0分)
已知若则的值为______.
已知二次函数的图象上有两点,,则,的大小关系为______.
第13题图 第14题图
往水平放置的半径为的圆柱形容器内装入一些水以后,截面图如图所示,若水面宽度,求水面深度的最大值______.
如图,在中,,是它的内角平分线,点是上的动点,已知,,则:
______.
的最小值是______.
三、解答题(本大题共9小题,15-18每题8分,19-20每题10分,21-22每题12分,23题14分,共90.0分)
计算:.
二次函数的图象与轴交于、两点,与轴交点,点坐标为,点坐标为,且的面积为.
求点的坐标;求该二次函数的表达式。
17.如图,在由边长为1个单位长度的小正方形组成的10×10网格中,线段AB的端点A、B均为网格线的交点。
(1)将线段AB先向上平移4个单位长度,再向右平移3个单位长度得到线段A1B1,画出线段A1B1;
(2)将线段绕点A1顺时针旋转90°得到线段A2B2,画出线段A1B2;
(3)连接BB1,直接写出sin∠B1BA= .
18.汽车盲区是指驾驶员位于驾驶座位置,其视线被车体遮挡而不能直接观察到的区域.如图,、分别为汽车两侧盲区的示意图,已知视线与地面的夹角,视线与地面的夹角,点,分别为,与车窗底部的交点,,,垂直于地面,点到点的距离米(参考数据:,,
求盲区中的长度;
点在上,MD=1.8米,在处有一个高度为的物体,驾驶员能观察到物体吗?请说明理由.
19.如图,一次函数的图象与反比例函数在第一象限的图象交于和两点,与轴交于点.
求反比例函数的解析式;
求出另一个交点的坐标,并直接写出当时,不等式
的解集;
若点在轴上,且的面积为,求点的坐标.
20.已知在中,,以为直径的分别交于,交于,连接.
求证:;
若,,求的长.
21.已知如图,,点在射线上,,点在射线上.
给出条件:;;能使的长唯一确定的条件是______填序号;
在第题中选一个使的长唯一确定的条件,求出此时的长度.
22.女生排球考试要求:垫球后,球在运动中离地面的最大高度至少为米.某次模拟测试中,某女生在处将球垫偏,之后又在,两处先后垫球,球沿抛物线运动假设抛物线,,在同一平面内,最终正好在处垫住,处离地面的距离为米.如图所示,以为坐标原点,米为单位长度建立直角坐标系,轴平行于地面水平直线,已知点,点的横坐标为,抛物线和的表达式分别为和.
求抛物线的函数表达式;
第一次垫球后,球在运动中离地面的最大高度是否达到要求?请说明理由;
为了使第三次垫球后,球在运动中离地面的最大高度达到要求,该女生第三次垫球处离地面的高度至少为多少米?
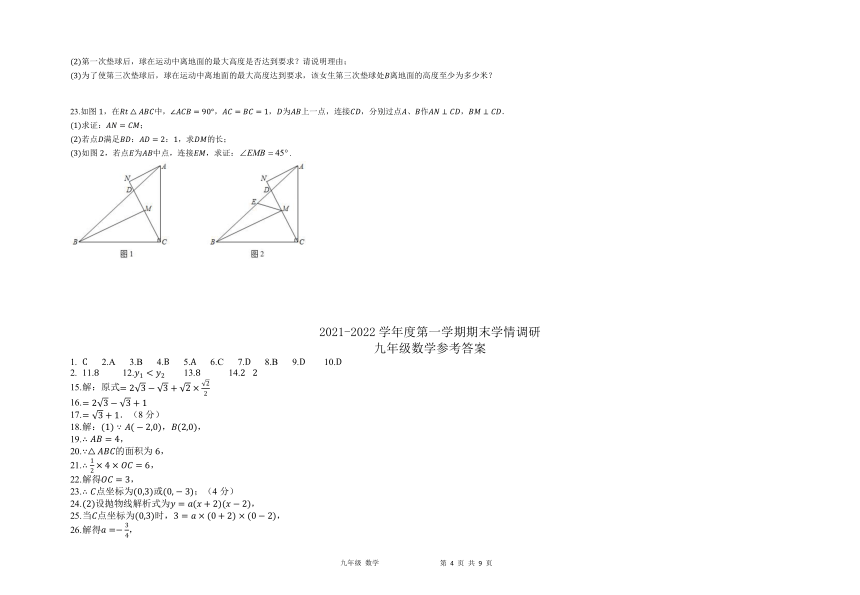
23.如图,在中,,,为上一点,连接,分别过点、作,.
求证:;
若点满足::,求的长;
如图,若点为中点,连接,求证:.
2021-2022学年度第一学期期末学情调研
九年级数学参考答案
2.A 3.B 4. 5. 6.C 7. 8.B 9. 10.
11. 12. 13. 14.
解:原式
.(8分)
解:,,
,
的面积为,
,
解得,
点坐标为或;(4分)
设抛物线解析式为,
当点坐标为时,,
解得,
此时抛物线解析式为,即;
当点坐标为时,,
解得,
此时抛物线解析式为,即;
综上所述,抛物线解析式为或.(8分)
、(1)如图;(2)如图(3);(8分)
解:,,,
,
在中,,,,
,
,
在中,,
,
,
答:盲区中的长度为;(4分)
驾驶员能观察到物体,理由如下:
如图所示:过点作,交于,则,
,,
,在中,
,
在处有一个高度为的物体,驾驶员能观察到物体.(8分)
19解:把点代入,得,
把代入反比例函数,
;
反比例函数的表达式为;(2分)
解得或,
,
由图象可知,当时,不等式的解集或;(4分)
在直线中,令,则,
,
设,
,
的面积为,
,
,
或,
或.(4分)
20.证明:、,
,
又,
,
,
;(5分)
解:连接,
是直径,
,
又,
,
、,
∽,
::,
又,,,
.(5分)
21.解:条件能使得唯一确定;
故答案为:;(4分)
当时,如图中,过点作于点.
,
,
,,
,
,
,
或当时,如图中,过点作于点.
,
,
.(12分)
22.解::,
将代入,得:,
解得:,
:;(3分)
由得:,
的对称轴为直线,顶点为,
处距离地面米,
最大高度为,
未达到要求;(7分)
(3)
高度至少应为米.
该女生第三次垫球处离地面至少为1.75米。(12分)
23.证明:,,
,,
又,
,
,
又,
≌,
;(4分)
解:,,
∽,
,
设,则,
由知,,
,
,
,
,,
,
;(9分)
解:延长,相交于点,
为的中点,
,
,,
,
,,
≌,
,
又,,
,
,
,,(14分)
九年级 数学
九年级数学
考试时间:120分钟 满分:150分
一、选择题(本大题共10小题,共40.0分)
下列几何图形中,既是轴对称图形又是中心对称图形的是
等腰三角形 B. 平行四边形 C. 矩形 D. 正五边形
已知函数的图象在其所在的每个象限内随的增大而增大,则的值可能为
A. B. C. D.
平面直角坐标系中,抛物线经变换后得到抛物线,则这个变换是
A. 向左平移个单位 B. 向右平移个单位
C. 向左平移个单位 D. 向右平移个单位
如图,在平面直角坐标系中,点坐标为,则的值为
A. B. C. D.
第4题图 第5题图
如图,在中,,,,则线段的长度是
B. C. D.
已知圆锥的母线长为,侧面积为,则圆锥的底面半径为
A. B. C. D.
如图,在中,平分交于点过点作交于点,若::,且的面积为,则的面积为
A. B. C. D.
第7题图 第8题图
如图,是的外接圆,,,于点,且,则的半径为
A. B. C. D.
如图,中,,,与轴相交于点,平分,点在双曲线上,点在双曲线上,则的值为
A.
B.
C.
D.
已知中,点为边上一点,则下列四个说法中,一定正确的有
连接,若为中点,且平分,则;
若,且,则;
若,且,则;
若,,且平分,则的重心在上.
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共4小题,共20.0分)
已知若则的值为______.
已知二次函数的图象上有两点,,则,的大小关系为______.
第13题图 第14题图
往水平放置的半径为的圆柱形容器内装入一些水以后,截面图如图所示,若水面宽度,求水面深度的最大值______.
如图,在中,,是它的内角平分线,点是上的动点,已知,,则:
______.
的最小值是______.
三、解答题(本大题共9小题,15-18每题8分,19-20每题10分,21-22每题12分,23题14分,共90.0分)
计算:.
二次函数的图象与轴交于、两点,与轴交点,点坐标为,点坐标为,且的面积为.
求点的坐标;求该二次函数的表达式。
17.如图,在由边长为1个单位长度的小正方形组成的10×10网格中,线段AB的端点A、B均为网格线的交点。
(1)将线段AB先向上平移4个单位长度,再向右平移3个单位长度得到线段A1B1,画出线段A1B1;
(2)将线段绕点A1顺时针旋转90°得到线段A2B2,画出线段A1B2;
(3)连接BB1,直接写出sin∠B1BA= .
18.汽车盲区是指驾驶员位于驾驶座位置,其视线被车体遮挡而不能直接观察到的区域.如图,、分别为汽车两侧盲区的示意图,已知视线与地面的夹角,视线与地面的夹角,点,分别为,与车窗底部的交点,,,垂直于地面,点到点的距离米(参考数据:,,
求盲区中的长度;
点在上,MD=1.8米,在处有一个高度为的物体,驾驶员能观察到物体吗?请说明理由.
19.如图,一次函数的图象与反比例函数在第一象限的图象交于和两点,与轴交于点.
求反比例函数的解析式;
求出另一个交点的坐标,并直接写出当时,不等式
的解集;
若点在轴上,且的面积为,求点的坐标.
20.已知在中,,以为直径的分别交于,交于,连接.
求证:;
若,,求的长.
21.已知如图,,点在射线上,,点在射线上.
给出条件:;;能使的长唯一确定的条件是______填序号;
在第题中选一个使的长唯一确定的条件,求出此时的长度.
22.女生排球考试要求:垫球后,球在运动中离地面的最大高度至少为米.某次模拟测试中,某女生在处将球垫偏,之后又在,两处先后垫球,球沿抛物线运动假设抛物线,,在同一平面内,最终正好在处垫住,处离地面的距离为米.如图所示,以为坐标原点,米为单位长度建立直角坐标系,轴平行于地面水平直线,已知点,点的横坐标为,抛物线和的表达式分别为和.
求抛物线的函数表达式;
第一次垫球后,球在运动中离地面的最大高度是否达到要求?请说明理由;
为了使第三次垫球后,球在运动中离地面的最大高度达到要求,该女生第三次垫球处离地面的高度至少为多少米?
23.如图,在中,,,为上一点,连接,分别过点、作,.
求证:;
若点满足::,求的长;
如图,若点为中点,连接,求证:.
2021-2022学年度第一学期期末学情调研
九年级数学参考答案
2.A 3.B 4. 5. 6.C 7. 8.B 9. 10.
11. 12. 13. 14.
解:原式
.(8分)
解:,,
,
的面积为,
,
解得,
点坐标为或;(4分)
设抛物线解析式为,
当点坐标为时,,
解得,
此时抛物线解析式为,即;
当点坐标为时,,
解得,
此时抛物线解析式为,即;
综上所述,抛物线解析式为或.(8分)
、(1)如图;(2)如图(3);(8分)
解:,,,
,
在中,,,,
,
,
在中,,
,
,
答:盲区中的长度为;(4分)
驾驶员能观察到物体,理由如下:
如图所示:过点作,交于,则,
,,
,在中,
,
在处有一个高度为的物体,驾驶员能观察到物体.(8分)
19解:把点代入,得,
把代入反比例函数,
;
反比例函数的表达式为;(2分)
解得或,
,
由图象可知,当时,不等式的解集或;(4分)
在直线中,令,则,
,
设,
,
的面积为,
,
,
或,
或.(4分)
20.证明:、,
,
又,
,
,
;(5分)
解:连接,
是直径,
,
又,
,
、,
∽,
::,
又,,,
.(5分)
21.解:条件能使得唯一确定;
故答案为:;(4分)
当时,如图中,过点作于点.
,
,
,,
,
,
,
或当时,如图中,过点作于点.
,
,
.(12分)
22.解::,
将代入,得:,
解得:,
:;(3分)
由得:,
的对称轴为直线,顶点为,
处距离地面米,
最大高度为,
未达到要求;(7分)
(3)
高度至少应为米.
该女生第三次垫球处离地面至少为1.75米。(12分)
23.证明:,,
,,
又,
,
,
又,
≌,
;(4分)
解:,,
∽,
,
设,则,
由知,,
,
,
,
,,
,
;(9分)
解:延长,相交于点,
为的中点,
,
,,
,
,,
≌,
,
又,,
,
,
,,(14分)
九年级 数学
同课章节目录
