【高考精粹】高考物理二轮夺分学案 专题04 电学中的曲线运动(有解析)
文档属性
| 名称 | 【高考精粹】高考物理二轮夺分学案 专题04 电学中的曲线运动(有解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-01-18 09:50:43 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
【高考精粹】高考物理二轮夺分学案
专题04 电学中的曲线运动
考纲要求 考频 考情分析
物质的电结构、电荷守恒 Ⅰ 1.命题趋势 分析历年命题情况可以发现命题有两大趋势: (1)本章内容在高考中单独命题较多,有选择题也有计算题. (2)常与实际生活、科学研究密切联系,通过新的情景或新的素材如喷墨打印机、静电除尘、示波管、加速器等进行命题考查. 2.备考策略 (1)关注库仑定律、电场线及其性质、电场强度、电势能和电势高低的判断、电容器等知识. (2)加强本章知识与物体间作用力、运动学、牛顿运动定律、功能关系等其他知识结合的计算题的训练.
静电现象的解释 Ⅰ
点电荷 Ⅰ
库仑定律 Ⅱ
静电场 Ⅰ
电场强度、点电荷的场强 Ⅱ 五年4考
电场线 Ⅰ 五年8考
电势能、电势 Ⅰ
电势差 Ⅱ
匀强电场中电势差与电场强度的关系 Ⅱ 五年1考
带电粒子在匀强电场中的运动 Ⅱ 五年6考
示波管 Ⅰ 五年3考
常见电容器、电容器的电压、电荷量和电容的关系 Ⅰ
带电粒子在电场中的偏转问题
考点剖析考点01
带电粒子在电场中的偏转问题
1.带电粒子在电场中的偏转规律
2.两个结论
(1)不同的带电粒子从静止开始经过同一电场加速后再从同一偏转电场射出时的偏转角度总是相同的.
证明:由qU0=mv02及tan φ=得tan φ=.
(2)粒子经电场偏转后,合速度的反向延长线与初速度延长线的交点O为粒子水平位移的中点,即O到电场边缘的距离为.
典型例题考点01
如图所示,真空中水平放置的两个相同极板Y和Y′长为L,相距d,足够大的竖直屏与两板右侧相距b,一束质量为m、带电荷量为+q的粒子(不计重力)从两板左侧中点A以初速度v0沿水平方向射入电场且能穿出.
(1)求粒子从射入到打到屏上所用的时间;
(2)证明粒子飞出电场后的速度方向的反向延长线交于两板间的中心O点.
[解析] (1)根据题意,粒子在垂直于电场线的方向上做匀速直线运动,所以粒子从射入到打到屏上所用的时间t=.
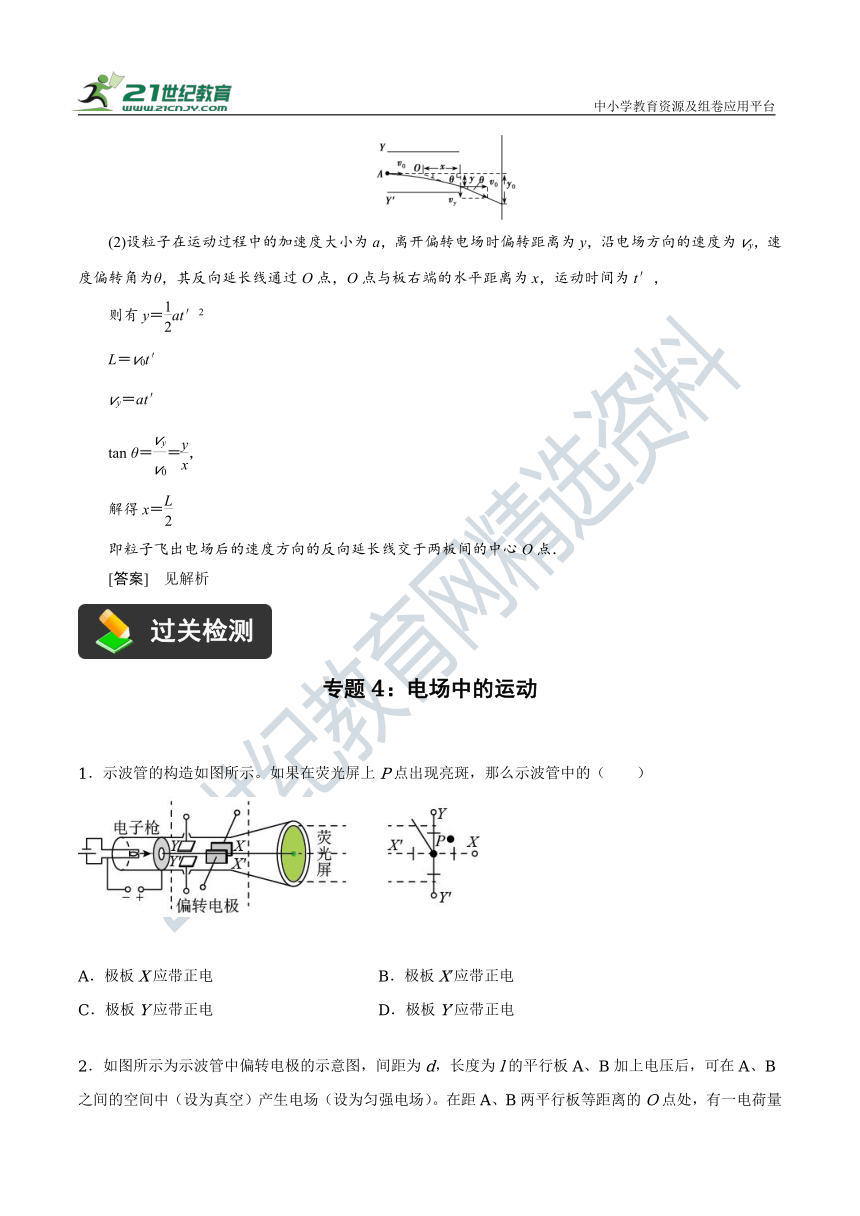
(2)设粒子在运动过程中的加速度大小为a,离开偏转电场时偏转距离为y,沿电场方向的速度为vy,速度偏转角为θ,其反向延长线通过O点,O点与板右端的水平距离为x,运动时间为t′,
则有y=at′2
L=v0t′
vy=at′
tan θ==,
解得x=
即粒子飞出电场后的速度方向的反向延长线交于两板间的中心O点.
[答案] 见解析
专题4:电场中的运动
1.示波管的构造如图所示。如果在荧光屏上P点出现亮斑,那么示波管中的( )
A.极板X应带正电 B.极板X′应带正电
C.极板Y应带正电 D.极板Y′应带正电
2.如图所示为示波管中偏转电极的示意图,间距为d,长度为l的平行板A、B加上电压后,可在A、B之间的空间中(设为真空)产生电场(设为匀强电场)。在距A、B两平行板等距离的O点处,有一电荷量为+q、质量为m的粒子以初速度v0沿水平方向(与A、B板平行)射入,不计重力,要使此粒子能从C处射出,则A、B间的电压应为( )
A. B. C. D.
3.如图所示,带电量之比为的带电粒子A、B,先后以相同的速度从同一点射入平行板电容器中,不计重力,带电粒子偏转后打在同一极板上,水平飞行距离之比为,则带电粒子的质量之比以及在电场中飞行时间之比分别为( )
A.1:1, 2:3
B.2:1, 3:2
C.1:1 ,3:4
D.4:3, 2:1
4.如图甲,某装置由多个横截面积相同的金属圆筒依次排列,其中心轴线在同一直线上,圆筒的长度依照一定的规律依次增加。序号为奇数的圆筒和交变电源的一个极相连,序号为偶数的圆筒和该电源的另一个极相连。
交变电源两极间电势差的变化规律如图乙所示。在时,奇数圆筒相对偶数圆筒的电势差为正值,此时位于和偶数圆筒相连的金属圆板(序号为0)中央的一个电子,在圆板和圆筒1之间的电场中由静止开始加速,沿中心轴线冲进圆筒1。
为使电子运动到圆筒与圆筒之间各个间隙中都能恰好使静电力的方向跟运动方向相同而不断加速,圆筒长度的设计必须遵照一定的规律。若已知电子的质量为、电子电荷量为、电压的绝对值为,周期为,电子通过圆筒间隙的时间可以忽略不计。则金属圆筒的长度和它的序号之间有什么定量关系?第个金属圆筒的长度应该是多少?
5.如图,两相同极板与的长度为,相距为,极板间的电压为。一个电子沿平行于板面的方向射入电场中,射入时的速度为。把两板间的电场看作匀强电场,求电子射出电场时沿垂直于板面方向偏移的距离和偏转的角度。
6.真空中有一对平行金属板,相距,两板电势差为。二价的氧离子由静止开始加速,从一个极板到达另一个极板时,动能是多大?这个问题有几种解法?哪种解法比较简便?
7.某种金属板受到一束紫外线照射时会不停地发射电子,射出的电子具有不同的方向,速度大小也不相同。在旁放置一个金属网。如果用导线将、连起来,从射出的电子落到上便会沿导线返回,从而形成电流。现在不把、直接相连,而按图那样在、之间加电压,发现当时电流表中就没有电流。
问:被这束紫外线照射出的电子,最大速度是多少?
8.先后让一束电子和一束氢核通过同一对平行板形成的偏转电场,进入时速度方向与电场方向垂直。在下列两种情况下,分别求出电子偏转角的正切与氢核偏转角的正切之比。
(1)电子与氢核的初速度相同。
(2)电子与氢核的初动能相同。
9.让一价氢离子、一价氦离子和二价氦离子的混合物由静止开始经过同一加速电场加速,然后在同一偏转电场里偏转,它们是否会分离为三股粒子束?请通过计算说明。
10.电子从静止出发被1000V的电压加速,然后进入另一个电场强度为5000N/C的匀强偏转电场,进入方向与电场强度方向垂直,已知偏转电极长6cm。求电子离开偏转电场时的速度及其与进入偏转电场时的速度方向之间的夹角。
11.某些肿瘤可以用“质子疗法”进行治疗。在这种疗法中,质子先被加速到具有较高的能量,然后被引向轰击肿瘤,杀死其中的恶性细胞,如图所示。若质子的加速长度为,要使质子由静止被加速到,加速匀强电场的电场强度应是多少?
12.一束电子流经的加速电压加速后,在距两极板等距离处垂直进入平行板间的匀强电场,如图所示,两极板间电压,两极板间距,板长。
(1)求电子在两极板间穿过时的偏移量y;
(2)若平行板的右边缘与屏的距离,求电子打在屏上的位置与中心O的距离Y(O点位于平行板水平中线的延长线上);
(3)若另一个质量为m(不计重力)的二价负离子经同一电压加速,再经同一偏转电场,射出偏转电场的偏移量和打在屏上的偏移量各是多大?
13.如图所示,电子从静止开始被U=180V的电场加速,沿直线垂直进入另一个场强为E=6000V/m的匀强偏转电场,而后电子从右侧离开偏转电场.已知电子比荷为≈×1011C/kg,不计电子的重力,偏转极板长为L=6.0×10-2m.求:
(1)电子经过电压U加速后的速度vx的大小;
(2)电子在偏转电场中运动的加速度a的大小;
(3)电子离开偏转电场时的速度方向与进入该电场时的速度方向之间的夹角θ.
参考答案
1.AC
【详解】
根据亮斑的位置,竖直方向上,向上偏转,电子受力向上,因此Y极板带正电;水平方向上,向X板偏转,电子受力指向X板,因此X板带正电。
故选AC。
2.A
【详解】
带电粒子只受电场力作用,在平行板间做类平抛运动。设粒子由O到C的运动时间为t,则有
l=v0t
设A、B间的电压为U,则偏转电极间的匀强电场的场强
粒子所受电场力
根据牛顿第二定律得粒子沿电场方向的加速度
粒子在沿电场方向做匀加速直线运动,位移为。由匀加速直线运动的规律得
解得
U=
BCD错误,A正确。
故选A。
3.D
【详解】
两个带电粒子垂直射入电场中做为平抛运动,水平方向做匀速直线运动,竖直方向做初速度为零的匀加速直线运动,则水平方向有
相等,所以,则得:
竖直方向有:
因为E、y、v0相等,则得:
故选D。
4.圆筒长度跟圆筒序号的平方根成正比,第个圆筒的长度是。
【详解】
设电子进入第个圆筒后的速度为,根据动能定理有
得
第个圆筒的长度为
圆筒长度跟圆筒序号的平方根成正比,第个圆筒的长度是。
5.电子射出电场时沿垂直于板面方向偏移的距离是,偏转的角度是
【详解】
电子在电场中运动的加速度是
电子射出电场时,在垂直于板面方向偏移的距离为
其中为飞行时间。
由于电子在平行于板面的方向不受力,所以在这个方向做匀速直线运动,由可求得
联立以上各式解得
代入数值得
即电子射出时沿垂直于板面的方向偏离。
由于电子在平行于板面的方向不受力,它离开电场时,这个方向的分速度仍是,垂直于板面的分速度是
则离开电场时的偏转角度可由下式确定
代入数值解得
所以电子射出电场时沿垂直于板面方向偏移的距离是,偏转的角度是。
6.180eV;两种解法:动能定理和运动学公式;动能定理比较简单。
【详解】
解法根据动能定理,有
qU= EK
解得
Ek=qU=2e×90V=180eV
解法二根据牛顿第二定律,有
qE=ma①
根据运动学公式,有
电场强度
动能
联立①②③④解得
Ek=qU=2e×90v=180ev
答:从一个极板到达另一个极板时,动能是180eV;用动能定理较为简单.
7.
【详解】
加上电压后,会在电子运动区域产生阻碍电子射向N板的运动,当电流表中无电流通过时,说明即使垂直射向N板的电子都会在到达N板前减速到零,假设电子最大速度是v,由动能定理得
电子质量m=0.91×10-30kg,e取,U0=12.5V,代入数值解得
8.;
【详解】
粒子在偏转电场中做类平抛运动,由动力学知识可得:
水平方向
L=v0t
加速度
竖直分速度
vy=at
速度偏向角的正切
(1)如果电子和氢核的初速度相同,由上公式,可知偏转角的正切值与质量成反比,所以离开时电子偏角的正切和氢核偏角的正切之比为
(2)如果电子和氢核的初动能相同,由上公式,可知偏转角的正切值与电量成正比,所以离开时氦核偏角的正切和氢核偏角的正切之比为
9.见解析
【详解】
设任一正电荷的电量为q,加速电压为U1,偏转电压为U2,偏转电极的极板为L,板间距离为d,在加速电场中,根据动能定理得
qU1=
在偏转电场中,离子做类平抛运动,运动时间
偏转距离
联立以上各式得
设偏转角度为θ,则
由上可知y、θ与带电粒子的质量、电荷量无关,则一价氢离子、一价氦离子和二价氦离子在偏转电场轨迹重合,所以它们不会分成三股,而是会聚为一束射出。
【点睛】
本题一方面要熟记结论:同种带电粒子经同一加速电场加速,再经同一偏转电场偏转时轨迹重合,另一方面要能运用力学方法进行推导。
10.速度1.9×107m/s,角度8.53°
【详解】
电子从静止被加速电场加速,据动能定理得
电子进入偏转电场后做类平抛运动,则
联立解得电子离开偏转电场时的速度
电子离开偏转电场时的速度与进入偏转电场时的速度方向之间的夹角
11.1.3×105V/m。
【详解】
质子的质量m=1.67×10-27kg,电量e=1.6×10-19C,加速质子过程中,由动能定理可得
其中质子的加速长度x=4.0m,解得加速匀强电场的电场强度
12.(1);(2);(3),
【详解】
(1)设电子经加速电压U1加速后获得的速度大小为v0,由动能定理得
①
电子在偏转电场中的加速度大小为
②
设电子做类平抛运动的时间为t,根据运动学规律有
③
④
联立①②③④并代入数据解得
⑤
(2)由类平抛运动规律的推论和几何关系知
⑥
解得
⑦
(3)由⑤⑦式可知y和Y与带电粒子的质量m和电荷量q均无关,所以
⑧
⑨
13.(1)(2)(3)
【详解】
(1)根据动能定理得:
代入数据解得:
;
(2)根据牛顿第二定律得:
代入数据得:
;
(3)粒子在电场中的运动时间为:
离开电场时的竖直分速度为:
根据平行四边形定则知:
代入数据解得:
.
【高考精粹】高考物理二轮夺分学案
专题04 电学中的曲线运动
考纲要求 考频 考情分析
物质的电结构、电荷守恒 Ⅰ 1.命题趋势 分析历年命题情况可以发现命题有两大趋势: (1)本章内容在高考中单独命题较多,有选择题也有计算题. (2)常与实际生活、科学研究密切联系,通过新的情景或新的素材如喷墨打印机、静电除尘、示波管、加速器等进行命题考查. 2.备考策略 (1)关注库仑定律、电场线及其性质、电场强度、电势能和电势高低的判断、电容器等知识. (2)加强本章知识与物体间作用力、运动学、牛顿运动定律、功能关系等其他知识结合的计算题的训练.
静电现象的解释 Ⅰ
点电荷 Ⅰ
库仑定律 Ⅱ
静电场 Ⅰ
电场强度、点电荷的场强 Ⅱ 五年4考
电场线 Ⅰ 五年8考
电势能、电势 Ⅰ
电势差 Ⅱ
匀强电场中电势差与电场强度的关系 Ⅱ 五年1考
带电粒子在匀强电场中的运动 Ⅱ 五年6考
示波管 Ⅰ 五年3考
常见电容器、电容器的电压、电荷量和电容的关系 Ⅰ
带电粒子在电场中的偏转问题
考点剖析考点01
带电粒子在电场中的偏转问题
1.带电粒子在电场中的偏转规律
2.两个结论
(1)不同的带电粒子从静止开始经过同一电场加速后再从同一偏转电场射出时的偏转角度总是相同的.
证明:由qU0=mv02及tan φ=得tan φ=.
(2)粒子经电场偏转后,合速度的反向延长线与初速度延长线的交点O为粒子水平位移的中点,即O到电场边缘的距离为.
典型例题考点01
如图所示,真空中水平放置的两个相同极板Y和Y′长为L,相距d,足够大的竖直屏与两板右侧相距b,一束质量为m、带电荷量为+q的粒子(不计重力)从两板左侧中点A以初速度v0沿水平方向射入电场且能穿出.
(1)求粒子从射入到打到屏上所用的时间;
(2)证明粒子飞出电场后的速度方向的反向延长线交于两板间的中心O点.
[解析] (1)根据题意,粒子在垂直于电场线的方向上做匀速直线运动,所以粒子从射入到打到屏上所用的时间t=.
(2)设粒子在运动过程中的加速度大小为a,离开偏转电场时偏转距离为y,沿电场方向的速度为vy,速度偏转角为θ,其反向延长线通过O点,O点与板右端的水平距离为x,运动时间为t′,
则有y=at′2
L=v0t′
vy=at′
tan θ==,
解得x=
即粒子飞出电场后的速度方向的反向延长线交于两板间的中心O点.
[答案] 见解析
专题4:电场中的运动
1.示波管的构造如图所示。如果在荧光屏上P点出现亮斑,那么示波管中的( )
A.极板X应带正电 B.极板X′应带正电
C.极板Y应带正电 D.极板Y′应带正电
2.如图所示为示波管中偏转电极的示意图,间距为d,长度为l的平行板A、B加上电压后,可在A、B之间的空间中(设为真空)产生电场(设为匀强电场)。在距A、B两平行板等距离的O点处,有一电荷量为+q、质量为m的粒子以初速度v0沿水平方向(与A、B板平行)射入,不计重力,要使此粒子能从C处射出,则A、B间的电压应为( )
A. B. C. D.
3.如图所示,带电量之比为的带电粒子A、B,先后以相同的速度从同一点射入平行板电容器中,不计重力,带电粒子偏转后打在同一极板上,水平飞行距离之比为,则带电粒子的质量之比以及在电场中飞行时间之比分别为( )
A.1:1, 2:3
B.2:1, 3:2
C.1:1 ,3:4
D.4:3, 2:1
4.如图甲,某装置由多个横截面积相同的金属圆筒依次排列,其中心轴线在同一直线上,圆筒的长度依照一定的规律依次增加。序号为奇数的圆筒和交变电源的一个极相连,序号为偶数的圆筒和该电源的另一个极相连。
交变电源两极间电势差的变化规律如图乙所示。在时,奇数圆筒相对偶数圆筒的电势差为正值,此时位于和偶数圆筒相连的金属圆板(序号为0)中央的一个电子,在圆板和圆筒1之间的电场中由静止开始加速,沿中心轴线冲进圆筒1。
为使电子运动到圆筒与圆筒之间各个间隙中都能恰好使静电力的方向跟运动方向相同而不断加速,圆筒长度的设计必须遵照一定的规律。若已知电子的质量为、电子电荷量为、电压的绝对值为,周期为,电子通过圆筒间隙的时间可以忽略不计。则金属圆筒的长度和它的序号之间有什么定量关系?第个金属圆筒的长度应该是多少?
5.如图,两相同极板与的长度为,相距为,极板间的电压为。一个电子沿平行于板面的方向射入电场中,射入时的速度为。把两板间的电场看作匀强电场,求电子射出电场时沿垂直于板面方向偏移的距离和偏转的角度。
6.真空中有一对平行金属板,相距,两板电势差为。二价的氧离子由静止开始加速,从一个极板到达另一个极板时,动能是多大?这个问题有几种解法?哪种解法比较简便?
7.某种金属板受到一束紫外线照射时会不停地发射电子,射出的电子具有不同的方向,速度大小也不相同。在旁放置一个金属网。如果用导线将、连起来,从射出的电子落到上便会沿导线返回,从而形成电流。现在不把、直接相连,而按图那样在、之间加电压,发现当时电流表中就没有电流。
问:被这束紫外线照射出的电子,最大速度是多少?
8.先后让一束电子和一束氢核通过同一对平行板形成的偏转电场,进入时速度方向与电场方向垂直。在下列两种情况下,分别求出电子偏转角的正切与氢核偏转角的正切之比。
(1)电子与氢核的初速度相同。
(2)电子与氢核的初动能相同。
9.让一价氢离子、一价氦离子和二价氦离子的混合物由静止开始经过同一加速电场加速,然后在同一偏转电场里偏转,它们是否会分离为三股粒子束?请通过计算说明。
10.电子从静止出发被1000V的电压加速,然后进入另一个电场强度为5000N/C的匀强偏转电场,进入方向与电场强度方向垂直,已知偏转电极长6cm。求电子离开偏转电场时的速度及其与进入偏转电场时的速度方向之间的夹角。
11.某些肿瘤可以用“质子疗法”进行治疗。在这种疗法中,质子先被加速到具有较高的能量,然后被引向轰击肿瘤,杀死其中的恶性细胞,如图所示。若质子的加速长度为,要使质子由静止被加速到,加速匀强电场的电场强度应是多少?
12.一束电子流经的加速电压加速后,在距两极板等距离处垂直进入平行板间的匀强电场,如图所示,两极板间电压,两极板间距,板长。
(1)求电子在两极板间穿过时的偏移量y;
(2)若平行板的右边缘与屏的距离,求电子打在屏上的位置与中心O的距离Y(O点位于平行板水平中线的延长线上);
(3)若另一个质量为m(不计重力)的二价负离子经同一电压加速,再经同一偏转电场,射出偏转电场的偏移量和打在屏上的偏移量各是多大?
13.如图所示,电子从静止开始被U=180V的电场加速,沿直线垂直进入另一个场强为E=6000V/m的匀强偏转电场,而后电子从右侧离开偏转电场.已知电子比荷为≈×1011C/kg,不计电子的重力,偏转极板长为L=6.0×10-2m.求:
(1)电子经过电压U加速后的速度vx的大小;
(2)电子在偏转电场中运动的加速度a的大小;
(3)电子离开偏转电场时的速度方向与进入该电场时的速度方向之间的夹角θ.
参考答案
1.AC
【详解】
根据亮斑的位置,竖直方向上,向上偏转,电子受力向上,因此Y极板带正电;水平方向上,向X板偏转,电子受力指向X板,因此X板带正电。
故选AC。
2.A
【详解】
带电粒子只受电场力作用,在平行板间做类平抛运动。设粒子由O到C的运动时间为t,则有
l=v0t
设A、B间的电压为U,则偏转电极间的匀强电场的场强
粒子所受电场力
根据牛顿第二定律得粒子沿电场方向的加速度
粒子在沿电场方向做匀加速直线运动,位移为。由匀加速直线运动的规律得
解得
U=
BCD错误,A正确。
故选A。
3.D
【详解】
两个带电粒子垂直射入电场中做为平抛运动,水平方向做匀速直线运动,竖直方向做初速度为零的匀加速直线运动,则水平方向有
相等,所以,则得:
竖直方向有:
因为E、y、v0相等,则得:
故选D。
4.圆筒长度跟圆筒序号的平方根成正比,第个圆筒的长度是。
【详解】
设电子进入第个圆筒后的速度为,根据动能定理有
得
第个圆筒的长度为
圆筒长度跟圆筒序号的平方根成正比,第个圆筒的长度是。
5.电子射出电场时沿垂直于板面方向偏移的距离是,偏转的角度是
【详解】
电子在电场中运动的加速度是
电子射出电场时,在垂直于板面方向偏移的距离为
其中为飞行时间。
由于电子在平行于板面的方向不受力,所以在这个方向做匀速直线运动,由可求得
联立以上各式解得
代入数值得
即电子射出时沿垂直于板面的方向偏离。
由于电子在平行于板面的方向不受力,它离开电场时,这个方向的分速度仍是,垂直于板面的分速度是
则离开电场时的偏转角度可由下式确定
代入数值解得
所以电子射出电场时沿垂直于板面方向偏移的距离是,偏转的角度是。
6.180eV;两种解法:动能定理和运动学公式;动能定理比较简单。
【详解】
解法根据动能定理,有
qU= EK
解得
Ek=qU=2e×90V=180eV
解法二根据牛顿第二定律,有
qE=ma①
根据运动学公式,有
电场强度
动能
联立①②③④解得
Ek=qU=2e×90v=180ev
答:从一个极板到达另一个极板时,动能是180eV;用动能定理较为简单.
7.
【详解】
加上电压后,会在电子运动区域产生阻碍电子射向N板的运动,当电流表中无电流通过时,说明即使垂直射向N板的电子都会在到达N板前减速到零,假设电子最大速度是v,由动能定理得
电子质量m=0.91×10-30kg,e取,U0=12.5V,代入数值解得
8.;
【详解】
粒子在偏转电场中做类平抛运动,由动力学知识可得:
水平方向
L=v0t
加速度
竖直分速度
vy=at
速度偏向角的正切
(1)如果电子和氢核的初速度相同,由上公式,可知偏转角的正切值与质量成反比,所以离开时电子偏角的正切和氢核偏角的正切之比为
(2)如果电子和氢核的初动能相同,由上公式,可知偏转角的正切值与电量成正比,所以离开时氦核偏角的正切和氢核偏角的正切之比为
9.见解析
【详解】
设任一正电荷的电量为q,加速电压为U1,偏转电压为U2,偏转电极的极板为L,板间距离为d,在加速电场中,根据动能定理得
qU1=
在偏转电场中,离子做类平抛运动,运动时间
偏转距离
联立以上各式得
设偏转角度为θ,则
由上可知y、θ与带电粒子的质量、电荷量无关,则一价氢离子、一价氦离子和二价氦离子在偏转电场轨迹重合,所以它们不会分成三股,而是会聚为一束射出。
【点睛】
本题一方面要熟记结论:同种带电粒子经同一加速电场加速,再经同一偏转电场偏转时轨迹重合,另一方面要能运用力学方法进行推导。
10.速度1.9×107m/s,角度8.53°
【详解】
电子从静止被加速电场加速,据动能定理得
电子进入偏转电场后做类平抛运动,则
联立解得电子离开偏转电场时的速度
电子离开偏转电场时的速度与进入偏转电场时的速度方向之间的夹角
11.1.3×105V/m。
【详解】
质子的质量m=1.67×10-27kg,电量e=1.6×10-19C,加速质子过程中,由动能定理可得
其中质子的加速长度x=4.0m,解得加速匀强电场的电场强度
12.(1);(2);(3),
【详解】
(1)设电子经加速电压U1加速后获得的速度大小为v0,由动能定理得
①
电子在偏转电场中的加速度大小为
②
设电子做类平抛运动的时间为t,根据运动学规律有
③
④
联立①②③④并代入数据解得
⑤
(2)由类平抛运动规律的推论和几何关系知
⑥
解得
⑦
(3)由⑤⑦式可知y和Y与带电粒子的质量m和电荷量q均无关,所以
⑧
⑨
13.(1)(2)(3)
【详解】
(1)根据动能定理得:
代入数据解得:
;
(2)根据牛顿第二定律得:
代入数据得:
;
(3)粒子在电场中的运动时间为:
离开电场时的竖直分速度为:
根据平行四边形定则知:
代入数据解得:
.
同课章节目录
