2021-2022学年北师大版数学七年级下册第三章 变量间的关系单元检测(Word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版数学七年级下册第三章 变量间的关系单元检测(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 156.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-18 00:24:58 | ||
图片预览


文档简介
变量之间的关系
本章检测
满分:100分,限时:60分钟
一、选择题(每题3分,共30分)
1.在△ABC中,它的底边是a,底边上的高是h,则三角形面积S=ah,当a为定长时,在此函数关系式中( )
A.S,h是变量,,a是常量 B.S,h,a是变量,是常量
C.a,h是变量,,S是常量 D.S是变量,,a,h是常量
2.一列快车从甲地开往乙地,一列慢车从乙地开往甲地,两车同时出发,两车离乙地的路程s(千米)与行驶时间t(小时)的关系如图所示,则下列结论中错误的是( )
A.甲、乙两地的路程是400千米 B.慢车行驶速度为60千米/小时
C.相遇时快车行驶了150千米 D.快车出发后4小时到达乙地
3.A、B两地相距20千米,甲、乙两人都从A地去B地,图中和分别表示甲、乙两人所走路程(千米)与时刻(小时)之间的关系.下列说法:
①乙晚出发1小时;
②乙出发3小时后追上甲;
③甲的速度是4千米/小时;
④乙先到达B地.
其中正确的个数是( )
A.1 B.2 C.3 D.4
4.某商场自行车存放处每周的存车量为5000辆次,其中变速车存车费是每辆一次1元,普通车存车费为每辆一次0. 5元,若普通车存车量为辆次,存车的总收入为元,则与之间的关系式是( )
A. B.
C. D.
5.某科研小组在网上获取了声音在空气中传播的速度与空气温度关系的一些数据(如下表):
温度/℃ ﹣20 ﹣10 0 10 20 30
声速/m/s 318 324 330 336 342 348
下列说法错误的是( )
A.在这个变化中,自变量是温度,因变量是声速
B.温度越高,声速越快
C.当空气温度为20℃时,声音5s可以传播1740m
D.当温度每升高10℃,声速增加6m/s
6.如图所示的函数图象反映的过程是:小徐从家去菜地浇水,又去玉米地除草,然后回家.其中x表示时间,y表示小徐离他家的距离.读图可知菜地离小徐家的距离为( )
A.1.1千米 B.2千米 C.15千米 D.37千米
7.小亮家与姥姥家相距24 km,小亮8:00从家出发,骑自行车去姥姥家.妈妈8:30从家出发,乘车沿相同路线去姥姥家.在同一直角坐标系中,小亮和妈妈的行进路程s(km)与时间t(h)的函数图象如图所示.根据图象得出下列结论,其中错误的是( )
A.小亮骑自行车的平均速度是12 km/h
B.妈妈比小亮提前0.5 h到达姥姥家
C.妈妈在距家12 km处追上小亮
D.9:30妈妈追上小亮
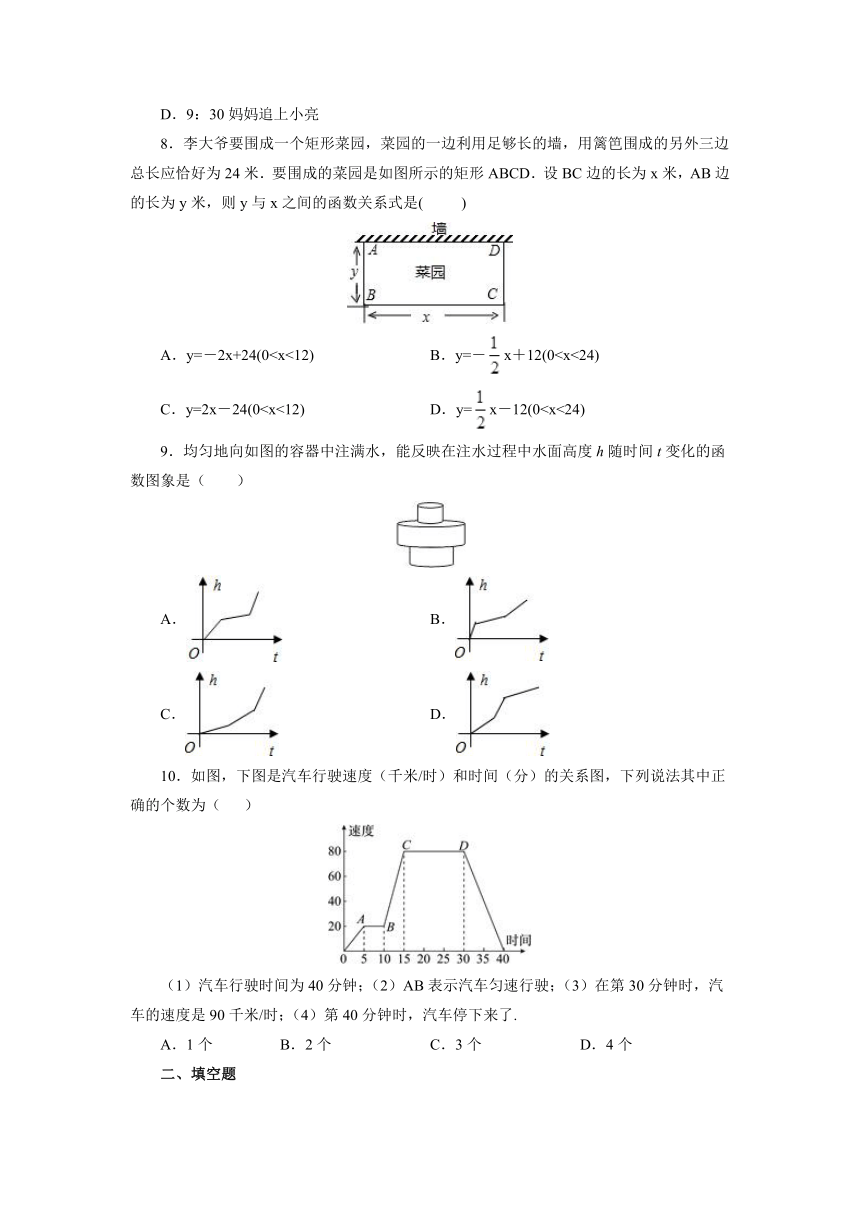
8.李大爷要围成一个矩形菜园,菜园的一边利用足够长的墙,用篱笆围成的另外三边总长应恰好为24米.要围成的菜园是如图所示的矩形ABCD.设BC边的长为x米,AB边的长为y米,则y与x之间的函数关系式是( )
A.y=-2x+24(0C.y=2x-24(09.均匀地向如图的容器中注满水,能反映在注水过程中水面高度h随时间t变化的函数图象是( )
A. B.
C. D.
10.如图,下图是汽车行驶速度(千米/时)和时间(分)的关系图,下列说法其中正确的个数为( )
(1)汽车行驶时间为40分钟;(2)AB表示汽车匀速行驶;(3)在第30分钟时,汽车的速度是90千米/时;(4)第40分钟时,汽车停下来了.
A.1个 B.2个 C.3个 D.4个
二、填空题
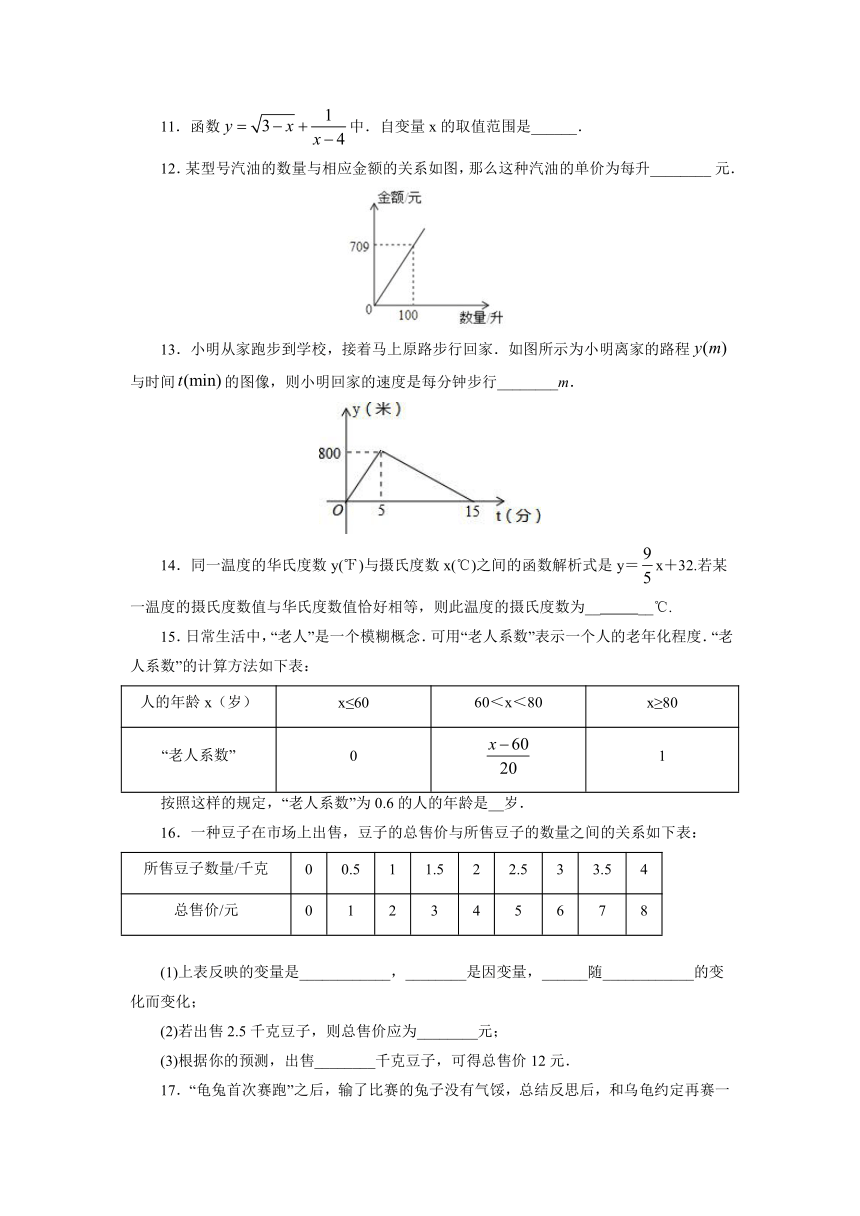
11.函数中.自变量x的取值范围是______.
12.某型号汽油的数量与相应金额的关系如图,那么这种汽油的单价为每升________ 元.
13.小明从家跑步到学校,接着马上原路步行回家.如图所示为小明离家的路程与时间的图像,则小明回家的速度是每分钟步行________m.
14.同一温度的华氏度数y(℉)与摄氏度数x(℃)之间的函数解析式是y=x+32.若某一温度的摄氏度数值与华氏度数值恰好相等,则此温度的摄氏度数为__ __℃.
15.日常生活中,“老人”是一个模糊概念.可用“老人系数”表示一个人的老年化程度.“老人系数”的计算方法如下表:
人的年龄x(岁) x≤60 60<x<80 x≥80
“老人系数” 0 1
按照这样的规定,“老人系数”为0.6的人的年龄是__岁.
16.一种豆子在市场上出售,豆子的总售价与所售豆子的数量之间的关系如下表:
所售豆子数量/千克 0 0.5 1 1.5 2 2.5 3 3.5 4
总售价/元 0 1 2 3 4 5 6 7 8
(1)上表反映的变量是____________,________是因变量,______随____________的变化而变化;
(2)若出售2.5千克豆子,则总售价应为________元;
(3)根据你的预测,出售________千克豆子,可得总售价12元.
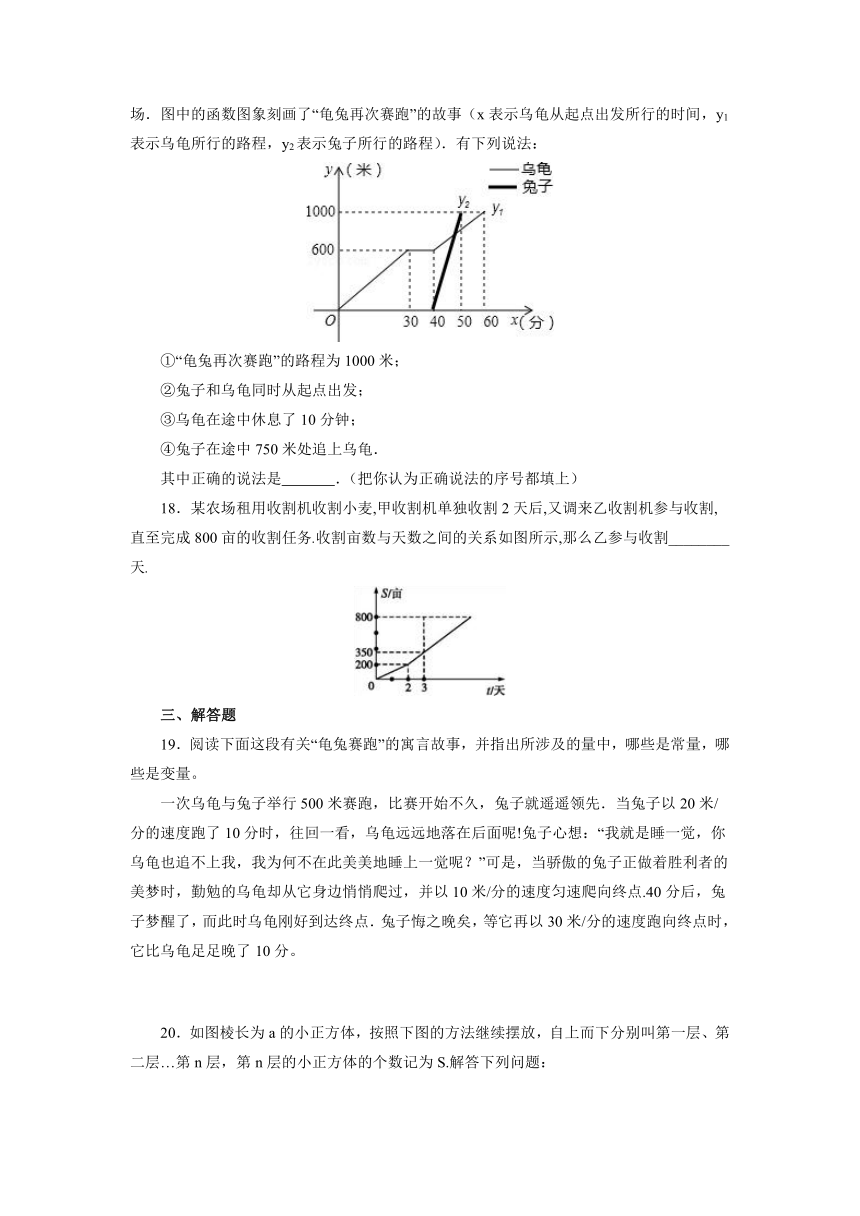
17.“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).有下列说法:
①“龟兔再次赛跑”的路程为1000米;
②兔子和乌龟同时从起点出发;
③乌龟在途中休息了10分钟;
④兔子在途中750米处追上乌龟.
其中正确的说法是 .(把你认为正确说法的序号都填上)
18.某农场租用收割机收割小麦,甲收割机单独收割2天后,又调来乙收割机参与收割,直至完成800亩的收割任务.收割亩数与天数之间的关系如图所示,那么乙参与收割________天.
三、解答题
19.阅读下面这段有关“龟兔赛跑”的寓言故事,并指出所涉及的量中,哪些是常量,哪些是变量。
一次乌龟与兔子举行500米赛跑,比赛开始不久,兔子就遥遥领先.当兔子以20米/分的速度跑了10分时,往回一看,乌龟远远地落在后面呢!兔子心想:“我就是睡一觉,你乌龟也追不上我,我为何不在此美美地睡上一觉呢?”可是,当骄傲的兔子正做着胜利者的美梦时,勤勉的乌龟却从它身边悄悄爬过,并以10米/分的速度匀速爬向终点.40分后,兔子梦醒了,而此时乌龟刚好到达终点.兔子悔之晚矣,等它再以30米/分的速度跑向终点时,它比乌龟足足晚了10分。
20.如图棱长为a的小正方体,按照下图的方法继续摆放,自上而下分别叫第一层、第二层…第n层,第n层的小正方体的个数记为S.解答下列问题:
n 1 2 3 4 …
S 1 3 …
(1)按要求填写上表:
(2)研究上表可以发现S随n的变化而变化,且S随n的增大而增大有一定的规律,请你用式子来表示S与n的关系,并计算当n=10时,S的值为多少?
21.近期,大陆相关部门对原产台湾地区的15种水果实施进口零关税措施,扩大了台湾水果在大陆的销售,某经销商销售了台湾水果凤梨,根据以往销售经验,每天的售价与销售量之间有如下关系:
每千克售价(元) 38 37 36 35 … 20
每天销量(千克) 50 52 54 56 … 86
设当单价从38元/千克下调了x元时,销售量为y千克.
(1)写出y与x之间的关系式;
(2)如果凤梨的进价是20元/千克,某天的销售价定为30元/千克,这天的销售利润是多少?
(3)以前在两岸未直接通航时,运输要绕行,需耗时一周(七天),凤梨最长的保存期为一个月(30天),若每天售价不低于30元/千克,一次进货最多只能是多少千克?
22.小明某天上午9时骑自行车离开家,15时回家,他有意描绘了离家的距离与时间的变化情况(如图).
(1)图象表示了哪两个变量的关系?哪个是自变量?哪个是因变量?
(2)10时和13时,他分别离家多远?
(3)他到达离家最远的地方是什么时间?离家多远?
(4)11时到12时他行驶了多少千米?
(5)他可能在哪段时间内休息,并吃午餐?
(6)他由离家最远的地方返回时的平均速度是多少?
23.如图,长方形ABCD中,AB=4,BC=8.点P在AB上运动,设PB=x,图中阴影部分的面积为y.
(1)写出阴影部分的面积y与x之间的函数解析式和自变量x的取值范围;
(2)点P在什么位置时,阴影部分的面积等于20?
24.已知池中有600m3的水,每小时抽50m3.
(1)写出剩余水的体积Vm3与时间th之间的函数表达式;
(2)写出自变量t的取值范围;
(3)8h后,池中还剩多少水?
(4)多长时间后,池中剩余100m3的水?
25.如图所示,A、B两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也于同日下午骑摩托车按相同路线从A地出发驶往B地,如图所示,图中的折线PQR和线段MN分别表示甲、乙所行驶的路程S和时间t的关系.象回答下列问题:
(1)甲和乙哪一个出发的更早 早出发多长时间
(2)甲和乙哪一个早到达B城 早多长时间
(3)乙骑摩托车的速度和甲骑自行车在全程的平均速度分别是多少
(4)请你根据图象上的数据,求出乙出发后多长时间追上甲
参考答案
一、选择题
1.A
2.C
3.C
4.B
5.C
6.A
7.D
8.B
9.A
10.C
二、填空题
11.
12.7.09
13.80
14.-40
15.72
16.所售豆子数量和总售价 总售价 总售价 所售豆子数量 5 6
17.①③④
18.4
三、解答题
19.500米、乌龟的速度10米/分等在整个变化过程中是常量,兔子的速度是变量。
20.(1)6,10(2)55
21.(1)y=50+2x;(2) 1518千克
22.(1) 自变量是时间,因变量是距离;(2) 10时他距家15千米,13时他距家30千米;
(3) 12:00时他到达离家最远的地方,离家30千米;(4)13千米;
(5) 12:00~13:00休息并吃午餐;(6) 15千米/时
23.(1)阴影部分的面积为:y=32-4x(0<x≤4);(2)PB=3
24.(1)V=600﹣50t;(2)0≤t≤12;(3)故8小时后,池中还剩200立方米水;(4)10小时后,池中还有100立方米的水.
25.(1)甲更早,早出发1 h;(2)乙更早,早到2 h;(3)甲的平均速度12.5km/h, 乙的平均速度是50km/h;(4) 乙出发0.5 h就追上甲
本章检测
满分:100分,限时:60分钟
一、选择题(每题3分,共30分)
1.在△ABC中,它的底边是a,底边上的高是h,则三角形面积S=ah,当a为定长时,在此函数关系式中( )
A.S,h是变量,,a是常量 B.S,h,a是变量,是常量
C.a,h是变量,,S是常量 D.S是变量,,a,h是常量
2.一列快车从甲地开往乙地,一列慢车从乙地开往甲地,两车同时出发,两车离乙地的路程s(千米)与行驶时间t(小时)的关系如图所示,则下列结论中错误的是( )
A.甲、乙两地的路程是400千米 B.慢车行驶速度为60千米/小时
C.相遇时快车行驶了150千米 D.快车出发后4小时到达乙地
3.A、B两地相距20千米,甲、乙两人都从A地去B地,图中和分别表示甲、乙两人所走路程(千米)与时刻(小时)之间的关系.下列说法:
①乙晚出发1小时;
②乙出发3小时后追上甲;
③甲的速度是4千米/小时;
④乙先到达B地.
其中正确的个数是( )
A.1 B.2 C.3 D.4
4.某商场自行车存放处每周的存车量为5000辆次,其中变速车存车费是每辆一次1元,普通车存车费为每辆一次0. 5元,若普通车存车量为辆次,存车的总收入为元,则与之间的关系式是( )
A. B.
C. D.
5.某科研小组在网上获取了声音在空气中传播的速度与空气温度关系的一些数据(如下表):
温度/℃ ﹣20 ﹣10 0 10 20 30
声速/m/s 318 324 330 336 342 348
下列说法错误的是( )
A.在这个变化中,自变量是温度,因变量是声速
B.温度越高,声速越快
C.当空气温度为20℃时,声音5s可以传播1740m
D.当温度每升高10℃,声速增加6m/s
6.如图所示的函数图象反映的过程是:小徐从家去菜地浇水,又去玉米地除草,然后回家.其中x表示时间,y表示小徐离他家的距离.读图可知菜地离小徐家的距离为( )
A.1.1千米 B.2千米 C.15千米 D.37千米
7.小亮家与姥姥家相距24 km,小亮8:00从家出发,骑自行车去姥姥家.妈妈8:30从家出发,乘车沿相同路线去姥姥家.在同一直角坐标系中,小亮和妈妈的行进路程s(km)与时间t(h)的函数图象如图所示.根据图象得出下列结论,其中错误的是( )
A.小亮骑自行车的平均速度是12 km/h
B.妈妈比小亮提前0.5 h到达姥姥家
C.妈妈在距家12 km处追上小亮
D.9:30妈妈追上小亮
8.李大爷要围成一个矩形菜园,菜园的一边利用足够长的墙,用篱笆围成的另外三边总长应恰好为24米.要围成的菜园是如图所示的矩形ABCD.设BC边的长为x米,AB边的长为y米,则y与x之间的函数关系式是( )
A.y=-2x+24(0
A. B.
C. D.
10.如图,下图是汽车行驶速度(千米/时)和时间(分)的关系图,下列说法其中正确的个数为( )
(1)汽车行驶时间为40分钟;(2)AB表示汽车匀速行驶;(3)在第30分钟时,汽车的速度是90千米/时;(4)第40分钟时,汽车停下来了.
A.1个 B.2个 C.3个 D.4个
二、填空题
11.函数中.自变量x的取值范围是______.
12.某型号汽油的数量与相应金额的关系如图,那么这种汽油的单价为每升________ 元.
13.小明从家跑步到学校,接着马上原路步行回家.如图所示为小明离家的路程与时间的图像,则小明回家的速度是每分钟步行________m.
14.同一温度的华氏度数y(℉)与摄氏度数x(℃)之间的函数解析式是y=x+32.若某一温度的摄氏度数值与华氏度数值恰好相等,则此温度的摄氏度数为__ __℃.
15.日常生活中,“老人”是一个模糊概念.可用“老人系数”表示一个人的老年化程度.“老人系数”的计算方法如下表:
人的年龄x(岁) x≤60 60<x<80 x≥80
“老人系数” 0 1
按照这样的规定,“老人系数”为0.6的人的年龄是__岁.
16.一种豆子在市场上出售,豆子的总售价与所售豆子的数量之间的关系如下表:
所售豆子数量/千克 0 0.5 1 1.5 2 2.5 3 3.5 4
总售价/元 0 1 2 3 4 5 6 7 8
(1)上表反映的变量是____________,________是因变量,______随____________的变化而变化;
(2)若出售2.5千克豆子,则总售价应为________元;
(3)根据你的预测,出售________千克豆子,可得总售价12元.
17.“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).有下列说法:
①“龟兔再次赛跑”的路程为1000米;
②兔子和乌龟同时从起点出发;
③乌龟在途中休息了10分钟;
④兔子在途中750米处追上乌龟.
其中正确的说法是 .(把你认为正确说法的序号都填上)
18.某农场租用收割机收割小麦,甲收割机单独收割2天后,又调来乙收割机参与收割,直至完成800亩的收割任务.收割亩数与天数之间的关系如图所示,那么乙参与收割________天.
三、解答题
19.阅读下面这段有关“龟兔赛跑”的寓言故事,并指出所涉及的量中,哪些是常量,哪些是变量。
一次乌龟与兔子举行500米赛跑,比赛开始不久,兔子就遥遥领先.当兔子以20米/分的速度跑了10分时,往回一看,乌龟远远地落在后面呢!兔子心想:“我就是睡一觉,你乌龟也追不上我,我为何不在此美美地睡上一觉呢?”可是,当骄傲的兔子正做着胜利者的美梦时,勤勉的乌龟却从它身边悄悄爬过,并以10米/分的速度匀速爬向终点.40分后,兔子梦醒了,而此时乌龟刚好到达终点.兔子悔之晚矣,等它再以30米/分的速度跑向终点时,它比乌龟足足晚了10分。
20.如图棱长为a的小正方体,按照下图的方法继续摆放,自上而下分别叫第一层、第二层…第n层,第n层的小正方体的个数记为S.解答下列问题:
n 1 2 3 4 …
S 1 3 …
(1)按要求填写上表:
(2)研究上表可以发现S随n的变化而变化,且S随n的增大而增大有一定的规律,请你用式子来表示S与n的关系,并计算当n=10时,S的值为多少?
21.近期,大陆相关部门对原产台湾地区的15种水果实施进口零关税措施,扩大了台湾水果在大陆的销售,某经销商销售了台湾水果凤梨,根据以往销售经验,每天的售价与销售量之间有如下关系:
每千克售价(元) 38 37 36 35 … 20
每天销量(千克) 50 52 54 56 … 86
设当单价从38元/千克下调了x元时,销售量为y千克.
(1)写出y与x之间的关系式;
(2)如果凤梨的进价是20元/千克,某天的销售价定为30元/千克,这天的销售利润是多少?
(3)以前在两岸未直接通航时,运输要绕行,需耗时一周(七天),凤梨最长的保存期为一个月(30天),若每天售价不低于30元/千克,一次进货最多只能是多少千克?
22.小明某天上午9时骑自行车离开家,15时回家,他有意描绘了离家的距离与时间的变化情况(如图).
(1)图象表示了哪两个变量的关系?哪个是自变量?哪个是因变量?
(2)10时和13时,他分别离家多远?
(3)他到达离家最远的地方是什么时间?离家多远?
(4)11时到12时他行驶了多少千米?
(5)他可能在哪段时间内休息,并吃午餐?
(6)他由离家最远的地方返回时的平均速度是多少?
23.如图,长方形ABCD中,AB=4,BC=8.点P在AB上运动,设PB=x,图中阴影部分的面积为y.
(1)写出阴影部分的面积y与x之间的函数解析式和自变量x的取值范围;
(2)点P在什么位置时,阴影部分的面积等于20?
24.已知池中有600m3的水,每小时抽50m3.
(1)写出剩余水的体积Vm3与时间th之间的函数表达式;
(2)写出自变量t的取值范围;
(3)8h后,池中还剩多少水?
(4)多长时间后,池中剩余100m3的水?
25.如图所示,A、B两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也于同日下午骑摩托车按相同路线从A地出发驶往B地,如图所示,图中的折线PQR和线段MN分别表示甲、乙所行驶的路程S和时间t的关系.象回答下列问题:
(1)甲和乙哪一个出发的更早 早出发多长时间
(2)甲和乙哪一个早到达B城 早多长时间
(3)乙骑摩托车的速度和甲骑自行车在全程的平均速度分别是多少
(4)请你根据图象上的数据,求出乙出发后多长时间追上甲
参考答案
一、选择题
1.A
2.C
3.C
4.B
5.C
6.A
7.D
8.B
9.A
10.C
二、填空题
11.
12.7.09
13.80
14.-40
15.72
16.所售豆子数量和总售价 总售价 总售价 所售豆子数量 5 6
17.①③④
18.4
三、解答题
19.500米、乌龟的速度10米/分等在整个变化过程中是常量,兔子的速度是变量。
20.(1)6,10(2)55
21.(1)y=50+2x;(2) 1518千克
22.(1) 自变量是时间,因变量是距离;(2) 10时他距家15千米,13时他距家30千米;
(3) 12:00时他到达离家最远的地方,离家30千米;(4)13千米;
(5) 12:00~13:00休息并吃午餐;(6) 15千米/时
23.(1)阴影部分的面积为:y=32-4x(0<x≤4);(2)PB=3
24.(1)V=600﹣50t;(2)0≤t≤12;(3)故8小时后,池中还剩200立方米水;(4)10小时后,池中还有100立方米的水.
25.(1)甲更早,早出发1 h;(2)乙更早,早到2 h;(3)甲的平均速度12.5km/h, 乙的平均速度是50km/h;(4) 乙出发0.5 h就追上甲
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
