2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册-6.1分类加分计数原理与分步乘法计数原理同步练习(Word含答案解析)
文档属性
| 名称 | 2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册-6.1分类加分计数原理与分步乘法计数原理同步练习(Word含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 185.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-18 18:20:43 | ||
图片预览


文档简介
人教A版选择性必修第三册第六章6.1《分类加分计数原理与分步乘法计数原理》
一、基础巩固
1.有3名防控新冠肺炎疫情的志愿者,每人从2个不同的社区中选择1个进行服务,则不同的选择方法共有
( )
A.12种 B.9种 C.8种 D.6种
2.将2封不同的信投入3个不同的信箱,不同的投法种数为( )
A. B.3 C. D.
3.为促进中学生综合素质全面发展,某校开设5个社团,甲、乙、丙三名同学每人只报名参加1个社团,则不同的报名方式共有( )
A.60种 B.120种 C.125种 D.243种
4.若4名学生报名参加数学、计算机、航模兴趣小组,每人选报1项,则不同的报名方式有( )
A.种 B.种 C.种 D.种
5.若自然数n使得做竖式加法均不产生进位现象,则称n为“可连数”,例如32是“可连数”,因为不产生进位现象;23不是“可连数”,因为产生了进位现象.那么小于200的“可连数”的个数为( )
A.18 B.20 C.22 D.24
6.一个的表格内,放有3辆完全相同的红车和3辆完全相同的黑车,每辆车占1格,每行每列只有1辆车,放法种数为( )
A.720 B.20 C.518400 D.14400
7.某校为庆祝元旦举办文艺汇演,原节目单上有7个节目已经排好顺序,现在有2个新节目需要加进去,不改变原来节目的先后顺序,则新节目单的排法有______种.
8.某公司招牌5名员工,分给下属的甲乙两个部门,其中2名英语翻译人员不能分给同一部门,另3名电脑编程人员不能都分给同一部门,则不同的分配方案种数是______.
9.书架的第1层放有4本不同的计算机书,第2层放有3本不同的文艺书,第3层放有2本不同的体育书.
(1)从书架上任取1本书,有多少种不同取法?
(2)从书架的第1层、第2层、第3层各取1本书,有多少种不同取法?
10.(1)如果,那么在平面直角坐标系内,集合中有多少个不同的点?
(2)如果,,那么在平面直角坐标系内,方程所表示的不同的直线共有多少条?
二、综合运用
11.某校为了庆祝新中国成立70周年举办文艺汇演,原节目单上有10个节目已经排好顺序,又有3个新节目需要加进去,不改变原来节目的顺序,则新节目单的排法有( )种
A.165 B.286 C.990 D.1716
12.如图所示,将四棱锥S-ABCD的每一个顶点染上一种颜色,并使同一条棱上的两端异色,如果只有5种色可供使用,则不同的染色方法种数为( )
A.240 B.360 C.420 D.960
13.(多选题)现有不同的黄球5个,黑球6个,蓝球4个,则下列说法正确的是( )
A.从中任选1个球,有15种不同的选法
B.若每种颜色选出1个球,有120种不同的选法
C.若要选出不同颜色的2个球,有31种不同的选法
D.若要不放回地选出任意的2个球,有240种不同的选法
14.(多选题)甲、乙、丙、丁、戊五只猴子在一棵枯树上玩耍,假设它们均不慎失足下落,已知:(1)甲在下落的过程中依次撞击到树枝A,B,C;(2)乙在下落的过程中依次撞击到树枝D,E,F;(3)丙在下落的过程中依次撞击到树枝G,A,C;(4)丁在下落的过程中依次撞击到树枝B,D,H;(5)戊在下落的过程中依次撞击到树枝I,C,E,则下列结论正确的是( )
A.最高处的树枝为G,I中的一个
B.最低处的树枝一定是F
C.这九根树枝从高到低不同的顺序共有33种
D.这九根树枝从高到低不同的顺序共有32种
三、拓广探究
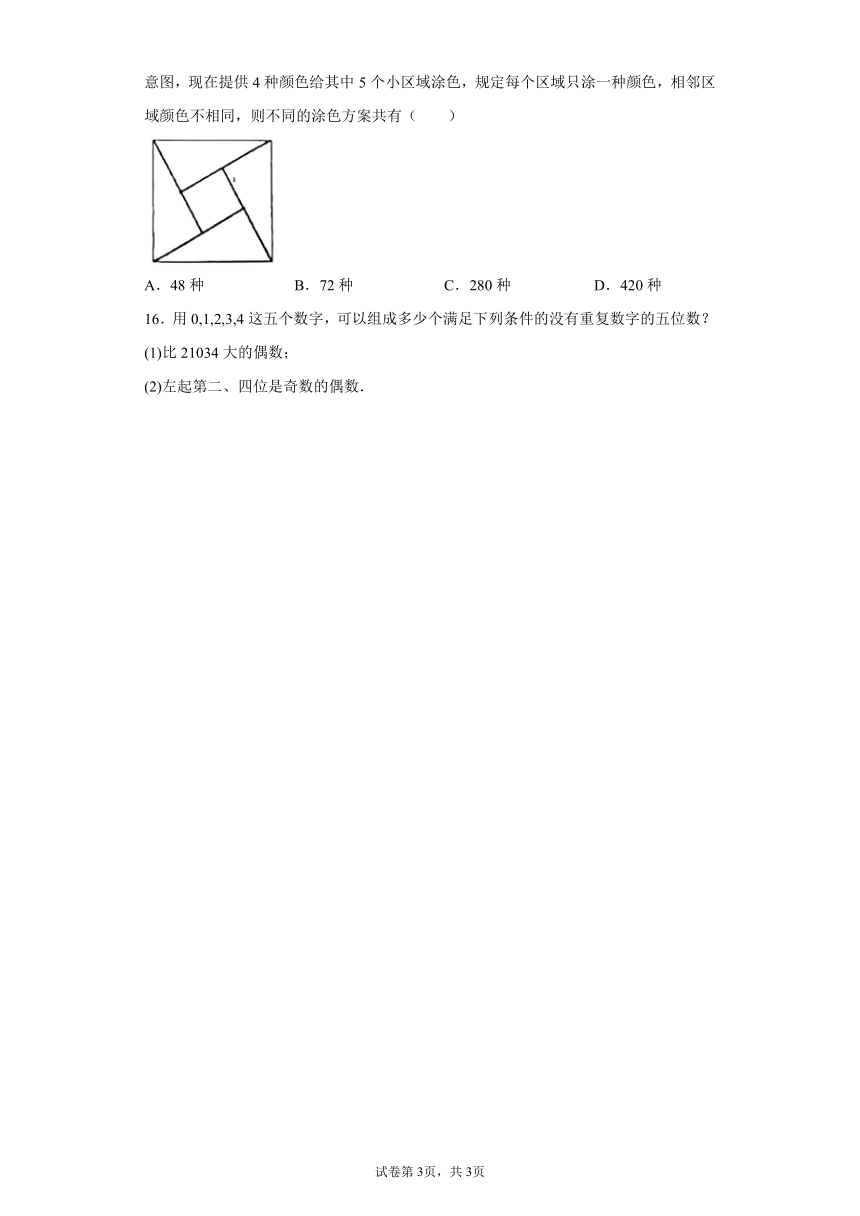
15.如图为我国数学家赵爽(约3世纪初)在为《周髀算经》作注时验证勾股定理的示意图,现在提供4种颜色给其中5个小区域涂色,规定每个区域只涂一种颜色,相邻区域颜色不相同,则不同的涂色方案共有( )
A.48种 B.72种 C.280种 D.420种
16.用0,1,2,3,4这五个数字,可以组成多少个满足下列条件的没有重复数字的五位数?
(1)比21034大的偶数;
(2)左起第二、四位是奇数的偶数.
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.C
每名防控新冠肺炎疫情的志愿者都有2种不同的选择方法,根据分步计数原理可知,不同的选择方法共有(种).
2.C
第一封信的投法有3种,第二封信的投法有3种,
∴根据分步计数原理可知一共有(种)投法.
3.C
由题意知,甲、乙、丙三名同学每人只报名参加1个社团,所以每个人有5种选择.则不同的报名方式共有(种),
4.A
4名学生,每人有三种可选方案,根据分步计数原理,4人共有种方法.
5.D
个位x需要满足:,即,x可取0,1,2三个数.
十位y需要满足:,即,y可取0,1,2,3四个数.
因为是小于200的“可连数”,故百位需要满足:小于2.则小于200的两位“可连数”的
个数为;小于200的两位“可连数”的个数为;小于200的一位“可
连数”的个数为3.故小于200的“可连数”的个数为.
6.D
先假设3辆红车不同,3辆黑车也不相同,
第一辆车显然可占36个方格中任意一个,有36种放法,
第二辆车由于不能与第一辆车同行,也不能与第一辆车同列,有25种放法,
同理,第三、四、五、六辆车分别有16,9,4,1种放法.
再注意到3辆红车相同,3辆黑车也相同,
故不同的放法共有(种).
7.72
第一步:从排好的7个节目中空出的8个位置,加入第1个新节目,有8种方法;
第二步:从排好的8个节目中空出的9个位置,加入第2个新节目,有9种方法.
由分步乘法计数原理得,共有种排法.
8.12
解:由题意可得,
①若甲部门要2名电脑编程人员,则有3种情况;2名英语翻译人员的分配方法有2种.根据分步乘法计数原理,分配方案共有(种).
②若甲部门要1名电脑编程人员,则有3种情况;2名英语翻译人员的分配方法有2种.根据分步乘法计数原理,分配方案有(种).由分类加法计数原理,可得不同的分配方案共有(种).
9.(1)
从书架上任取1本书,有三类方案:
第1类,从第1层取1本计算机书,有4种方法;
第2类,从第2层取1本文艺书,有3种方法;
第3类,从第3层取1本体育书,有2种方法.
根据分类加法计数原理,不同取法的种数为.
(2)
从书架的第1层、第2层、第3层各取1本书,可以分三步完成:
第1步,从第1层取1本计算机书,有4种方法;
第2步,从第2层取1本文艺书,有3种方法;
第3步,从第3层取1本体育书,有2种方法.
根据分步乘法计数原理,不同取法的种数为.
10.(1)36;(2)16
(1)根据题意,确定集合中的点,需分两步完成:
第1步,确定有6种方法;第2步,确定有6种方法;
根据分步乘法计数原理,不同取法的种数为.
所以集合中共有36个不同的点.
(2)根据题意,确定方程所表示的直线,需分两步完成:
第1步,确定斜率有4种方法;第2步,确定截距有4种方法;
根据分步乘法计数原理,不同取法的种数为.
所以方程所表示的不同的直线共有16条.
11.D
第一步:10个节目空出11个位置,加入1个新来的节目,所以加入一个新节目有11种方法,
第二步:从排好的11个节目空出的12个位置中,加入第2个新节目,有12种方法,
第三步:从排好的12个节目空出的13个位置中,加入第3个新节目,有13种方法,
所以由分步乘法计数原理得,加入3个新节目后的节目单的排法有(种).
12.C
由题设,四棱锥S-ABCD的顶点S、A、B所染的颜色互不相同,它们共有种染色方法.
设5种颜色为1,2,3,4,5,当S、A、B染好时,不妨设其颜色分别为1、2、3,
若C染2,则D可染3或4或5,有3种染法;
若C染4,则D可染3或5,有2种染法,若C染5,则D可染3或4,有2种染法.
可见,当S、A、B已染好时,C、D还有7种染法,故不同的染色方法有(种).
13.AB
解:对于A,从中任选1个球,共有种不同的选法,故A正确;
对于B,每种颜色选出1个球,可分步从每种颜色分别选择,共有种不同的选法,故B正确;
对于C,若要选出不同颜色的2个球,首先按颜色分三类“黄,黑”,“黄,蓝”,“黑,蓝”,再进行各类分步选择,共有种不同的选法,故C错误;
对于D,若要不放回地选出任意的2个球,直接分步计算,共有种不同的选法,故D错误.
14.AC
由题判断出部分树枝由高到低的顺序为,还剩下,,,且树枝比高,树枝在树枝,之间,树枝比低,最高可能为G或I,最低为F或H,故选项正确,B错误;
先看树枝,有4种可能,若在,之间,
则有3种可能:①在,之间,有5种可能;
②在,之间,有4种可能;
③在,之间,有3种可能,
此时树枝的高低顺序有(种)。
若不在,之间,则有3种可能,有2中可能,
若在,之间,则有3种可能,
若在,之间,则有三种可能,
此时树枝的高低顺序有(种)可能,
故这九根树枝从高到低不同的顺序共有种,故选项正确.
15.B
由题意可知,上下两块区域涂色可以相同,也可以不同,则共有的涂色方案数为:
16.(1)39(2)8
解:(1)根据题意,分3种情况讨论:
①当末位数字是0时,首位数字可以为2或3或4,满足条件的数共有18个.
②当末位数字是2时,首位数字可以为3或4,满足条件的数共有12个.
③当末位数字是4时,首位数字是3的有6个符合条件的数字,
首位数字是2时,有3个符合条件的数字,
此时共有9个符合条件的数字.
综上知,比21034大的偶数共有个;
(2)根据题意,有3步进行分析:
①第二、四位从奇数1,3中取,有2种情况;
②个位数字从2,4中取,有2种情况,
③余下的排在剩下的两位,有2种情况,
故共有个符合条件的数字.答案第1页,共2页
答案第1页,共2页
一、基础巩固
1.有3名防控新冠肺炎疫情的志愿者,每人从2个不同的社区中选择1个进行服务,则不同的选择方法共有
( )
A.12种 B.9种 C.8种 D.6种
2.将2封不同的信投入3个不同的信箱,不同的投法种数为( )
A. B.3 C. D.
3.为促进中学生综合素质全面发展,某校开设5个社团,甲、乙、丙三名同学每人只报名参加1个社团,则不同的报名方式共有( )
A.60种 B.120种 C.125种 D.243种
4.若4名学生报名参加数学、计算机、航模兴趣小组,每人选报1项,则不同的报名方式有( )
A.种 B.种 C.种 D.种
5.若自然数n使得做竖式加法均不产生进位现象,则称n为“可连数”,例如32是“可连数”,因为不产生进位现象;23不是“可连数”,因为产生了进位现象.那么小于200的“可连数”的个数为( )
A.18 B.20 C.22 D.24
6.一个的表格内,放有3辆完全相同的红车和3辆完全相同的黑车,每辆车占1格,每行每列只有1辆车,放法种数为( )
A.720 B.20 C.518400 D.14400
7.某校为庆祝元旦举办文艺汇演,原节目单上有7个节目已经排好顺序,现在有2个新节目需要加进去,不改变原来节目的先后顺序,则新节目单的排法有______种.
8.某公司招牌5名员工,分给下属的甲乙两个部门,其中2名英语翻译人员不能分给同一部门,另3名电脑编程人员不能都分给同一部门,则不同的分配方案种数是______.
9.书架的第1层放有4本不同的计算机书,第2层放有3本不同的文艺书,第3层放有2本不同的体育书.
(1)从书架上任取1本书,有多少种不同取法?
(2)从书架的第1层、第2层、第3层各取1本书,有多少种不同取法?
10.(1)如果,那么在平面直角坐标系内,集合中有多少个不同的点?
(2)如果,,那么在平面直角坐标系内,方程所表示的不同的直线共有多少条?
二、综合运用
11.某校为了庆祝新中国成立70周年举办文艺汇演,原节目单上有10个节目已经排好顺序,又有3个新节目需要加进去,不改变原来节目的顺序,则新节目单的排法有( )种
A.165 B.286 C.990 D.1716
12.如图所示,将四棱锥S-ABCD的每一个顶点染上一种颜色,并使同一条棱上的两端异色,如果只有5种色可供使用,则不同的染色方法种数为( )
A.240 B.360 C.420 D.960
13.(多选题)现有不同的黄球5个,黑球6个,蓝球4个,则下列说法正确的是( )
A.从中任选1个球,有15种不同的选法
B.若每种颜色选出1个球,有120种不同的选法
C.若要选出不同颜色的2个球,有31种不同的选法
D.若要不放回地选出任意的2个球,有240种不同的选法
14.(多选题)甲、乙、丙、丁、戊五只猴子在一棵枯树上玩耍,假设它们均不慎失足下落,已知:(1)甲在下落的过程中依次撞击到树枝A,B,C;(2)乙在下落的过程中依次撞击到树枝D,E,F;(3)丙在下落的过程中依次撞击到树枝G,A,C;(4)丁在下落的过程中依次撞击到树枝B,D,H;(5)戊在下落的过程中依次撞击到树枝I,C,E,则下列结论正确的是( )
A.最高处的树枝为G,I中的一个
B.最低处的树枝一定是F
C.这九根树枝从高到低不同的顺序共有33种
D.这九根树枝从高到低不同的顺序共有32种
三、拓广探究
15.如图为我国数学家赵爽(约3世纪初)在为《周髀算经》作注时验证勾股定理的示意图,现在提供4种颜色给其中5个小区域涂色,规定每个区域只涂一种颜色,相邻区域颜色不相同,则不同的涂色方案共有( )
A.48种 B.72种 C.280种 D.420种
16.用0,1,2,3,4这五个数字,可以组成多少个满足下列条件的没有重复数字的五位数?
(1)比21034大的偶数;
(2)左起第二、四位是奇数的偶数.
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.C
每名防控新冠肺炎疫情的志愿者都有2种不同的选择方法,根据分步计数原理可知,不同的选择方法共有(种).
2.C
第一封信的投法有3种,第二封信的投法有3种,
∴根据分步计数原理可知一共有(种)投法.
3.C
由题意知,甲、乙、丙三名同学每人只报名参加1个社团,所以每个人有5种选择.则不同的报名方式共有(种),
4.A
4名学生,每人有三种可选方案,根据分步计数原理,4人共有种方法.
5.D
个位x需要满足:,即,x可取0,1,2三个数.
十位y需要满足:,即,y可取0,1,2,3四个数.
因为是小于200的“可连数”,故百位需要满足:小于2.则小于200的两位“可连数”的
个数为;小于200的两位“可连数”的个数为;小于200的一位“可
连数”的个数为3.故小于200的“可连数”的个数为.
6.D
先假设3辆红车不同,3辆黑车也不相同,
第一辆车显然可占36个方格中任意一个,有36种放法,
第二辆车由于不能与第一辆车同行,也不能与第一辆车同列,有25种放法,
同理,第三、四、五、六辆车分别有16,9,4,1种放法.
再注意到3辆红车相同,3辆黑车也相同,
故不同的放法共有(种).
7.72
第一步:从排好的7个节目中空出的8个位置,加入第1个新节目,有8种方法;
第二步:从排好的8个节目中空出的9个位置,加入第2个新节目,有9种方法.
由分步乘法计数原理得,共有种排法.
8.12
解:由题意可得,
①若甲部门要2名电脑编程人员,则有3种情况;2名英语翻译人员的分配方法有2种.根据分步乘法计数原理,分配方案共有(种).
②若甲部门要1名电脑编程人员,则有3种情况;2名英语翻译人员的分配方法有2种.根据分步乘法计数原理,分配方案有(种).由分类加法计数原理,可得不同的分配方案共有(种).
9.(1)
从书架上任取1本书,有三类方案:
第1类,从第1层取1本计算机书,有4种方法;
第2类,从第2层取1本文艺书,有3种方法;
第3类,从第3层取1本体育书,有2种方法.
根据分类加法计数原理,不同取法的种数为.
(2)
从书架的第1层、第2层、第3层各取1本书,可以分三步完成:
第1步,从第1层取1本计算机书,有4种方法;
第2步,从第2层取1本文艺书,有3种方法;
第3步,从第3层取1本体育书,有2种方法.
根据分步乘法计数原理,不同取法的种数为.
10.(1)36;(2)16
(1)根据题意,确定集合中的点,需分两步完成:
第1步,确定有6种方法;第2步,确定有6种方法;
根据分步乘法计数原理,不同取法的种数为.
所以集合中共有36个不同的点.
(2)根据题意,确定方程所表示的直线,需分两步完成:
第1步,确定斜率有4种方法;第2步,确定截距有4种方法;
根据分步乘法计数原理,不同取法的种数为.
所以方程所表示的不同的直线共有16条.
11.D
第一步:10个节目空出11个位置,加入1个新来的节目,所以加入一个新节目有11种方法,
第二步:从排好的11个节目空出的12个位置中,加入第2个新节目,有12种方法,
第三步:从排好的12个节目空出的13个位置中,加入第3个新节目,有13种方法,
所以由分步乘法计数原理得,加入3个新节目后的节目单的排法有(种).
12.C
由题设,四棱锥S-ABCD的顶点S、A、B所染的颜色互不相同,它们共有种染色方法.
设5种颜色为1,2,3,4,5,当S、A、B染好时,不妨设其颜色分别为1、2、3,
若C染2,则D可染3或4或5,有3种染法;
若C染4,则D可染3或5,有2种染法,若C染5,则D可染3或4,有2种染法.
可见,当S、A、B已染好时,C、D还有7种染法,故不同的染色方法有(种).
13.AB
解:对于A,从中任选1个球,共有种不同的选法,故A正确;
对于B,每种颜色选出1个球,可分步从每种颜色分别选择,共有种不同的选法,故B正确;
对于C,若要选出不同颜色的2个球,首先按颜色分三类“黄,黑”,“黄,蓝”,“黑,蓝”,再进行各类分步选择,共有种不同的选法,故C错误;
对于D,若要不放回地选出任意的2个球,直接分步计算,共有种不同的选法,故D错误.
14.AC
由题判断出部分树枝由高到低的顺序为,还剩下,,,且树枝比高,树枝在树枝,之间,树枝比低,最高可能为G或I,最低为F或H,故选项正确,B错误;
先看树枝,有4种可能,若在,之间,
则有3种可能:①在,之间,有5种可能;
②在,之间,有4种可能;
③在,之间,有3种可能,
此时树枝的高低顺序有(种)。
若不在,之间,则有3种可能,有2中可能,
若在,之间,则有3种可能,
若在,之间,则有三种可能,
此时树枝的高低顺序有(种)可能,
故这九根树枝从高到低不同的顺序共有种,故选项正确.
15.B
由题意可知,上下两块区域涂色可以相同,也可以不同,则共有的涂色方案数为:
16.(1)39(2)8
解:(1)根据题意,分3种情况讨论:
①当末位数字是0时,首位数字可以为2或3或4,满足条件的数共有18个.
②当末位数字是2时,首位数字可以为3或4,满足条件的数共有12个.
③当末位数字是4时,首位数字是3的有6个符合条件的数字,
首位数字是2时,有3个符合条件的数字,
此时共有9个符合条件的数字.
综上知,比21034大的偶数共有个;
(2)根据题意,有3步进行分析:
①第二、四位从奇数1,3中取,有2种情况;
②个位数字从2,4中取,有2种情况,
③余下的排在剩下的两位,有2种情况,
故共有个符合条件的数字.答案第1页,共2页
答案第1页,共2页
