河北省石家庄市高邑县2021-2022学年八年级上学期期末数学试题(word版含答案)
文档属性
| 名称 | 河北省石家庄市高邑县2021-2022学年八年级上学期期末数学试题(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-17 22:23:31 | ||
图片预览


文档简介
高邑县2021—2022学年度第一学期期末教师教学质量监测
八年级数学试卷
考生须知 1.本试卷共4页,共三道大题,26个小题,满分120分。 2.在答题卡上准确填写学校、姓名,考号等相关信息。 3.试卷答案一律填涂或书写在答题卡上,在试卷上作答无效。 4.在答题卡上,选择题、作图题用2B铅笔作答,其它试题用黑色字迹签字笔作答。 5.考试结束,将试卷和答题卡一并交回。
一、选择题(本大题共16个小题,1—10小题,每小题3分;11—16小题,每小题2分,共42分.在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确答案填涂到答题纸上.)
1.下列图形中轴对称图形的个数有( )
A.4个 B.3个 C.2个 D.1个
2.若在实数范围内有意义,则x的取值范围是( )
A. B. C. D.
3.与结果相同的是( )
A. B. C. D.
4.下列二次根式中与是同类二次根式的是( )
A. B. C. D.
5.若取1.442,计算的结果是( )
A. B. C. D.
6.下列分式变形中,正确的是( )
A. B. C. D.
7.若,则代数式的值为( )
A.5 B. C. D.
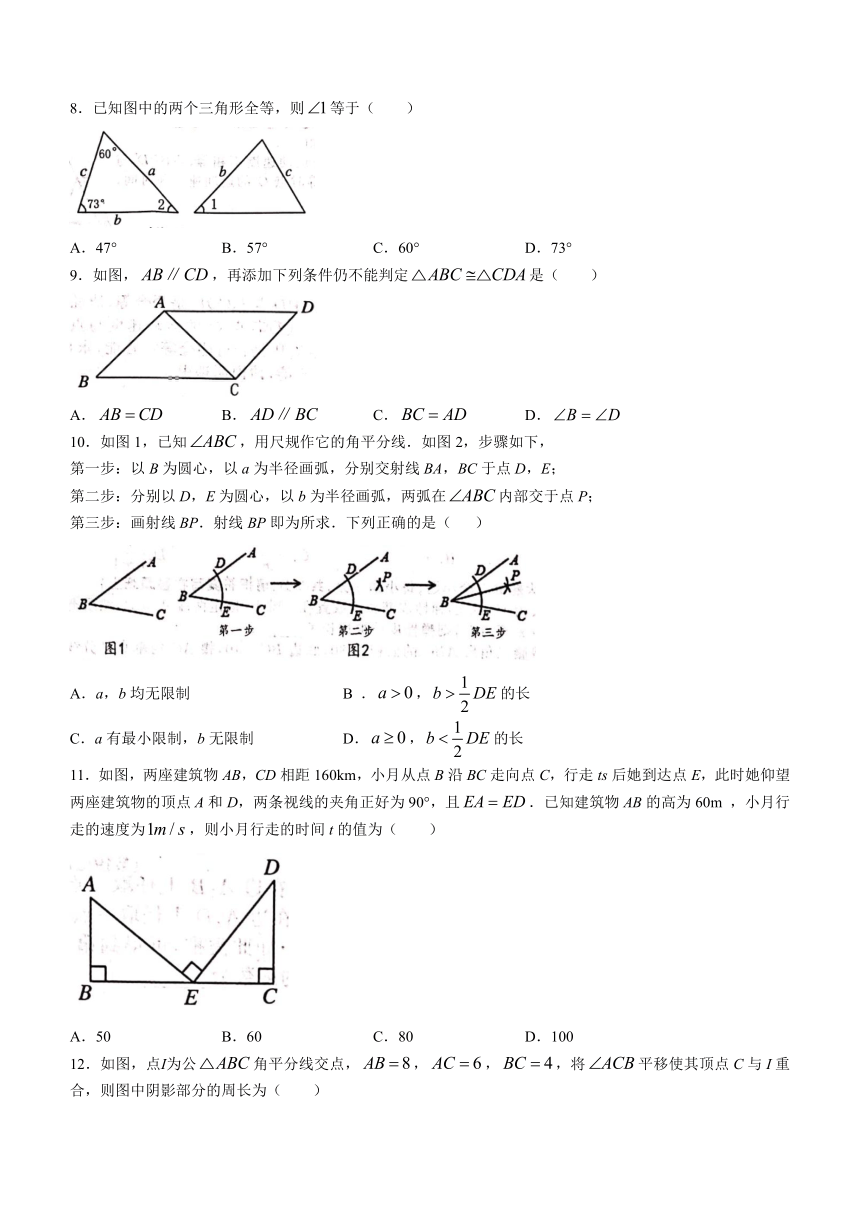
8.已知图中的两个三角形全等,则等于( )
A.47° B.57° C.60° D.73°
9.如图,,再添加下列条件仍不能判定是( )
A. B. C. D.
10.如图1,已知,用尺规作它的角平分线.如图2,步骤如下,
第一步:以B为圆心,以a为半径画弧,分别交射线BA,BC于点D,E;
第二步:分别以D,E为圆心,以b为半径画弧,两弧在内部交于点P;
第三步:画射线BP.射线BP即为所求.下列正确的是( )
A.a,b均无限制 B .,的长
C.a有最小限制,b无限制 D.,的长
11.如图,两座建筑物AB,CD相距160km,小月从点B沿BC走向点C,行走ts后她到达点E,此时她仰望两座建筑物的顶点A和D,两条视线的夹角正好为90°,且.已知建筑物AB的高为60m ,小月行走的速度为,则小月行走的时间t的值为( )
A.50 B.60 C.80 D.100
12.如图,点Ⅰ为公角平分线交点,,,,将平移使其顶点C与I重合,则图中阴影部分的周长为( )
A.4 B.6 C.8 D.10
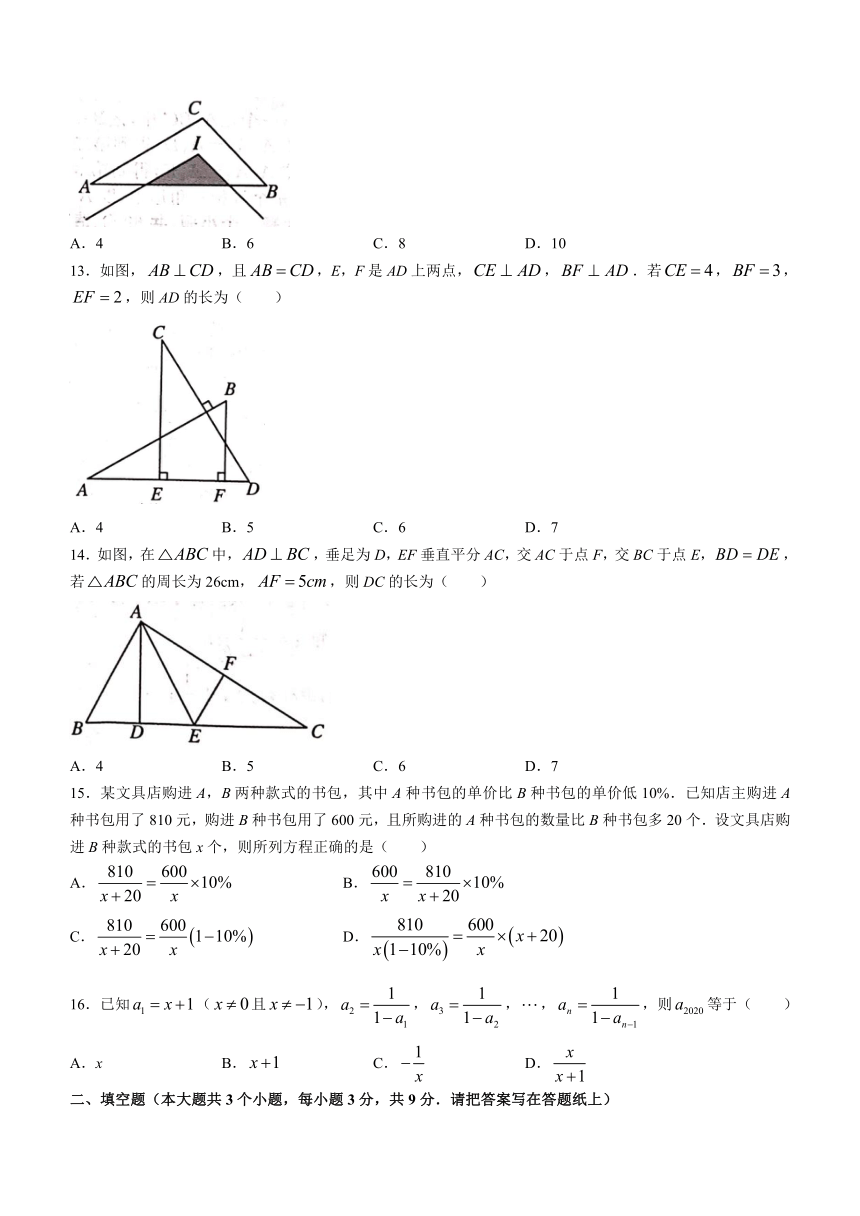
13.如图,,且,E,F是AD上两点,,.若,,,则AD的长为( )
A.4 B.5 C.6 D.7
14.如图,在中,,垂足为D,EF垂直平分AC,交AC于点F,交BC于点E,,若的周长为26cm,,则DC的长为( )
A.4 B.5 C.6 D.7
15.某文具店购进A,B两种款式的书包,其中A种书包的单价比B种书包的单价低10%.已知店主购进A种书包用了810元,购进B种书包用了600元,且所购进的A种书包的数量比B种书包多20个.设文具店购进B种款式的书包x个,则所列方程正确的是( )
A. B.
C. D.
16.已知(且),,,,,则等于( )
A.x B. C. D.
二、填空题(本大题共3个小题,每小题3分,共9分.请把答案写在答题纸上)
17.如图,长为12 cm的弹性皮筋拉直放置在一轴上,固定两端A和B,然后把中点C向上拉升8 cm至点D,则弹性皮筋被拉长了______.
18.如图,等腰三角形ABC的面积为80,底边,腰AC的垂直平分线EF交AC,AB于点E,F,若D为BC边中点,M为线段EF上一动点,则的周长最小值为______.
19.如图在第二个中,,,在边上任取一点D,延长到,使,得到第二个,再在边上任取一点E,延长到,使,得到第3个……如此类推,可得到第n个等腰三角形.则第n个等腰三角形中,以为顶点的内角的度数为______.
三、解答题(本大题7个小题,共69分.请写出解答步骤)
20.(本题2个小题,每小题5分,共10分.)
(1)解分式方程
(2)若,先化简再求值
21.(本题2个小题,每小题5分,共10分)
已知.
(1)求代数式;
(2)求的值.
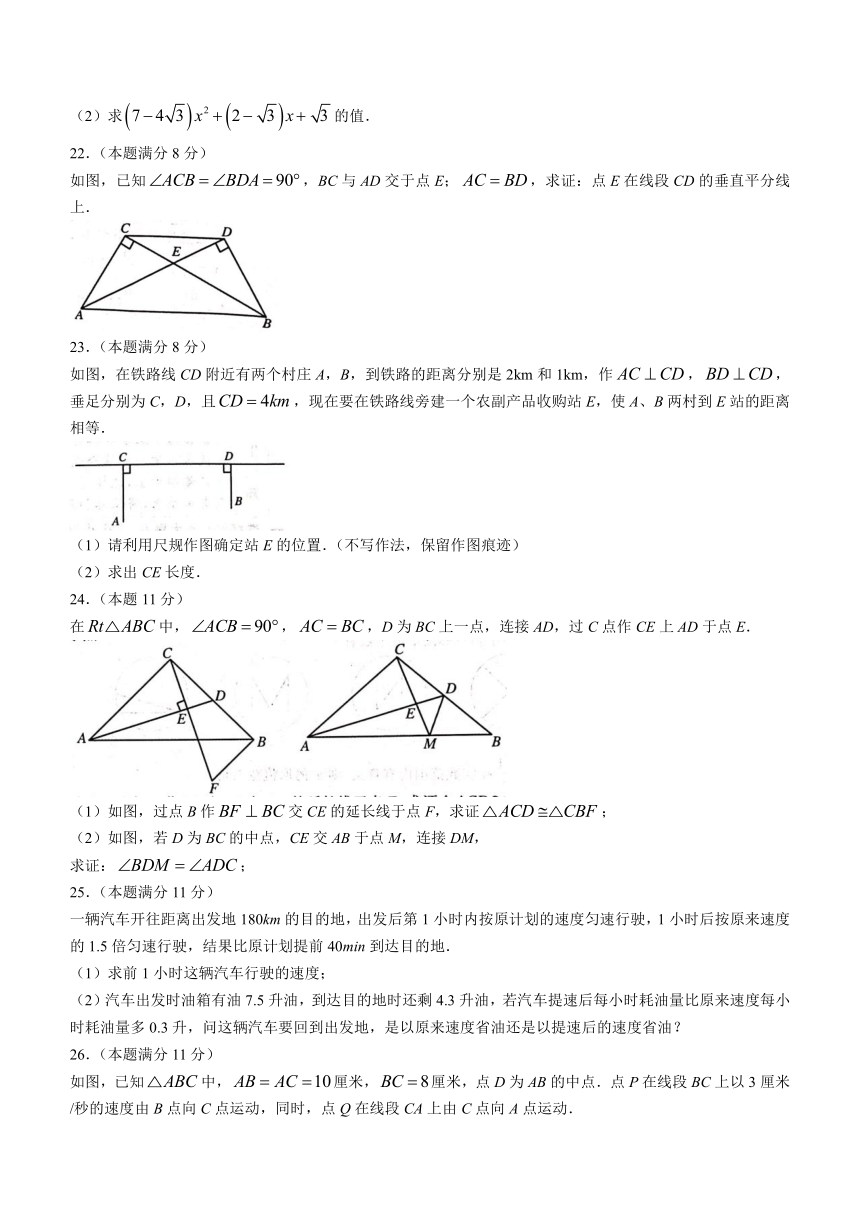
22.(本题满分8分)
如图,已知,BC与AD交于点E;,求证:点E在线段CD的垂直平分线上.
23.(本题满分8分)
如图,在铁路线CD附近有两个村庄A,B,到铁路的距离分别是2km和1km,作,,垂足分别为C,D,且,现在要在铁路线旁建一个农副产品收购站E,使A、B两村到E站的距离相等.
(1)请利用尺规作图确定站E的位置.(不写作法,保留作图痕迹)
(2)求出CE长度.
24.(本题11分)
在中,,,D为BC上一点,连接AD,过C点作CE上AD于点E.
(1)如图,过点B作交CE的延长线于点F,求证;
(2)如图,若D为BC的中点,CE交AB于点M,连接DM,
求证:;
25.(本题满分11分)
一辆汽车开往距离出发地180km的目的地,出发后第1小时内按原计划的速度匀速行驶,1小时后按原来速度的1.5倍匀速行驶,结果比原计划提前40min到达目的地.
(1)求前1小时这辆汽车行驶的速度;
(2)汽车出发时油箱有油7.5升油,到达目的地时还剩4.3升油,若汽车提速后每小时耗油量比原来速度每小时耗油量多0.3升,问这辆汽车要回到出发地,是以原来速度省油还是以提速后的速度省油?
26.(本题满分11分)
如图,已知中,厘米,厘米,点D为AB的中点.点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,与是否全等,请说明理由;
(2)若点Q的运动速度与点P的运动速度不相等,与是否可能全等?若能,求出全等时点Q的运动速度和时间;若不能,请说明理由.
2021—2022学年度第一学期期末考试八年级
数学试题参考答案及评分标准
一、选择题
题号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
答案 C B A D B D B A C B D C B B C B
二、填空题
17. 8 cm 18. 21 19.
三、解答题
20.(本题2个小题,每小题5分,共10分.)
(1)解:去分母得 ,
解得 ,
经检验是原方程的解 ,
∴原方程的解是;
(2)解:由且得,
,
,,
,
原式=
,
把代入得,
原式==-4048.
21.(本题2个小题,每小题5分,共10分)
解:(1),
则,
;
(2)
.
22.(本题满分8分)
证明:
∵,,且,
∴(HL), ……………………………4分
∴,,
∴,
∴,
∴点在线段的垂直平分线上. ……………………………8分
23.(本题满分8分)
解:(1)如图所示:点E即为所求; ……………………………2分
(2)连接AE、BE,
设CE=xkm,则DE=(4﹣x)km,
∵AC⊥CD,BD⊥CD,
∴△ACE和△BDE都是直角三角形,
在Rt△ACE中,AE2=22+x2,
在Rt△BDE中,BE2=12+(4﹣x)2
由(1)得:AE=BE,
∴22+x2=12+(4﹣x)2, ……………………………6分
解得:,
∴E点在距离C点处. ……………………………8分
24.(本题满分11分)
解:(1)证明:∵,,
∴,
∴,
∴,
又∵,
∴; ……………………………5分
(2)证明:过点作交的延长线于点,……………………………6分
如图所示:
由(1)得:,
∴,, ……………………………7分
∵为的中点,
∴,
∴,
∵,,
∴,
∵,
∴,
∴,
又∵,
∴, ……………………………10分
∴,
∴. ……………………………11分
25.(本题满分11分)
解:(1)设前1小时行驶的速度为,则1小时后行驶的速度为,
依题意,得: , ……………………………3分
解得:,
经检验,是原方程的解,且符合题意.
答:前1小时行驶的速度为. ……………………………5分
(2)设以原来速度行驶每小时耗油y升,则提速后每小时耗油升,
依题意,得:
解得:, ……………………………8分
∴回来时若以原速度行驶总耗油(升),
若以提速后的速度行驶总耗油(升).
∵,
∴以提速后的速度行驶更省油. ……………………………11分
26.(本题满分11分)
解:(1)∵秒,
∴厘米,
∵厘米,点为的中点,
∴厘米.
又∵厘米,
∴厘米,
∴.
又∵,
∴,
在△BPD和△CQP中
∴△BPD≌△CQP ……………………………5分
(2)△BPD与△CQP可能全等. ……………………………6分
∵,
∴, ……………………………7分
又∵△BPD与△CQP全等,
,
则, ……………………………9分
∴点,点运动的时间秒,
∴厘米/秒. ……………………………11分
八年级数学试卷
考生须知 1.本试卷共4页,共三道大题,26个小题,满分120分。 2.在答题卡上准确填写学校、姓名,考号等相关信息。 3.试卷答案一律填涂或书写在答题卡上,在试卷上作答无效。 4.在答题卡上,选择题、作图题用2B铅笔作答,其它试题用黑色字迹签字笔作答。 5.考试结束,将试卷和答题卡一并交回。
一、选择题(本大题共16个小题,1—10小题,每小题3分;11—16小题,每小题2分,共42分.在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确答案填涂到答题纸上.)
1.下列图形中轴对称图形的个数有( )
A.4个 B.3个 C.2个 D.1个
2.若在实数范围内有意义,则x的取值范围是( )
A. B. C. D.
3.与结果相同的是( )
A. B. C. D.
4.下列二次根式中与是同类二次根式的是( )
A. B. C. D.
5.若取1.442,计算的结果是( )
A. B. C. D.
6.下列分式变形中,正确的是( )
A. B. C. D.
7.若,则代数式的值为( )
A.5 B. C. D.
8.已知图中的两个三角形全等,则等于( )
A.47° B.57° C.60° D.73°
9.如图,,再添加下列条件仍不能判定是( )
A. B. C. D.
10.如图1,已知,用尺规作它的角平分线.如图2,步骤如下,
第一步:以B为圆心,以a为半径画弧,分别交射线BA,BC于点D,E;
第二步:分别以D,E为圆心,以b为半径画弧,两弧在内部交于点P;
第三步:画射线BP.射线BP即为所求.下列正确的是( )
A.a,b均无限制 B .,的长
C.a有最小限制,b无限制 D.,的长
11.如图,两座建筑物AB,CD相距160km,小月从点B沿BC走向点C,行走ts后她到达点E,此时她仰望两座建筑物的顶点A和D,两条视线的夹角正好为90°,且.已知建筑物AB的高为60m ,小月行走的速度为,则小月行走的时间t的值为( )
A.50 B.60 C.80 D.100
12.如图,点Ⅰ为公角平分线交点,,,,将平移使其顶点C与I重合,则图中阴影部分的周长为( )
A.4 B.6 C.8 D.10
13.如图,,且,E,F是AD上两点,,.若,,,则AD的长为( )
A.4 B.5 C.6 D.7
14.如图,在中,,垂足为D,EF垂直平分AC,交AC于点F,交BC于点E,,若的周长为26cm,,则DC的长为( )
A.4 B.5 C.6 D.7
15.某文具店购进A,B两种款式的书包,其中A种书包的单价比B种书包的单价低10%.已知店主购进A种书包用了810元,购进B种书包用了600元,且所购进的A种书包的数量比B种书包多20个.设文具店购进B种款式的书包x个,则所列方程正确的是( )
A. B.
C. D.
16.已知(且),,,,,则等于( )
A.x B. C. D.
二、填空题(本大题共3个小题,每小题3分,共9分.请把答案写在答题纸上)
17.如图,长为12 cm的弹性皮筋拉直放置在一轴上,固定两端A和B,然后把中点C向上拉升8 cm至点D,则弹性皮筋被拉长了______.
18.如图,等腰三角形ABC的面积为80,底边,腰AC的垂直平分线EF交AC,AB于点E,F,若D为BC边中点,M为线段EF上一动点,则的周长最小值为______.
19.如图在第二个中,,,在边上任取一点D,延长到,使,得到第二个,再在边上任取一点E,延长到,使,得到第3个……如此类推,可得到第n个等腰三角形.则第n个等腰三角形中,以为顶点的内角的度数为______.
三、解答题(本大题7个小题,共69分.请写出解答步骤)
20.(本题2个小题,每小题5分,共10分.)
(1)解分式方程
(2)若,先化简再求值
21.(本题2个小题,每小题5分,共10分)
已知.
(1)求代数式;
(2)求的值.
22.(本题满分8分)
如图,已知,BC与AD交于点E;,求证:点E在线段CD的垂直平分线上.
23.(本题满分8分)
如图,在铁路线CD附近有两个村庄A,B,到铁路的距离分别是2km和1km,作,,垂足分别为C,D,且,现在要在铁路线旁建一个农副产品收购站E,使A、B两村到E站的距离相等.
(1)请利用尺规作图确定站E的位置.(不写作法,保留作图痕迹)
(2)求出CE长度.
24.(本题11分)
在中,,,D为BC上一点,连接AD,过C点作CE上AD于点E.
(1)如图,过点B作交CE的延长线于点F,求证;
(2)如图,若D为BC的中点,CE交AB于点M,连接DM,
求证:;
25.(本题满分11分)
一辆汽车开往距离出发地180km的目的地,出发后第1小时内按原计划的速度匀速行驶,1小时后按原来速度的1.5倍匀速行驶,结果比原计划提前40min到达目的地.
(1)求前1小时这辆汽车行驶的速度;
(2)汽车出发时油箱有油7.5升油,到达目的地时还剩4.3升油,若汽车提速后每小时耗油量比原来速度每小时耗油量多0.3升,问这辆汽车要回到出发地,是以原来速度省油还是以提速后的速度省油?
26.(本题满分11分)
如图,已知中,厘米,厘米,点D为AB的中点.点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,与是否全等,请说明理由;
(2)若点Q的运动速度与点P的运动速度不相等,与是否可能全等?若能,求出全等时点Q的运动速度和时间;若不能,请说明理由.
2021—2022学年度第一学期期末考试八年级
数学试题参考答案及评分标准
一、选择题
题号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
答案 C B A D B D B A C B D C B B C B
二、填空题
17. 8 cm 18. 21 19.
三、解答题
20.(本题2个小题,每小题5分,共10分.)
(1)解:去分母得 ,
解得 ,
经检验是原方程的解 ,
∴原方程的解是;
(2)解:由且得,
,
,,
,
原式=
,
把代入得,
原式==-4048.
21.(本题2个小题,每小题5分,共10分)
解:(1),
则,
;
(2)
.
22.(本题满分8分)
证明:
∵,,且,
∴(HL), ……………………………4分
∴,,
∴,
∴,
∴点在线段的垂直平分线上. ……………………………8分
23.(本题满分8分)
解:(1)如图所示:点E即为所求; ……………………………2分
(2)连接AE、BE,
设CE=xkm,则DE=(4﹣x)km,
∵AC⊥CD,BD⊥CD,
∴△ACE和△BDE都是直角三角形,
在Rt△ACE中,AE2=22+x2,
在Rt△BDE中,BE2=12+(4﹣x)2
由(1)得:AE=BE,
∴22+x2=12+(4﹣x)2, ……………………………6分
解得:,
∴E点在距离C点处. ……………………………8分
24.(本题满分11分)
解:(1)证明:∵,,
∴,
∴,
∴,
又∵,
∴; ……………………………5分
(2)证明:过点作交的延长线于点,……………………………6分
如图所示:
由(1)得:,
∴,, ……………………………7分
∵为的中点,
∴,
∴,
∵,,
∴,
∵,
∴,
∴,
又∵,
∴, ……………………………10分
∴,
∴. ……………………………11分
25.(本题满分11分)
解:(1)设前1小时行驶的速度为,则1小时后行驶的速度为,
依题意,得: , ……………………………3分
解得:,
经检验,是原方程的解,且符合题意.
答:前1小时行驶的速度为. ……………………………5分
(2)设以原来速度行驶每小时耗油y升,则提速后每小时耗油升,
依题意,得:
解得:, ……………………………8分
∴回来时若以原速度行驶总耗油(升),
若以提速后的速度行驶总耗油(升).
∵,
∴以提速后的速度行驶更省油. ……………………………11分
26.(本题满分11分)
解:(1)∵秒,
∴厘米,
∵厘米,点为的中点,
∴厘米.
又∵厘米,
∴厘米,
∴.
又∵,
∴,
在△BPD和△CQP中
∴△BPD≌△CQP ……………………………5分
(2)△BPD与△CQP可能全等. ……………………………6分
∵,
∴, ……………………………7分
又∵△BPD与△CQP全等,
,
则, ……………………………9分
∴点,点运动的时间秒,
∴厘米/秒. ……………………………11分
同课章节目录
