2021—2022学年人教版九年级数学上册第22章二次函数复习学案
文档属性
| 名称 | 2021—2022学年人教版九年级数学上册第22章二次函数复习学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-18 09:36:12 | ||
图片预览




文档简介
二次函数
第一节:二次函数的定义
定义:一般地,形如(a,b,c是常数,a≠0)的函数,叫做二次函数.其中,x是自变量,a,b,c分别是函数解析式的二次项系数、一次项系数和常数项.
例1 当m 取何值时,函数是关于x 的二次函数?并求出这时二次函数的解析式.
题型1 二次函数的定义
1.下列函数是二次函数的是( )
A.y=x(x+1) B.x2y=1 C.y=2x3﹣2(x﹣1)2 D.y=x﹣0.5
2.下列函数中是二次函数的是( )
A. B. C. D.
3.下列函数中,一定是二次函数的是( )
A. B. C. D.
4.若y=(2-m)是二次函数,则m等于( )
A.±2 B.2 C.-2 D.不能确定
4.已知函数y=(k+2)是关于x的二次函数,则k=________.
5.若是二次函数,则m的值为________.
6. 已知函数
(1)当m为何值时,此函数为二次函数
(2)当m为何值时,此函数为一次函数
题型2 二次函数的一般式及函数值
二次函数的二次项系数为 ,一次项系数为 ,常数项为 。
把下列二次函数化为一般形式,并指出其二次项、一次项系数及常数项
(2)
(4)
题型3 利用二次函数模型解决实际问题
9.如图,在中,,,点从点沿边、匀速运动到点,过点作交于点,线段,,,则能够反映与之间函数关系的图象大致是( )
A. B.C.D.
第二节:二次函数的函数图象和性质
1、二次函数(a ≠ 0)的图象与性质
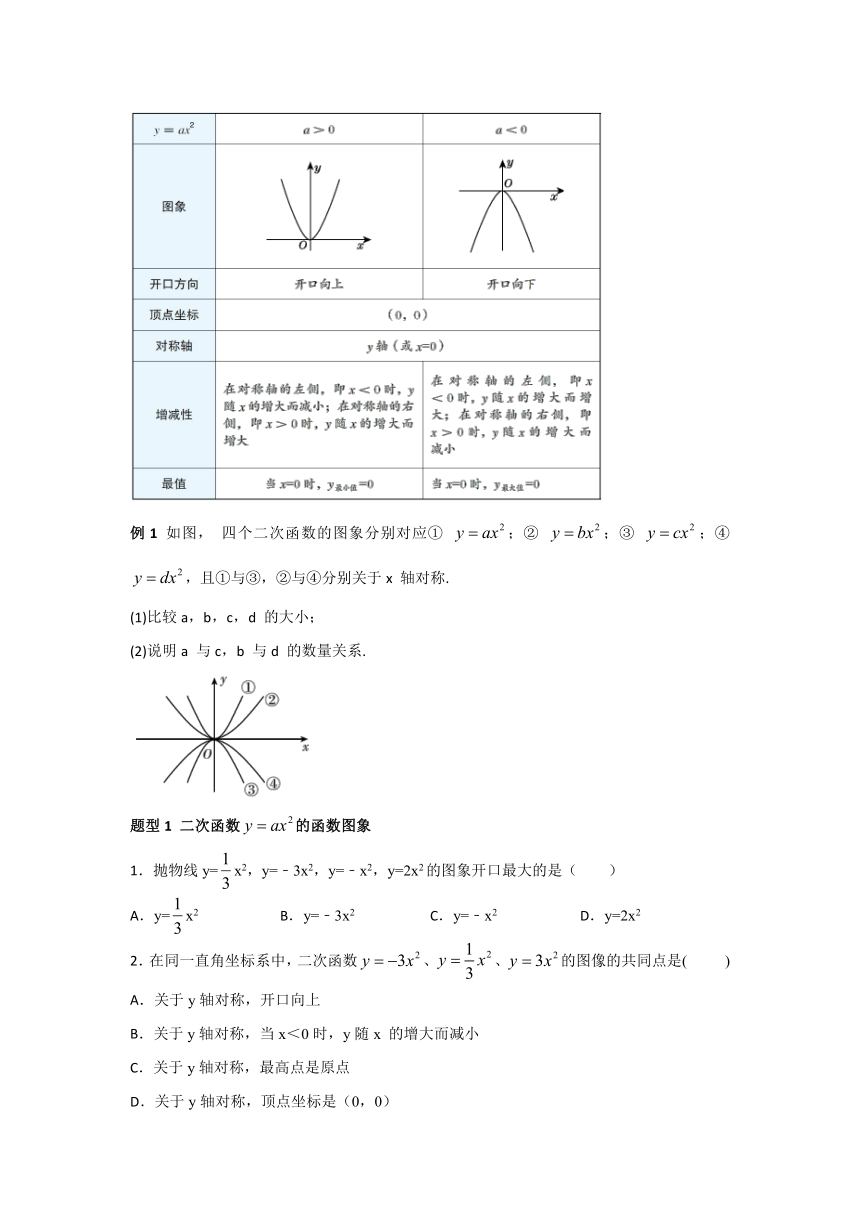
例1 如图, 四个二次函数的图象分别对应① ;② ;③ ;④ ,且①与③,②与④分别关于x 轴对称.
(1)比较a,b,c,d 的大小;
(2)说明a 与c,b 与d 的数量关系.
题型1 二次函数的函数图象
1.抛物线y=x2,y=﹣3x2,y=﹣x2,y=2x2的图象开口最大的是( )
A.y=x2 B.y=﹣3x2 C.y=﹣x2 D.y=2x2
2.在同一直角坐标系中,二次函数、、的图像的共同点是( )
A.关于y轴对称,开口向上
B.关于y轴对称,当x<0时,y随x 的增大而减小
C.关于y轴对称,最高点是原点
D.关于y轴对称,顶点坐标是(0,0)
3.函数y=ax-2 (a≠0).与y=ax2(a≠0)在同一平面直角坐标系中的图象可能是
A. B. C. D.
4.已知 a≠0,在同一坐标系中,y=ax与y=ax2的图象有可能是( )
A. B. C. D.
5.如图所示四个二次函数的图象中,分别对应的是①y=ax2;②y=bx2;③y=cx2;④y=dx2.则a、b、c、d的大小关系为_____.
6.如图,⊙O的半径为2,C1是函数y=x2的图象,C2是函数y=-x2的图象,则阴影部分的面积是________.
7.如图,垂直于x轴的直线AB分别与抛物线C1:y=x2(x≥0)和抛物线C2:y=(x≥0)交于A,B两点,过点A作CD∥x轴分别与y轴和抛物线C2交于点C、D,过点B作EF∥x轴分别与y轴和抛物线C1交于点E、F,则 的值为_____.
题型2 求待定系数问题
8.若抛物线y=ax2经过点A (,-9),则其解析式为_______________.
9.已知二次函数,如果当x=-1时y=2,那么当x=2时,y=_____.
10.二次函数有最低点,则m=__________
题型3 比较函数值大小
11.已知点(-2,),(0,),(1,)都在函数的图象上,则( )
A.>> B.>>
C.>> D.>>
12.已知a<-1,点(a-1,y1),(a,y2),(a+1,y3)都在函数y=x2的图象上,则( )
A.y113.二次函数,点在函数图像上,当时,_(填“﹥”或“﹤”).
题型4 利用函数性质解决问题
14.函数的部分对应值如下表:
… 0 1 2 …
… 2 0 2 …
根据表格回答:
(1)_________, ________;
(2)函数的解析式为 _________,定义域是 ________;
(3)请再举一些对应值,猜测该函数的图像关于________轴对称.
15. 已知函数是关于x 的二次函数.
(1)求满足条件的m 的值.
(2)当m 为何值时,其图象有最低点?求出这个最低点的坐标,这时当x 为何值时,y 随x 的增大而增大?
(3)当m 为何值时,函数有最大值?最大值是多少?这时当x为何值时,y 随x 的增大而减小?
16. 如图,已知函数与的交点为A,B(A在B的右边).
(1)求点A、点B的坐标; (2)连接,,求的面积.
第三节:二次函数的函数图象和性质
1、二次函数 的图象与二次函数 的图象的关系它们的形状(开口大小、方向)相同,只是上、下位置不同,二次函数的图象可由二次函数的图象上下平移|k| 个单位长度得到.
题型1 二次函数的图像及性质
1.抛物线y=x2+1的图象大致是( )
A. B. C. D.
2.二次函数y=-x2-1的图象大致是( )
A. B. C. D.
3.在同一坐标中,一次函数y=﹣kx+2与二次函数y=x2+k的图象可能是( )
A. B. C. D.
4.抛物线 的顶点坐标为(0,1),则抛物线的解析式为( )
A. B. C. D.
5.函数y=x2-4的图象与y轴的交点坐标是( )
A.(2,0) B.(-2,0) C.(0,4) D.(0,-4)
6.二次函数图像的对称轴是( ).
A.直线x=0 B.直线x=2 C.直线x=4 D.直线x= 4
7.点均在抛物线上,下列说法正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
8.下列点中,一定在二次函数y=x2﹣1图象上的是( )
A.(0,0) B.(1,1) C.(1,0) D.(0,1)
9.若二次函数的图像经过点、,则、的大小关系是( )
A. B. C. D.不能确定
10.二次函数y=﹣2x2﹣1图象的顶点坐标为( )
A.(0,0) B.(0,﹣1) C.(﹣2,﹣1) D.(﹣2,1)
11. 如图抛物线经过正方形OBAC的顶点A,B,C,则c= .
12. 已知抛物线具有如下性质:该抛物线上任意一点到定点的距离与到x轴的距离始终相等。如图,点M的坐标为,P是抛物线上的一个动点,则周长的最小值是 。
题型2 二次函数与二次函数的
13.二次函数y=x2的图象向上平移3个单位,得到新的图象的二次函数表达式是( ).
A. B. C. D.
14. 能否通过上下平移二次函数的图像,使得新得到的函数图像过点(3,-3)?若能,说出平移的方向和距离;若不能,说明理由。
15. 已知抛物线,当1≤x ≤5时,y的最大值是________ .
16. 已知抛物线,当时,y的最大值是 .
17. 已知:抛物线与直线交于点(m,3).
(1)求m和n的值;
(2)试说出抛物线的顶点坐标和对称轴;
(3)当x何值时,二次函数中y随x的增大而减小;
(4)函数与的图象是否还存在其它交点,若存在,请求出交点坐标;若没有,请说明理由.
第四节:二次函数的函数图象和性质
1. 二次函数的图象与二次函数 的图象的关系它们的形状(开口大小、方向)相同,只是左、右位置不同,二次函数 的图象可由二次函数的图象左右平移|h| 个单位长度得到.
题型1 二次函数的函数图象和性质
1.抛物线顶点坐标是
A. B. C. D.
2.在一次函数y=kx+b(k≠0)中,y随x的增大而减小,则二次函数y=k(x﹣1)2的图象大致是( )
A. B. C. D.
3.已知A(-4,y1),B(-3,y2),C(3,y3)三点都在二次函数y=-2(x+2)2的图象上,则y1,y2,y3的大小关系为___.
4. 已知A(,y1),B(1,y2),C(4,y3)三点都在二次函数y=﹣(x﹣2)2的图象上,则y1,y2,y3的大小关系为( )
A.y1<y2<y3 B.y1<y3<y2 C.y3<y1<y2 D.y3<y2<y1
题型2 二次函数与之间的关系
5.函数的图象可以由函数的图象( )得到
A.向左平移3个单位 B.向右平移3个单位
C.向上平移3个单位 D.向下平移3个单位
6. 抛物线向左平移3个单位长度,所得到的抛物线所对应的函数解析式为( )
7. 如图,坐标平面内有一顶点为A的抛物线,此抛物线与直线交于B,C两点,为正三角形,若A点的坐标为(-3,0),则此抛物线与y轴的交点坐标是 。
8.如图,Rt△OAB中,∠OAB=90°,O为坐标原点,边OA在x轴上,OA=AB=1个单位长度.把Rt△OAB沿x轴正方向平移1个单位长度后得△AA1B.
(1)求以A为顶点,且经过点B1的抛物线的解析式;
(2)若(1)中的抛物线与OB交于点C,与y轴交于点D,求点D、C的坐标.
第五节:二次函数的函数图象和性质
题型1 二次函数的函数图象和性质
1.二次函数y=﹣(x-2)2+1的图象中,若y随x的增大而减小,则x的取值范围是( )
A.x<2 B.x>2 C.x<﹣2 D.x>﹣2
2.二次函数 y=(x﹣2)2+3,当 0≤x≤5 时,y 的取值范围为( )
A.3≤y≤12 B.2≤y≤12 C.7≤y≤12 D.3≤y≤7
3.如果点是抛物线上两个不同的点,那么的值为( )
A.4 B.5 C.6 D.7
4.对于抛物线y=﹣(x+2)2+3,下列结论中正确结论的个数为( )
①抛物线的开口向下; ②对称轴是直线x=﹣2;
③图象不经过第一象限; ④当x>2时,y随x的增大而减小.
A.4 B.3 C.2 D.1
5.二次函数,当时,y随x的增大而增大,则m的取值范围是_____________
6.若二次函数y=a(x+h)2+k的图象经过(-3,0),(5,0)两点,则h的值为________
题型2 二次函数的平移
将抛物线向右平移2个单位长度,再向上平移1个单位长度,所得抛物线对应的函数解析式为( )
8. 不论取任何实数,抛物线的顶点都( ).
在直线上 B.在直线上
C.在直线上 D.不确定
9. 已知二次函数y=(x-2a)2+(a-1)(a为常数),当a取不同的值时,其图象构成一个“抛物线系”.如图分别是当a=-1,a=0,a=1,a=2时二次函数的图象.它们的顶点在一条直线上,这条直线的解析式是____________________.
10.如图,在平面直角坐标系中,O是坐标原点,点A的坐标是,过点A作轴,垂足为B,连接,抛物线经过点A,与x轴正半轴交于点C.
(1)求c的值;
(2)将抛物线向下平移m个单位,使平移后得到的抛物线顶点落在的内部(不包括的边界),求m的取值范围.
题型3 函数值大小比较
11.已知点A(x1,y1),B(x2,y2)在二次函数y=(x-1)2+1的图象上.若x1>x2>1,则y1________y2(填“>”“<”或“=”).
12.已知点A(4,y1),B(,y2),C(-2,y3)都在二次函数y=(x-2)2-1的图象上,则y1,y2,y3的大小关系是 .
13. 如图,抛物线与轴交于,两点在的左侧),与轴交于点,点与关于抛物线的对称轴对称.
(1)求抛物线的解析式及点的坐标;
(2)点是抛物线上的一点,当的面积是8,求出点的坐标;
(3)过直线下方的抛物线上一点作轴的平行线,与直线交于点,已知点的横坐标是,试用含的式子表示的长及△ADM的面积,并求当的长最大时的值.
第六节:二次函数的函数图象和性质
二次函数的各项系数的符号与图象位置间的关系:
(1)a决定抛物线的开口方向,简记为“正上负下”;
(2)c决定抛物线与y轴的交点位置,简记为“上正下负原点0”;
(3)a、b的符号共同决定对称轴x=的位置,简记为:“左同右异y轴0”;可以由各项系数的符号来决定图象的位置,也可以由图象的位置来判断各项系数的符号.
题型1 二次函数的函数图象和性质
1.抛物线的顶点坐标是( )
A. B. C. D.
2.二次函数的顶点和对称轴分别是 ( )
A.,直线x=1 B.,直线x=4
C.,直线 D.,直线
3.若二次函数的图像对称轴为直线经过不同的5点,,,,,则,,的大小关系( )
A. B. C. D.
4.点P(m,n)在以y轴为对称轴的二次函数y=x2+ax+4的图象上.则m﹣n的最大值等于( )
A. B.4 C.﹣ D.﹣
5.已知关于x的二次函数y=x2+(2-a)x+5,当1≤x≤3时,y在x=1时取得最大值,则实数a的取值范围是( )
A.a≥2 B.a≤-2 C.a≥6 D.a<0
题型2 二次函数与二次函数之间的转换
6.二次函数图象的顶点坐标是 .
7.已知抛物线的顶点坐标为(3,-1),则b=_____,c=______.
8.指出下列函数的开口方向、对称轴、顶点坐标和变化情况
(1)
(2)
9.已知二次函数的图像过抛物线的顶点和坐标原点.
(1)求二次函数的解析式
(2)判断点A(-2,5)是否在这个二次函数的图像上 .
10.抛物线y=﹣x2+(m-1)x+m与y轴交于(0,3)点,
(1)求m的值;
(2)当x取何值时,抛物线在x轴的上方.
题型3 二次函数的图像与之间的关系
11.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①a+b+c<0;②b2﹣4ac>0;③b>0;④4a﹣2b+c<0;⑤a+c<,其中正确结论的个数是( )
A.②③④ B.①②⑤ C.①②④ D.②③⑤
12.已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论中正确的是( )
A.abc>0 B.b2﹣4ac<0 C.9a+3b+c>0 D.c+8a<0
13.如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,直线x=-1是对称轴,有下列判断:①b-2a=0;②4a-2b+c<0;③a-b+c=-9a;④若(-3,y1),(,y2)是抛物线上两点,则y1>y2,其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
专题1 二次函数解析式的求法
待定系数法求二次函数解析式
用一般式(三点式)确定二次函数解析式
1.已知二次函数图像经过下列点,求二次函数的解析式:
(1)(0,-1),(1,-1),(2,3)
(2)(0,0),(2,0),(-3,3)
2.已知二次函数图像经过下列点,求二次函数的解析式:
(1)(0,-1),(1,-1),(2,3)
(2)(0,0),(2,0),(-3,3)
用顶点式确定二次函数解析式
若抛物线的顶点是,且经过,则抛物线的函数解析式为
二次函数的图象的顶点在坐标轴上,则的值为__________.
5.已知抛物线顶点为(2,3),且经过(1,2)求二次函数解析式.
用交点式确定二次函数解析式
抛物线与x轴交与,B(- 3,0)两点,求该抛物线的解析式
利用对称确定二次函数解析式
已知抛物线的对称轴为直线并且与x轴的一个交点为(3,0),那么它所对应的函数解析式是 。
利用平移求二次函数解析式
7.将抛物线的图象绕着顶点旋转后得到的抛物线是_____________
8.将抛物线绕顶点旋转,则旋转后的抛物线的解析式为( )
A. B.
C. D.
9.将抛物线的图象绕原点旋转,则旋转后的抛物线的函数关系式( )
A. B. C. D.
10.二次函数的图像以x轴为对称轴翻折,翻折后它的函数解析式是_____.
利用直线与二次函数交点求解解析式
11.二次函数与直线的图象交于点
求,的值;
写出二次函数的表达式,并指出取何值时该表达式随的增大而增大?
写出该抛物线的顶点坐标和对称轴
12.如图,抛物线y=ax2+bx过点P(﹣1,5),A(4,0).
(1)求抛物线的解析式;
(2)在第一象限内的抛物线上有一点B,当PA⊥PB时,求点B的坐标.
13.一次函数与二次函数的图象的一个交点坐标是,另一个交点是该二次函数图象的顶点.
(1)求k,a,c的值.
(2)过点A(0,m)(0由表格信息求二次函数解析式
14.下表是二次函数y=ax2+bx+c的x,y的部分对应值:
x … 0 1 2 …
y … ﹣1 m ﹣1 n …
则对于该函数的性质的判断:①该二次函数有最大值;②不等式y>﹣1的解集是x<0或x>2;③方程ax2+bx+c=0的两个实数根分别位于﹣<x<0和2<x<之间;④当x>0时,函数值y随x的增大而增大;其中正确的是( )
A.②③ B.②④ C.①③ D.③④
15.二次函数(a,b,c为常数且a≠0)中的与的部分对应值如下表:
0 1 3
3 5 3
现给出如下四个结论:①;② 当时,的值随值的增大而减小;③是方程的一个根;④当时,,其中正确结论的序号为:__ __.
16.已知二次函数y=ax2+bx+c(a≠0)中,函数值y与自变量x的部分对应值如表:
x … ﹣5 ﹣4 ﹣3 ﹣2 ﹣1 …
y … 3 ﹣2 ﹣5 ﹣6 ﹣5 …
则关于x的一元二次方程ax2+bx+c=3的根是_____.
17.已知二次函数y=ax2+bx+c(a≠0)自变量x的值和它对应的函数值y如表所示:
(1)请写出该二次函数图象的开口方向、对称轴、顶点坐标和m的值;
(2)设该二次函数图象与x轴的左交点为B,它的顶点为A,该图象上点C的横坐标为4,求△ABC的面积.
18.根据学习函数的经验,探究函数y=x2+ax﹣4|x+b|+4(b<0)的图象和性质:
(1)下表给出了部分x,y的取值;
x L ﹣3 ﹣2 ﹣1 0 1 2 3 4 5 L
y L 3 0 ﹣1 0 3 0 ﹣1 0 3 L
由上表可知,a= ,b= ;
(2)用你喜欢的方式在坐标系中画出函数y=x2+ax﹣4|x+b|+4的图象;
(3)结合你所画的函数图象,写出该函数的一条性质;
(4)若方程x2+ax﹣4|x+b|+4=x+m至少有3个不同的实数解,请直接写出m的取值范围.
几何应用中求二次函数解析式
19. 已知,如图抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
(1)求抛物线的解析式;
20. 如图,抛物线交X轴于A、B两点,交Y轴于点C ,,求抛物线的解析式;
专题2 二次函数图像与系数之间的关系
1.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①3a+b<0;②a﹣b+c<0;③c>0;④a+b>0.其中正确的结论有( )
A.仅①②③ B.仅②③④
C.仅①②④ D.①②③④
2.二次函数y=ax2+bx+c的图象如图所示,则下列命题中:①b=﹣2a;②此抛物线向下移动c个单位后过点(2,0);③﹣1<a<﹣;④方程x2﹣2x+=0有实数根,结论正确的个数( )
A.1个 B.2个 C.3个 D.4个
3.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:
①abc>0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤a+b>m(am+b)(m≠1的实数).
其中正确的结论有( )
A.2个 B.3个 C.4个 D.5个
4.在同一直角坐标系中,函数和函数(m是常数,且)的图象可能是( )
A.B.C. D.
5.已知是非零实数,,在同一平面直角坐标系中,二次函数与一次函数的大致图象不可能是( )
A. B. C. D.
专题3 二次函数与一元二次方程和不等式之间的关系
二次函数与一元二次方程之间的关系
1.已知二次函数(m为常数)的图象与x轴的一个交点为,则关于x的一元二次方程的两实数根分别是( )
A. B. C. D.
2.若抛物线经过第四象限的点),则关于x的方程的根的情况是( )
A.有两个大于1的不相等实数根 B.有两个小于1的不相等实数根
C.有一个大于1另一个小于1的实数根 D.没有实数根
3.抛物线与x轴只有一个公共点,则m的值为________.
4.抛物线经过、两点,若关于的一元二次方程的一个解为,则__________.
5.已知关于x的一元二次方程有两个不相等的实数根.
(1)求k的取值范围;
(2)若k取小于1的整数,且此方程的解为整数,则求出此方程的两个整数根;
(3)在(2)的条件下,二次函数与x轴交于A、B两点(A点在B点的左侧),D点在此抛物线的对称轴上,若∠DAB=60 ,直接写出D点的坐标.
二次函数与不等式之间的关系
6.抛物线的部分图象如图所示,若,则的取值范围是( )
B.或 C.或 D.
7.如图,一次函数y1=kx+n(k≠0)与二次函数y2=ax2+bx+c(a≠0)的图象相交于A(﹣1,5)、B(9,2)两点,则关于x的不等式kx+n≥ax2+bx+c的解集为( )
A.﹣1≤x≤9 B.﹣1≤x<9 C.﹣1<x≤9 D.x≤﹣1或x≥9
8.如图,抛物线和直线,当时,的取值范围是( )
B.或 C.或 D.
9.抛物线y=﹣x2+bx+c的部分图象如图所示,若y>0,则x的取值范围是_____.
10.如图,二次函数的图象的顶点C的坐标为,与x轴交于,根据图象回答下列问题:
(1)写出方程的根;
(2)写出不等式的解集.
专题4 二次函数与几何结合问题
二次函数中的距离最值问题
1. P是抛物线上一点,过点P作PM⊥x轴,PN⊥y轴,垂足分别是M,N,则PM+PN的最小值是( )
A. B. C.3 D.5
2.如图,抛物线与x轴交于A,B两点,其中点A的坐标为,与y轴交于点C,点在抛物线上.
(1)求抛物线的解析式;
(2)抛物线的对称轴上有一动点P,求出的最小值;
(3)若抛物线上有一动点Q,使的面积为6,求点Q的坐标.
3.如图,在平面直角坐标系上,一条抛物线y=ax2+bx+c(a≠0)经过A(1,0)、B(3,0)、C(0,3)三点,连接BC并延长.
(1)求抛物线的解析式;
(2)点M是直线BC在第一象限部分上的一个动点,过M作MN∥y轴交抛物线于点N.
①求线段MN的最大值;
②当MN取最大值时,在线段MN右侧的抛物线上有一个动点P,连接PM、PN,当△PMN的外接圆圆心Q在△PMN的边上时,求点P的坐标.
二次函数中几何面积/周长最值问题
4.已知二次函数的图象以(-1,4)为顶点,且过点(2,-5),x轴交点为A,B,(A在B左侧).与y轴交于点C,
(1)求该函数的关系式;
(2)求△ABC的面积.
(3)若在抛物线上有一点M,使△ABM的面积是△ABC的面积的2倍,求M点坐标.
5.如图,抛物线y=ax2+bx+3(a≠0)的对称轴为直线x=﹣1,抛物线交x轴于A、C两点,与直线y=x﹣1交于A、B两点,直线AB与抛物线的对称轴交于点E.
(1)求抛物线的解析式.
(2)点P在直线AB上方的抛物线上运动,若△ABP的面积最大,求此时点P的坐标.
(3)在平面直角坐标系中,以点B、E、C、D为顶点的四边形是平行四边形,请直接写出符合条件点D的坐标.
6.如图1,抛物线与轴交于点,对称轴与抛物线交于点,与轴交于点.
(1)求抛物线的解析式.
(2)点是轴上的动点,求的最小周长.
(3)如图2,点是抛物线上一个动点,分别与交于点.
①若动点在第一象限,问的值是否发生变化.若不变,求出其值;若发生变化,请说明理由.
②若动点在第二象限,请给出①中类似的关于与长的结论(不必证明).
二次函数中的存在问题
7.直线与x轴y轴分别交于点A,B,抛物线经过点A,B,并与x轴交于另一点C,其顶点为P,
(1)求的值;
(2)抛物线的对称轴上有一点Q,使是以AB为底边的等腰三角形,求点Q的坐标;
8.如图,抛物线与x轴交于A(-1,0),B(5 ,0)两点,直线与y轴交于点C,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m.
(1)求抛物线的解析式;
(2)若PE=3+4EF,求m的值;
(3)是否存在点P,使得△PCE与△DEF相似.若存在,求出点P的坐标,若不存在,请说明理由.
9.如图,抛物线y=ax2+bx+c(a≠0)的图象经过A(1,0),B(3,0),C(0,6)三点.
(1)求抛物线的解析式.
(2)抛物线的顶点M与对称轴l上的点N关于x轴对称,直线AN交抛物线于点D,直线BE交AD于点E,若直线BE将△ABD的面积分为1:2两部分,求点E的坐标.
(3)P为抛物线上的一动点,Q为对称轴上动点,抛物线上是否存在一点P,使A、D、P、Q为顶点的四边形为平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
10.综合与探究
如图,抛物线经过点A(-2,0),B(4,0)两点,与轴交于点C,点D是抛物线上一个动点,设点D的横坐标为.连接AC,BC,DB,DC,
(1)求抛物线的函数表达式;
(2)△BCD的面积等于△AOC的面积的时,求的值;
(3)在(2)的条件下,若点M是轴上的一个动点,点N是抛物线上一动点,试判断是否存在这样的点M,使得以点B,D,M,N为顶点的四边形是平行四边形,若存在,请直接写出点M的坐标;若不存在,请说明理由.
利用直线平移与二次函数图像交点情况求字母取值范围
【中考.菏泽】如图,在平面直角坐标系中,抛物线过,两点。
求抛物线的解析式;
记抛物线顶点为D,求的面积;
若直线向上平移c个单位所得直线与抛物线段BCD(包括两个端点B,C)部分有两个交点,求c的取值范围。
专题5二次函数实际问题
题型1 利用二次函数解决销售利润中的最值问题
求最大利润问题
例1.某超市购进一批成本为每件元的商品,经调查发现,该商品每天的销售量(件)与销售单价(元)之间满足一次函数关系,其图象如图所示.
(1)求该商品每天的销售量与销售单价之间的函数关系式;
(2)若超市按单价不低于成本价,且不高于元销售,则销售单价定为多少,才能使销售该商品每天获得的利润(元)最大
(3)若超市要使销售该商品每天获得的利润为元,则每天的销售量应为多少件
例2.某商店销售一种销售成本为40元/千克的水产品,若按50元/千克销售,一个月可售出500千克,销售价每涨价1元,月销售量就减少10千克.
(1)写出月销售利润(单位:元)与售价(单位:元/千克)之间的函数关系式.
(2)商场将在月销售成本不超过3000元的情况下,使得月销售利润达到8000元,销售单价应定为多少?
(3)当售价定为多少元时,会获得最大利润?求出最大利润.
例3.某超市销售一种文具,进价为5元/件.售价为6元/件时,当天的销售量为100件.在销售过程中发现:售价每上涨0.5元,当天的销售量就减少5件.设当天销售单价统一为元/件(,且是按0.5元的倍数上涨),当天销售利润为元.
(1)求与的函数关系式(不要求写出自变量的取值范围);
(2)要使当天销售利润不低于240元,求当天销售单价所在的范围;
(3)若每件文具的利润不超过,要想当天获得利润最大,每件文具售价为多少元?并求出最大利润.
例4.某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,经试销发现,销售量(件)与销售单价(元)符合一次函数,且时,;时,.
(1)求一次函数的表达式;
(2)若该商场获得利润为元,试写出利润与销售单价之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
(3)若该商场获得利润不低于500元,试确定销售单价的范围.
优选销售方案
例5.某商场要经营一种新上市的文具,进价为20元,试营销阶段发现:当销售单价是25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件
(1)写出商场销售这种文具,每天所得的销售利润(元)与销售单价(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大;
(3)商场的营销部结合上述情况,提出了A、B两种营销方案
方案A:该文具的销售单价高于进价且不超过30元;
方案B:每天销售量不少于10件,且每件文具的利润至少为25元
请比较哪种方案的最大利润更高,并说明理由
例6.浩然文具店新到一种计算器,进价为25元,营销时发现:当销售单价定为30元时,每天的销售量为150件,若销售单价每上涨1元,每天的销售量就会减少10件.
(1)写出商店销售这种计算器,每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式;
(2)求销售单价定为多少元时,每天的销售利润最大?最大值是多少?
(3)商店的营销部结合上述情况,提出了A、B两种营销方案:
方案A:为了让利学生,该计算器的销售利润不超过进价的24%;
方案B:为了满足市场需要,每天的销售量不少于120件.
请比较哪种方案的最大利润更高,并说明理由.
题型2 利用建立二次函数模型解决实际中抛物线型最值问题
投球问题
例7.在一次篮球比赛中,如图队员甲正在投篮.已知球出手时离地面m,与篮圈中心的水平距离为7 m,球出手后水平距离为4 m时达到最大高度4 m,设篮球运行轨迹为抛物线,篮圈距地面3 m.
(1)建立如图所示的平面直角坐标系,问此球能否准确投中?
(2)此时,对方队员乙在甲面前1 m处跳起盖帽拦截,已知乙的最大摸高为3.1 m,那么他能否获得成功?
例8.某乒乓球馆使用发球机进行辅助训练,出球口在桌面中线端点A处的正上方,如果每次发出的乒乓球的运动路线固定不变,且落在中线上,在乒乓球从发射出到第一次落在桌面的运行过程中,设乒乓球与端点A的水平距离为x(米),距桌面的高度为y(米),运行时间为t(秒),经多次测试后,得到如下部分数据:
t(秒) 0 0.16 0.2 0.4 0.6 0.64 0.8 …
x(米) 0 0.4 0.5 1 1.5 1.6 2 …
y(米) 0.25 0.378 0.4 0.45 0.4 0.378 0.25 …
(1)如果y是t的函数,
①如图,在平面直角坐标系tOy中,描出了上表中y与t各对对应值为坐标的点.请你根据描出的点,画出该函数的图象;
②当t为何值时,乒乓球达到最大高度?
(2)如果y是关于x的二次函数,那么乒乓球第一次落在桌面时,与端点A的水平距离是多少?
喷水问题
例9.如图,池中心竖直水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心3m,水管的长为_____.
例10. 某建筑物,从10m高的窗口A,用水管向外喷水,喷出的水呈抛物线状(抛物线所在的平面与墙面垂直),如图所示,如果抛物线的最高点M离墙1m,离地面m,则水流落地点B离墙的距离OB是( )
A.2m B.3m C.4m D.5m
例11.某小区有一半径为8m的圆形喷水池,喷水池的周边有一圈喷水头,喷出的水柱为抛物线.在距水池中心3m处达到最高,高度为5m,且各个方向喷出的水柱恰好在喷水池中心的装饰物处汇合.以水平方向为x轴,喷水池中心为原点建立如图所示的平面直角坐标系.
(1)求水柱所在抛物线对应的函数关系式;
(2)王师傅在喷水池维修设备期间,喷水管意外喷水,为了不被淋湿,身高1.8m的王师傅站立时必须在离水池中心多少米以内?
拱桥问题
例12 有一座抛物线形拱桥,正常水位桥下面宽度为米,拱顶距离水平面米,如图建立直角坐标系,若正常水位时,桥下水深米,为保证过往船只顺利航行,桥下水面宽度不得小于米,则当水深超过多少米时,就会影响过往船只的顺利航行( )
A. B. C. D.
例13.如图是抛物线型拱桥,当拱顶离水面2m时,水面宽4m,水面下降2m,水面宽度增加______m.
例14.廊桥是我国古老的文化遗产如图,是某座抛物线型的廊桥示意图,已知抛物线的函数表达式为,为保护廊桥的安全,在该抛物线上距水面AB高为8米的点E,F处要安装两盏警示灯,则这两盏灯的水平距离EF是______米精确到1米
题型3 利用函数思想解决几何问题中的最值问题
例15.如图,某小区计划在一块长为32m,宽为20m的矩形空地上修建三条同样宽的道路,剩余的空地上种植草坪,使草坪的面积为570m2.若设道路的宽为xm,则下面所列方程正确的是( )
A.(32﹣2x)(20﹣x)=570 B.32x+2×20x=32×20﹣570
C.(32﹣x)(20﹣x)=32×20﹣570 D.32x+2×20x﹣2x2=570
例16.如图,用长为6m的铝合金条制成“日”字形窗框,若窗框的宽为xm,窗户的透光面积为ym2(铝合金条的宽度不计).
(1)求出y与x的函数关系式;
(2)如何安排窗框的长和宽,才能使得窗户的透光面积最大?并求出此时的最大面积.
例17.如图,有长为的篱笆,一面利用墙(墙的最大长为),围成中间隔有一道篱笆的矩形花圃,设花圃的宽为,面积为.
(1)求与的函数解析式并求出的取值范围.
(2)当为多少时,矩形花圃面积最大,并求出最大值.
如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始沿边AB向B以2mm/s的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以4mm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,设运动的时间为ts,四边形APQC的面积为ymm2.
(1)y与t之间的函数关系式;
(2)求自变量t的取值范围;
(3)四边形APQC的面积能否等于172mm2.若能,求出运动的时间;若不能,说明理由.
题型4 增长率问题
某楼盘准备以每平方米16000元的均价对外销售,由于受有关房地产的新政策影响,购房者持币观望.开发商为促进销售,对价格进行了连续两次下调,结果以每平方米14440元的均价开盘销售,则平均每次下调的百分率为( )
A.5% B.8% C.10% D.11%
例20.某工厂2015年产品的产量为100吨,该产品产量的年平均增长率为x(x>0),设2017年该产品的产量为y吨,则y关于x的函数关系式为( )
A.y=100(1﹣x)2
B.y=100(1+x)2
C.y=
D.y=100+100(1+x)+100(1+x)2
例21.小红把班级勤工助学挣得的班费500元按一年期存入银行,已知年利率为x,一年到期后银行将本金和利息自动按一年定期转存,设两年到期后,本、利和为y元,则y与x之间的函数关系式为( )
A.y=500(x+1)2 B.y=x2+500 C.y=x2+500x D.y=x2+5x
例22.据农业农村部新闻部办公室2018年10月15日消息,江宁省发现疑似非洲猪瘟疫情,此次猪瘟疫情发病急,蔓延速度快.当政府和企业迅速进行了猪瘟疫情排查和处置,在疫情排查过程中,某农场第一天发现3头生猪发病,两天后发现共有192头生猪发病,
(1)求每头发病生猪平均每天传染多少头生猪
(2)若疫情得不到有效控制,3天后生猪发病头数会超过1500头吗
第一节:二次函数的定义
定义:一般地,形如(a,b,c是常数,a≠0)的函数,叫做二次函数.其中,x是自变量,a,b,c分别是函数解析式的二次项系数、一次项系数和常数项.
例1 当m 取何值时,函数是关于x 的二次函数?并求出这时二次函数的解析式.
题型1 二次函数的定义
1.下列函数是二次函数的是( )
A.y=x(x+1) B.x2y=1 C.y=2x3﹣2(x﹣1)2 D.y=x﹣0.5
2.下列函数中是二次函数的是( )
A. B. C. D.
3.下列函数中,一定是二次函数的是( )
A. B. C. D.
4.若y=(2-m)是二次函数,则m等于( )
A.±2 B.2 C.-2 D.不能确定
4.已知函数y=(k+2)是关于x的二次函数,则k=________.
5.若是二次函数,则m的值为________.
6. 已知函数
(1)当m为何值时,此函数为二次函数
(2)当m为何值时,此函数为一次函数
题型2 二次函数的一般式及函数值
二次函数的二次项系数为 ,一次项系数为 ,常数项为 。
把下列二次函数化为一般形式,并指出其二次项、一次项系数及常数项
(2)
(4)
题型3 利用二次函数模型解决实际问题
9.如图,在中,,,点从点沿边、匀速运动到点,过点作交于点,线段,,,则能够反映与之间函数关系的图象大致是( )
A. B.C.D.
第二节:二次函数的函数图象和性质
1、二次函数(a ≠ 0)的图象与性质
例1 如图, 四个二次函数的图象分别对应① ;② ;③ ;④ ,且①与③,②与④分别关于x 轴对称.
(1)比较a,b,c,d 的大小;
(2)说明a 与c,b 与d 的数量关系.
题型1 二次函数的函数图象
1.抛物线y=x2,y=﹣3x2,y=﹣x2,y=2x2的图象开口最大的是( )
A.y=x2 B.y=﹣3x2 C.y=﹣x2 D.y=2x2
2.在同一直角坐标系中,二次函数、、的图像的共同点是( )
A.关于y轴对称,开口向上
B.关于y轴对称,当x<0时,y随x 的增大而减小
C.关于y轴对称,最高点是原点
D.关于y轴对称,顶点坐标是(0,0)
3.函数y=ax-2 (a≠0).与y=ax2(a≠0)在同一平面直角坐标系中的图象可能是
A. B. C. D.
4.已知 a≠0,在同一坐标系中,y=ax与y=ax2的图象有可能是( )
A. B. C. D.
5.如图所示四个二次函数的图象中,分别对应的是①y=ax2;②y=bx2;③y=cx2;④y=dx2.则a、b、c、d的大小关系为_____.
6.如图,⊙O的半径为2,C1是函数y=x2的图象,C2是函数y=-x2的图象,则阴影部分的面积是________.
7.如图,垂直于x轴的直线AB分别与抛物线C1:y=x2(x≥0)和抛物线C2:y=(x≥0)交于A,B两点,过点A作CD∥x轴分别与y轴和抛物线C2交于点C、D,过点B作EF∥x轴分别与y轴和抛物线C1交于点E、F,则 的值为_____.
题型2 求待定系数问题
8.若抛物线y=ax2经过点A (,-9),则其解析式为_______________.
9.已知二次函数,如果当x=-1时y=2,那么当x=2时,y=_____.
10.二次函数有最低点,则m=__________
题型3 比较函数值大小
11.已知点(-2,),(0,),(1,)都在函数的图象上,则( )
A.>> B.>>
C.>> D.>>
12.已知a<-1,点(a-1,y1),(a,y2),(a+1,y3)都在函数y=x2的图象上,则( )
A.y1
题型4 利用函数性质解决问题
14.函数的部分对应值如下表:
… 0 1 2 …
… 2 0 2 …
根据表格回答:
(1)_________, ________;
(2)函数的解析式为 _________,定义域是 ________;
(3)请再举一些对应值,猜测该函数的图像关于________轴对称.
15. 已知函数是关于x 的二次函数.
(1)求满足条件的m 的值.
(2)当m 为何值时,其图象有最低点?求出这个最低点的坐标,这时当x 为何值时,y 随x 的增大而增大?
(3)当m 为何值时,函数有最大值?最大值是多少?这时当x为何值时,y 随x 的增大而减小?
16. 如图,已知函数与的交点为A,B(A在B的右边).
(1)求点A、点B的坐标; (2)连接,,求的面积.
第三节:二次函数的函数图象和性质
1、二次函数 的图象与二次函数 的图象的关系它们的形状(开口大小、方向)相同,只是上、下位置不同,二次函数的图象可由二次函数的图象上下平移|k| 个单位长度得到.
题型1 二次函数的图像及性质
1.抛物线y=x2+1的图象大致是( )
A. B. C. D.
2.二次函数y=-x2-1的图象大致是( )
A. B. C. D.
3.在同一坐标中,一次函数y=﹣kx+2与二次函数y=x2+k的图象可能是( )
A. B. C. D.
4.抛物线 的顶点坐标为(0,1),则抛物线的解析式为( )
A. B. C. D.
5.函数y=x2-4的图象与y轴的交点坐标是( )
A.(2,0) B.(-2,0) C.(0,4) D.(0,-4)
6.二次函数图像的对称轴是( ).
A.直线x=0 B.直线x=2 C.直线x=4 D.直线x= 4
7.点均在抛物线上,下列说法正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
8.下列点中,一定在二次函数y=x2﹣1图象上的是( )
A.(0,0) B.(1,1) C.(1,0) D.(0,1)
9.若二次函数的图像经过点、,则、的大小关系是( )
A. B. C. D.不能确定
10.二次函数y=﹣2x2﹣1图象的顶点坐标为( )
A.(0,0) B.(0,﹣1) C.(﹣2,﹣1) D.(﹣2,1)
11. 如图抛物线经过正方形OBAC的顶点A,B,C,则c= .
12. 已知抛物线具有如下性质:该抛物线上任意一点到定点的距离与到x轴的距离始终相等。如图,点M的坐标为,P是抛物线上的一个动点,则周长的最小值是 。
题型2 二次函数与二次函数的
13.二次函数y=x2的图象向上平移3个单位,得到新的图象的二次函数表达式是( ).
A. B. C. D.
14. 能否通过上下平移二次函数的图像,使得新得到的函数图像过点(3,-3)?若能,说出平移的方向和距离;若不能,说明理由。
15. 已知抛物线,当1≤x ≤5时,y的最大值是________ .
16. 已知抛物线,当时,y的最大值是 .
17. 已知:抛物线与直线交于点(m,3).
(1)求m和n的值;
(2)试说出抛物线的顶点坐标和对称轴;
(3)当x何值时,二次函数中y随x的增大而减小;
(4)函数与的图象是否还存在其它交点,若存在,请求出交点坐标;若没有,请说明理由.
第四节:二次函数的函数图象和性质
1. 二次函数的图象与二次函数 的图象的关系它们的形状(开口大小、方向)相同,只是左、右位置不同,二次函数 的图象可由二次函数的图象左右平移|h| 个单位长度得到.
题型1 二次函数的函数图象和性质
1.抛物线顶点坐标是
A. B. C. D.
2.在一次函数y=kx+b(k≠0)中,y随x的增大而减小,则二次函数y=k(x﹣1)2的图象大致是( )
A. B. C. D.
3.已知A(-4,y1),B(-3,y2),C(3,y3)三点都在二次函数y=-2(x+2)2的图象上,则y1,y2,y3的大小关系为___.
4. 已知A(,y1),B(1,y2),C(4,y3)三点都在二次函数y=﹣(x﹣2)2的图象上,则y1,y2,y3的大小关系为( )
A.y1<y2<y3 B.y1<y3<y2 C.y3<y1<y2 D.y3<y2<y1
题型2 二次函数与之间的关系
5.函数的图象可以由函数的图象( )得到
A.向左平移3个单位 B.向右平移3个单位
C.向上平移3个单位 D.向下平移3个单位
6. 抛物线向左平移3个单位长度,所得到的抛物线所对应的函数解析式为( )
7. 如图,坐标平面内有一顶点为A的抛物线,此抛物线与直线交于B,C两点,为正三角形,若A点的坐标为(-3,0),则此抛物线与y轴的交点坐标是 。
8.如图,Rt△OAB中,∠OAB=90°,O为坐标原点,边OA在x轴上,OA=AB=1个单位长度.把Rt△OAB沿x轴正方向平移1个单位长度后得△AA1B.
(1)求以A为顶点,且经过点B1的抛物线的解析式;
(2)若(1)中的抛物线与OB交于点C,与y轴交于点D,求点D、C的坐标.
第五节:二次函数的函数图象和性质
题型1 二次函数的函数图象和性质
1.二次函数y=﹣(x-2)2+1的图象中,若y随x的增大而减小,则x的取值范围是( )
A.x<2 B.x>2 C.x<﹣2 D.x>﹣2
2.二次函数 y=(x﹣2)2+3,当 0≤x≤5 时,y 的取值范围为( )
A.3≤y≤12 B.2≤y≤12 C.7≤y≤12 D.3≤y≤7
3.如果点是抛物线上两个不同的点,那么的值为( )
A.4 B.5 C.6 D.7
4.对于抛物线y=﹣(x+2)2+3,下列结论中正确结论的个数为( )
①抛物线的开口向下; ②对称轴是直线x=﹣2;
③图象不经过第一象限; ④当x>2时,y随x的增大而减小.
A.4 B.3 C.2 D.1
5.二次函数,当时,y随x的增大而增大,则m的取值范围是_____________
6.若二次函数y=a(x+h)2+k的图象经过(-3,0),(5,0)两点,则h的值为________
题型2 二次函数的平移
将抛物线向右平移2个单位长度,再向上平移1个单位长度,所得抛物线对应的函数解析式为( )
8. 不论取任何实数,抛物线的顶点都( ).
在直线上 B.在直线上
C.在直线上 D.不确定
9. 已知二次函数y=(x-2a)2+(a-1)(a为常数),当a取不同的值时,其图象构成一个“抛物线系”.如图分别是当a=-1,a=0,a=1,a=2时二次函数的图象.它们的顶点在一条直线上,这条直线的解析式是____________________.
10.如图,在平面直角坐标系中,O是坐标原点,点A的坐标是,过点A作轴,垂足为B,连接,抛物线经过点A,与x轴正半轴交于点C.
(1)求c的值;
(2)将抛物线向下平移m个单位,使平移后得到的抛物线顶点落在的内部(不包括的边界),求m的取值范围.
题型3 函数值大小比较
11.已知点A(x1,y1),B(x2,y2)在二次函数y=(x-1)2+1的图象上.若x1>x2>1,则y1________y2(填“>”“<”或“=”).
12.已知点A(4,y1),B(,y2),C(-2,y3)都在二次函数y=(x-2)2-1的图象上,则y1,y2,y3的大小关系是 .
13. 如图,抛物线与轴交于,两点在的左侧),与轴交于点,点与关于抛物线的对称轴对称.
(1)求抛物线的解析式及点的坐标;
(2)点是抛物线上的一点,当的面积是8,求出点的坐标;
(3)过直线下方的抛物线上一点作轴的平行线,与直线交于点,已知点的横坐标是,试用含的式子表示的长及△ADM的面积,并求当的长最大时的值.
第六节:二次函数的函数图象和性质
二次函数的各项系数的符号与图象位置间的关系:
(1)a决定抛物线的开口方向,简记为“正上负下”;
(2)c决定抛物线与y轴的交点位置,简记为“上正下负原点0”;
(3)a、b的符号共同决定对称轴x=的位置,简记为:“左同右异y轴0”;可以由各项系数的符号来决定图象的位置,也可以由图象的位置来判断各项系数的符号.
题型1 二次函数的函数图象和性质
1.抛物线的顶点坐标是( )
A. B. C. D.
2.二次函数的顶点和对称轴分别是 ( )
A.,直线x=1 B.,直线x=4
C.,直线 D.,直线
3.若二次函数的图像对称轴为直线经过不同的5点,,,,,则,,的大小关系( )
A. B. C. D.
4.点P(m,n)在以y轴为对称轴的二次函数y=x2+ax+4的图象上.则m﹣n的最大值等于( )
A. B.4 C.﹣ D.﹣
5.已知关于x的二次函数y=x2+(2-a)x+5,当1≤x≤3时,y在x=1时取得最大值,则实数a的取值范围是( )
A.a≥2 B.a≤-2 C.a≥6 D.a<0
题型2 二次函数与二次函数之间的转换
6.二次函数图象的顶点坐标是 .
7.已知抛物线的顶点坐标为(3,-1),则b=_____,c=______.
8.指出下列函数的开口方向、对称轴、顶点坐标和变化情况
(1)
(2)
9.已知二次函数的图像过抛物线的顶点和坐标原点.
(1)求二次函数的解析式
(2)判断点A(-2,5)是否在这个二次函数的图像上 .
10.抛物线y=﹣x2+(m-1)x+m与y轴交于(0,3)点,
(1)求m的值;
(2)当x取何值时,抛物线在x轴的上方.
题型3 二次函数的图像与之间的关系
11.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①a+b+c<0;②b2﹣4ac>0;③b>0;④4a﹣2b+c<0;⑤a+c<,其中正确结论的个数是( )
A.②③④ B.①②⑤ C.①②④ D.②③⑤
12.已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论中正确的是( )
A.abc>0 B.b2﹣4ac<0 C.9a+3b+c>0 D.c+8a<0
13.如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,直线x=-1是对称轴,有下列判断:①b-2a=0;②4a-2b+c<0;③a-b+c=-9a;④若(-3,y1),(,y2)是抛物线上两点,则y1>y2,其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
专题1 二次函数解析式的求法
待定系数法求二次函数解析式
用一般式(三点式)确定二次函数解析式
1.已知二次函数图像经过下列点,求二次函数的解析式:
(1)(0,-1),(1,-1),(2,3)
(2)(0,0),(2,0),(-3,3)
2.已知二次函数图像经过下列点,求二次函数的解析式:
(1)(0,-1),(1,-1),(2,3)
(2)(0,0),(2,0),(-3,3)
用顶点式确定二次函数解析式
若抛物线的顶点是,且经过,则抛物线的函数解析式为
二次函数的图象的顶点在坐标轴上,则的值为__________.
5.已知抛物线顶点为(2,3),且经过(1,2)求二次函数解析式.
用交点式确定二次函数解析式
抛物线与x轴交与,B(- 3,0)两点,求该抛物线的解析式
利用对称确定二次函数解析式
已知抛物线的对称轴为直线并且与x轴的一个交点为(3,0),那么它所对应的函数解析式是 。
利用平移求二次函数解析式
7.将抛物线的图象绕着顶点旋转后得到的抛物线是_____________
8.将抛物线绕顶点旋转,则旋转后的抛物线的解析式为( )
A. B.
C. D.
9.将抛物线的图象绕原点旋转,则旋转后的抛物线的函数关系式( )
A. B. C. D.
10.二次函数的图像以x轴为对称轴翻折,翻折后它的函数解析式是_____.
利用直线与二次函数交点求解解析式
11.二次函数与直线的图象交于点
求,的值;
写出二次函数的表达式,并指出取何值时该表达式随的增大而增大?
写出该抛物线的顶点坐标和对称轴
12.如图,抛物线y=ax2+bx过点P(﹣1,5),A(4,0).
(1)求抛物线的解析式;
(2)在第一象限内的抛物线上有一点B,当PA⊥PB时,求点B的坐标.
13.一次函数与二次函数的图象的一个交点坐标是,另一个交点是该二次函数图象的顶点.
(1)求k,a,c的值.
(2)过点A(0,m)(0
14.下表是二次函数y=ax2+bx+c的x,y的部分对应值:
x … 0 1 2 …
y … ﹣1 m ﹣1 n …
则对于该函数的性质的判断:①该二次函数有最大值;②不等式y>﹣1的解集是x<0或x>2;③方程ax2+bx+c=0的两个实数根分别位于﹣<x<0和2<x<之间;④当x>0时,函数值y随x的增大而增大;其中正确的是( )
A.②③ B.②④ C.①③ D.③④
15.二次函数(a,b,c为常数且a≠0)中的与的部分对应值如下表:
0 1 3
3 5 3
现给出如下四个结论:①;② 当时,的值随值的增大而减小;③是方程的一个根;④当时,,其中正确结论的序号为:__ __.
16.已知二次函数y=ax2+bx+c(a≠0)中,函数值y与自变量x的部分对应值如表:
x … ﹣5 ﹣4 ﹣3 ﹣2 ﹣1 …
y … 3 ﹣2 ﹣5 ﹣6 ﹣5 …
则关于x的一元二次方程ax2+bx+c=3的根是_____.
17.已知二次函数y=ax2+bx+c(a≠0)自变量x的值和它对应的函数值y如表所示:
(1)请写出该二次函数图象的开口方向、对称轴、顶点坐标和m的值;
(2)设该二次函数图象与x轴的左交点为B,它的顶点为A,该图象上点C的横坐标为4,求△ABC的面积.
18.根据学习函数的经验,探究函数y=x2+ax﹣4|x+b|+4(b<0)的图象和性质:
(1)下表给出了部分x,y的取值;
x L ﹣3 ﹣2 ﹣1 0 1 2 3 4 5 L
y L 3 0 ﹣1 0 3 0 ﹣1 0 3 L
由上表可知,a= ,b= ;
(2)用你喜欢的方式在坐标系中画出函数y=x2+ax﹣4|x+b|+4的图象;
(3)结合你所画的函数图象,写出该函数的一条性质;
(4)若方程x2+ax﹣4|x+b|+4=x+m至少有3个不同的实数解,请直接写出m的取值范围.
几何应用中求二次函数解析式
19. 已知,如图抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
(1)求抛物线的解析式;
20. 如图,抛物线交X轴于A、B两点,交Y轴于点C ,,求抛物线的解析式;
专题2 二次函数图像与系数之间的关系
1.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①3a+b<0;②a﹣b+c<0;③c>0;④a+b>0.其中正确的结论有( )
A.仅①②③ B.仅②③④
C.仅①②④ D.①②③④
2.二次函数y=ax2+bx+c的图象如图所示,则下列命题中:①b=﹣2a;②此抛物线向下移动c个单位后过点(2,0);③﹣1<a<﹣;④方程x2﹣2x+=0有实数根,结论正确的个数( )
A.1个 B.2个 C.3个 D.4个
3.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:
①abc>0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤a+b>m(am+b)(m≠1的实数).
其中正确的结论有( )
A.2个 B.3个 C.4个 D.5个
4.在同一直角坐标系中,函数和函数(m是常数,且)的图象可能是( )
A.B.C. D.
5.已知是非零实数,,在同一平面直角坐标系中,二次函数与一次函数的大致图象不可能是( )
A. B. C. D.
专题3 二次函数与一元二次方程和不等式之间的关系
二次函数与一元二次方程之间的关系
1.已知二次函数(m为常数)的图象与x轴的一个交点为,则关于x的一元二次方程的两实数根分别是( )
A. B. C. D.
2.若抛物线经过第四象限的点),则关于x的方程的根的情况是( )
A.有两个大于1的不相等实数根 B.有两个小于1的不相等实数根
C.有一个大于1另一个小于1的实数根 D.没有实数根
3.抛物线与x轴只有一个公共点,则m的值为________.
4.抛物线经过、两点,若关于的一元二次方程的一个解为,则__________.
5.已知关于x的一元二次方程有两个不相等的实数根.
(1)求k的取值范围;
(2)若k取小于1的整数,且此方程的解为整数,则求出此方程的两个整数根;
(3)在(2)的条件下,二次函数与x轴交于A、B两点(A点在B点的左侧),D点在此抛物线的对称轴上,若∠DAB=60 ,直接写出D点的坐标.
二次函数与不等式之间的关系
6.抛物线的部分图象如图所示,若,则的取值范围是( )
B.或 C.或 D.
7.如图,一次函数y1=kx+n(k≠0)与二次函数y2=ax2+bx+c(a≠0)的图象相交于A(﹣1,5)、B(9,2)两点,则关于x的不等式kx+n≥ax2+bx+c的解集为( )
A.﹣1≤x≤9 B.﹣1≤x<9 C.﹣1<x≤9 D.x≤﹣1或x≥9
8.如图,抛物线和直线,当时,的取值范围是( )
B.或 C.或 D.
9.抛物线y=﹣x2+bx+c的部分图象如图所示,若y>0,则x的取值范围是_____.
10.如图,二次函数的图象的顶点C的坐标为,与x轴交于,根据图象回答下列问题:
(1)写出方程的根;
(2)写出不等式的解集.
专题4 二次函数与几何结合问题
二次函数中的距离最值问题
1. P是抛物线上一点,过点P作PM⊥x轴,PN⊥y轴,垂足分别是M,N,则PM+PN的最小值是( )
A. B. C.3 D.5
2.如图,抛物线与x轴交于A,B两点,其中点A的坐标为,与y轴交于点C,点在抛物线上.
(1)求抛物线的解析式;
(2)抛物线的对称轴上有一动点P,求出的最小值;
(3)若抛物线上有一动点Q,使的面积为6,求点Q的坐标.
3.如图,在平面直角坐标系上,一条抛物线y=ax2+bx+c(a≠0)经过A(1,0)、B(3,0)、C(0,3)三点,连接BC并延长.
(1)求抛物线的解析式;
(2)点M是直线BC在第一象限部分上的一个动点,过M作MN∥y轴交抛物线于点N.
①求线段MN的最大值;
②当MN取最大值时,在线段MN右侧的抛物线上有一个动点P,连接PM、PN,当△PMN的外接圆圆心Q在△PMN的边上时,求点P的坐标.
二次函数中几何面积/周长最值问题
4.已知二次函数的图象以(-1,4)为顶点,且过点(2,-5),x轴交点为A,B,(A在B左侧).与y轴交于点C,
(1)求该函数的关系式;
(2)求△ABC的面积.
(3)若在抛物线上有一点M,使△ABM的面积是△ABC的面积的2倍,求M点坐标.
5.如图,抛物线y=ax2+bx+3(a≠0)的对称轴为直线x=﹣1,抛物线交x轴于A、C两点,与直线y=x﹣1交于A、B两点,直线AB与抛物线的对称轴交于点E.
(1)求抛物线的解析式.
(2)点P在直线AB上方的抛物线上运动,若△ABP的面积最大,求此时点P的坐标.
(3)在平面直角坐标系中,以点B、E、C、D为顶点的四边形是平行四边形,请直接写出符合条件点D的坐标.
6.如图1,抛物线与轴交于点,对称轴与抛物线交于点,与轴交于点.
(1)求抛物线的解析式.
(2)点是轴上的动点,求的最小周长.
(3)如图2,点是抛物线上一个动点,分别与交于点.
①若动点在第一象限,问的值是否发生变化.若不变,求出其值;若发生变化,请说明理由.
②若动点在第二象限,请给出①中类似的关于与长的结论(不必证明).
二次函数中的存在问题
7.直线与x轴y轴分别交于点A,B,抛物线经过点A,B,并与x轴交于另一点C,其顶点为P,
(1)求的值;
(2)抛物线的对称轴上有一点Q,使是以AB为底边的等腰三角形,求点Q的坐标;
8.如图,抛物线与x轴交于A(-1,0),B(5 ,0)两点,直线与y轴交于点C,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m.
(1)求抛物线的解析式;
(2)若PE=3+4EF,求m的值;
(3)是否存在点P,使得△PCE与△DEF相似.若存在,求出点P的坐标,若不存在,请说明理由.
9.如图,抛物线y=ax2+bx+c(a≠0)的图象经过A(1,0),B(3,0),C(0,6)三点.
(1)求抛物线的解析式.
(2)抛物线的顶点M与对称轴l上的点N关于x轴对称,直线AN交抛物线于点D,直线BE交AD于点E,若直线BE将△ABD的面积分为1:2两部分,求点E的坐标.
(3)P为抛物线上的一动点,Q为对称轴上动点,抛物线上是否存在一点P,使A、D、P、Q为顶点的四边形为平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
10.综合与探究
如图,抛物线经过点A(-2,0),B(4,0)两点,与轴交于点C,点D是抛物线上一个动点,设点D的横坐标为.连接AC,BC,DB,DC,
(1)求抛物线的函数表达式;
(2)△BCD的面积等于△AOC的面积的时,求的值;
(3)在(2)的条件下,若点M是轴上的一个动点,点N是抛物线上一动点,试判断是否存在这样的点M,使得以点B,D,M,N为顶点的四边形是平行四边形,若存在,请直接写出点M的坐标;若不存在,请说明理由.
利用直线平移与二次函数图像交点情况求字母取值范围
【中考.菏泽】如图,在平面直角坐标系中,抛物线过,两点。
求抛物线的解析式;
记抛物线顶点为D,求的面积;
若直线向上平移c个单位所得直线与抛物线段BCD(包括两个端点B,C)部分有两个交点,求c的取值范围。
专题5二次函数实际问题
题型1 利用二次函数解决销售利润中的最值问题
求最大利润问题
例1.某超市购进一批成本为每件元的商品,经调查发现,该商品每天的销售量(件)与销售单价(元)之间满足一次函数关系,其图象如图所示.
(1)求该商品每天的销售量与销售单价之间的函数关系式;
(2)若超市按单价不低于成本价,且不高于元销售,则销售单价定为多少,才能使销售该商品每天获得的利润(元)最大
(3)若超市要使销售该商品每天获得的利润为元,则每天的销售量应为多少件
例2.某商店销售一种销售成本为40元/千克的水产品,若按50元/千克销售,一个月可售出500千克,销售价每涨价1元,月销售量就减少10千克.
(1)写出月销售利润(单位:元)与售价(单位:元/千克)之间的函数关系式.
(2)商场将在月销售成本不超过3000元的情况下,使得月销售利润达到8000元,销售单价应定为多少?
(3)当售价定为多少元时,会获得最大利润?求出最大利润.
例3.某超市销售一种文具,进价为5元/件.售价为6元/件时,当天的销售量为100件.在销售过程中发现:售价每上涨0.5元,当天的销售量就减少5件.设当天销售单价统一为元/件(,且是按0.5元的倍数上涨),当天销售利润为元.
(1)求与的函数关系式(不要求写出自变量的取值范围);
(2)要使当天销售利润不低于240元,求当天销售单价所在的范围;
(3)若每件文具的利润不超过,要想当天获得利润最大,每件文具售价为多少元?并求出最大利润.
例4.某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,经试销发现,销售量(件)与销售单价(元)符合一次函数,且时,;时,.
(1)求一次函数的表达式;
(2)若该商场获得利润为元,试写出利润与销售单价之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
(3)若该商场获得利润不低于500元,试确定销售单价的范围.
优选销售方案
例5.某商场要经营一种新上市的文具,进价为20元,试营销阶段发现:当销售单价是25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件
(1)写出商场销售这种文具,每天所得的销售利润(元)与销售单价(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大;
(3)商场的营销部结合上述情况,提出了A、B两种营销方案
方案A:该文具的销售单价高于进价且不超过30元;
方案B:每天销售量不少于10件,且每件文具的利润至少为25元
请比较哪种方案的最大利润更高,并说明理由
例6.浩然文具店新到一种计算器,进价为25元,营销时发现:当销售单价定为30元时,每天的销售量为150件,若销售单价每上涨1元,每天的销售量就会减少10件.
(1)写出商店销售这种计算器,每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式;
(2)求销售单价定为多少元时,每天的销售利润最大?最大值是多少?
(3)商店的营销部结合上述情况,提出了A、B两种营销方案:
方案A:为了让利学生,该计算器的销售利润不超过进价的24%;
方案B:为了满足市场需要,每天的销售量不少于120件.
请比较哪种方案的最大利润更高,并说明理由.
题型2 利用建立二次函数模型解决实际中抛物线型最值问题
投球问题
例7.在一次篮球比赛中,如图队员甲正在投篮.已知球出手时离地面m,与篮圈中心的水平距离为7 m,球出手后水平距离为4 m时达到最大高度4 m,设篮球运行轨迹为抛物线,篮圈距地面3 m.
(1)建立如图所示的平面直角坐标系,问此球能否准确投中?
(2)此时,对方队员乙在甲面前1 m处跳起盖帽拦截,已知乙的最大摸高为3.1 m,那么他能否获得成功?
例8.某乒乓球馆使用发球机进行辅助训练,出球口在桌面中线端点A处的正上方,如果每次发出的乒乓球的运动路线固定不变,且落在中线上,在乒乓球从发射出到第一次落在桌面的运行过程中,设乒乓球与端点A的水平距离为x(米),距桌面的高度为y(米),运行时间为t(秒),经多次测试后,得到如下部分数据:
t(秒) 0 0.16 0.2 0.4 0.6 0.64 0.8 …
x(米) 0 0.4 0.5 1 1.5 1.6 2 …
y(米) 0.25 0.378 0.4 0.45 0.4 0.378 0.25 …
(1)如果y是t的函数,
①如图,在平面直角坐标系tOy中,描出了上表中y与t各对对应值为坐标的点.请你根据描出的点,画出该函数的图象;
②当t为何值时,乒乓球达到最大高度?
(2)如果y是关于x的二次函数,那么乒乓球第一次落在桌面时,与端点A的水平距离是多少?
喷水问题
例9.如图,池中心竖直水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心3m,水管的长为_____.
例10. 某建筑物,从10m高的窗口A,用水管向外喷水,喷出的水呈抛物线状(抛物线所在的平面与墙面垂直),如图所示,如果抛物线的最高点M离墙1m,离地面m,则水流落地点B离墙的距离OB是( )
A.2m B.3m C.4m D.5m
例11.某小区有一半径为8m的圆形喷水池,喷水池的周边有一圈喷水头,喷出的水柱为抛物线.在距水池中心3m处达到最高,高度为5m,且各个方向喷出的水柱恰好在喷水池中心的装饰物处汇合.以水平方向为x轴,喷水池中心为原点建立如图所示的平面直角坐标系.
(1)求水柱所在抛物线对应的函数关系式;
(2)王师傅在喷水池维修设备期间,喷水管意外喷水,为了不被淋湿,身高1.8m的王师傅站立时必须在离水池中心多少米以内?
拱桥问题
例12 有一座抛物线形拱桥,正常水位桥下面宽度为米,拱顶距离水平面米,如图建立直角坐标系,若正常水位时,桥下水深米,为保证过往船只顺利航行,桥下水面宽度不得小于米,则当水深超过多少米时,就会影响过往船只的顺利航行( )
A. B. C. D.
例13.如图是抛物线型拱桥,当拱顶离水面2m时,水面宽4m,水面下降2m,水面宽度增加______m.
例14.廊桥是我国古老的文化遗产如图,是某座抛物线型的廊桥示意图,已知抛物线的函数表达式为,为保护廊桥的安全,在该抛物线上距水面AB高为8米的点E,F处要安装两盏警示灯,则这两盏灯的水平距离EF是______米精确到1米
题型3 利用函数思想解决几何问题中的最值问题
例15.如图,某小区计划在一块长为32m,宽为20m的矩形空地上修建三条同样宽的道路,剩余的空地上种植草坪,使草坪的面积为570m2.若设道路的宽为xm,则下面所列方程正确的是( )
A.(32﹣2x)(20﹣x)=570 B.32x+2×20x=32×20﹣570
C.(32﹣x)(20﹣x)=32×20﹣570 D.32x+2×20x﹣2x2=570
例16.如图,用长为6m的铝合金条制成“日”字形窗框,若窗框的宽为xm,窗户的透光面积为ym2(铝合金条的宽度不计).
(1)求出y与x的函数关系式;
(2)如何安排窗框的长和宽,才能使得窗户的透光面积最大?并求出此时的最大面积.
例17.如图,有长为的篱笆,一面利用墙(墙的最大长为),围成中间隔有一道篱笆的矩形花圃,设花圃的宽为,面积为.
(1)求与的函数解析式并求出的取值范围.
(2)当为多少时,矩形花圃面积最大,并求出最大值.
如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始沿边AB向B以2mm/s的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以4mm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,设运动的时间为ts,四边形APQC的面积为ymm2.
(1)y与t之间的函数关系式;
(2)求自变量t的取值范围;
(3)四边形APQC的面积能否等于172mm2.若能,求出运动的时间;若不能,说明理由.
题型4 增长率问题
某楼盘准备以每平方米16000元的均价对外销售,由于受有关房地产的新政策影响,购房者持币观望.开发商为促进销售,对价格进行了连续两次下调,结果以每平方米14440元的均价开盘销售,则平均每次下调的百分率为( )
A.5% B.8% C.10% D.11%
例20.某工厂2015年产品的产量为100吨,该产品产量的年平均增长率为x(x>0),设2017年该产品的产量为y吨,则y关于x的函数关系式为( )
A.y=100(1﹣x)2
B.y=100(1+x)2
C.y=
D.y=100+100(1+x)+100(1+x)2
例21.小红把班级勤工助学挣得的班费500元按一年期存入银行,已知年利率为x,一年到期后银行将本金和利息自动按一年定期转存,设两年到期后,本、利和为y元,则y与x之间的函数关系式为( )
A.y=500(x+1)2 B.y=x2+500 C.y=x2+500x D.y=x2+5x
例22.据农业农村部新闻部办公室2018年10月15日消息,江宁省发现疑似非洲猪瘟疫情,此次猪瘟疫情发病急,蔓延速度快.当政府和企业迅速进行了猪瘟疫情排查和处置,在疫情排查过程中,某农场第一天发现3头生猪发病,两天后发现共有192头生猪发病,
(1)求每头发病生猪平均每天传染多少头生猪
(2)若疫情得不到有效控制,3天后生猪发病头数会超过1500头吗
同课章节目录
