广东省揭阳市2022届高三上学期期末考试数学试题(Word版含答案解析)
文档属性
| 名称 | 广东省揭阳市2022届高三上学期期末考试数学试题(Word版含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-18 12:12:01 | ||
图片预览




文档简介
☆开封前注意保密
揭阳市2022届高三上学期期末考试
数学
本试卷共4页,考试时间120分钟,满分150分
注意事项:
1.答题前,考生先将自已的信息填写清楚 准确,将条形码准确粘贴在条形码粘贴处.
2.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效.
3.答题时请按要求用笔,保持卡面清洁,不要折叠,不要弄破 弄波,不得使用涂改液 修正带 刮纸刀.考试结束后,请将本试卷及答题卡交回.
一 选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设集合,则( )
A. B.
C. D.
2.复数满足为虚数单位,则的模为( )
A. B. C.1 D.
3.袋中有大小和形状都相同的3个白球和2个黑球,现从袋中不放回地依次抽取两个球,则在第一次取到白球的条件下,第二次也取到白球的概率是( )
A. B. C. D.
4.每年的毕业季都是高校毕业生求职和公司招聘最忙碌的时候,甲 乙两家公司今年分别提供了2个和3个不同的职位,一共收到了100份简历,具体数据如下:
公司 文史男 文史女 理工男 理工女
甲 10 10 20 10
乙 15 20 10 5
分析毕业生的选择意愿与性别的关联关系时,已知对应的的观测值;分析毕业生的选择意愿与专业关联的的观测值,则下列说法正确的是( )
A.有的把握认为毕业生的选择意愿与专业相关联
B.毕业生在选择甲 乙公司时,选择意愿与专业的关联比与性别的关联性更大一些
C.理科专业的学生更倾向于选择乙公司
D.女性毕业生更倾向于选择甲公司
5.已知函数,则该函数的增区间为( )
A.
B.
C.
D.
6.已知圆柱的轴截面为正方形,其外接球为球,则圆柱的表面积与球的表面积之比为( )
A. B. C. D.不能确定
7.已知过抛物线的焦点的直线交于两点(点在点的右边),为原点.若的重心的横坐标为10,则的值为( )
A.144 B.72 C.60 D.48
8.已知函数,过点可作两条直线与函数相切,则下列结论正确的是( )
A. B.
C.的最大值为2 D.
二 多选题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.已知二项式的展开式中各项的系数和为64,则下列说法正确的是( )
A.展开式中的常数项为1
B.
C.展开式中二项式系数最大的项是第四项
D.展开式中的指数均为偶数
10.已知函数,实数满足不等式,则( )
A. B.
C. D.
11.已知向量,且,则下列说法正确的是( )
A. B.
C. D.的最大值为2
12.如图所示,已知正方体的棱长为分别是的中点,是线段上的动点,则下列说法正确的是( )
A.平面截正方体所得的截面可以是四边形 五边形或六边形
B.当点与两点不重合时,平面截正方体所得的截面是五边形
C.是锐角三角形
D.面积的最大值是
三 填空题:本题共4小题,每小题5分,共20分.
13.已知函数,该函数在处的切线方程为__________.
14.在等差数列中,分别是方程的两个根,则__________.
15.如图所示,已知是双曲线右支上任意一点,双曲线在点处的切线分别与两条渐近线交于两点,则__________.
16.如图所示,在等腰直角中,为的中点,,分别为线段上的动点,且.
(1)当时,则的值为__________.
(2)的最大值为__________.
四 解答题:本题共6小题,共70分.解答应写出文字说明 证明过程或演算步骤.
17.(10分)
在各项均为正数的等比数列中,.
(1)求数列的通项公式;
(2),求数列的前项和.
18.(12分)
在中,角所对的边分别为,且.
(1)求角;
(2)若,且的面积为,且,求和的值.
19.(12分)
如图,在四棱锥中,底面为梯形,,平面平面为棱上的点,且.
(1)求证:平面;
(2)若,二面角为,求直线与平面所成角的正弦值.
20.(12分)
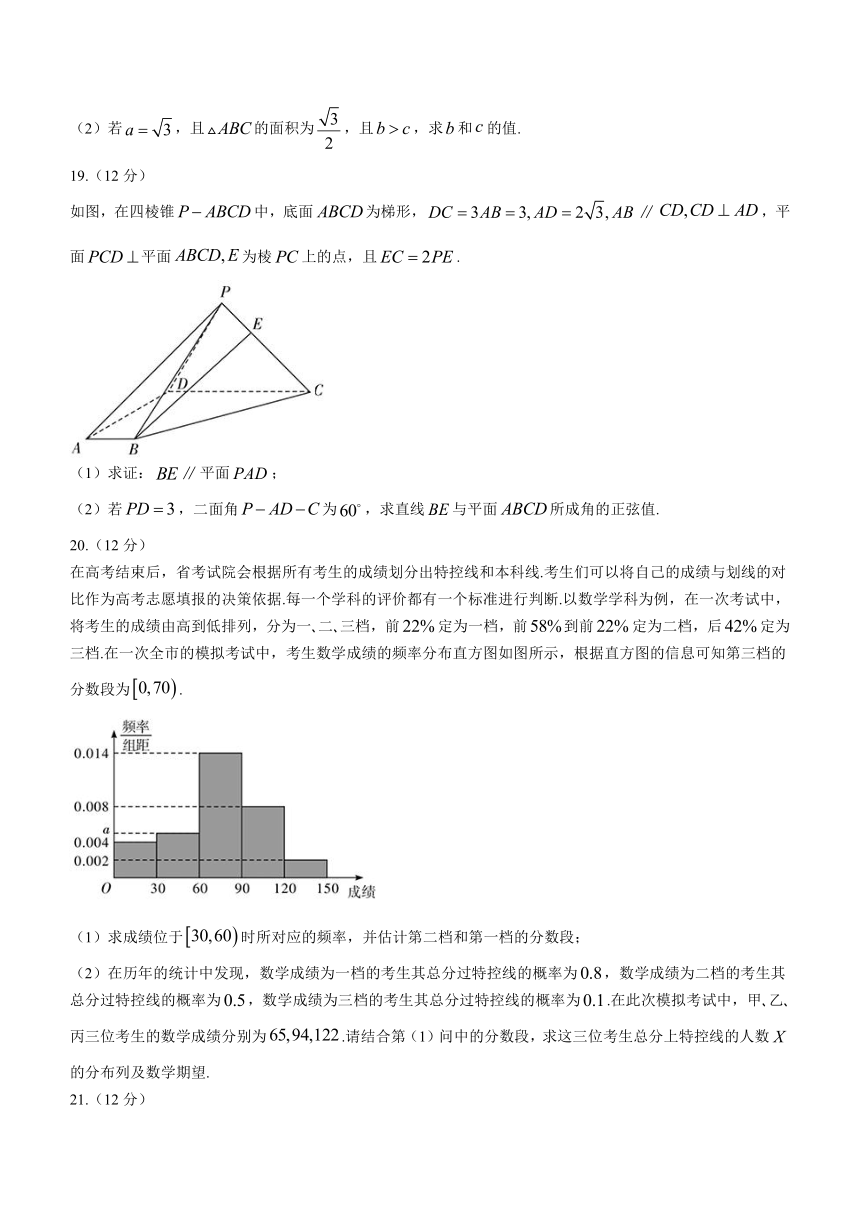
在高考结束后,省考试院会根据所有考生的成绩划分出特控线和本科线.考生们可以将自己的成绩与划线的对比作为高考志愿填报的决策依据.每一个学科的评价都有一个标准进行判断.以数学学科为例,在一次考试中,将考生的成绩由高到低排列,分为一 二 三档,前定为一档,前到前定为二档,后定为三档.在一次全市的模拟考试中,考生数学成绩的频率分布直方图如图所示,根据直方图的信息可知第三档的分数段为.
(1)求成绩位于时所对应的频率,并估计第二档和第一档的分数段;
(2)在历年的统计中发现,数学成绩为一档的考生其总分过特控线的概率为,数学成绩为二档的考生其总分过特控线的概率为,数学成绩为三档的考生其总分过特控线的概率为.在此次模拟考试中,甲 乙 丙三位考生的数学成绩分别为.请结合第(1)问中的分数段,求这三位考生总分上特控线的人数的分布列及数学期望.
21.(12分)
已知椭圆为椭圆的左 右焦点,焦距为,点在上,且面积的最大值为.
(1)求椭圆的方程;
(2)过点作直线交椭圆于两点,以为直径的圆是否恒过轴上的定点?若存在该定点,请求出的值;若不存在,请说明理由.
22.(12分)
已知函数
(1)若,判断函数的单调性,并求出函数的最值.
(2)若函数有两个零点,求实数的取值范围.
揭阳市2022届高三上学期期末考试
数学
试卷参考答案与评分标准
一 选择题:本题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1 2 3 4 5 6 7 8
D C C B C A D B
1.D 先将集合分别化简,再求其交集.,从而.
2.C 先做除法运算求出复数,再根据复数模的计算公式求其模.由得,从而
3.C 此题为条件概率模型,可以有两种做法:一是根据条件概率的公式计算;二是缩小样本空间的方法术解.
方法一:记第次取得白球为事件;
方法二:第一次取到白球后,袋中还有4个球,两白两黑,故第二次取出白球的概率为.
4.B 根据的观测值的意义再结合所给表格中的参考数据进行判断.与专业关联的的观测值,明显大于,明显小于,故仅有的把握认为毕业生的选择意原与专业相关联,所以不正确;因为,故正确;根据题中的数据表列出专业与甲 乙公司的关联表可知,理科专业的学生更倾向于选择甲公司,列出性别与甲 乙公司的关联表可知,女性毕业生更倾向于选择C公司,所以C,D均不对.
5.C 利用整体代换法和复合函数的单调性求函数的增区间.令,解得,故答案为C.
6.A 利用圆柱的轴截面信息求出圆柱的底面半径与高的关系,再结合圆柱与外接球的关系求得对应的比例关系.因为圆柱的轴截面为正方形,设圆柱底面圆的半径为,其高,其外接球的半径,则圆柱的表面积,球的表面积,则有,故答案为.
7.D 利用三角形的重心公式可得点的坐标所满足的关系,结合焦点弦长与点的坐标关系求得的值.抛物线的焦点,准线设点的坐标分别为,根据重心坐标公式得,可得.根据抛物线的几何性质,得,故答案为D.
8.B 根据函数的图像及其渐进线将平面直角坐标系划分为不同的区域,在不同区域内的点作函数的切线的条数不同.由此获得点所在的区域,从而得出答案.现按函数的图象及其渐进线将平面直角坐标系划分为如图所示的几个区域,因为轴为两条渐近线,所以在区域(1)及区域(5)中可作的切线条数为0,在区域(2)中可作的切线条数为2,在区域(3)(4)中可作的切线条数为1,由题意可得点位于第(2)区域,即可得,从而可得答案成立.
二 多选题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,有选错的得0分,部分选对的得2分.
9 10 11 12
BCD AC BC BD
9.BCD 利用赋值法计算的值,再利用展开的通项公式获得具体项.令代入二项式可得各项的系数和为,即可得正确;对于,设展开式的通项为,当为常数项时,则有,则可得.代入二项式,可得展开式的常数项为,故错误;对于,因为,可得展开式中二项式系数最大的项仅有一项为第四项,故正确;对于,该展开式的通项为,可得展开式中的指数均为偶数.故D成立.故选BCD.
10.AC 利用函数的奇偶性及单调性结合不等式可得所满足的关系式,再结合上述关系分别验证答案是否成立.利用函数的性质可以判断为奇函数,且在上单调递增,由,可得,即有.所以A,C显然成立,D错误;令,可验证B错误.
11.BC 方法一:利用向量的加法公式可得两个三角函数所满足的关系式,再结合三角恒等变换获得对应的表达式的值.方法二:根据三角函数的定义,角的始边与非负半轴重合,终边与单位圆的交点为,画出图形,利用图形的几何性质求解,即利用数形结合思想求解.
方法一:,即有,故错误;利用向量的加法可得,,根据诱导公式及同角三角函数的关系,解得,故正确,且此时,即有,所以,D错误.
方法二:根据三角函数的定义,角的始边与非负半轴重合,终边分别经过单位圆上的两点,设,易知四边形为菱形,由图可知,后面判断方法同方法一.
12.BD 题需在不同的平面内构造平行线,将平面进行扩展,发现其与正方体各个面上的交线,从而获得截面的形状.如图,当点与两点不重合时,将线段向两端延长,分别交的延长线于点,连接分别交于两点,连接,此时截面为五边形MPSNR,故B正确;当点与点或点重合时,截面为四边形,不可能为六边形,故不正确;考虑,当点与点重合时,,,此时因为,故为钝角,所以错误;当点与点重合时,点到直线的距离取到最大值,此时的面积取到最大值,最大值为,故D成立.
三 填空题:本题共4小题,每小题5分,共20分.
13.【答案】
【解析】利用导数的几何意义求得切线的斜率,从而获得切线方程.对函数求导可得,把代入可得,则切线方程的斜率.又因为,所以切点为,从而可得切线方程为.
14.【答案】8
【解析】利用等差数列的性质以及韦达定理即可求解.根据韦达定理可得,利用等差数列的性质可得,从而可得.
15.【答案】1
【解析】根据切线方程及渐近线方程计算出关于,点的表达式,再利用向量的数量积进行求解.双曲线在点处的切线方程为,设点的坐标为,点的坐标为,代入的方程可得,
.两者相乘得,因为为双曲线上的点,所以.向量的数量积,将代入可得.本题还可通过特殊值进行求解.
16.【答案】;
【解析】本题需利用勾股定理以及平面图形的几何性质进行求解,第二空需要选择恰当的角度表示出的值,再利用三角恒等变换以及三角函数的性质求解出最值.
(1)时,,过点作于点,在Rt中,,在中,由余弦定理可计算得.
(2)设,则,过点分别作的垂线于两点,则,在与中,易得,,所以,当时,.
四 解答题:本题共6小题,共70分,解答题写出文字说明 证明过程或演算步骤.
17.【答案】(1)设数列的公比为,依题意可得
解得或,又因为数列的各项均为正数,所以.
从而可求得,
所以,.
(2),
【解析】先利用基本量法对条件进行化简获得的通项公式,再利用裂项相消的技巧进行求和.
18.【答案】(1)由正弦定理为外接圆半径)
可得,
代入中得
,
又,
所以
展开化简得
展开化简得
(2)由余弦定理及三角形面积公式得
,可解得.
【解析】先利用正弦定理对条件进行化简计算角的值,再利用余弦定理以及面积公式计算三角形的另外两条边.
19.【答案】(1)设点为的一个三等分点,且,连接,如图所示.
,且
又,且,从而可得,且.
综上可知四边形是平行四边形.
平面平面,
平面
(2)因为平面平面,平面平面,
,且平面,从而可得平面.
又由平面,所以,从而可得为二面角的平面角.
由题意可得,由,即有为等边三角形.
方法一:几何法
如图,过点作的垂线,垂足为,连接.
平面平面,平面平面,
,且平面,从而可得平面.
故为直线与平面所成角.
根据第(1)问的可知,所以,故
.
因为为等边三角形,所以的高为,
根据三角形的相似关系可得,
所以在Rt中,可得
所以直线与平面所成角的正弦值为
方法二:向量法
如图,以的中点为原点,为轴,过点在平面内作
的垂线为轴,为轴建立空间直角坐标系.
则有.
则有.
平面的一个法向量为
可得.
直线与平面所成角的正弦值为.
【解析】通过构造辅助线证明线面平行;利用二面角信息计算图形中相关的几何信息,接着根据定义作出线面角,再结合正 余弦定理进行求解,也可通过建立空间直角坐标系进行求解.
20.【答案】(1)根据频率分布直方图的信息,成绩在,对应的频率分别为.
根据总的频率和为1,可得成绩在所对应的频率为.
,且,可知成绩在内的前也属于第一档.即可知第一档的分数段为,第二档的分数段为
(2)根据第(1)问的结论可知,甲的成绩属于第三档,乙的成绩属于第二档,丙的成绩属于第一档.则的所有可能取值为
其中
则的分布列为:
0 1 2 3
的数学期望为:,
(注:写对一个概率得1分)
【解析】利用频率分布直方图中的概率和为1即可求得成绩位于分数段时的频率,进而结合题于信息求得每一档对应的分数段;再根据每位考生的总分是否上特控线的相互独立性,计算各种情况下的概率,最后完善分布列以及计算数学期望.
21.【答案】(1)由椭圆的焦距为,可得,即有.
设点的纵坐标为的面积,
其中,根据面积的最大值为,可得.
由椭圆的性质可得:.
于是椭圆的方程为.
(2)当直线的斜率为0时,以为直径的圆的方程为
圆与轴的交点为
当直线的斜率不为0时,设直线.
将直线与椭圆联立,可得.
设点的坐标分别为,则有
以为直径的圆的方程为
令,可得:①.
其中②,
③.
②③代入①可得④.
式子④可变换为⑤.
当,且时,⑤式成立,可解得.
综上可得,以为直径的圆恒过轴上的定点.
【解析】先利用椭圆相关的几何性质以及三个参数之间的关系计算出椭圆的方程,根据直线与椭圆的关系求得点的坐标所满足的关系式,再利用圆的方程观察其所经过的定点.本题的一个难点在于根据(1)式求得定点,本题可通过验证当直线为特殊直线时,对应圆的方程来猜想出所经过的定点,再反向验证(1)恒成立.例如,可令直线为:或进行求解.
22.【答案】(1)当时,,
对函数求导,可得,
在上,;在上,.即可得在上单调递减,在上单调递增;
由此可得,的最小值为,无最大值.
(2)对函数求导可得.当时,在上恒成立,即可得在上单调递增;故可得函数至多只有一个零点,不符合题意;
当时,令,设该方程的解为.在上,;在上,.即可得在上单调递减,在上单调递增;
为了满足有两个零点,则有①
因为是方程的解,所以,两边取对数可得②,
将②式代入①式可得,所以的取值范围为.
且当时,由②式得,所以在上仅有1个零点;当时,,故可得在上仅有1个零点;
综上,若函数存在两个零点,则实数的取值范围是.
【解析】先根据导数判断函数的单调性及最值,通过分类讨论确定函数的图象,从而判定实数的取值范围.
揭阳市2022届高三上学期期末考试
数学
本试卷共4页,考试时间120分钟,满分150分
注意事项:
1.答题前,考生先将自已的信息填写清楚 准确,将条形码准确粘贴在条形码粘贴处.
2.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效.
3.答题时请按要求用笔,保持卡面清洁,不要折叠,不要弄破 弄波,不得使用涂改液 修正带 刮纸刀.考试结束后,请将本试卷及答题卡交回.
一 选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设集合,则( )
A. B.
C. D.
2.复数满足为虚数单位,则的模为( )
A. B. C.1 D.
3.袋中有大小和形状都相同的3个白球和2个黑球,现从袋中不放回地依次抽取两个球,则在第一次取到白球的条件下,第二次也取到白球的概率是( )
A. B. C. D.
4.每年的毕业季都是高校毕业生求职和公司招聘最忙碌的时候,甲 乙两家公司今年分别提供了2个和3个不同的职位,一共收到了100份简历,具体数据如下:
公司 文史男 文史女 理工男 理工女
甲 10 10 20 10
乙 15 20 10 5
分析毕业生的选择意愿与性别的关联关系时,已知对应的的观测值;分析毕业生的选择意愿与专业关联的的观测值,则下列说法正确的是( )
A.有的把握认为毕业生的选择意愿与专业相关联
B.毕业生在选择甲 乙公司时,选择意愿与专业的关联比与性别的关联性更大一些
C.理科专业的学生更倾向于选择乙公司
D.女性毕业生更倾向于选择甲公司
5.已知函数,则该函数的增区间为( )
A.
B.
C.
D.
6.已知圆柱的轴截面为正方形,其外接球为球,则圆柱的表面积与球的表面积之比为( )
A. B. C. D.不能确定
7.已知过抛物线的焦点的直线交于两点(点在点的右边),为原点.若的重心的横坐标为10,则的值为( )
A.144 B.72 C.60 D.48
8.已知函数,过点可作两条直线与函数相切,则下列结论正确的是( )
A. B.
C.的最大值为2 D.
二 多选题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.已知二项式的展开式中各项的系数和为64,则下列说法正确的是( )
A.展开式中的常数项为1
B.
C.展开式中二项式系数最大的项是第四项
D.展开式中的指数均为偶数
10.已知函数,实数满足不等式,则( )
A. B.
C. D.
11.已知向量,且,则下列说法正确的是( )
A. B.
C. D.的最大值为2
12.如图所示,已知正方体的棱长为分别是的中点,是线段上的动点,则下列说法正确的是( )
A.平面截正方体所得的截面可以是四边形 五边形或六边形
B.当点与两点不重合时,平面截正方体所得的截面是五边形
C.是锐角三角形
D.面积的最大值是
三 填空题:本题共4小题,每小题5分,共20分.
13.已知函数,该函数在处的切线方程为__________.
14.在等差数列中,分别是方程的两个根,则__________.
15.如图所示,已知是双曲线右支上任意一点,双曲线在点处的切线分别与两条渐近线交于两点,则__________.
16.如图所示,在等腰直角中,为的中点,,分别为线段上的动点,且.
(1)当时,则的值为__________.
(2)的最大值为__________.
四 解答题:本题共6小题,共70分.解答应写出文字说明 证明过程或演算步骤.
17.(10分)
在各项均为正数的等比数列中,.
(1)求数列的通项公式;
(2),求数列的前项和.
18.(12分)
在中,角所对的边分别为,且.
(1)求角;
(2)若,且的面积为,且,求和的值.
19.(12分)
如图,在四棱锥中,底面为梯形,,平面平面为棱上的点,且.
(1)求证:平面;
(2)若,二面角为,求直线与平面所成角的正弦值.
20.(12分)
在高考结束后,省考试院会根据所有考生的成绩划分出特控线和本科线.考生们可以将自己的成绩与划线的对比作为高考志愿填报的决策依据.每一个学科的评价都有一个标准进行判断.以数学学科为例,在一次考试中,将考生的成绩由高到低排列,分为一 二 三档,前定为一档,前到前定为二档,后定为三档.在一次全市的模拟考试中,考生数学成绩的频率分布直方图如图所示,根据直方图的信息可知第三档的分数段为.
(1)求成绩位于时所对应的频率,并估计第二档和第一档的分数段;
(2)在历年的统计中发现,数学成绩为一档的考生其总分过特控线的概率为,数学成绩为二档的考生其总分过特控线的概率为,数学成绩为三档的考生其总分过特控线的概率为.在此次模拟考试中,甲 乙 丙三位考生的数学成绩分别为.请结合第(1)问中的分数段,求这三位考生总分上特控线的人数的分布列及数学期望.
21.(12分)
已知椭圆为椭圆的左 右焦点,焦距为,点在上,且面积的最大值为.
(1)求椭圆的方程;
(2)过点作直线交椭圆于两点,以为直径的圆是否恒过轴上的定点?若存在该定点,请求出的值;若不存在,请说明理由.
22.(12分)
已知函数
(1)若,判断函数的单调性,并求出函数的最值.
(2)若函数有两个零点,求实数的取值范围.
揭阳市2022届高三上学期期末考试
数学
试卷参考答案与评分标准
一 选择题:本题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1 2 3 4 5 6 7 8
D C C B C A D B
1.D 先将集合分别化简,再求其交集.,从而.
2.C 先做除法运算求出复数,再根据复数模的计算公式求其模.由得,从而
3.C 此题为条件概率模型,可以有两种做法:一是根据条件概率的公式计算;二是缩小样本空间的方法术解.
方法一:记第次取得白球为事件;
方法二:第一次取到白球后,袋中还有4个球,两白两黑,故第二次取出白球的概率为.
4.B 根据的观测值的意义再结合所给表格中的参考数据进行判断.与专业关联的的观测值,明显大于,明显小于,故仅有的把握认为毕业生的选择意原与专业相关联,所以不正确;因为,故正确;根据题中的数据表列出专业与甲 乙公司的关联表可知,理科专业的学生更倾向于选择甲公司,列出性别与甲 乙公司的关联表可知,女性毕业生更倾向于选择C公司,所以C,D均不对.
5.C 利用整体代换法和复合函数的单调性求函数的增区间.令,解得,故答案为C.
6.A 利用圆柱的轴截面信息求出圆柱的底面半径与高的关系,再结合圆柱与外接球的关系求得对应的比例关系.因为圆柱的轴截面为正方形,设圆柱底面圆的半径为,其高,其外接球的半径,则圆柱的表面积,球的表面积,则有,故答案为.
7.D 利用三角形的重心公式可得点的坐标所满足的关系,结合焦点弦长与点的坐标关系求得的值.抛物线的焦点,准线设点的坐标分别为,根据重心坐标公式得,可得.根据抛物线的几何性质,得,故答案为D.
8.B 根据函数的图像及其渐进线将平面直角坐标系划分为不同的区域,在不同区域内的点作函数的切线的条数不同.由此获得点所在的区域,从而得出答案.现按函数的图象及其渐进线将平面直角坐标系划分为如图所示的几个区域,因为轴为两条渐近线,所以在区域(1)及区域(5)中可作的切线条数为0,在区域(2)中可作的切线条数为2,在区域(3)(4)中可作的切线条数为1,由题意可得点位于第(2)区域,即可得,从而可得答案成立.
二 多选题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,有选错的得0分,部分选对的得2分.
9 10 11 12
BCD AC BC BD
9.BCD 利用赋值法计算的值,再利用展开的通项公式获得具体项.令代入二项式可得各项的系数和为,即可得正确;对于,设展开式的通项为,当为常数项时,则有,则可得.代入二项式,可得展开式的常数项为,故错误;对于,因为,可得展开式中二项式系数最大的项仅有一项为第四项,故正确;对于,该展开式的通项为,可得展开式中的指数均为偶数.故D成立.故选BCD.
10.AC 利用函数的奇偶性及单调性结合不等式可得所满足的关系式,再结合上述关系分别验证答案是否成立.利用函数的性质可以判断为奇函数,且在上单调递增,由,可得,即有.所以A,C显然成立,D错误;令,可验证B错误.
11.BC 方法一:利用向量的加法公式可得两个三角函数所满足的关系式,再结合三角恒等变换获得对应的表达式的值.方法二:根据三角函数的定义,角的始边与非负半轴重合,终边与单位圆的交点为,画出图形,利用图形的几何性质求解,即利用数形结合思想求解.
方法一:,即有,故错误;利用向量的加法可得,,根据诱导公式及同角三角函数的关系,解得,故正确,且此时,即有,所以,D错误.
方法二:根据三角函数的定义,角的始边与非负半轴重合,终边分别经过单位圆上的两点,设,易知四边形为菱形,由图可知,后面判断方法同方法一.
12.BD 题需在不同的平面内构造平行线,将平面进行扩展,发现其与正方体各个面上的交线,从而获得截面的形状.如图,当点与两点不重合时,将线段向两端延长,分别交的延长线于点,连接分别交于两点,连接,此时截面为五边形MPSNR,故B正确;当点与点或点重合时,截面为四边形,不可能为六边形,故不正确;考虑,当点与点重合时,,,此时因为,故为钝角,所以错误;当点与点重合时,点到直线的距离取到最大值,此时的面积取到最大值,最大值为,故D成立.
三 填空题:本题共4小题,每小题5分,共20分.
13.【答案】
【解析】利用导数的几何意义求得切线的斜率,从而获得切线方程.对函数求导可得,把代入可得,则切线方程的斜率.又因为,所以切点为,从而可得切线方程为.
14.【答案】8
【解析】利用等差数列的性质以及韦达定理即可求解.根据韦达定理可得,利用等差数列的性质可得,从而可得.
15.【答案】1
【解析】根据切线方程及渐近线方程计算出关于,点的表达式,再利用向量的数量积进行求解.双曲线在点处的切线方程为,设点的坐标为,点的坐标为,代入的方程可得,
.两者相乘得,因为为双曲线上的点,所以.向量的数量积,将代入可得.本题还可通过特殊值进行求解.
16.【答案】;
【解析】本题需利用勾股定理以及平面图形的几何性质进行求解,第二空需要选择恰当的角度表示出的值,再利用三角恒等变换以及三角函数的性质求解出最值.
(1)时,,过点作于点,在Rt中,,在中,由余弦定理可计算得.
(2)设,则,过点分别作的垂线于两点,则,在与中,易得,,所以,当时,.
四 解答题:本题共6小题,共70分,解答题写出文字说明 证明过程或演算步骤.
17.【答案】(1)设数列的公比为,依题意可得
解得或,又因为数列的各项均为正数,所以.
从而可求得,
所以,.
(2),
【解析】先利用基本量法对条件进行化简获得的通项公式,再利用裂项相消的技巧进行求和.
18.【答案】(1)由正弦定理为外接圆半径)
可得,
代入中得
,
又,
所以
展开化简得
展开化简得
(2)由余弦定理及三角形面积公式得
,可解得.
【解析】先利用正弦定理对条件进行化简计算角的值,再利用余弦定理以及面积公式计算三角形的另外两条边.
19.【答案】(1)设点为的一个三等分点,且,连接,如图所示.
,且
又,且,从而可得,且.
综上可知四边形是平行四边形.
平面平面,
平面
(2)因为平面平面,平面平面,
,且平面,从而可得平面.
又由平面,所以,从而可得为二面角的平面角.
由题意可得,由,即有为等边三角形.
方法一:几何法
如图,过点作的垂线,垂足为,连接.
平面平面,平面平面,
,且平面,从而可得平面.
故为直线与平面所成角.
根据第(1)问的可知,所以,故
.
因为为等边三角形,所以的高为,
根据三角形的相似关系可得,
所以在Rt中,可得
所以直线与平面所成角的正弦值为
方法二:向量法
如图,以的中点为原点,为轴,过点在平面内作
的垂线为轴,为轴建立空间直角坐标系.
则有.
则有.
平面的一个法向量为
可得.
直线与平面所成角的正弦值为.
【解析】通过构造辅助线证明线面平行;利用二面角信息计算图形中相关的几何信息,接着根据定义作出线面角,再结合正 余弦定理进行求解,也可通过建立空间直角坐标系进行求解.
20.【答案】(1)根据频率分布直方图的信息,成绩在,对应的频率分别为.
根据总的频率和为1,可得成绩在所对应的频率为.
,且,可知成绩在内的前也属于第一档.即可知第一档的分数段为,第二档的分数段为
(2)根据第(1)问的结论可知,甲的成绩属于第三档,乙的成绩属于第二档,丙的成绩属于第一档.则的所有可能取值为
其中
则的分布列为:
0 1 2 3
的数学期望为:,
(注:写对一个概率得1分)
【解析】利用频率分布直方图中的概率和为1即可求得成绩位于分数段时的频率,进而结合题于信息求得每一档对应的分数段;再根据每位考生的总分是否上特控线的相互独立性,计算各种情况下的概率,最后完善分布列以及计算数学期望.
21.【答案】(1)由椭圆的焦距为,可得,即有.
设点的纵坐标为的面积,
其中,根据面积的最大值为,可得.
由椭圆的性质可得:.
于是椭圆的方程为.
(2)当直线的斜率为0时,以为直径的圆的方程为
圆与轴的交点为
当直线的斜率不为0时,设直线.
将直线与椭圆联立,可得.
设点的坐标分别为,则有
以为直径的圆的方程为
令,可得:①.
其中②,
③.
②③代入①可得④.
式子④可变换为⑤.
当,且时,⑤式成立,可解得.
综上可得,以为直径的圆恒过轴上的定点.
【解析】先利用椭圆相关的几何性质以及三个参数之间的关系计算出椭圆的方程,根据直线与椭圆的关系求得点的坐标所满足的关系式,再利用圆的方程观察其所经过的定点.本题的一个难点在于根据(1)式求得定点,本题可通过验证当直线为特殊直线时,对应圆的方程来猜想出所经过的定点,再反向验证(1)恒成立.例如,可令直线为:或进行求解.
22.【答案】(1)当时,,
对函数求导,可得,
在上,;在上,.即可得在上单调递减,在上单调递增;
由此可得,的最小值为,无最大值.
(2)对函数求导可得.当时,在上恒成立,即可得在上单调递增;故可得函数至多只有一个零点,不符合题意;
当时,令,设该方程的解为.在上,;在上,.即可得在上单调递减,在上单调递增;
为了满足有两个零点,则有①
因为是方程的解,所以,两边取对数可得②,
将②式代入①式可得,所以的取值范围为.
且当时,由②式得,所以在上仅有1个零点;当时,,故可得在上仅有1个零点;
综上,若函数存在两个零点,则实数的取值范围是.
【解析】先根据导数判断函数的单调性及最值,通过分类讨论确定函数的图象,从而判定实数的取值范围.
同课章节目录
