2020-2021学年上海市普陀区七年级(上)期末数学试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年上海市普陀区七年级(上)期末数学试卷(Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 308.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-18 09:31:22 | ||
图片预览




文档简介
2020-2021学年上海市普陀区七年级(上)期末数学试卷
一、选择题(本大题共6题,每题2分,满分12分)
1.(2分)下列代数式中,多项式是( )
A.x6 B.﹣ C.ax+b D.
2.(2分)下列运算结果中,正确的是( )
A.a2 a2=2a4 B.(﹣a)2=﹣a2 C.a2+a2=2a4 D.(2a)2=4a2
3.(2分)如果单项式3xm+1y4与﹣4x2yn是同类项,那么m+n的值是( )
A.5 B.1 C.4 D.6
4.(2分)下列等式中,从左到右是因式分解的是( )
A.﹣1=(+1) (﹣1) B.a2+2ab+b2=(a+b)2
C.am+bm﹣1=m(a+b)﹣1 D.(a+b)(a﹣b)=a2﹣b2
5.(2分)下列图形中既是轴对称图形又是中心对称图形的是( )
A.等边三角形 B.平行四边形 C.圆 D.等腰梯形
6.(2分)如果存在一条直线将一个图形分割成两部分,使其中一部分图形按某个方向平移后能够与另一部分重合,那么我们把这种图形称为平移重合图形,下列图形中,不是平移重合图形的是( )
A. 正方形
B. 长方形
C. 平行四边形
D. 圆
二、填空题(本大题共12题,每题3分,满分36分)
7.(3分)用代数式表示:“x的倒数与2021的和”是 .
8.(3分)单项式﹣ab2c的系数是 ,次数是 .
9.(3分)用科学记数法表示:0.00002021= .
10.(3分)合并同类项:2x2﹣9x2+4x2= .
11.(3分)已知一个多项式减去2x2﹣9x的结果等于x2+9x+1,那么这个多项式是 .
12.(3分)计算:(﹣2x﹣y)2= .
13.(3分)分解因式:x2﹣7x+12= .
14.(3分)对于分式,x的取值范围是 .
15.(3分)计算:+= .
16.(3分)将代数式化为只含有正整数指数幂的形式,其结果是 .
17.(3分)2020年上海某垃圾处理厂5月份分别从甲乙两社区各回收干垃圾a吨,据该垃圾处理厂统计,在6月份和7月份中,甲社区干垃圾平均每月的增长率是x,乙社区干垃圾平均每月的减少率是x,那么7月份甲社区比乙社区的干垃圾量多 吨.(结果用含a、x的代数式表示)
18.(3分)如图,三角形ABC是直角三角形,∠C=90°,∠B=60°,AB=6,如果将三角形ABC绕着点B旋转α(0°<α<180°),使得点A恰好落在直线BC上,点A的对应点记作点D,弧AD是点A旋转时运动的路径,那么弧AD的长是 .(结果保留π)
三、简答题(本大题共6题,每题4分,满分24分)
19.(4分)计算:(﹣2a)2 (3ab3)÷(4a2b2).
20.(4分)计算:(x+3y)(x﹣2y)﹣(2x+y)2.
21.(4分)分解因式:a2m4﹣13a2m2﹣48a2.
22.(4分)分解因式:a2+2ab﹣16+b2.
23.(4分)解方程:﹣3=.
24.(4分)计算:()﹣2×3﹣1+(π﹣2020)0÷()﹣1.
四、解答题(本大题共4题,第25、26题每题6分,第27、28题每题8分,满分28分)
25.(6分)如图,已知三角形ABC、直线l,点O是线段AB的中点.
(1)画出三角形ABC关于直线l的轴对称的图形;
(2)画出三角形ABC关于点O的中心对称的图形.
(不写画法,保留画图痕迹,并写出画图结论)
26.(6分)先化简,再求值:÷﹣1,其中x=1.
27.(8分)某校为了准备“迎新活动”,用900元购买了甲、乙两种礼品共240个,其中购买甲种礼品比乙种礼品少用了180元.
(1)购买甲种礼品一共用去 元;(请直接写出答案)
(2)如果甲种礼品的单价是乙种礼品单价的2倍,那么乙种礼品的单价是多少元?
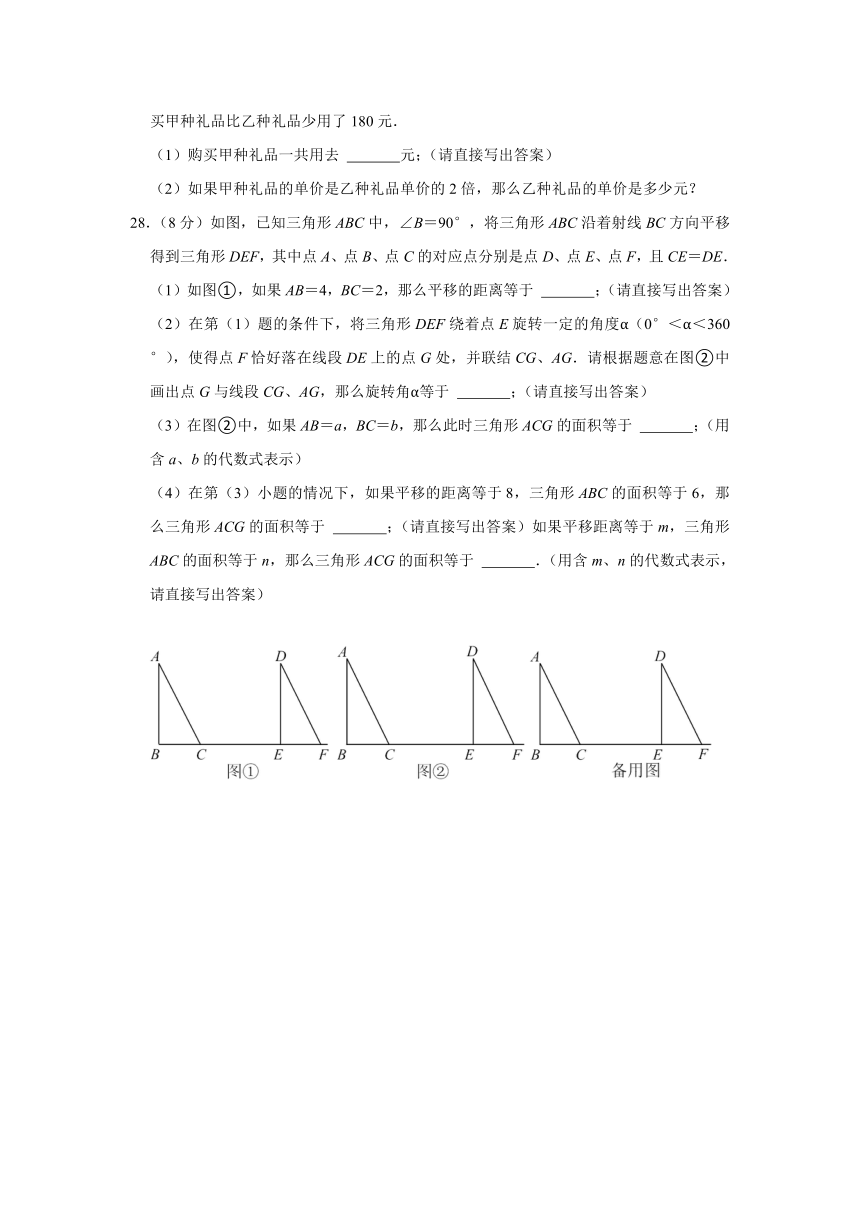
28.(8分)如图,已知三角形ABC中,∠B=90°,将三角形ABC沿着射线BC方向平移得到三角形DEF,其中点A、点B、点C的对应点分别是点D、点E、点F,且CE=DE.
(1)如图①,如果AB=4,BC=2,那么平移的距离等于 ;(请直接写出答案)
(2)在第(1)题的条件下,将三角形DEF绕着点E旋转一定的角度α(0°<α<360°),使得点F恰好落在线段DE上的点G处,并联结CG、AG.请根据题意在图②中画出点G与线段CG、AG,那么旋转角α等于 ;(请直接写出答案)
(3)在图②中,如果AB=a,BC=b,那么此时三角形ACG的面积等于 ;(用含a、b的代数式表示)
(4)在第(3)小题的情况下,如果平移的距离等于8,三角形ABC的面积等于6,那么三角形ACG的面积等于 ;(请直接写出答案)如果平移距离等于m,三角形ABC的面积等于n,那么三角形ACG的面积等于 .(用含m、n的代数式表示,请直接写出答案)
2020-2021学年上海市普陀区七年级(上)期末数学试卷
参考答案与试题解析
一、选择题(本大题共6题,每题2分,满分12分)
1.(2分)下列代数式中,多项式是( )
A.x6 B.﹣ C.ax+b D.
【分析】直接利用多项式的定义,几个单项式的和叫做多项式,进而得出答案.
【解答】解:A、x6是单项式,故不符合题意;
B、﹣是单项式,故不符合题意;
C、ax+b是多项式,故符合题意;
D、是分式,故不符合题意.
故选:C.
2.(2分)下列运算结果中,正确的是( )
A.a2 a2=2a4 B.(﹣a)2=﹣a2 C.a2+a2=2a4 D.(2a)2=4a2
【分析】A、根据同底数幂乘法的运算法则计算判断即可;B、根据积的乘方和幂的乘方运算法则计算即可判断;C、根据合并同类项法则判断即可;D、根据积的乘方和幂的乘方运算法则计算即可判断即可.
【解答】解:A、a2 a2=a4,故计算不正确;
B、(﹣a)2=a2,故计算不正确;
C、a2+a2=2a2,故计算不正确;
D、(2a)2=4a2,计算正确.
故选:D.
3.(2分)如果单项式3xm+1y4与﹣4x2yn是同类项,那么m+n的值是( )
A.5 B.1 C.4 D.6
【分析】利用同类项的定义求得m,n的值,将m,n的值代入计算即可得出结论.
【解答】解:∵单项式3xm+1y4与﹣4x2yn是同类项,
∴m+1=2,n=4,
解得:m=1,n=4.
∴m+n=1+4=5.
故选:A.
4.(2分)下列等式中,从左到右是因式分解的是( )
A.﹣1=(+1) (﹣1) B.a2+2ab+b2=(a+b)2
C.am+bm﹣1=m(a+b)﹣1 D.(a+b)(a﹣b)=a2﹣b2
【分析】根据因式分解的定义判断即可.
【解答】解:A选项,不是整式,故该选项不符合题意;
B选项,a2+2ab+b2=(a+b)2,故该选项符合题意;
C选项,等式的右边不是积的形式,故该选项不符合题意;
D选项,等式的右边不是积的形式,故该选项不符合题意;
故选:B.
5.(2分)下列图形中既是轴对称图形又是中心对称图形的是( )
A.等边三角形 B.平行四边形 C.圆 D.等腰梯形
【分析】根据轴对称图形和中心对称图形的概念,对各选项分析判断即可得解.把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形;如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形.
【解答】解:A.等边三角形是轴对称图形,不是中心对称图形,故本选项不符合题意;
B.平行四边形不是轴对称图形,是中心对称图形,故本选项不符合题意;
C.圆既是轴对称图形,又是中心对称图形,故本选项符合题意;
D.等腰梯形是轴对称图形,不是中心对称图形,故本选项不符合题意.
故选:C.
6.(2分)如果存在一条直线将一个图形分割成两部分,使其中一部分图形按某个方向平移后能够与另一部分重合,那么我们把这种图形称为平移重合图形,下列图形中,不是平移重合图形的是( )
A. 正方形
B. 长方形
C. 平行四边形
D. 圆
【分析】证明平行四边形、长方形、正方形是平移重合图形即可.
【解答】解:如图,平行四边形ABCD中,取BC,AD的中点E,F,连接EF.
∵四边形ABEF向右平移可以与四边形EFDC重合,
∴平行四边形ABCD是平移重合图形,
∴长方形和正方形也是平移重合图形,
故选:D.
二、填空题(本大题共12题,每题3分,满分36分)
7.(3分)用代数式表示:“x的倒数与2021的和”是 +2021 .
【分析】用x的倒数加上2021即可.
【解答】解:根据题意可知,“x的倒数与2021的和”是+2021.
故答案为:+2021.
8.(3分)单项式﹣ab2c的系数是 ﹣ ,次数是 4 .
【分析】根据单项式的系数和次数的定义即可得出答案.
【解答】解:单项式﹣2x3的系数和次数分别﹣,4,
故答案为:﹣,4.
9.(3分)用科学记数法表示:0.00002021= 2.021×10﹣5 .
【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负整数指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
【解答】解:0.00002021=2.021×10﹣5.
故答案为:2.021×10﹣5.
10.(3分)合并同类项:2x2﹣9x2+4x2= ﹣3x2 .
【分析】利用合并同类项的法则进行计算即可.
【解答】解:原式=(2﹣9+4)x2=﹣3x2,
故答案为:﹣3x2.
11.(3分)已知一个多项式减去2x2﹣9x的结果等于x2+9x+1,那么这个多项式是 3x2+1 .
【分析】先根据题意列出算式(x2+9x+1)+(2x2﹣9x),再去括号、合并同类项即可.
【解答】解:根据题意,这个多项式为(x2+9x+1)+(2x2﹣9x)
=x2+9x+1+2x2﹣9x
=3x2+1,
故答案为:3x2+1.
12.(3分)计算:(﹣2x﹣y)2= 4x2+4xy+y2 .
【分析】根据完全平方公式化简即可.
【解答】解:原式=[﹣(2x+y)]2
=(2x+y)2
=4x2+4xy+y2,
故答案为:4x2+4xy+y2.
13.(3分)分解因式:x2﹣7x+12= (x﹣3)(x﹣4) .
【分析】因为(﹣3)×(﹣4)=12,(﹣3)+(﹣4)=﹣7,所以利用十字相乘法分解因式即可.
【解答】解:x2﹣7x+12=(x﹣3)(x﹣4).
故答案为:(x﹣3)(x﹣4).
14.(3分)对于分式,x的取值范围是 x≠1 .
【分析】根据分式的分母不为0列出不等式,解不等式即可.
【解答】解:由题意得:x﹣1≠0,
解得:x≠1,
故答案为:x≠1.
15.(3分)计算:+= .
【分析】先通分,再按照同分母分式的运算法则计算即可.
【解答】解:原式===.
故答案为:.
16.(3分)将代数式化为只含有正整数指数幂的形式,其结果是 .
【分析】根据负整数指数幂:a﹣p=(a≠0,p为正整数)进行计算即可.
【解答】解:=,
故答案为:,
17.(3分)2020年上海某垃圾处理厂5月份分别从甲乙两社区各回收干垃圾a吨,据该垃圾处理厂统计,在6月份和7月份中,甲社区干垃圾平均每月的增长率是x,乙社区干垃圾平均每月的减少率是x,那么7月份甲社区比乙社区的干垃圾量多 4ax 吨.(结果用含a、x的代数式表示)
【分析】分别表示出甲、乙社区7月份干垃圾量,相减即可得答案.
【解答】解:∵5月份分别从甲乙两社区各回收干垃圾a吨,6月份和7月份甲社区干垃圾平均每月的增长率是x,乙社区干垃圾平均每月的减少率是x,
∴7月份甲社区的干垃圾量为a(1+x)2,乙社区的干垃圾量为a(1﹣x)2,
∴7月份甲社区比乙社区的干垃圾量多a(1+x)2﹣a(1﹣x)2=a(1+2x+x2)﹣a(1﹣2x+x2)=a+2ax+ax2﹣a+2ax﹣ax2=4ax,
故答案为:4ax.
18.(3分)如图,三角形ABC是直角三角形,∠C=90°,∠B=60°,AB=6,如果将三角形ABC绕着点B旋转α(0°<α<180°),使得点A恰好落在直线BC上,点A的对应点记作点D,弧AD是点A旋转时运动的路径,那么弧AD的长是 4π或2π .(结果保留π)
【分析】分别画出图形,根据弧长计算公式及可得答案.
【解答】解:当将三角形ABC绕着点B逆时针旋转α(0°<α<180°),使得点A恰好落在直线BC上,点A的对应点记作点D,如图:
∵∠ABC=60°,
∴α=180°﹣∠ABC=120°,
∴弧AD的长是=4π,
当将三角形ABC绕着点B顺时针旋转α(0°<α<180°),使得点A恰好落在直线BC上,点A的对应点记作点D,如图:
∴弧AD的长是=2π,
综上所述,弧AD的长是4π或2π,
故答案为:4π或2π.
三、简答题(本大题共6题,每题4分,满分24分)
19.(4分)计算:(﹣2a)2 (3ab3)÷(4a2b2).
【分析】先计算单项式的乘方、将除法转化为乘法,再计算乘法即可.
【解答】解:原式=4a2 3ab3÷4a2b2
=12a3b3÷4a2b2
=3ab.
20.(4分)计算:(x+3y)(x﹣2y)﹣(2x+y)2.
【分析】根据多项式乘多项式和完全平方公式化简即可.
【解答】解:原式=x2﹣2xy+3xy﹣6y2﹣(4x2+4xy+y2)
=x2﹣2xy+3xy﹣6y2﹣4x2﹣4xy﹣y2
=﹣3x2﹣3xy﹣7y2.
21.(4分)分解因式:a2m4﹣13a2m2﹣48a2.
【分析】先提公因式,然后再利用十字相乘法,最后利用平方差公式继续分解即可.
【解答】解:a2m4﹣13a2m2﹣48a2
=a2(m4﹣13m2﹣48)
=a2(m2﹣16)(m2+3)
=a2(m+4)(m﹣4)(m2+3).
22.(4分)分解因式:a2+2ab﹣16+b2.
【分析】将a2+2ab+b2分为一组,用完全平方公式分解因式,再用平方差公式分解因式即可.
【解答】解:原式=(a2+2ab+b2)﹣16
=(a+b)2﹣42
=(a+b+4)(a+b﹣4).
23.(4分)解方程:﹣3=.
【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
【解答】解:去分母得:6﹣3(x+7)=2x,
去括号得:6﹣3x﹣21=2x,
移项合并得:﹣5x=15,
解得:x=﹣3,
经检验x=﹣3是分式方程的解.
24.(4分)计算:()﹣2×3﹣1+(π﹣2020)0÷()﹣1.
【分析】先计算负整数指数幂和零指数幂的运算,再计算乘法运算,最后算加减.
【解答】解:原式=()2×+1÷4
=×+
=1.
四、解答题(本大题共4题,第25、26题每题6分,第27、28题每题8分,满分28分)
25.(6分)如图,已知三角形ABC、直线l,点O是线段AB的中点.
(1)画出三角形ABC关于直线l的轴对称的图形;
(2)画出三角形ABC关于点O的中心对称的图形.
(不写画法,保留画图痕迹,并写出画图结论)
【分析】(1)利用轴对称的性质分别作出A,B,C的对应点A′,B′,C′即可;
(2)作出点C关于点O的对应点D,连接BD,AD,△ABD即为所求.
【解答】解:(1)如图,△A′B′C′即为所求;
(2)如图,△ABD即为所求.
26.(6分)先化简,再求值:÷﹣1,其中x=1.
【分析】先根据分式的混合运算顺序和运算法则化简原式,再将x的值代入计算即可.
【解答】解:原式= ﹣1
=﹣1
=﹣
=,
当x=1时,
原式==﹣.
27.(8分)某校为了准备“迎新活动”,用900元购买了甲、乙两种礼品共240个,其中购买甲种礼品比乙种礼品少用了180元.
(1)购买甲种礼品一共用去 360 元;(请直接写出答案)
(2)如果甲种礼品的单价是乙种礼品单价的2倍,那么乙种礼品的单价是多少元?
【分析】(1)设买甲种礼品花了x元,则买乙种礼品花了(x+180)元,由题意:用900元购买了甲、乙两种礼品,列出一元一次方程,解方程即可;
(2)设乙种礼品的单价为a元,则甲种礼品的单价为2a元,由题意:用900元购买了甲、乙两种礼品共240个,列出分式方程,解方程即可.
【解答】解:(1)设买甲种礼品花了x元,则买乙种礼品花了(x+180)元,
根据题意,得:x+x+180=900,
解得:x=360,
即买甲种礼品一共用去360元,
故答案为:360;
(2)设乙种礼品的单价为a元,则甲种礼品的单价为2a元,
根据题意,得:+=240
解得:a=3,
经检验:a=3是原分式方程的解,且符合题意,
答:乙种礼品的单价为3元.
28.(8分)如图,已知三角形ABC中,∠B=90°,将三角形ABC沿着射线BC方向平移得到三角形DEF,其中点A、点B、点C的对应点分别是点D、点E、点F,且CE=DE.
(1)如图①,如果AB=4,BC=2,那么平移的距离等于 6 ;(请直接写出答案)
(2)在第(1)题的条件下,将三角形DEF绕着点E旋转一定的角度α(0°<α<360°),使得点F恰好落在线段DE上的点G处,并联结CG、AG.请根据题意在图②中画出点G与线段CG、AG,那么旋转角α等于 90°或270° ;(请直接写出答案)
(3)在图②中,如果AB=a,BC=b,那么此时三角形ACG的面积等于 ;(用含a、b的代数式表示)
(4)在第(3)小题的情况下,如果平移的距离等于8,三角形ABC的面积等于6,那么三角形ACG的面积等于 20 ;(请直接写出答案)如果平移距离等于m,三角形ABC的面积等于n,那么三角形ACG的面积等于 ﹣2n .(用含m、n的代数式表示,请直接写出答案)
【分析】(1)由平移的性质可得△ABC≌△DEF,可得AB=DE=4=CE,即可求解;
(2)由旋转的性质直接可求解;
(3)由“SAS”可证△ABC≌△CEG,可得AC=CG,∠BAC=∠GCE,可证△ACG是等腰直角三角形,由勾股定理和三角形面积公式可求解;
(4)由完全平方公式可求BC2+AB2的值,由勾股定理和等腰直角三角形的面积公式可求解.
【解答】解:(1)∵将△ABC沿着射线BC方向平移得到△DEF,
∴△ABC≌△DEF,
∴AB=DE=4,
∵CE=DE,
∴CE=4,
∴平移距离=BC+CE=4+2=6,
故答案为:6;
(2)如图②,点G为所求点,
∴△DEF绕着点E顺时针旋转270°或△DEF绕着点E逆时针旋转90°,
故答案为:90°或270°;
(3)如图②,由折叠可知:GE=EF,
又∵AB=CE,∠ABC=∠CEG=90°,
∴△ABC≌△CEG(SAS),
∴AC=CG,∠BAC=∠GCE,
∵∠BAC+∠ACB=90°,
∴∠ACB+∠GCE=90°,
∴∠ACG=90°,
∴△ACG是等腰直角三角形,
∵AB=a,BC=b,
∴AC==,
∴S△ACG=×AC2=,
故答案为:;
(4)若平移的距离等于8,三角形ABC的面积等于6,
∴BC+CE=8,×AB×BC=6,
∵AB=CE=DE,
∴BC+AB=8,AB×BC=12,
∴BC2+AB2+2AB BC=64,
∴BC2+AB2=40,
∵AC2=BC2+AB2,
∴AC2=40,
∵△ACG是等腰直角三角形,
∴S△ACG=×AC2=20;
若平移距离等于m,三角形ABC的面积等于n,
∴BC+CE=m,×AB×BC=n,
∵AB=CE=DE,
∴BC+AB=m,AB×BC=2n,
∴BC2+AB2+2AB BC=m2,
∴BC2+AB2=m2﹣4n,
∵AC2=BC2+AB2,
∴AC2=m2﹣4n,
∵△ACG是等腰直角三角形,
∴S△ACG=×AC2=﹣2n,
故答案为:20,﹣2n.
一、选择题(本大题共6题,每题2分,满分12分)
1.(2分)下列代数式中,多项式是( )
A.x6 B.﹣ C.ax+b D.
2.(2分)下列运算结果中,正确的是( )
A.a2 a2=2a4 B.(﹣a)2=﹣a2 C.a2+a2=2a4 D.(2a)2=4a2
3.(2分)如果单项式3xm+1y4与﹣4x2yn是同类项,那么m+n的值是( )
A.5 B.1 C.4 D.6
4.(2分)下列等式中,从左到右是因式分解的是( )
A.﹣1=(+1) (﹣1) B.a2+2ab+b2=(a+b)2
C.am+bm﹣1=m(a+b)﹣1 D.(a+b)(a﹣b)=a2﹣b2
5.(2分)下列图形中既是轴对称图形又是中心对称图形的是( )
A.等边三角形 B.平行四边形 C.圆 D.等腰梯形
6.(2分)如果存在一条直线将一个图形分割成两部分,使其中一部分图形按某个方向平移后能够与另一部分重合,那么我们把这种图形称为平移重合图形,下列图形中,不是平移重合图形的是( )
A. 正方形
B. 长方形
C. 平行四边形
D. 圆
二、填空题(本大题共12题,每题3分,满分36分)
7.(3分)用代数式表示:“x的倒数与2021的和”是 .
8.(3分)单项式﹣ab2c的系数是 ,次数是 .
9.(3分)用科学记数法表示:0.00002021= .
10.(3分)合并同类项:2x2﹣9x2+4x2= .
11.(3分)已知一个多项式减去2x2﹣9x的结果等于x2+9x+1,那么这个多项式是 .
12.(3分)计算:(﹣2x﹣y)2= .
13.(3分)分解因式:x2﹣7x+12= .
14.(3分)对于分式,x的取值范围是 .
15.(3分)计算:+= .
16.(3分)将代数式化为只含有正整数指数幂的形式,其结果是 .
17.(3分)2020年上海某垃圾处理厂5月份分别从甲乙两社区各回收干垃圾a吨,据该垃圾处理厂统计,在6月份和7月份中,甲社区干垃圾平均每月的增长率是x,乙社区干垃圾平均每月的减少率是x,那么7月份甲社区比乙社区的干垃圾量多 吨.(结果用含a、x的代数式表示)
18.(3分)如图,三角形ABC是直角三角形,∠C=90°,∠B=60°,AB=6,如果将三角形ABC绕着点B旋转α(0°<α<180°),使得点A恰好落在直线BC上,点A的对应点记作点D,弧AD是点A旋转时运动的路径,那么弧AD的长是 .(结果保留π)
三、简答题(本大题共6题,每题4分,满分24分)
19.(4分)计算:(﹣2a)2 (3ab3)÷(4a2b2).
20.(4分)计算:(x+3y)(x﹣2y)﹣(2x+y)2.
21.(4分)分解因式:a2m4﹣13a2m2﹣48a2.
22.(4分)分解因式:a2+2ab﹣16+b2.
23.(4分)解方程:﹣3=.
24.(4分)计算:()﹣2×3﹣1+(π﹣2020)0÷()﹣1.
四、解答题(本大题共4题,第25、26题每题6分,第27、28题每题8分,满分28分)
25.(6分)如图,已知三角形ABC、直线l,点O是线段AB的中点.
(1)画出三角形ABC关于直线l的轴对称的图形;
(2)画出三角形ABC关于点O的中心对称的图形.
(不写画法,保留画图痕迹,并写出画图结论)
26.(6分)先化简,再求值:÷﹣1,其中x=1.
27.(8分)某校为了准备“迎新活动”,用900元购买了甲、乙两种礼品共240个,其中购买甲种礼品比乙种礼品少用了180元.
(1)购买甲种礼品一共用去 元;(请直接写出答案)
(2)如果甲种礼品的单价是乙种礼品单价的2倍,那么乙种礼品的单价是多少元?
28.(8分)如图,已知三角形ABC中,∠B=90°,将三角形ABC沿着射线BC方向平移得到三角形DEF,其中点A、点B、点C的对应点分别是点D、点E、点F,且CE=DE.
(1)如图①,如果AB=4,BC=2,那么平移的距离等于 ;(请直接写出答案)
(2)在第(1)题的条件下,将三角形DEF绕着点E旋转一定的角度α(0°<α<360°),使得点F恰好落在线段DE上的点G处,并联结CG、AG.请根据题意在图②中画出点G与线段CG、AG,那么旋转角α等于 ;(请直接写出答案)
(3)在图②中,如果AB=a,BC=b,那么此时三角形ACG的面积等于 ;(用含a、b的代数式表示)
(4)在第(3)小题的情况下,如果平移的距离等于8,三角形ABC的面积等于6,那么三角形ACG的面积等于 ;(请直接写出答案)如果平移距离等于m,三角形ABC的面积等于n,那么三角形ACG的面积等于 .(用含m、n的代数式表示,请直接写出答案)
2020-2021学年上海市普陀区七年级(上)期末数学试卷
参考答案与试题解析
一、选择题(本大题共6题,每题2分,满分12分)
1.(2分)下列代数式中,多项式是( )
A.x6 B.﹣ C.ax+b D.
【分析】直接利用多项式的定义,几个单项式的和叫做多项式,进而得出答案.
【解答】解:A、x6是单项式,故不符合题意;
B、﹣是单项式,故不符合题意;
C、ax+b是多项式,故符合题意;
D、是分式,故不符合题意.
故选:C.
2.(2分)下列运算结果中,正确的是( )
A.a2 a2=2a4 B.(﹣a)2=﹣a2 C.a2+a2=2a4 D.(2a)2=4a2
【分析】A、根据同底数幂乘法的运算法则计算判断即可;B、根据积的乘方和幂的乘方运算法则计算即可判断;C、根据合并同类项法则判断即可;D、根据积的乘方和幂的乘方运算法则计算即可判断即可.
【解答】解:A、a2 a2=a4,故计算不正确;
B、(﹣a)2=a2,故计算不正确;
C、a2+a2=2a2,故计算不正确;
D、(2a)2=4a2,计算正确.
故选:D.
3.(2分)如果单项式3xm+1y4与﹣4x2yn是同类项,那么m+n的值是( )
A.5 B.1 C.4 D.6
【分析】利用同类项的定义求得m,n的值,将m,n的值代入计算即可得出结论.
【解答】解:∵单项式3xm+1y4与﹣4x2yn是同类项,
∴m+1=2,n=4,
解得:m=1,n=4.
∴m+n=1+4=5.
故选:A.
4.(2分)下列等式中,从左到右是因式分解的是( )
A.﹣1=(+1) (﹣1) B.a2+2ab+b2=(a+b)2
C.am+bm﹣1=m(a+b)﹣1 D.(a+b)(a﹣b)=a2﹣b2
【分析】根据因式分解的定义判断即可.
【解答】解:A选项,不是整式,故该选项不符合题意;
B选项,a2+2ab+b2=(a+b)2,故该选项符合题意;
C选项,等式的右边不是积的形式,故该选项不符合题意;
D选项,等式的右边不是积的形式,故该选项不符合题意;
故选:B.
5.(2分)下列图形中既是轴对称图形又是中心对称图形的是( )
A.等边三角形 B.平行四边形 C.圆 D.等腰梯形
【分析】根据轴对称图形和中心对称图形的概念,对各选项分析判断即可得解.把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形;如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形.
【解答】解:A.等边三角形是轴对称图形,不是中心对称图形,故本选项不符合题意;
B.平行四边形不是轴对称图形,是中心对称图形,故本选项不符合题意;
C.圆既是轴对称图形,又是中心对称图形,故本选项符合题意;
D.等腰梯形是轴对称图形,不是中心对称图形,故本选项不符合题意.
故选:C.
6.(2分)如果存在一条直线将一个图形分割成两部分,使其中一部分图形按某个方向平移后能够与另一部分重合,那么我们把这种图形称为平移重合图形,下列图形中,不是平移重合图形的是( )
A. 正方形
B. 长方形
C. 平行四边形
D. 圆
【分析】证明平行四边形、长方形、正方形是平移重合图形即可.
【解答】解:如图,平行四边形ABCD中,取BC,AD的中点E,F,连接EF.
∵四边形ABEF向右平移可以与四边形EFDC重合,
∴平行四边形ABCD是平移重合图形,
∴长方形和正方形也是平移重合图形,
故选:D.
二、填空题(本大题共12题,每题3分,满分36分)
7.(3分)用代数式表示:“x的倒数与2021的和”是 +2021 .
【分析】用x的倒数加上2021即可.
【解答】解:根据题意可知,“x的倒数与2021的和”是+2021.
故答案为:+2021.
8.(3分)单项式﹣ab2c的系数是 ﹣ ,次数是 4 .
【分析】根据单项式的系数和次数的定义即可得出答案.
【解答】解:单项式﹣2x3的系数和次数分别﹣,4,
故答案为:﹣,4.
9.(3分)用科学记数法表示:0.00002021= 2.021×10﹣5 .
【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负整数指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
【解答】解:0.00002021=2.021×10﹣5.
故答案为:2.021×10﹣5.
10.(3分)合并同类项:2x2﹣9x2+4x2= ﹣3x2 .
【分析】利用合并同类项的法则进行计算即可.
【解答】解:原式=(2﹣9+4)x2=﹣3x2,
故答案为:﹣3x2.
11.(3分)已知一个多项式减去2x2﹣9x的结果等于x2+9x+1,那么这个多项式是 3x2+1 .
【分析】先根据题意列出算式(x2+9x+1)+(2x2﹣9x),再去括号、合并同类项即可.
【解答】解:根据题意,这个多项式为(x2+9x+1)+(2x2﹣9x)
=x2+9x+1+2x2﹣9x
=3x2+1,
故答案为:3x2+1.
12.(3分)计算:(﹣2x﹣y)2= 4x2+4xy+y2 .
【分析】根据完全平方公式化简即可.
【解答】解:原式=[﹣(2x+y)]2
=(2x+y)2
=4x2+4xy+y2,
故答案为:4x2+4xy+y2.
13.(3分)分解因式:x2﹣7x+12= (x﹣3)(x﹣4) .
【分析】因为(﹣3)×(﹣4)=12,(﹣3)+(﹣4)=﹣7,所以利用十字相乘法分解因式即可.
【解答】解:x2﹣7x+12=(x﹣3)(x﹣4).
故答案为:(x﹣3)(x﹣4).
14.(3分)对于分式,x的取值范围是 x≠1 .
【分析】根据分式的分母不为0列出不等式,解不等式即可.
【解答】解:由题意得:x﹣1≠0,
解得:x≠1,
故答案为:x≠1.
15.(3分)计算:+= .
【分析】先通分,再按照同分母分式的运算法则计算即可.
【解答】解:原式===.
故答案为:.
16.(3分)将代数式化为只含有正整数指数幂的形式,其结果是 .
【分析】根据负整数指数幂:a﹣p=(a≠0,p为正整数)进行计算即可.
【解答】解:=,
故答案为:,
17.(3分)2020年上海某垃圾处理厂5月份分别从甲乙两社区各回收干垃圾a吨,据该垃圾处理厂统计,在6月份和7月份中,甲社区干垃圾平均每月的增长率是x,乙社区干垃圾平均每月的减少率是x,那么7月份甲社区比乙社区的干垃圾量多 4ax 吨.(结果用含a、x的代数式表示)
【分析】分别表示出甲、乙社区7月份干垃圾量,相减即可得答案.
【解答】解:∵5月份分别从甲乙两社区各回收干垃圾a吨,6月份和7月份甲社区干垃圾平均每月的增长率是x,乙社区干垃圾平均每月的减少率是x,
∴7月份甲社区的干垃圾量为a(1+x)2,乙社区的干垃圾量为a(1﹣x)2,
∴7月份甲社区比乙社区的干垃圾量多a(1+x)2﹣a(1﹣x)2=a(1+2x+x2)﹣a(1﹣2x+x2)=a+2ax+ax2﹣a+2ax﹣ax2=4ax,
故答案为:4ax.
18.(3分)如图,三角形ABC是直角三角形,∠C=90°,∠B=60°,AB=6,如果将三角形ABC绕着点B旋转α(0°<α<180°),使得点A恰好落在直线BC上,点A的对应点记作点D,弧AD是点A旋转时运动的路径,那么弧AD的长是 4π或2π .(结果保留π)
【分析】分别画出图形,根据弧长计算公式及可得答案.
【解答】解:当将三角形ABC绕着点B逆时针旋转α(0°<α<180°),使得点A恰好落在直线BC上,点A的对应点记作点D,如图:
∵∠ABC=60°,
∴α=180°﹣∠ABC=120°,
∴弧AD的长是=4π,
当将三角形ABC绕着点B顺时针旋转α(0°<α<180°),使得点A恰好落在直线BC上,点A的对应点记作点D,如图:
∴弧AD的长是=2π,
综上所述,弧AD的长是4π或2π,
故答案为:4π或2π.
三、简答题(本大题共6题,每题4分,满分24分)
19.(4分)计算:(﹣2a)2 (3ab3)÷(4a2b2).
【分析】先计算单项式的乘方、将除法转化为乘法,再计算乘法即可.
【解答】解:原式=4a2 3ab3÷4a2b2
=12a3b3÷4a2b2
=3ab.
20.(4分)计算:(x+3y)(x﹣2y)﹣(2x+y)2.
【分析】根据多项式乘多项式和完全平方公式化简即可.
【解答】解:原式=x2﹣2xy+3xy﹣6y2﹣(4x2+4xy+y2)
=x2﹣2xy+3xy﹣6y2﹣4x2﹣4xy﹣y2
=﹣3x2﹣3xy﹣7y2.
21.(4分)分解因式:a2m4﹣13a2m2﹣48a2.
【分析】先提公因式,然后再利用十字相乘法,最后利用平方差公式继续分解即可.
【解答】解:a2m4﹣13a2m2﹣48a2
=a2(m4﹣13m2﹣48)
=a2(m2﹣16)(m2+3)
=a2(m+4)(m﹣4)(m2+3).
22.(4分)分解因式:a2+2ab﹣16+b2.
【分析】将a2+2ab+b2分为一组,用完全平方公式分解因式,再用平方差公式分解因式即可.
【解答】解:原式=(a2+2ab+b2)﹣16
=(a+b)2﹣42
=(a+b+4)(a+b﹣4).
23.(4分)解方程:﹣3=.
【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
【解答】解:去分母得:6﹣3(x+7)=2x,
去括号得:6﹣3x﹣21=2x,
移项合并得:﹣5x=15,
解得:x=﹣3,
经检验x=﹣3是分式方程的解.
24.(4分)计算:()﹣2×3﹣1+(π﹣2020)0÷()﹣1.
【分析】先计算负整数指数幂和零指数幂的运算,再计算乘法运算,最后算加减.
【解答】解:原式=()2×+1÷4
=×+
=1.
四、解答题(本大题共4题,第25、26题每题6分,第27、28题每题8分,满分28分)
25.(6分)如图,已知三角形ABC、直线l,点O是线段AB的中点.
(1)画出三角形ABC关于直线l的轴对称的图形;
(2)画出三角形ABC关于点O的中心对称的图形.
(不写画法,保留画图痕迹,并写出画图结论)
【分析】(1)利用轴对称的性质分别作出A,B,C的对应点A′,B′,C′即可;
(2)作出点C关于点O的对应点D,连接BD,AD,△ABD即为所求.
【解答】解:(1)如图,△A′B′C′即为所求;
(2)如图,△ABD即为所求.
26.(6分)先化简,再求值:÷﹣1,其中x=1.
【分析】先根据分式的混合运算顺序和运算法则化简原式,再将x的值代入计算即可.
【解答】解:原式= ﹣1
=﹣1
=﹣
=,
当x=1时,
原式==﹣.
27.(8分)某校为了准备“迎新活动”,用900元购买了甲、乙两种礼品共240个,其中购买甲种礼品比乙种礼品少用了180元.
(1)购买甲种礼品一共用去 360 元;(请直接写出答案)
(2)如果甲种礼品的单价是乙种礼品单价的2倍,那么乙种礼品的单价是多少元?
【分析】(1)设买甲种礼品花了x元,则买乙种礼品花了(x+180)元,由题意:用900元购买了甲、乙两种礼品,列出一元一次方程,解方程即可;
(2)设乙种礼品的单价为a元,则甲种礼品的单价为2a元,由题意:用900元购买了甲、乙两种礼品共240个,列出分式方程,解方程即可.
【解答】解:(1)设买甲种礼品花了x元,则买乙种礼品花了(x+180)元,
根据题意,得:x+x+180=900,
解得:x=360,
即买甲种礼品一共用去360元,
故答案为:360;
(2)设乙种礼品的单价为a元,则甲种礼品的单价为2a元,
根据题意,得:+=240
解得:a=3,
经检验:a=3是原分式方程的解,且符合题意,
答:乙种礼品的单价为3元.
28.(8分)如图,已知三角形ABC中,∠B=90°,将三角形ABC沿着射线BC方向平移得到三角形DEF,其中点A、点B、点C的对应点分别是点D、点E、点F,且CE=DE.
(1)如图①,如果AB=4,BC=2,那么平移的距离等于 6 ;(请直接写出答案)
(2)在第(1)题的条件下,将三角形DEF绕着点E旋转一定的角度α(0°<α<360°),使得点F恰好落在线段DE上的点G处,并联结CG、AG.请根据题意在图②中画出点G与线段CG、AG,那么旋转角α等于 90°或270° ;(请直接写出答案)
(3)在图②中,如果AB=a,BC=b,那么此时三角形ACG的面积等于 ;(用含a、b的代数式表示)
(4)在第(3)小题的情况下,如果平移的距离等于8,三角形ABC的面积等于6,那么三角形ACG的面积等于 20 ;(请直接写出答案)如果平移距离等于m,三角形ABC的面积等于n,那么三角形ACG的面积等于 ﹣2n .(用含m、n的代数式表示,请直接写出答案)
【分析】(1)由平移的性质可得△ABC≌△DEF,可得AB=DE=4=CE,即可求解;
(2)由旋转的性质直接可求解;
(3)由“SAS”可证△ABC≌△CEG,可得AC=CG,∠BAC=∠GCE,可证△ACG是等腰直角三角形,由勾股定理和三角形面积公式可求解;
(4)由完全平方公式可求BC2+AB2的值,由勾股定理和等腰直角三角形的面积公式可求解.
【解答】解:(1)∵将△ABC沿着射线BC方向平移得到△DEF,
∴△ABC≌△DEF,
∴AB=DE=4,
∵CE=DE,
∴CE=4,
∴平移距离=BC+CE=4+2=6,
故答案为:6;
(2)如图②,点G为所求点,
∴△DEF绕着点E顺时针旋转270°或△DEF绕着点E逆时针旋转90°,
故答案为:90°或270°;
(3)如图②,由折叠可知:GE=EF,
又∵AB=CE,∠ABC=∠CEG=90°,
∴△ABC≌△CEG(SAS),
∴AC=CG,∠BAC=∠GCE,
∵∠BAC+∠ACB=90°,
∴∠ACB+∠GCE=90°,
∴∠ACG=90°,
∴△ACG是等腰直角三角形,
∵AB=a,BC=b,
∴AC==,
∴S△ACG=×AC2=,
故答案为:;
(4)若平移的距离等于8,三角形ABC的面积等于6,
∴BC+CE=8,×AB×BC=6,
∵AB=CE=DE,
∴BC+AB=8,AB×BC=12,
∴BC2+AB2+2AB BC=64,
∴BC2+AB2=40,
∵AC2=BC2+AB2,
∴AC2=40,
∵△ACG是等腰直角三角形,
∴S△ACG=×AC2=20;
若平移距离等于m,三角形ABC的面积等于n,
∴BC+CE=m,×AB×BC=n,
∵AB=CE=DE,
∴BC+AB=m,AB×BC=2n,
∴BC2+AB2+2AB BC=m2,
∴BC2+AB2=m2﹣4n,
∵AC2=BC2+AB2,
∴AC2=m2﹣4n,
∵△ACG是等腰直角三角形,
∴S△ACG=×AC2=﹣2n,
故答案为:20,﹣2n.
同课章节目录
