2021-2022学年人教版九年级数学下册第27章相似 寒假自主提升专题训练 (word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册第27章相似 寒假自主提升专题训练 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 377.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-18 18:05:47 | ||
图片预览




文档简介
2021-2022学年人教版九年级数学下册《第27章相似》寒假自主提升专题训练(附答案)
1.下列图形中,为轴对称图形的是( )
A. B. C. D.
2.以下列长度的各组线段为边,能组成三角形的是( )
A.1、2、3 B.4、5、7 C.5、13、6 D.7、3、10
3.一个多边形,其每个内角都是140°,则该多边形的边数是( )
A.6 B.7 C.8 D.9
4.下列多边形中,内角和是一个三角形内角和的4倍的是( )
A.四边形 B.五边形 C.六边形 D.八边形
5.如图,直线AC、DF被三条平行线所截,若DE:EF=1:2,AB=2,则AC的值为( )
A.6 B.4 C.3 D.
6.如图,AD∥BE∥CF,直线m,n与这三条平行线分别交于点A、B、C和点D、E、F,已知AB=5,BC=10,DE=4,则EF的长为( )
A.12.5 B.12 C.8 D.4
7.如图,△ABC中,D为BC的中点,E为AC上任意一点,BE交AD于O.某同学在研究这一问题时,发现了如下事实:①当==时,有==;
②当==时,有=;
③当==时,有=;…;则当=时,=( )
B.
C. D.
8.如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,若AC=2,则AD的长是( )
A. B. C.﹣1 D.+1
9.下列每组的两个图形:两个等腰三角形;两个直角三角形;两个正方形;两个矩形;两个边长相等的菱形;两个正五边形;其中相似的有( )
A.2组 B.3组 C.4组 D.5组
10.下列线段中,能成比例的是( )
A.3cm、6cm、8cm、9cm B.3cm、5cm、6cm、9cm
C.3cm、6cm、7cm、9cm D.3cm、6cm、9cm、18cm
11.如果=,那么的值是( )
A.5 B.1 C.﹣5 D.﹣1
12.如图,Rt△ABO中,∠AOB=90°,AO=3BO,点B在反比例函数y=的图象上,OA交反比例函数y=(k≠0)的图象于点C,且OC=2CA,则k的值为( )
A.﹣2 B.﹣4 C.﹣6 D.﹣8
13.如图,在正方形ABCD中,E、F分别是CB,AB的中点,连接CF并延长,与DA的延长线交于点M,连接DE交CF于点P,连接AP,则有下列结论:①∠BCF=∠CDE;②AP=AD:③CM=CD+DE;④S△CDM=5S四边形EPFB,其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
14.如图,Rt△ABC中,AC⊥BC,AD平分∠BAC交BC于点D,DE⊥AD交AB于点E,M为AE的中点,BF⊥BC交CM的延长线于点F,BD=4,CD=3.下列结论①∠AED=∠ADC;②=;③AC BE=12;④3BF=4AC,其中结论正确的个数有( )
A.1个 B.2个 C.3个 D.4个
15.如图,△ABC是等边三角形,点D、E分别在BC、AC上,且BD=BC,CE=AC,BE、AD相交于点F,连接DE,则下列结论:①∠AFE=60°;②DE⊥AC;③CE2=DF DA;④AF BE=AE AC,正确的结论有( )
A.4个 B.3个 C.2个 D.1个
16.如图,已知 ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE、BF相交于H,BF、AD的延长线相交于G,下面结论:
①DB=BE;②∠A=∠BHE;③AB=BH;④△BHD∽△BDG.
其中正确的结论是( )
A.①②③④ B.①②③ C.①②④ D.②③④
17.如图,在平面直角坐标系中,以原点O为位似中心,将△ABO扩大到原来的2倍,得到△A′B′O.若点A的坐标是(1,2),则点A′的坐标是( )
A.(2,4) B.(﹣1,﹣2) C.(﹣2,﹣4) D.(﹣2,﹣1)
18.如图,为了测量旗杆AB的高度,小凡在距旗杆底部B点10.8米的C点处放置了一面镜子,当小凡行走到与BC位于同一直线的E点处时,恰好能从镜子中观察到旗杆顶部的A点.已知小凡眼睛所在的D点离地面的高度是1.6米,CE=2.7米,则旗杆AB的高度是( )
A.6.4米 B.7.2米 C.8米 D.9.6米
19.△ABC与△DEF相似且面积比为1:16,则△ABC与△DEF的周长比为( )
A.1:2 B.1:3 C.1:4 D.1:16
20.如图,△ABC的内角∠ABC和外角∠ACD的平分线相交于点E,BE交AC于点F,过点E作EG∥BD交AB于点G,交AC于点H,连接AE,有以下结论:
①∠BEC=∠BAC;②△HEF≌△CBF;③BG=CH+GH;④∠AEB+∠ACE=90°,其中正确的结论有 (将所有正确答案的序号填写在横线上).
21.如图,平行四边形ABCD中,E为AD的中点,已知△DEF的面积为2,则平行四边形ABCD的面积是 .
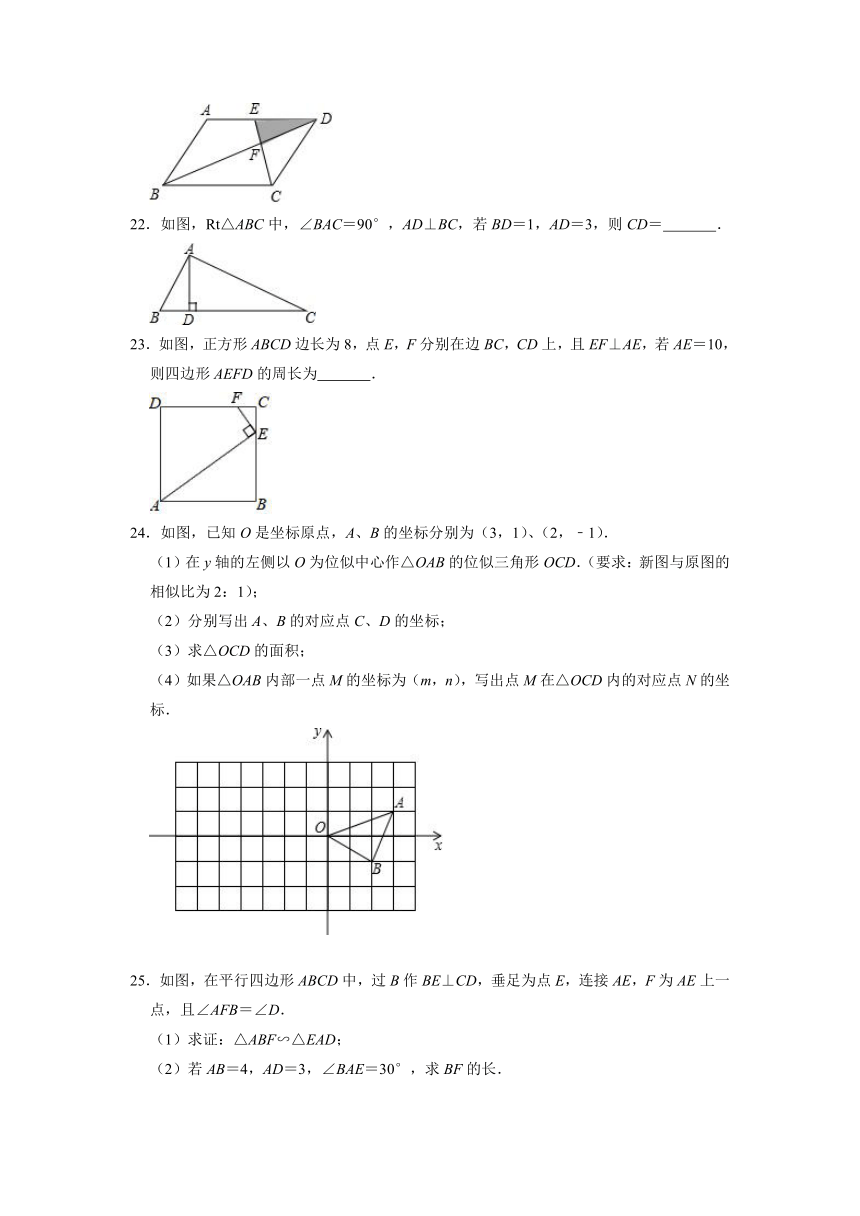
22.如图,Rt△ABC中,∠BAC=90°,AD⊥BC,若BD=1,AD=3,则CD= .
23.如图,正方形ABCD边长为8,点E,F分别在边BC,CD上,且EF⊥AE,若AE=10,则四边形AEFD的周长为 .
24.如图,已知O是坐标原点,A、B的坐标分别为(3,1)、(2,﹣1).
(1)在y轴的左侧以O为位似中心作△OAB的位似三角形OCD.(要求:新图与原图的相似比为2:1);
(2)分别写出A、B的对应点C、D的坐标;
(3)求△OCD的面积;
(4)如果△OAB内部一点M的坐标为(m,n),写出点M在△OCD内的对应点N的坐标.
25.如图,在平行四边形ABCD中,过B作BE⊥CD,垂足为点E,连接AE,F为AE上一点,且∠AFB=∠D.
(1)求证:△ABF∽△EAD;
(2)若AB=4,AD=3,∠BAE=30°,求BF的长.
26.如图,在△ABC中,DE∥BC,EF∥AB.
(1)求证:△ADE∽△EFC;
(2)若AB=7,BC=14,DE:FC=5:2,求四边形BDEF的周长.
27.如图,⊙O中,弦AB、CD相交于AB的中点E,连接AD并延长至点F,使DF=AD,连接BC、BF.
(1)求证:△CBE∽△AFB;
(2)当时,求的值.
28.如图,M为线段AB的中点,AE与BD交于点C,∠DME=∠A=∠B=α,且DM交AC于F,ME交BC于G
(1)求证:△AMF∽△BGM;
(2)连接FG,如果α=45°,AB=,BG=3,求FG的长.
29.如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:DF DE=CE CB;
(2)若AB=4,AD=3,AE=3,求AF的长.
30.如图,直立在B处的标杆AB=2.4m,直立在F处的观测者从E处看到标杆顶A、树顶C在同一条直线上(点F,B,D也在同一条直线上).已知BD=8m,FB=2.5m,人高EF=1.5m,求树高CD.
31.如图,为了测量一池塘的宽DE,在岸边找一点C,测得CD=30m,在DC的延长线上找一点A,测得AC=5m,过点A作AB∥DE,交EC的延长线于B,测得AB=6m,求池塘的宽DE.
32.已知平面直角坐标系中,△ABC的三个顶点的坐标分别为A(2,2),B(1,﹣1),C(3,0).
(1)画出以点O为位似中心,将△ABC放大到原来2倍的△A′B′C′;
(2)分别写出A′B′C′三点的坐标.
33.如图,在△ABC中,已知AB=AC=5,BC=6,点D是BC上一点,以DA为一边,点D为顶点作∠ADE=∠C,DE交线段AC于点E.
(1)求证:△ABD∽△DCE.
(2)当AE=ED时,求BD的长.
34.如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
(1)求证:AC2=AB AD;
(2)求证:CE∥AD;
(3)若AD=4,AB=6,求的值.
参考答案
1.解:A、不是轴对称图形,故本选项不符合题意;
B、不是轴对称图形,故本选项不符合题意;
C、不是轴对称图形,故本选项不符合题意;
D、是轴对称图形,故本选项符合题意.
故选:D.
2.解:A、1+2=3,不能组成三角形,故此选项错误;
B、5+4>7,能组成三角形,故此选项正确;
C、5+6<13,不能组成三角形,故此选项错误;
D、3+7=10,不能组成三角形,故此选项错误;
故选:B.
3.解:∵多边形的每个内角都等于140°,
∴多边形的每个外角都等于180°﹣140°=40°,
∴边数n=360°÷40°=9,
故选:D.
4.解:设这个多边形的边数为n.
由题意得:(n﹣2)×180°=4×180°.
解得:n=6.
答:这个多边形的边数为6.
故选:C.
5.解:∵l1∥l2∥l3,
∴,又AB=2,
∴BC=4,
∴AC=AB+BC=6.
故选:A.
6.解:∵AD∥BE∥CF,
∴=,即=,
解得,EF=8,
故选:C.
7.解:过D点作BE的平行线交AC于F,
∵D为BC的中点,∴DF是△BCE的中位线.
∵=,∴=.
∵DF是△BCE的中位线,∴F是EC的中点,∴=.
∵BE∥DF,∴==.
故选:C.
8.解:∵∠A=∠DBC=36°,∠C公共,
∴△ABC∽△BDC,
且AD=BD=BC.
设BD=x,则BC=x,CD=2﹣x.
由于=,
∴=.
整理得:x2+2x﹣4=0,
解方程得:x=﹣1±,
经检验,x=﹣1±是原方程的解,
∵x为正数,
∴x=﹣1+.
故选:C.
9.解:两个等腰三角形,其形状不确定,故不一定相似;
两个直角三角形,直角三角形中的两个锐角的大小不确定,无法判定三角形相似;
两个正方形,其边长的比值相等,对应角相等,故此图形相似;
两个矩形,其边长的比值不相等,无法判定相似;
两个边长相等的菱形,其对应角无法确定是否相等,无法判定相似;
两个正五边形,其边长的比值相等,对应角相等,故此图形相似;
故选:A.
10.解:根据如果其中两条线段的乘积等于另外两条线段的乘积,则四条线段叫成比例线段.
所给选项中,只有D符合,3×18=6×9,故选:D.
11.解:∵设==k,
∴x=2k,y=3k,
∴==﹣5,
故选:C.
12.解:如图,作CH⊥x轴于H,作BE⊥x轴于E.设B(m,n).
∵∠BOC=∠CHO=∠BEO=90°,
∴∠COH+∠HCO=90°,∠COH+∠BOE=90°,
∴∠BOE=∠COH,
∴△COH∽△OBE,
∴==,
∵AO=3OB,OC=2CA,
∴CO=2OB,
∴OH=2n,CH=2m,
∴C(﹣2n,2m),
∵mn=2,
∴k=﹣4mn=﹣8,
故选:D.
13.解:∵四边形ABCD是正方形,
∴∠DCE=∠B=90°,CD=BC=AB,
∵E、F分别是CB,AB的中点,
∴BF=AB,CE=BC,
∴BF=CE,
∴△DCE≌△CBF(SAS),
∴∠BCF=∠CDE,
故①正确;
∵∠CDE+∠CEP=90°,
∴∠BCF+∠CEP=90°,
∴∠CPE=90°,
即CF⊥DE,
∵BF=AF,∠B=∠BAM=90°,∠BFC=∠AFM,
∴△BCF≌△AMF(ASA),
∴AM=BC,
∴AD=AM,
∴AP=AD,
故②正确;
∵△DCE≌△CBF,
∴CF=DE,
∵∠FAM=90°,
∴FM>AM,
即FM>CD,
∴CM=CF+FM=DE+FM>CD+DE;
故③错误;
设CE=a,S△CDM=b,则BC=2a,AB=AD=AM=CD=2a,BF=AF=a,
∴MD=AD+AM=4a,
∴CF==a,
∵∠BCF=∠PCE,∠B=∠CPE=90°,
∴△CPE∽△CBF,
∴,
∴S△CDM=5b,
∴S四边形EPFB=4b,
∵BC∥AD,
∴△CPE∽△MPD,
∴=,
∴S△MPD=16b,
∵=,
∴S△CPD=4b,
∴S△CDM=S△CPD+S△MPD=4b+16b=20b,
∴S△CDM=5S四边形EPFB.
故④正确.
∴其中正确的结论有①②④.
故选:C.
14.解:①∠AED=90°﹣∠EAD,∠ADC=90°﹣∠DAC,
∵∠EAD=∠DAC,
∴∠AED=∠ADC.
故本选项正确;
②∵AD平分∠BAC,
∴==,
∴设AB=4x,则AC=3x,
在直角△ABC中,AC2+BC2=AB2,则(3x)2+49=(4x)2,
解得:x=,
∵∠EAD=∠DAC,∠ADE=∠ACD=90°,
∴△ADE∽△ACD,得DE:DA=DC:AC=3:3=1:,故不正确;
③由①知∠AED=∠ADC,
∴∠BED=∠BDA,
又∵∠DBE=∠ABD,
∴△BED∽△BDA,
∴DE:DA=BE:BD,由②知DE:DA=DC:AC,
∴BE:BD=DC:AC,
∴AC BE=BD DC=12.
故本选项正确;
④连接DM,
在Rt△ADE中,MD为斜边AE的中线,
则DM=MA.
∴∠MDA=∠MAD=∠DAC,
∴DM∥BF∥AC,
由DM∥BF得FM:MC=BD:DC=4:3;
由BF∥AC得△FMB∽△CMA,有BF:AC=FM:MC=4:3,
∴3BF=4AC.
故本选项正确.
综上所述,①③④正确,共有3个.
故选:C.
15.解:∵△ABC是等边三角形
∴AB=BC=AC,∠BAC=∠ABC=∠BCA=60°
∵BD=BC,CE=AC
∴BD=EC
∴△ABD≌△BCE
∴∠BAD=∠CBE,
∵∠ABE+∠EBD=60°
∴∠ABE+∠CBE=60°
∵∠AFE是△ABF的外角
∴∠AFE=60°
∴①是对的;
如图,从CD上截取CM=CE,连接EM,则△CEM是等边三角形
∴EM=CM=EC
∵EC=CD
∴EM=CM=DM
∴∠CED=90°
∴DE⊥AC,
∴②是对的;
由前面的推断知△BDF∽△ADB
∴BD:AD=DF:DB
∴BD2=DF DA
∴CE2=DF DA
∴③是对的;
在△AFE和△BAE中,∠BAE=∠AFE=60°,∠AEB是公共角
∴△AFE∽△BAE
∴AF BE=AE AC
∴④是正确的.
故选:A.
16.解:∵∠BDE=45°,DE⊥BC
∴DB=BE,BE=DE
∵DE⊥BC,BF⊥CD
∴∠BEH=∠DEC=90°
∵∠BHE=∠DHF
∴∠EBH=∠CDE
∴△BEH≌△DEC
∴∠BHE=∠C,BH=CD
∵ ABCD中
∴∠C=∠A,AB=CD
∴∠A=∠BHE,AB=BH
∴正确的有①②③
故选:B.
17.解:根据以原点O为位似中心,图形的坐标特点得出,对应点的坐标应乘以﹣2,
故点A的坐标是(1,2),则点A′的坐标是(﹣2,﹣4),
故选:C.
18.解:过点C作镜面的法线CH,由光学原理得∠DCH=∠ACH,
∵∠DCE=90°﹣∠DCH,
∠ACB=90°﹣∠ACH,
∴∠DCE=∠ACB,
又∵∠DEC=∠ABC=90°,
∴△CDE∽△CAB,
∴=,
即=,
解得AB=6.4(m).
答:旗杆AB高为6.4米.
故选:A.
19.解:∵相似三角形△ABC与△DEF面积的比为1:16,
∴它们的相似比为1:4,
∴△ABC与△DEF的周长比为1:4.
故选:C.
20.解:①BE平分∠ABC,
∴∠EBC=∠ABC,
∵CE平分∠ACD,
∴∠DCE=ACD,
∵∠ACD=∠BAC+∠ABC,∠DCE=∠CBE+∠BEC,
∴∠EBC+∠BEC=(∠BAC+∠ABC)=∠EBC+BAC,
∴∠BEC=∠BAC,故①正确;
∵②△HEF与△CBF只有两个角是相等的,能得出相似,但不含相等的边,所有不能得出全等的结论,故②错误.
③BE平分∠ABC,
∴∠ABE=∠CBE,
∵GE∥BC,
∴∠CBE=∠GEB,
∴∠ABE=∠GEB,
∴BG=GE,
同理CH=HE,
∴BG﹣CH=GE﹣EH=GH,
故③正确.
④过点E作EN⊥AC于N,ED⊥BC于D,EM⊥BA于M,如图,
∵BE平分∠ABC,
∴EM=ED,
∵CE平分∠ACD,
∴EN=ED,
∴EN=EM,
∴AE平分∠CAM,
设∠ACE=∠DCE=x,∠ABE=∠CBE=y,∠MAE=∠CAE=z,如图,
则∠BAC=180°﹣2z,∠ACB=180﹣2x,
∵∠ABC+∠ACB+∠BAC=180°,
∴2y+180°﹣2z+180°﹣2x=180°,
∴x+z=y+90°,
∵z=y+∠AEB,
∴x+y+∠AEB=y+90°,
∴x+∠AEB=90°,
即∠ACE+∠AEB=90°,故④正确;
故答案为:①③④.
21.解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴△DEF∽△BCF,
∴S△DEF:S△BCF=()2,
又∵E是AD中点,
∴DE=AD=BC,
∴DE:BC=DF:BF=1:2,
∴S△DEF:S△BCF=1:4,
∴S△BCF=8,
又∵DF:BF=1:2,
∴S△DCF=4,
∴S ABCD=2(S△DCF+S△BCF)=24.
故答案为:24.
22.解:∵Rt△ABC中,∠BAC=90°,
∴∠B+∠C=90°.
∵AD⊥BC于点D,
∴∠B+∠BAD=90°,∠C+∠CAD=90°,
∴∠BAD=∠C,∠B=∠CAD,
∴△ABD∽△CAD,
∴AD2=BD CD,
∵BD=1,AD=3,
∴CD=9,
故答案为:9
23.解:在正方形ABCD中,
AE=10,AB=8,
∴由勾股定理可知:BE=6,
∴CE=8﹣6=2
∵∠AEB+∠FEC=90°,
∠AEB+∠EAB=90°
∴∠FEC=∠EAB
∴△AEB∽△EFC
∴=
∴,
∴CF=,
∴DF=8﹣=
由勾股定理可知:EF=,
∴四边形AEFD的周长为:8+10++=27
故答案为:27
24.解:(1)如图:
(2)C(﹣6,﹣2),D(﹣4,2);
(3)如图所示:
∵DE=4,OE=2,OF=2,EF=4,CF=6,
∴S△OCD=S梯形CDEF﹣S△ODE﹣S△OCF=(DE+CF) EF﹣DE OE﹣CF OF,
=×(4+6)×4﹣×4×2﹣×6×2,
=10;
(4)∵△OAB内部一点M的坐标为(m,n),
∴点M在△OCD内的对应点N的坐标为(﹣2m,﹣2n).
25.(1)证明:∵在平行四边形ABCD中,AB∥CD,
∴∠BAF=∠AED.
又∠AFB=∠D,
∴△ABF∽△EAD;
(2)解:∵BE⊥CD,AB∥CD,
∴BE⊥AB.
∴∠ABE=90°.
又∠BAE=30°,AB=4,
∴AE===
∵由(1)知,△ABF∽△EAD,
∴=.即=,
∴BF=.
26.解:(1)∵DE∥BC,EF∥AB,
∴∠AED=∠C,∠EFC=∠B,∠ADE=∠B,
∴∠ADE=∠EFC,
∴△ADE∽△EFC;
(2)∵DE∥BC,EF∥AB,
∴四边形BDEF是平行四边形,
∴DE=BF,BD=EF,
∵△ADE∽△EFC,
∴==,
∴=,=,
∵AB=7,BC=14,
∴BD=2,BF=10,
∴四边形BDEF的周长=2(2+10)=24.
27.(1)证明:∵AE=EB,AD=DF,
∴ED是△ABF的中位线,
∴ED∥BF,
∴∠CEB=∠ABF,
又∠C=∠A,
∴△CBE∽△AFB.
(2)解:由(1)知,△CBE∽△AFB,
∴,
又AF=2AD,
∴.
28.(1)证明:∵∠DME=∠A=∠B=α,
∴∠AMF+∠BMG=180°﹣α,
∵∠A+∠AMF+∠AFM=180°,
∴∠AMF+∠AFM=180°﹣α,
∴∠AFM=∠BMG,
∴△AMF∽△BGM;
(2)解:当α=45°时,可得AC⊥BC且AC=BC,
∵M为AB的中点,
∴AM=BM=2,
∵△AMF∽△BGM,
∴,
∴AF===,AC=BC=4 cos45°=4,
∴CF=AC﹣AF=4﹣=,CG=BC﹣BG=4﹣3=1,
∴FG===.
29.(1)证明:∵平行四边形ABCD,∠AFE=∠B,
∴AB∥CD,AD∥BC,AD=BC,
∴∠B+∠C=180°,∠ADF=∠CED,
∵∠AFD+∠AFE=180°,
∴∠C=∠AFD,
∴△ADF∽△DEC,
∴=,即DF DE=CE AD,
则DF DE=CE CB;
(2)解:∵AE⊥BC,
∴∠AEB=∠AEC=90°,
在Rt△ADE中,根据勾股定理得:DE==3,
∵△ADF∽△DEC,
∴=,即=,
解得:AF=2.
30.解:过E作EH⊥CD交CD于H点,交AB于点G,如下图所示:
由已知得,EF⊥FD,AB⊥FD,CD⊥FD,
∵EH⊥CD,EH⊥AB,
∴四边形EFDH为矩形,
∴EF=GB=DH=1.5米,EG=FB=2.5米,GH=BD=8米,
∴AG=AB﹣GB=2.4﹣1.5=0.9米,
∵EH⊥CD,EH⊥AB,
∴AG∥CH,
∴△AEG∽△CEH,
∴=,
∴=,
解得:CH=3.78米,
∴DC=CH+DH=3.78+1.5=5.28米.
答:故树高DC为5.28米.
31.解:∵AB∥DE,CD=30m,AC=5m,AB=6m,
∴△ABC∽△DEC.
∴AC:CD=AB:ED,
∴5:30=6:ED,
解得,ED=36m,
答:池塘的宽DE是36m.
32.解:(1)如图所示:△A′B′C′和△A″B″C″即为所求;
(2)如图所示:A′(4,4),B′(2,﹣2),C′(6,0);
A″(﹣4,﹣4),B″(﹣2,2),C″(﹣6,0).
33.(1)证明:∵AB=AC,
∴∠B=∠C,
又∵∠ADE+∠CDE=∠B+∠BAD,
∴∠BAD=∠CDE,
∴△ABD∽△DCE;
(2)解:∵△ABD∽△DCE,
∴=,
即=,
∵AE=ED,
∴∠ADE=∠DAE,
∵∠ADE=∠C,
∴∠ADE=∠DAE=∠B=∠C,
∴△ABC∽△EAD,
∴=,
即=,
∴=,
∴=,
解得CD=,
BD=BC﹣CD=6﹣=.
34.(1)证明:∵AC平分∠DAB,
∴∠DAC=∠CAB,
∵∠ADC=∠ACB=90°,
∴△ADC∽△ACB,
∴AD:AC=AC:AB,
∴AC2=AB AD;
(2)证明:∵E为AB的中点,
∴CE=AB=AE,
∴∠EAC=∠ECA,
∵∠DAC=∠CAB,
∴∠DAC=∠ECA,
∴CE∥AD;
(3)解:∵CE∥AD,
∴△AFD∽△CFE,
∴AD:CE=AF:CF,
∵CE=AB,
∴CE=×6=3,
∵AD=4,
∴,
∴.
1.下列图形中,为轴对称图形的是( )
A. B. C. D.
2.以下列长度的各组线段为边,能组成三角形的是( )
A.1、2、3 B.4、5、7 C.5、13、6 D.7、3、10
3.一个多边形,其每个内角都是140°,则该多边形的边数是( )
A.6 B.7 C.8 D.9
4.下列多边形中,内角和是一个三角形内角和的4倍的是( )
A.四边形 B.五边形 C.六边形 D.八边形
5.如图,直线AC、DF被三条平行线所截,若DE:EF=1:2,AB=2,则AC的值为( )
A.6 B.4 C.3 D.
6.如图,AD∥BE∥CF,直线m,n与这三条平行线分别交于点A、B、C和点D、E、F,已知AB=5,BC=10,DE=4,则EF的长为( )
A.12.5 B.12 C.8 D.4
7.如图,△ABC中,D为BC的中点,E为AC上任意一点,BE交AD于O.某同学在研究这一问题时,发现了如下事实:①当==时,有==;
②当==时,有=;
③当==时,有=;…;则当=时,=( )
B.
C. D.
8.如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,若AC=2,则AD的长是( )
A. B. C.﹣1 D.+1
9.下列每组的两个图形:两个等腰三角形;两个直角三角形;两个正方形;两个矩形;两个边长相等的菱形;两个正五边形;其中相似的有( )
A.2组 B.3组 C.4组 D.5组
10.下列线段中,能成比例的是( )
A.3cm、6cm、8cm、9cm B.3cm、5cm、6cm、9cm
C.3cm、6cm、7cm、9cm D.3cm、6cm、9cm、18cm
11.如果=,那么的值是( )
A.5 B.1 C.﹣5 D.﹣1
12.如图,Rt△ABO中,∠AOB=90°,AO=3BO,点B在反比例函数y=的图象上,OA交反比例函数y=(k≠0)的图象于点C,且OC=2CA,则k的值为( )
A.﹣2 B.﹣4 C.﹣6 D.﹣8
13.如图,在正方形ABCD中,E、F分别是CB,AB的中点,连接CF并延长,与DA的延长线交于点M,连接DE交CF于点P,连接AP,则有下列结论:①∠BCF=∠CDE;②AP=AD:③CM=CD+DE;④S△CDM=5S四边形EPFB,其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
14.如图,Rt△ABC中,AC⊥BC,AD平分∠BAC交BC于点D,DE⊥AD交AB于点E,M为AE的中点,BF⊥BC交CM的延长线于点F,BD=4,CD=3.下列结论①∠AED=∠ADC;②=;③AC BE=12;④3BF=4AC,其中结论正确的个数有( )
A.1个 B.2个 C.3个 D.4个
15.如图,△ABC是等边三角形,点D、E分别在BC、AC上,且BD=BC,CE=AC,BE、AD相交于点F,连接DE,则下列结论:①∠AFE=60°;②DE⊥AC;③CE2=DF DA;④AF BE=AE AC,正确的结论有( )
A.4个 B.3个 C.2个 D.1个
16.如图,已知 ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE、BF相交于H,BF、AD的延长线相交于G,下面结论:
①DB=BE;②∠A=∠BHE;③AB=BH;④△BHD∽△BDG.
其中正确的结论是( )
A.①②③④ B.①②③ C.①②④ D.②③④
17.如图,在平面直角坐标系中,以原点O为位似中心,将△ABO扩大到原来的2倍,得到△A′B′O.若点A的坐标是(1,2),则点A′的坐标是( )
A.(2,4) B.(﹣1,﹣2) C.(﹣2,﹣4) D.(﹣2,﹣1)
18.如图,为了测量旗杆AB的高度,小凡在距旗杆底部B点10.8米的C点处放置了一面镜子,当小凡行走到与BC位于同一直线的E点处时,恰好能从镜子中观察到旗杆顶部的A点.已知小凡眼睛所在的D点离地面的高度是1.6米,CE=2.7米,则旗杆AB的高度是( )
A.6.4米 B.7.2米 C.8米 D.9.6米
19.△ABC与△DEF相似且面积比为1:16,则△ABC与△DEF的周长比为( )
A.1:2 B.1:3 C.1:4 D.1:16
20.如图,△ABC的内角∠ABC和外角∠ACD的平分线相交于点E,BE交AC于点F,过点E作EG∥BD交AB于点G,交AC于点H,连接AE,有以下结论:
①∠BEC=∠BAC;②△HEF≌△CBF;③BG=CH+GH;④∠AEB+∠ACE=90°,其中正确的结论有 (将所有正确答案的序号填写在横线上).
21.如图,平行四边形ABCD中,E为AD的中点,已知△DEF的面积为2,则平行四边形ABCD的面积是 .
22.如图,Rt△ABC中,∠BAC=90°,AD⊥BC,若BD=1,AD=3,则CD= .
23.如图,正方形ABCD边长为8,点E,F分别在边BC,CD上,且EF⊥AE,若AE=10,则四边形AEFD的周长为 .
24.如图,已知O是坐标原点,A、B的坐标分别为(3,1)、(2,﹣1).
(1)在y轴的左侧以O为位似中心作△OAB的位似三角形OCD.(要求:新图与原图的相似比为2:1);
(2)分别写出A、B的对应点C、D的坐标;
(3)求△OCD的面积;
(4)如果△OAB内部一点M的坐标为(m,n),写出点M在△OCD内的对应点N的坐标.
25.如图,在平行四边形ABCD中,过B作BE⊥CD,垂足为点E,连接AE,F为AE上一点,且∠AFB=∠D.
(1)求证:△ABF∽△EAD;
(2)若AB=4,AD=3,∠BAE=30°,求BF的长.
26.如图,在△ABC中,DE∥BC,EF∥AB.
(1)求证:△ADE∽△EFC;
(2)若AB=7,BC=14,DE:FC=5:2,求四边形BDEF的周长.
27.如图,⊙O中,弦AB、CD相交于AB的中点E,连接AD并延长至点F,使DF=AD,连接BC、BF.
(1)求证:△CBE∽△AFB;
(2)当时,求的值.
28.如图,M为线段AB的中点,AE与BD交于点C,∠DME=∠A=∠B=α,且DM交AC于F,ME交BC于G
(1)求证:△AMF∽△BGM;
(2)连接FG,如果α=45°,AB=,BG=3,求FG的长.
29.如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:DF DE=CE CB;
(2)若AB=4,AD=3,AE=3,求AF的长.
30.如图,直立在B处的标杆AB=2.4m,直立在F处的观测者从E处看到标杆顶A、树顶C在同一条直线上(点F,B,D也在同一条直线上).已知BD=8m,FB=2.5m,人高EF=1.5m,求树高CD.
31.如图,为了测量一池塘的宽DE,在岸边找一点C,测得CD=30m,在DC的延长线上找一点A,测得AC=5m,过点A作AB∥DE,交EC的延长线于B,测得AB=6m,求池塘的宽DE.
32.已知平面直角坐标系中,△ABC的三个顶点的坐标分别为A(2,2),B(1,﹣1),C(3,0).
(1)画出以点O为位似中心,将△ABC放大到原来2倍的△A′B′C′;
(2)分别写出A′B′C′三点的坐标.
33.如图,在△ABC中,已知AB=AC=5,BC=6,点D是BC上一点,以DA为一边,点D为顶点作∠ADE=∠C,DE交线段AC于点E.
(1)求证:△ABD∽△DCE.
(2)当AE=ED时,求BD的长.
34.如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
(1)求证:AC2=AB AD;
(2)求证:CE∥AD;
(3)若AD=4,AB=6,求的值.
参考答案
1.解:A、不是轴对称图形,故本选项不符合题意;
B、不是轴对称图形,故本选项不符合题意;
C、不是轴对称图形,故本选项不符合题意;
D、是轴对称图形,故本选项符合题意.
故选:D.
2.解:A、1+2=3,不能组成三角形,故此选项错误;
B、5+4>7,能组成三角形,故此选项正确;
C、5+6<13,不能组成三角形,故此选项错误;
D、3+7=10,不能组成三角形,故此选项错误;
故选:B.
3.解:∵多边形的每个内角都等于140°,
∴多边形的每个外角都等于180°﹣140°=40°,
∴边数n=360°÷40°=9,
故选:D.
4.解:设这个多边形的边数为n.
由题意得:(n﹣2)×180°=4×180°.
解得:n=6.
答:这个多边形的边数为6.
故选:C.
5.解:∵l1∥l2∥l3,
∴,又AB=2,
∴BC=4,
∴AC=AB+BC=6.
故选:A.
6.解:∵AD∥BE∥CF,
∴=,即=,
解得,EF=8,
故选:C.
7.解:过D点作BE的平行线交AC于F,
∵D为BC的中点,∴DF是△BCE的中位线.
∵=,∴=.
∵DF是△BCE的中位线,∴F是EC的中点,∴=.
∵BE∥DF,∴==.
故选:C.
8.解:∵∠A=∠DBC=36°,∠C公共,
∴△ABC∽△BDC,
且AD=BD=BC.
设BD=x,则BC=x,CD=2﹣x.
由于=,
∴=.
整理得:x2+2x﹣4=0,
解方程得:x=﹣1±,
经检验,x=﹣1±是原方程的解,
∵x为正数,
∴x=﹣1+.
故选:C.
9.解:两个等腰三角形,其形状不确定,故不一定相似;
两个直角三角形,直角三角形中的两个锐角的大小不确定,无法判定三角形相似;
两个正方形,其边长的比值相等,对应角相等,故此图形相似;
两个矩形,其边长的比值不相等,无法判定相似;
两个边长相等的菱形,其对应角无法确定是否相等,无法判定相似;
两个正五边形,其边长的比值相等,对应角相等,故此图形相似;
故选:A.
10.解:根据如果其中两条线段的乘积等于另外两条线段的乘积,则四条线段叫成比例线段.
所给选项中,只有D符合,3×18=6×9,故选:D.
11.解:∵设==k,
∴x=2k,y=3k,
∴==﹣5,
故选:C.
12.解:如图,作CH⊥x轴于H,作BE⊥x轴于E.设B(m,n).
∵∠BOC=∠CHO=∠BEO=90°,
∴∠COH+∠HCO=90°,∠COH+∠BOE=90°,
∴∠BOE=∠COH,
∴△COH∽△OBE,
∴==,
∵AO=3OB,OC=2CA,
∴CO=2OB,
∴OH=2n,CH=2m,
∴C(﹣2n,2m),
∵mn=2,
∴k=﹣4mn=﹣8,
故选:D.
13.解:∵四边形ABCD是正方形,
∴∠DCE=∠B=90°,CD=BC=AB,
∵E、F分别是CB,AB的中点,
∴BF=AB,CE=BC,
∴BF=CE,
∴△DCE≌△CBF(SAS),
∴∠BCF=∠CDE,
故①正确;
∵∠CDE+∠CEP=90°,
∴∠BCF+∠CEP=90°,
∴∠CPE=90°,
即CF⊥DE,
∵BF=AF,∠B=∠BAM=90°,∠BFC=∠AFM,
∴△BCF≌△AMF(ASA),
∴AM=BC,
∴AD=AM,
∴AP=AD,
故②正确;
∵△DCE≌△CBF,
∴CF=DE,
∵∠FAM=90°,
∴FM>AM,
即FM>CD,
∴CM=CF+FM=DE+FM>CD+DE;
故③错误;
设CE=a,S△CDM=b,则BC=2a,AB=AD=AM=CD=2a,BF=AF=a,
∴MD=AD+AM=4a,
∴CF==a,
∵∠BCF=∠PCE,∠B=∠CPE=90°,
∴△CPE∽△CBF,
∴,
∴S△CDM=5b,
∴S四边形EPFB=4b,
∵BC∥AD,
∴△CPE∽△MPD,
∴=,
∴S△MPD=16b,
∵=,
∴S△CPD=4b,
∴S△CDM=S△CPD+S△MPD=4b+16b=20b,
∴S△CDM=5S四边形EPFB.
故④正确.
∴其中正确的结论有①②④.
故选:C.
14.解:①∠AED=90°﹣∠EAD,∠ADC=90°﹣∠DAC,
∵∠EAD=∠DAC,
∴∠AED=∠ADC.
故本选项正确;
②∵AD平分∠BAC,
∴==,
∴设AB=4x,则AC=3x,
在直角△ABC中,AC2+BC2=AB2,则(3x)2+49=(4x)2,
解得:x=,
∵∠EAD=∠DAC,∠ADE=∠ACD=90°,
∴△ADE∽△ACD,得DE:DA=DC:AC=3:3=1:,故不正确;
③由①知∠AED=∠ADC,
∴∠BED=∠BDA,
又∵∠DBE=∠ABD,
∴△BED∽△BDA,
∴DE:DA=BE:BD,由②知DE:DA=DC:AC,
∴BE:BD=DC:AC,
∴AC BE=BD DC=12.
故本选项正确;
④连接DM,
在Rt△ADE中,MD为斜边AE的中线,
则DM=MA.
∴∠MDA=∠MAD=∠DAC,
∴DM∥BF∥AC,
由DM∥BF得FM:MC=BD:DC=4:3;
由BF∥AC得△FMB∽△CMA,有BF:AC=FM:MC=4:3,
∴3BF=4AC.
故本选项正确.
综上所述,①③④正确,共有3个.
故选:C.
15.解:∵△ABC是等边三角形
∴AB=BC=AC,∠BAC=∠ABC=∠BCA=60°
∵BD=BC,CE=AC
∴BD=EC
∴△ABD≌△BCE
∴∠BAD=∠CBE,
∵∠ABE+∠EBD=60°
∴∠ABE+∠CBE=60°
∵∠AFE是△ABF的外角
∴∠AFE=60°
∴①是对的;
如图,从CD上截取CM=CE,连接EM,则△CEM是等边三角形
∴EM=CM=EC
∵EC=CD
∴EM=CM=DM
∴∠CED=90°
∴DE⊥AC,
∴②是对的;
由前面的推断知△BDF∽△ADB
∴BD:AD=DF:DB
∴BD2=DF DA
∴CE2=DF DA
∴③是对的;
在△AFE和△BAE中,∠BAE=∠AFE=60°,∠AEB是公共角
∴△AFE∽△BAE
∴AF BE=AE AC
∴④是正确的.
故选:A.
16.解:∵∠BDE=45°,DE⊥BC
∴DB=BE,BE=DE
∵DE⊥BC,BF⊥CD
∴∠BEH=∠DEC=90°
∵∠BHE=∠DHF
∴∠EBH=∠CDE
∴△BEH≌△DEC
∴∠BHE=∠C,BH=CD
∵ ABCD中
∴∠C=∠A,AB=CD
∴∠A=∠BHE,AB=BH
∴正确的有①②③
故选:B.
17.解:根据以原点O为位似中心,图形的坐标特点得出,对应点的坐标应乘以﹣2,
故点A的坐标是(1,2),则点A′的坐标是(﹣2,﹣4),
故选:C.
18.解:过点C作镜面的法线CH,由光学原理得∠DCH=∠ACH,
∵∠DCE=90°﹣∠DCH,
∠ACB=90°﹣∠ACH,
∴∠DCE=∠ACB,
又∵∠DEC=∠ABC=90°,
∴△CDE∽△CAB,
∴=,
即=,
解得AB=6.4(m).
答:旗杆AB高为6.4米.
故选:A.
19.解:∵相似三角形△ABC与△DEF面积的比为1:16,
∴它们的相似比为1:4,
∴△ABC与△DEF的周长比为1:4.
故选:C.
20.解:①BE平分∠ABC,
∴∠EBC=∠ABC,
∵CE平分∠ACD,
∴∠DCE=ACD,
∵∠ACD=∠BAC+∠ABC,∠DCE=∠CBE+∠BEC,
∴∠EBC+∠BEC=(∠BAC+∠ABC)=∠EBC+BAC,
∴∠BEC=∠BAC,故①正确;
∵②△HEF与△CBF只有两个角是相等的,能得出相似,但不含相等的边,所有不能得出全等的结论,故②错误.
③BE平分∠ABC,
∴∠ABE=∠CBE,
∵GE∥BC,
∴∠CBE=∠GEB,
∴∠ABE=∠GEB,
∴BG=GE,
同理CH=HE,
∴BG﹣CH=GE﹣EH=GH,
故③正确.
④过点E作EN⊥AC于N,ED⊥BC于D,EM⊥BA于M,如图,
∵BE平分∠ABC,
∴EM=ED,
∵CE平分∠ACD,
∴EN=ED,
∴EN=EM,
∴AE平分∠CAM,
设∠ACE=∠DCE=x,∠ABE=∠CBE=y,∠MAE=∠CAE=z,如图,
则∠BAC=180°﹣2z,∠ACB=180﹣2x,
∵∠ABC+∠ACB+∠BAC=180°,
∴2y+180°﹣2z+180°﹣2x=180°,
∴x+z=y+90°,
∵z=y+∠AEB,
∴x+y+∠AEB=y+90°,
∴x+∠AEB=90°,
即∠ACE+∠AEB=90°,故④正确;
故答案为:①③④.
21.解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴△DEF∽△BCF,
∴S△DEF:S△BCF=()2,
又∵E是AD中点,
∴DE=AD=BC,
∴DE:BC=DF:BF=1:2,
∴S△DEF:S△BCF=1:4,
∴S△BCF=8,
又∵DF:BF=1:2,
∴S△DCF=4,
∴S ABCD=2(S△DCF+S△BCF)=24.
故答案为:24.
22.解:∵Rt△ABC中,∠BAC=90°,
∴∠B+∠C=90°.
∵AD⊥BC于点D,
∴∠B+∠BAD=90°,∠C+∠CAD=90°,
∴∠BAD=∠C,∠B=∠CAD,
∴△ABD∽△CAD,
∴AD2=BD CD,
∵BD=1,AD=3,
∴CD=9,
故答案为:9
23.解:在正方形ABCD中,
AE=10,AB=8,
∴由勾股定理可知:BE=6,
∴CE=8﹣6=2
∵∠AEB+∠FEC=90°,
∠AEB+∠EAB=90°
∴∠FEC=∠EAB
∴△AEB∽△EFC
∴=
∴,
∴CF=,
∴DF=8﹣=
由勾股定理可知:EF=,
∴四边形AEFD的周长为:8+10++=27
故答案为:27
24.解:(1)如图:
(2)C(﹣6,﹣2),D(﹣4,2);
(3)如图所示:
∵DE=4,OE=2,OF=2,EF=4,CF=6,
∴S△OCD=S梯形CDEF﹣S△ODE﹣S△OCF=(DE+CF) EF﹣DE OE﹣CF OF,
=×(4+6)×4﹣×4×2﹣×6×2,
=10;
(4)∵△OAB内部一点M的坐标为(m,n),
∴点M在△OCD内的对应点N的坐标为(﹣2m,﹣2n).
25.(1)证明:∵在平行四边形ABCD中,AB∥CD,
∴∠BAF=∠AED.
又∠AFB=∠D,
∴△ABF∽△EAD;
(2)解:∵BE⊥CD,AB∥CD,
∴BE⊥AB.
∴∠ABE=90°.
又∠BAE=30°,AB=4,
∴AE===
∵由(1)知,△ABF∽△EAD,
∴=.即=,
∴BF=.
26.解:(1)∵DE∥BC,EF∥AB,
∴∠AED=∠C,∠EFC=∠B,∠ADE=∠B,
∴∠ADE=∠EFC,
∴△ADE∽△EFC;
(2)∵DE∥BC,EF∥AB,
∴四边形BDEF是平行四边形,
∴DE=BF,BD=EF,
∵△ADE∽△EFC,
∴==,
∴=,=,
∵AB=7,BC=14,
∴BD=2,BF=10,
∴四边形BDEF的周长=2(2+10)=24.
27.(1)证明:∵AE=EB,AD=DF,
∴ED是△ABF的中位线,
∴ED∥BF,
∴∠CEB=∠ABF,
又∠C=∠A,
∴△CBE∽△AFB.
(2)解:由(1)知,△CBE∽△AFB,
∴,
又AF=2AD,
∴.
28.(1)证明:∵∠DME=∠A=∠B=α,
∴∠AMF+∠BMG=180°﹣α,
∵∠A+∠AMF+∠AFM=180°,
∴∠AMF+∠AFM=180°﹣α,
∴∠AFM=∠BMG,
∴△AMF∽△BGM;
(2)解:当α=45°时,可得AC⊥BC且AC=BC,
∵M为AB的中点,
∴AM=BM=2,
∵△AMF∽△BGM,
∴,
∴AF===,AC=BC=4 cos45°=4,
∴CF=AC﹣AF=4﹣=,CG=BC﹣BG=4﹣3=1,
∴FG===.
29.(1)证明:∵平行四边形ABCD,∠AFE=∠B,
∴AB∥CD,AD∥BC,AD=BC,
∴∠B+∠C=180°,∠ADF=∠CED,
∵∠AFD+∠AFE=180°,
∴∠C=∠AFD,
∴△ADF∽△DEC,
∴=,即DF DE=CE AD,
则DF DE=CE CB;
(2)解:∵AE⊥BC,
∴∠AEB=∠AEC=90°,
在Rt△ADE中,根据勾股定理得:DE==3,
∵△ADF∽△DEC,
∴=,即=,
解得:AF=2.
30.解:过E作EH⊥CD交CD于H点,交AB于点G,如下图所示:
由已知得,EF⊥FD,AB⊥FD,CD⊥FD,
∵EH⊥CD,EH⊥AB,
∴四边形EFDH为矩形,
∴EF=GB=DH=1.5米,EG=FB=2.5米,GH=BD=8米,
∴AG=AB﹣GB=2.4﹣1.5=0.9米,
∵EH⊥CD,EH⊥AB,
∴AG∥CH,
∴△AEG∽△CEH,
∴=,
∴=,
解得:CH=3.78米,
∴DC=CH+DH=3.78+1.5=5.28米.
答:故树高DC为5.28米.
31.解:∵AB∥DE,CD=30m,AC=5m,AB=6m,
∴△ABC∽△DEC.
∴AC:CD=AB:ED,
∴5:30=6:ED,
解得,ED=36m,
答:池塘的宽DE是36m.
32.解:(1)如图所示:△A′B′C′和△A″B″C″即为所求;
(2)如图所示:A′(4,4),B′(2,﹣2),C′(6,0);
A″(﹣4,﹣4),B″(﹣2,2),C″(﹣6,0).
33.(1)证明:∵AB=AC,
∴∠B=∠C,
又∵∠ADE+∠CDE=∠B+∠BAD,
∴∠BAD=∠CDE,
∴△ABD∽△DCE;
(2)解:∵△ABD∽△DCE,
∴=,
即=,
∵AE=ED,
∴∠ADE=∠DAE,
∵∠ADE=∠C,
∴∠ADE=∠DAE=∠B=∠C,
∴△ABC∽△EAD,
∴=,
即=,
∴=,
∴=,
解得CD=,
BD=BC﹣CD=6﹣=.
34.(1)证明:∵AC平分∠DAB,
∴∠DAC=∠CAB,
∵∠ADC=∠ACB=90°,
∴△ADC∽△ACB,
∴AD:AC=AC:AB,
∴AC2=AB AD;
(2)证明:∵E为AB的中点,
∴CE=AB=AE,
∴∠EAC=∠ECA,
∵∠DAC=∠CAB,
∴∠DAC=∠ECA,
∴CE∥AD;
(3)解:∵CE∥AD,
∴△AFD∽△CFE,
∴AD:CE=AF:CF,
∵CE=AB,
∴CE=×6=3,
∵AD=4,
∴,
∴.
