四川省乐山市2021-2022学年高一上学期期末考试数学试题(Word版含答案解析)
文档属性
| 名称 | 四川省乐山市2021-2022学年高一上学期期末考试数学试题(Word版含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 446.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-18 12:29:45 | ||
图片预览



文档简介
乐山市2021-2022学年高一上学期期末考试
数学
第一部分(选择题 共60分)
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合,,则( ).
A. B. C. D.
2.( ).
A. B. C. D.
3.巳知集合,,有以下结论:①;②;③.其中错误的是( ).
A.①③ B.②③ C.①② D.①②③
4.( ).
A. B. C. D.1
5.已知为奇函数,当时,,则( ).
A.3 B. C.1 D.
6.巳知,,则( ).
A. B. C. D.
7.当前,全球疫情仍处于大流行状态,多国放松管控给我国外防输入带来挑战,冬季季节因素导致周边国家疫情输入我国风险大大增加.现有一组境外输人病例数据:
x(月份) 1 2 3 4 5
y(人数) 97 159 198 235 261
则x,y的函数关系与下列哪类函数最接近( ).
A. B.
C. D.
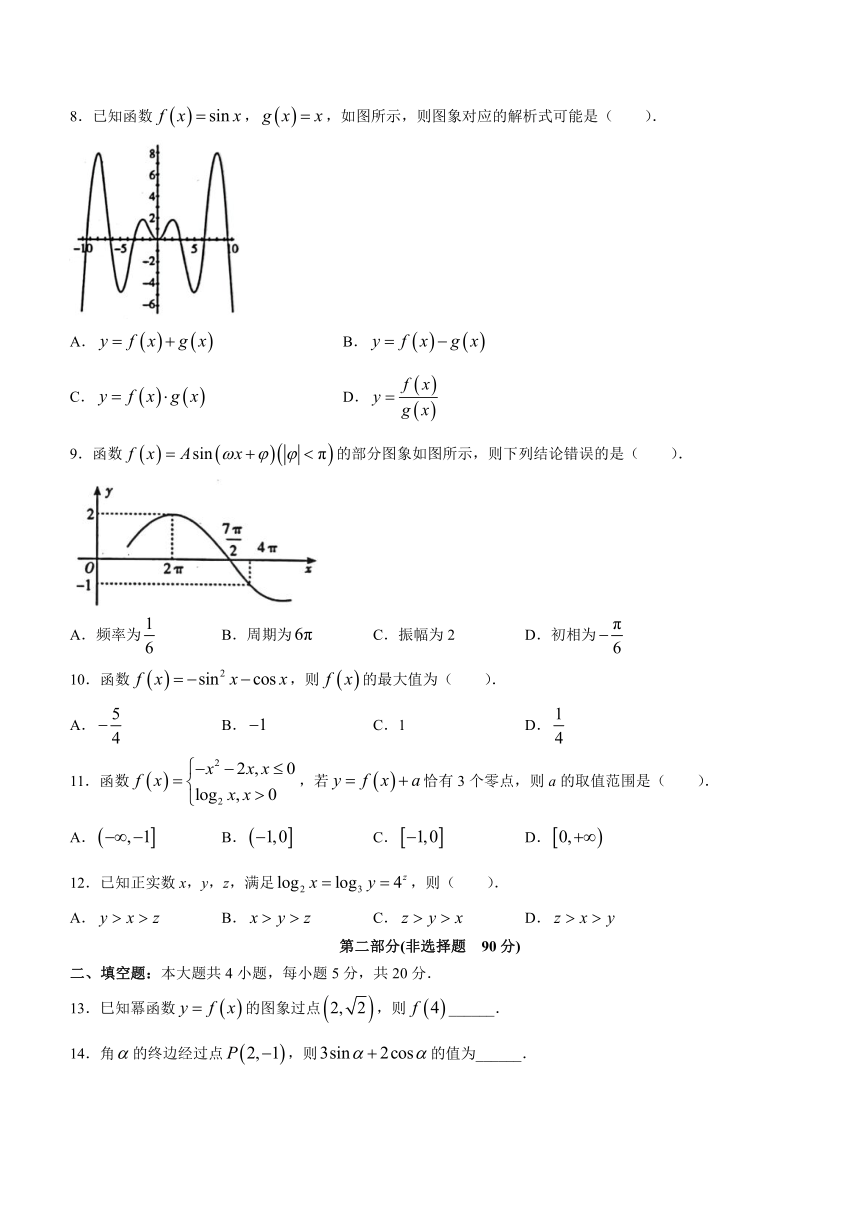
8.已知函数,,如图所示,则图象对应的解析式可能是( ).
A. B.
C. D.
9.函数的部分图象如图所示,则下列结论错误的是( ).
A.频率为 B.周期为 C.振幅为2 D.初相为
10.函数,则的最大值为( ).
A. B. C.1 D.
11.函数,若恰有3个零点,则a的取值范围是( ).
A. B. C. D.
12.已知正实数x,y,z,满足,则( ).
A. B. C. D.
第二部分(非选择题 90分)
二、填空题:本大题共4小题,每小题5分,共20分.
13.巳知冪函数的图象过点,则______.
14.角的终边经过点,则的值为______.
15.已知函数,将函数图象上各点的横坐标缩短到原来的倍(纵坐标不变),再将得到的图象向右平移个单位,得到函数的解析式______.
16.已知函数满足,当时,,若不等式的解集是集合的子集,则a的取值范围是______.
三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或推演步骤.
17.(本小题10分)计算求值:
(1)
(2)
18.(本小题12分)
已知.
(1)求的值;
(2)求的值.
19.(本小题12分)
对于函数.
(1)判断的单调性,并用定义法证明;
(2)是否存在实数a使函数为奇函数?若存在,求出a的值;若不存在,说明理由.
20.(本小题12分)
已知函数,该函数图象一条对称轴与其相邻的一个对称中心的距离为.
(1)求函数的对称轴和对称中心;
(2)求在上的单调递增区间.
21.(本小题12分)
为推动治理交通拥堵、停车难等城市病,不断提升城市道路交通治理能力现代化水平,乐山市政府决定从2021年6月1日起实施“差别化停车收费”,收费标准讨论稿如下:
A方案:首小时内3元,2-4小时为每小时1元(不足1小时按1小时计),以后每半小时1元(不足半小时按半小时计);单日最高收费不超过18元.
B方案:每小时1.6元
(1)分别求两个方案中,停车费y(元)与停车时间(小时)之间的函数关系式;
(2)假如你的停车时间不超过4小时,方案A与方案B如何选择?并说明理由.
(定义:大于或等于实数x的最小整数称为x的向上取整部分,记作,比如:,)
22.(本小题12分)
已知函数,其中.
(1)若的最小值为1,求a的值;
(2)若存在,使成立,求a的取值范围;
(3)已知,在(1)的条件下,若恒成立,求m的取值范围.
乐山市2021-2022学年高一上学期期末考试
数学参考答案及评分意见
2022.1
一、选择题:本大题共12小题,每小题5分,共60分.
1.D 【解析】由题可知,故选D.
2.A 【解析】,故选A.
3.C
【解析】由题可知,①错;,②错;,③对,故选C.
4.B
【解析】原式
,故选B.
5.B 【解析】由题可知,故选B.
6.C
【解析】因为且,则,
所以,故选C.
7.D
【解析】计算可知,每月人数增长分别为62,39,37,26,增长速度在逐月减缓,符合对数函数的特点,
故选D.
8.C
【解析】显然和为奇函数,
则和为奇函数,排除A,B,
又定义域为,排除D.故选C.
9.A
【解析】由图可知,C正确;
,则,B正确;,A错误;
因为,则,即,
又,则,D正确.故选A.
10.C
【解析】,
令,则,
当时,,故选C.
11.B 【解析】由图可知,解得,故选B.
12.A
【解析】令,
则,,,由图可知,故A.
二、填空题:本大题共4小题,每小题5分,共20分.
13.2
【解析】设,则,解得,
所以.
14.
【解析】因为,则,,
所以.
15.
【解析】将函数图象上各点的横坐标缩短到原来的倍,得,
再将得到的图象向右平移个单位得.
16.
【解析】由可知,关于对称,
又,结合函数单调性可得,
不等式等价于,即,
因为不等式解集是集合的子集,
所以,解得.
三、解答题:本大题共6小题,共70分.
17.(本小题满分10分)
【解析】(1)原式.
(2)原式.
18.(本小题满分12分)
【解析】(1)由题可知,
解得,即.
(2)原式
.
19.(本小题满分12分)
【解析】(1)在R上单调递增
证明:任取,且,
则
因为,则且且,
则,即.
所以,在R上单调递增.
(2)因为为R上的奇函数,则,所以.
20.(本小题满分12分)
【解析】(1)由题可知,
由对称轴与其相邻的一个对称中心的距离为,
得,解得,所以.
令,即,所以的对称轴为,;
令,即,所以的对称中心为,.
(2)令∵,∴,
由图可知,只需满足或,即或,
∴在上的单调递增区间是和.
21.(本小题满分12分)
【解析】(1)A方案:(未用新定义函数结果正确也给分)
B方案:.
(2)显然当时,;
又因为,,
所以存在,使得,
即,解得』
故当停车时间不超过3.75小时,选B方案;当停车时间大于3.75小时不超过4小时,选A方案.
22.(本小题满分12分)
【解析】(1)令,则,,
当时,,解得.
(2)问题等价于,
由(1)可知,,
当时,,解得.(3)问题等价于恒成立,
即,当且仅当时等号成立.
数学
第一部分(选择题 共60分)
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合,,则( ).
A. B. C. D.
2.( ).
A. B. C. D.
3.巳知集合,,有以下结论:①;②;③.其中错误的是( ).
A.①③ B.②③ C.①② D.①②③
4.( ).
A. B. C. D.1
5.已知为奇函数,当时,,则( ).
A.3 B. C.1 D.
6.巳知,,则( ).
A. B. C. D.
7.当前,全球疫情仍处于大流行状态,多国放松管控给我国外防输入带来挑战,冬季季节因素导致周边国家疫情输入我国风险大大增加.现有一组境外输人病例数据:
x(月份) 1 2 3 4 5
y(人数) 97 159 198 235 261
则x,y的函数关系与下列哪类函数最接近( ).
A. B.
C. D.
8.已知函数,,如图所示,则图象对应的解析式可能是( ).
A. B.
C. D.
9.函数的部分图象如图所示,则下列结论错误的是( ).
A.频率为 B.周期为 C.振幅为2 D.初相为
10.函数,则的最大值为( ).
A. B. C.1 D.
11.函数,若恰有3个零点,则a的取值范围是( ).
A. B. C. D.
12.已知正实数x,y,z,满足,则( ).
A. B. C. D.
第二部分(非选择题 90分)
二、填空题:本大题共4小题,每小题5分,共20分.
13.巳知冪函数的图象过点,则______.
14.角的终边经过点,则的值为______.
15.已知函数,将函数图象上各点的横坐标缩短到原来的倍(纵坐标不变),再将得到的图象向右平移个单位,得到函数的解析式______.
16.已知函数满足,当时,,若不等式的解集是集合的子集,则a的取值范围是______.
三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或推演步骤.
17.(本小题10分)计算求值:
(1)
(2)
18.(本小题12分)
已知.
(1)求的值;
(2)求的值.
19.(本小题12分)
对于函数.
(1)判断的单调性,并用定义法证明;
(2)是否存在实数a使函数为奇函数?若存在,求出a的值;若不存在,说明理由.
20.(本小题12分)
已知函数,该函数图象一条对称轴与其相邻的一个对称中心的距离为.
(1)求函数的对称轴和对称中心;
(2)求在上的单调递增区间.
21.(本小题12分)
为推动治理交通拥堵、停车难等城市病,不断提升城市道路交通治理能力现代化水平,乐山市政府决定从2021年6月1日起实施“差别化停车收费”,收费标准讨论稿如下:
A方案:首小时内3元,2-4小时为每小时1元(不足1小时按1小时计),以后每半小时1元(不足半小时按半小时计);单日最高收费不超过18元.
B方案:每小时1.6元
(1)分别求两个方案中,停车费y(元)与停车时间(小时)之间的函数关系式;
(2)假如你的停车时间不超过4小时,方案A与方案B如何选择?并说明理由.
(定义:大于或等于实数x的最小整数称为x的向上取整部分,记作,比如:,)
22.(本小题12分)
已知函数,其中.
(1)若的最小值为1,求a的值;
(2)若存在,使成立,求a的取值范围;
(3)已知,在(1)的条件下,若恒成立,求m的取值范围.
乐山市2021-2022学年高一上学期期末考试
数学参考答案及评分意见
2022.1
一、选择题:本大题共12小题,每小题5分,共60分.
1.D 【解析】由题可知,故选D.
2.A 【解析】,故选A.
3.C
【解析】由题可知,①错;,②错;,③对,故选C.
4.B
【解析】原式
,故选B.
5.B 【解析】由题可知,故选B.
6.C
【解析】因为且,则,
所以,故选C.
7.D
【解析】计算可知,每月人数增长分别为62,39,37,26,增长速度在逐月减缓,符合对数函数的特点,
故选D.
8.C
【解析】显然和为奇函数,
则和为奇函数,排除A,B,
又定义域为,排除D.故选C.
9.A
【解析】由图可知,C正确;
,则,B正确;,A错误;
因为,则,即,
又,则,D正确.故选A.
10.C
【解析】,
令,则,
当时,,故选C.
11.B 【解析】由图可知,解得,故选B.
12.A
【解析】令,
则,,,由图可知,故A.
二、填空题:本大题共4小题,每小题5分,共20分.
13.2
【解析】设,则,解得,
所以.
14.
【解析】因为,则,,
所以.
15.
【解析】将函数图象上各点的横坐标缩短到原来的倍,得,
再将得到的图象向右平移个单位得.
16.
【解析】由可知,关于对称,
又,结合函数单调性可得,
不等式等价于,即,
因为不等式解集是集合的子集,
所以,解得.
三、解答题:本大题共6小题,共70分.
17.(本小题满分10分)
【解析】(1)原式.
(2)原式.
18.(本小题满分12分)
【解析】(1)由题可知,
解得,即.
(2)原式
.
19.(本小题满分12分)
【解析】(1)在R上单调递增
证明:任取,且,
则
因为,则且且,
则,即.
所以,在R上单调递增.
(2)因为为R上的奇函数,则,所以.
20.(本小题满分12分)
【解析】(1)由题可知,
由对称轴与其相邻的一个对称中心的距离为,
得,解得,所以.
令,即,所以的对称轴为,;
令,即,所以的对称中心为,.
(2)令∵,∴,
由图可知,只需满足或,即或,
∴在上的单调递增区间是和.
21.(本小题满分12分)
【解析】(1)A方案:(未用新定义函数结果正确也给分)
B方案:.
(2)显然当时,;
又因为,,
所以存在,使得,
即,解得』
故当停车时间不超过3.75小时,选B方案;当停车时间大于3.75小时不超过4小时,选A方案.
22.(本小题满分12分)
【解析】(1)令,则,,
当时,,解得.
(2)问题等价于,
由(1)可知,,
当时,,解得.(3)问题等价于恒成立,
即,当且仅当时等号成立.
同课章节目录
