云南省丽江市古城区第一高级中学2021-2022学年高一上学期期中考试数学试题(Word版含答案)
文档属性
| 名称 | 云南省丽江市古城区第一高级中学2021-2022学年高一上学期期中考试数学试题(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 451.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-18 12:33:02 | ||
图片预览


文档简介
丽江市古城区第一高级中学2021-2022学年高一上学期期中考试
数学试卷
命题人:
本试卷分第I卷(选择题)和第II卷(非选择题)两部分.考试结束后,请讲本试卷和答题卡一并交回.满分150分,考试时间120分钟.
第I卷(选择题,共60分)
注意事项:
1.答题前,考生务必用黑色碳素笔将自己的姓名、准考证号、考场号、座位号在答题卡上填写清楚.
2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.在试卷上作答无效.
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.若,,,则=( )
A .{1,2,3} B. {2} C. {1,3,4} D. {4}
2.函数的定义域为( )
A.(,1] B.[,1] C.(,1) D.[,1)
3.下列函数中既是奇函数,又在上是增函数的为( )
A. B. C. D.
4.下列四组函数,表示同一函数的是 ( )
A. B.
C. D. ,
5.已知函数的图像恒过定点P,则P点坐标是( )
A. (1,5) B. (1,4) C. (0,4) D. (4,0)
6.函数 ,若,则的值是( )
A.或-1 B. C.戓-1 D.-1
7.函数的零点所在的大致区间是( )
A. B. C. D.
8.设,,,则的大小关系为( )
A. B. C. D.
9.若函数是定义在R上的偶函数,在上是减函数,且,则使得的的取值范围是( )
A. B. C. D.
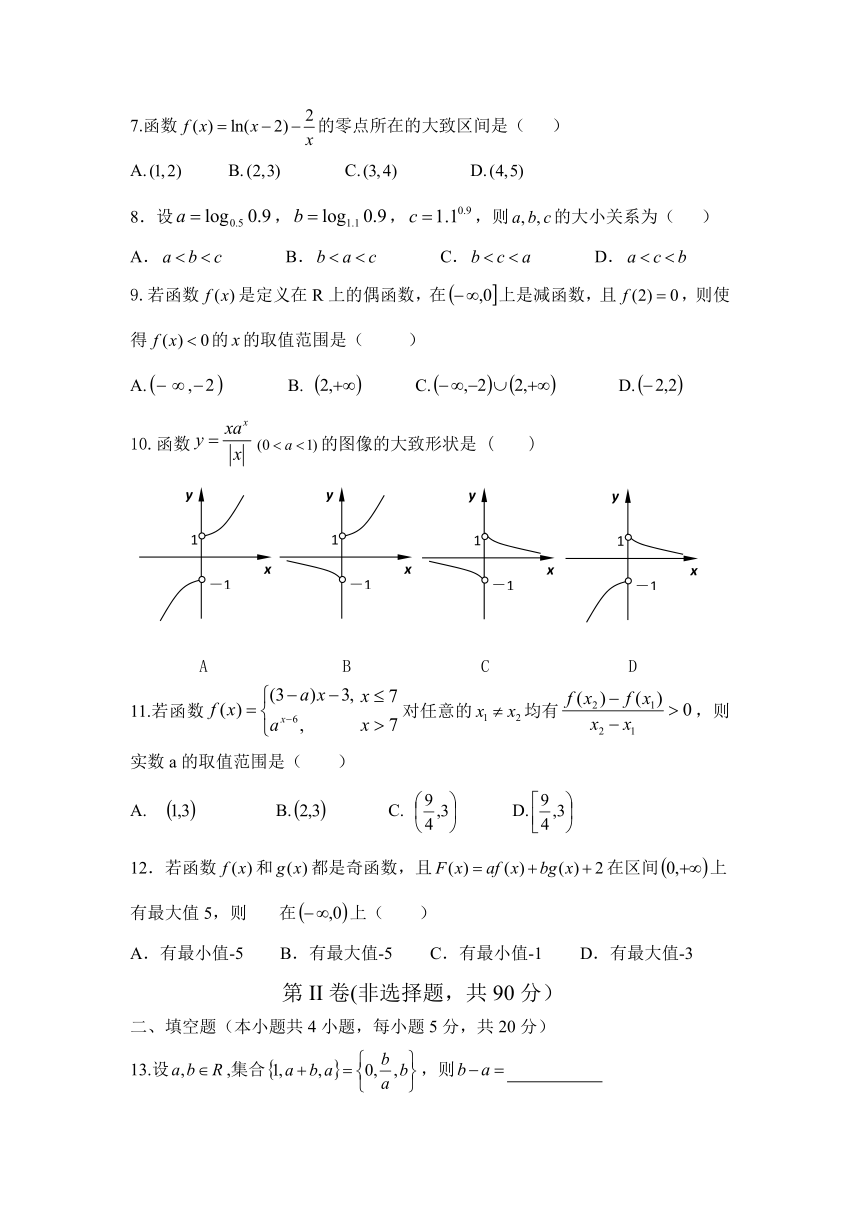
10.函数的图像的大致形状是 ( )
A B C D
11.若函数对任意的均有,则实数a的取值范围是( )
A. B. C. D.
12.若函数和都是奇函数,且在区间上有最大值5,则在上( )
A.有最小值-5 B.有最大值-5 C.有最小值-1 D.有最大值-3
第II卷(非选择题,共90分)
2、填空题(本小题共4小题,每小题5分,共20分)
13.设,集合,则
14.已知是定义在上的奇函数,当时,,则时,__________.
15.已知函数在区间上是减函数,则的取值范围是
.
16.已知函数,若函数的图象有两个不同交点,则实数取值范围是_______.
3、解答题(共70分,解答应写出必要文字说明,证明过程或演算步骤)
17.(本小题满分10分)
计算下列各式的值:
18.(本小题满分12分)
(1)设集合,.若A∪B=B,求实数的取值范围.
(2)已知,求实数的取值范围.
19.(本小题满分12分)
设函数=,.
(I)利用单调性定义证明:在区间上是单调递减函数;
(II)当时,求在区间上的最大值。
20、(本小题满分12分)
共享单车是城市慢行系统的一种模式创新,对于解决民众出行“最后一公里”的问题特别见效,由于停取方便、租用价格低廉,各色共享单车受到人们的热捧.某自行车厂为共享单车公司生产新样式的单车,已知生产新样式单车的固定成本为20000元,每生产一件新样式单车需要增加投入100元.根据初步测算,自行车厂的总收益(单位:元)满足分段函数,
其中 是新样式单车的月产量(单位:件),利润总收益总成本.
(1)试将自行车厂的利润元表示为月产量的函数;
(2)当月产量为多少件时自行车厂的利润最大?最大利润是多少?
21.(本小题满分12分)
已知函数在区间上的值域为.
(1)求的值;
(2)函数,不等式在上恒成立,求实数的取值范围.
22.(本小题满分12分)
已知定义在R上的函数是奇函数.
(1)求的值;
(2)判断的单调性,并证明你的判断;
(3)若对任意的,不等式恒成立,求实数的取值范围.
答案
1 2 3 4 5 6 7 8 9 10 11 12
C A B B A C C B D D D C
13.设,集合,则2
解:根据题意,集合,又∵a≠0,∴a+b=0,即a=-b,
∴,b=1;故a=-1,b=1,则b-a=2,
14【答案】
15 .
16___
17
18解:(1) ∵若A∪B=B,∴A B 则a+1≤-1或a-1≥2,
解得:a≤-2或a≥3,则实数a的取值范围为(-∞,-2]∪[3,+∞).
(2)可化为
当时,不等式恒成立;
当时,,
综上所述:实数a的取值范围是:。
19解:(I)任取,∈(0,2],设<,则
∵,∴
∵,∴<4
∴
所以,故在区间(0,2]上是单调递减函数。 6分
(II)由(I)可知,在区间(0,2]上是单调递减函数;
当,设<,易知总有<,
所以在区间[2,+∞)上是单调递增函数。
又,所以在区间上最大值为。 12分
20(1)依题设,总成本为,
则
(2)当时, ,
则当时, ;
当时, 是减函数,
则,
所以,当月产量件时,自行车厂的利润最大,最大利润为25000元.
21解:(1),对称轴,
因为,在上为增函数,
.
(2),
不等式可化为,
令,,记,
则,所以. 所以的取值范围是.
22解:(1)∵是定义在R上的奇函数,∴,∴ 2分
,
∴即对一切实数都成立,
∴∴ 4分
(2),在R上是减函数
证明:设且
则
∵,∴,,,∴
即,∴在R上是减函数 8分
(3)不等式
又是R上的减函数, ∴
∴对恒成立 ∴ 12分
x
y
O
1
-1
x
y
O
1
-1
x
y
O
1
-1
x
y
O
1
-1
数学试卷
命题人:
本试卷分第I卷(选择题)和第II卷(非选择题)两部分.考试结束后,请讲本试卷和答题卡一并交回.满分150分,考试时间120分钟.
第I卷(选择题,共60分)
注意事项:
1.答题前,考生务必用黑色碳素笔将自己的姓名、准考证号、考场号、座位号在答题卡上填写清楚.
2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.在试卷上作答无效.
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.若,,,则=( )
A .{1,2,3} B. {2} C. {1,3,4} D. {4}
2.函数的定义域为( )
A.(,1] B.[,1] C.(,1) D.[,1)
3.下列函数中既是奇函数,又在上是增函数的为( )
A. B. C. D.
4.下列四组函数,表示同一函数的是 ( )
A. B.
C. D. ,
5.已知函数的图像恒过定点P,则P点坐标是( )
A. (1,5) B. (1,4) C. (0,4) D. (4,0)
6.函数 ,若,则的值是( )
A.或-1 B. C.戓-1 D.-1
7.函数的零点所在的大致区间是( )
A. B. C. D.
8.设,,,则的大小关系为( )
A. B. C. D.
9.若函数是定义在R上的偶函数,在上是减函数,且,则使得的的取值范围是( )
A. B. C. D.
10.函数的图像的大致形状是 ( )
A B C D
11.若函数对任意的均有,则实数a的取值范围是( )
A. B. C. D.
12.若函数和都是奇函数,且在区间上有最大值5,则在上( )
A.有最小值-5 B.有最大值-5 C.有最小值-1 D.有最大值-3
第II卷(非选择题,共90分)
2、填空题(本小题共4小题,每小题5分,共20分)
13.设,集合,则
14.已知是定义在上的奇函数,当时,,则时,__________.
15.已知函数在区间上是减函数,则的取值范围是
.
16.已知函数,若函数的图象有两个不同交点,则实数取值范围是_______.
3、解答题(共70分,解答应写出必要文字说明,证明过程或演算步骤)
17.(本小题满分10分)
计算下列各式的值:
18.(本小题满分12分)
(1)设集合,.若A∪B=B,求实数的取值范围.
(2)已知,求实数的取值范围.
19.(本小题满分12分)
设函数=,.
(I)利用单调性定义证明:在区间上是单调递减函数;
(II)当时,求在区间上的最大值。
20、(本小题满分12分)
共享单车是城市慢行系统的一种模式创新,对于解决民众出行“最后一公里”的问题特别见效,由于停取方便、租用价格低廉,各色共享单车受到人们的热捧.某自行车厂为共享单车公司生产新样式的单车,已知生产新样式单车的固定成本为20000元,每生产一件新样式单车需要增加投入100元.根据初步测算,自行车厂的总收益(单位:元)满足分段函数,
其中 是新样式单车的月产量(单位:件),利润总收益总成本.
(1)试将自行车厂的利润元表示为月产量的函数;
(2)当月产量为多少件时自行车厂的利润最大?最大利润是多少?
21.(本小题满分12分)
已知函数在区间上的值域为.
(1)求的值;
(2)函数,不等式在上恒成立,求实数的取值范围.
22.(本小题满分12分)
已知定义在R上的函数是奇函数.
(1)求的值;
(2)判断的单调性,并证明你的判断;
(3)若对任意的,不等式恒成立,求实数的取值范围.
答案
1 2 3 4 5 6 7 8 9 10 11 12
C A B B A C C B D D D C
13.设,集合,则2
解:根据题意,集合,又∵a≠0,∴a+b=0,即a=-b,
∴,b=1;故a=-1,b=1,则b-a=2,
14【答案】
15 .
16___
17
18解:(1) ∵若A∪B=B,∴A B 则a+1≤-1或a-1≥2,
解得:a≤-2或a≥3,则实数a的取值范围为(-∞,-2]∪[3,+∞).
(2)可化为
当时,不等式恒成立;
当时,,
综上所述:实数a的取值范围是:。
19解:(I)任取,∈(0,2],设<,则
∵,∴
∵,∴<4
∴
所以,故在区间(0,2]上是单调递减函数。 6分
(II)由(I)可知,在区间(0,2]上是单调递减函数;
当,设<,易知总有<,
所以在区间[2,+∞)上是单调递增函数。
又,所以在区间上最大值为。 12分
20(1)依题设,总成本为,
则
(2)当时, ,
则当时, ;
当时, 是减函数,
则,
所以,当月产量件时,自行车厂的利润最大,最大利润为25000元.
21解:(1),对称轴,
因为,在上为增函数,
.
(2),
不等式可化为,
令,,记,
则,所以. 所以的取值范围是.
22解:(1)∵是定义在R上的奇函数,∴,∴ 2分
,
∴即对一切实数都成立,
∴∴ 4分
(2),在R上是减函数
证明:设且
则
∵,∴,,,∴
即,∴在R上是减函数 8分
(3)不等式
又是R上的减函数, ∴
∴对恒成立 ∴ 12分
x
y
O
1
-1
x
y
O
1
-1
x
y
O
1
-1
x
y
O
1
-1
同课章节目录
