华东师大版数学九年级上册 25.2.1 概率及其意义教案(表格式)
文档属性
| 名称 | 华东师大版数学九年级上册 25.2.1 概率及其意义教案(表格式) |
|
|
| 格式 | docx | ||
| 文件大小 | 58.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-18 10:49:44 | ||
图片预览


文档简介
概率及其意义
教学目标 1.理解概率的含义及概率的取值范围; 2.用实验的方法分析随机事件的概率; 3.会用数学语言表示概率。
教学 重难点 1.重点:会分析实验结果,会用概率表示实验结果。
2.难点:概率值的正确含义。
教学方法 实验、自主探索。
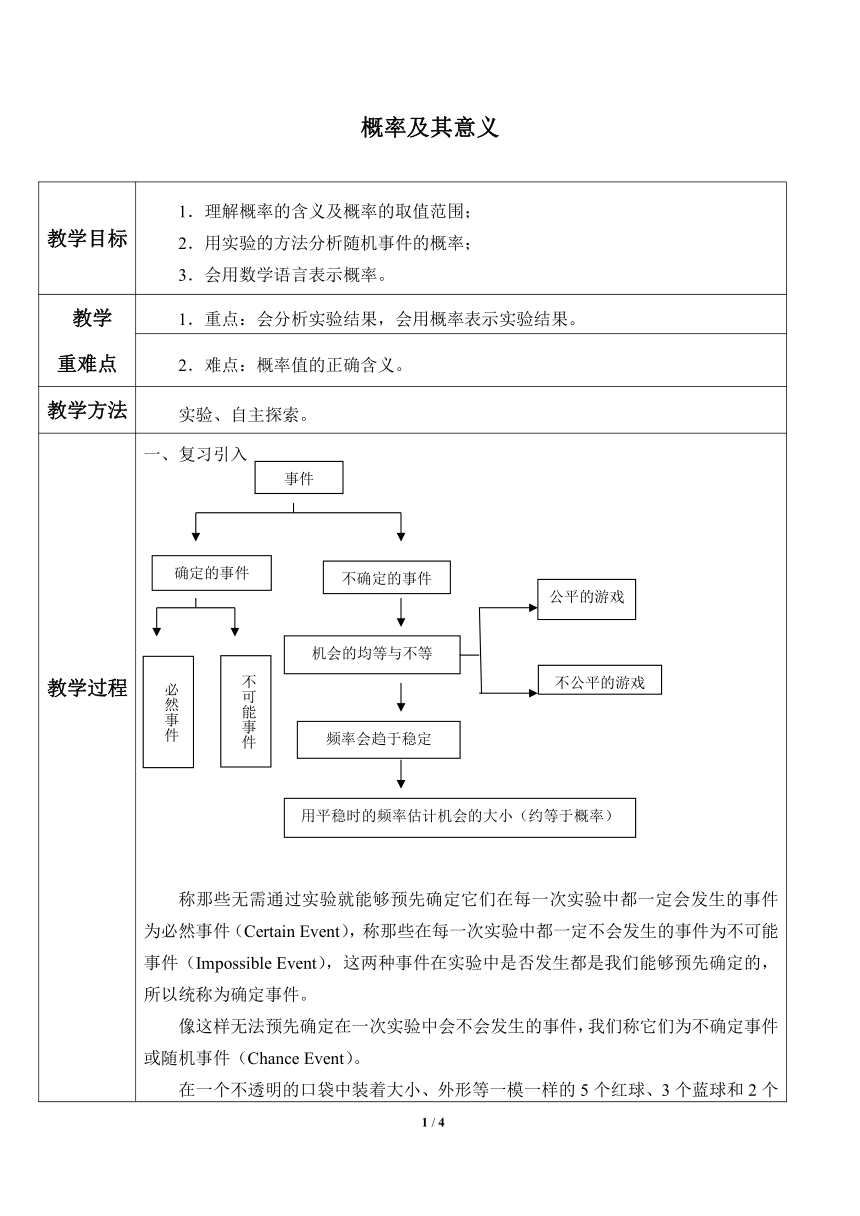
教学过程 一、复习引入 称那些无需通过实验就能够预先确定它们在每一次实验中都一定会发生的事件为必然事件(Certain Event),称那些在每一次实验中都一定不会发生的事件为不可能事件(Impossible Event),这两种事件在实验中是否发生都是我们能够预先确定的,所以统称为确定事件。 像这样无法预先确定在一次实验中会不会发生的事件,我们称它们为不确定事件或随机事件(Chance Event)。 在一个不透明的口袋中装着大小、外形等一模一样的5个红球、3个蓝球和2个白球,它们已经在口袋中被搅匀了。请判断下面哪些是不可能事件,哪些是必然事件,哪些是随机事件,并说明理由。 从口袋中任意取出1个球,是一个白球; 从口袋中一次任意取出5个球,全是蓝球; 从口袋中一次任意取出5个球,只是蓝球和白球,没有红球; 从口袋中一次任意取出6个球,恰好红、蓝、白三种颜色的球都齐了; 从口袋中一次任意取出9个球,恰好红、蓝、白三种颜色的球都齐了; 分析:有底纹字句的作用是什么?(说明机会均等) 答案:(随机事件)、(不可能事件)、(随机事件)、(随机事件)、(必然事件)。 二、新课讲解 1.给5分钟学生默读课文。然后提问以下三个问题,让学生尝试找出答案。 (1)概率的概念:表示一个事件发生的可能性大小的这个数,叫做该事件的概率(probability)。 (2)概率的表示方法:P(关注的结果)=数(这个数在0与1之间)。 (3)求概率值的方法:A.通过重复实验、观察频率的稳定值;B.通过分析可能发生的结果,计算出来:关注的结果发生的个数÷所有机会均等的结果发生的个数。 做过的几个实验及其实验结果: 实验关注的结果频率稳定值所有机会均等的结果。关注结果发生的概率。抛掷一枚硬币。正面0.5左右正面;反面。抛掷两枚硬币。两个正面0.25左右两个正面;两个反面;先正后反;先反后正。投掷一枚四面体骰子。掷得“4”0.25左右数字:“1”;“2”;“3”;“4”。投掷一枚六面体骰子。掷得“6”0.167左右从一副没有大小王的扑克牌中随机地抽一张。黑桃0.25左右
指导学生分析“所有机会均等的结果”,完成表的第四列填空。 指导学生计算概率,完成表的第五列填空,并对比第三列的对应值。 重点分析第三行:关注的结果个数为1,所有机会均等的结果个数为4,而不要错误理解“两个正面”为结果个数是2,错误理解“两个正面;两个反面;先正后反;先反后正”为结果个数是6。“一正一反”的说法包括“先正后反”和“先反后正”两个结果。 重点分析第四行:关注的结果个数为1,所有机会均等的结果个数为4,而不要错误理解“掷得‘4’”为结果个数是4,“4”是一个事件而不是结果的个数。 P(掷得“6”)=,读作:掷得“6”的概率等于。 2.概率值的解释。 掷得“6”的概率等于表示什么意思?让学生充分讨论。 学生讨论后,把学生的主要意见板书于黑板,然后让学生做投掷骰子实验,一旦掷到“6”,就算完成了1次实验。每位学生做一次,然后把结果记录下来,模仿表做好实验记录。(实验在课前完成) 把全班学生的实验结果汇总到一张表上,然后计算实验的平均值,看看平均几次才有1次掷得“6”? 对比实验结果,公布概率的正确含义,并分析学生先前的意见。 掷得“6”的概率等于表示:如果掷很多很多次的话,那么平均每6次有1次掷出“6”。注意前提是:掷很多很多次,也就是说,实验的次数要足够多,要重复实验取稳定频率。在回答这类问题时,必须加上这句话,否则表达就不够准确。 3.思考。 已知掷得“6”的概率等于,那么不是“6”(也就是1~5)的概率等于多少呢?这个概率值又表示什么意思? 我们知道,掷得“6”的概率等于也表示:如果重复投掷骰子很多很多次的话,那么实验中掷得“6”的频率会逐渐稳定到附近。这与“平均每6次有1次掷出‘6’”互相矛盾吗? 答案:(1)P(不是“6”)=,这个概率值表示:如果掷很多很多次的话,那么平均每6次有5次掷得不是“6”。 (2)不矛盾,这两种说法是一回事。 4.巩固练习 你同意以下说法吗?请说明理由。 (1)“从布袋中取出一只红球的概率是99%”,这句话的意思就是:肯定会取出一只红球,因为概率已经很大了; (2)“从布袋中取出一只红球的概率是0”,这句话的意思就是:取出一只红球的可能性很小; (3)布袋中有红、白、黑三种颜色的球,这些球除颜色外没有任何其他区别。因为我对取出一只红球没有把握,所以我就说“从布袋中取出一只红球的概率是50%”; (4)“从布袋中取出一只红球的概率是0.1%”,这句话的意思就是说话的人认为一定取不到红球; 练习:投掷一个均匀的正八面体骰子,每个面上依次标有1、2、3、4、5、6、7和8。 (1)掷得“7”的概率等于多少?这个数表示什么意思? (2)掷得的数不是“7”的概率等于多少?这个数表示什么意思? (3)掷得的数小于或等于“6”的概率等于多少?这个数表示什么意思? 三、小结 事件分为确定事件与不确定事件(随机事件),概率一般研究随机事件。确定事件的概率已经很明确,P(必然事件)=1,P(不可能事件)=0,0 < P(随机事件)< 1。 会分析关注的结果以及所有机会均等的结果; 会表达概率值的含义。
4 / 4
教学目标 1.理解概率的含义及概率的取值范围; 2.用实验的方法分析随机事件的概率; 3.会用数学语言表示概率。
教学 重难点 1.重点:会分析实验结果,会用概率表示实验结果。
2.难点:概率值的正确含义。
教学方法 实验、自主探索。
教学过程 一、复习引入 称那些无需通过实验就能够预先确定它们在每一次实验中都一定会发生的事件为必然事件(Certain Event),称那些在每一次实验中都一定不会发生的事件为不可能事件(Impossible Event),这两种事件在实验中是否发生都是我们能够预先确定的,所以统称为确定事件。 像这样无法预先确定在一次实验中会不会发生的事件,我们称它们为不确定事件或随机事件(Chance Event)。 在一个不透明的口袋中装着大小、外形等一模一样的5个红球、3个蓝球和2个白球,它们已经在口袋中被搅匀了。请判断下面哪些是不可能事件,哪些是必然事件,哪些是随机事件,并说明理由。 从口袋中任意取出1个球,是一个白球; 从口袋中一次任意取出5个球,全是蓝球; 从口袋中一次任意取出5个球,只是蓝球和白球,没有红球; 从口袋中一次任意取出6个球,恰好红、蓝、白三种颜色的球都齐了; 从口袋中一次任意取出9个球,恰好红、蓝、白三种颜色的球都齐了; 分析:有底纹字句的作用是什么?(说明机会均等) 答案:(随机事件)、(不可能事件)、(随机事件)、(随机事件)、(必然事件)。 二、新课讲解 1.给5分钟学生默读课文。然后提问以下三个问题,让学生尝试找出答案。 (1)概率的概念:表示一个事件发生的可能性大小的这个数,叫做该事件的概率(probability)。 (2)概率的表示方法:P(关注的结果)=数(这个数在0与1之间)。 (3)求概率值的方法:A.通过重复实验、观察频率的稳定值;B.通过分析可能发生的结果,计算出来:关注的结果发生的个数÷所有机会均等的结果发生的个数。 做过的几个实验及其实验结果: 实验关注的结果频率稳定值所有机会均等的结果。关注结果发生的概率。抛掷一枚硬币。正面0.5左右正面;反面。抛掷两枚硬币。两个正面0.25左右两个正面;两个反面;先正后反;先反后正。投掷一枚四面体骰子。掷得“4”0.25左右数字:“1”;“2”;“3”;“4”。投掷一枚六面体骰子。掷得“6”0.167左右从一副没有大小王的扑克牌中随机地抽一张。黑桃0.25左右
指导学生分析“所有机会均等的结果”,完成表的第四列填空。 指导学生计算概率,完成表的第五列填空,并对比第三列的对应值。 重点分析第三行:关注的结果个数为1,所有机会均等的结果个数为4,而不要错误理解“两个正面”为结果个数是2,错误理解“两个正面;两个反面;先正后反;先反后正”为结果个数是6。“一正一反”的说法包括“先正后反”和“先反后正”两个结果。 重点分析第四行:关注的结果个数为1,所有机会均等的结果个数为4,而不要错误理解“掷得‘4’”为结果个数是4,“4”是一个事件而不是结果的个数。 P(掷得“6”)=,读作:掷得“6”的概率等于。 2.概率值的解释。 掷得“6”的概率等于表示什么意思?让学生充分讨论。 学生讨论后,把学生的主要意见板书于黑板,然后让学生做投掷骰子实验,一旦掷到“6”,就算完成了1次实验。每位学生做一次,然后把结果记录下来,模仿表做好实验记录。(实验在课前完成) 把全班学生的实验结果汇总到一张表上,然后计算实验的平均值,看看平均几次才有1次掷得“6”? 对比实验结果,公布概率的正确含义,并分析学生先前的意见。 掷得“6”的概率等于表示:如果掷很多很多次的话,那么平均每6次有1次掷出“6”。注意前提是:掷很多很多次,也就是说,实验的次数要足够多,要重复实验取稳定频率。在回答这类问题时,必须加上这句话,否则表达就不够准确。 3.思考。 已知掷得“6”的概率等于,那么不是“6”(也就是1~5)的概率等于多少呢?这个概率值又表示什么意思? 我们知道,掷得“6”的概率等于也表示:如果重复投掷骰子很多很多次的话,那么实验中掷得“6”的频率会逐渐稳定到附近。这与“平均每6次有1次掷出‘6’”互相矛盾吗? 答案:(1)P(不是“6”)=,这个概率值表示:如果掷很多很多次的话,那么平均每6次有5次掷得不是“6”。 (2)不矛盾,这两种说法是一回事。 4.巩固练习 你同意以下说法吗?请说明理由。 (1)“从布袋中取出一只红球的概率是99%”,这句话的意思就是:肯定会取出一只红球,因为概率已经很大了; (2)“从布袋中取出一只红球的概率是0”,这句话的意思就是:取出一只红球的可能性很小; (3)布袋中有红、白、黑三种颜色的球,这些球除颜色外没有任何其他区别。因为我对取出一只红球没有把握,所以我就说“从布袋中取出一只红球的概率是50%”; (4)“从布袋中取出一只红球的概率是0.1%”,这句话的意思就是说话的人认为一定取不到红球; 练习:投掷一个均匀的正八面体骰子,每个面上依次标有1、2、3、4、5、6、7和8。 (1)掷得“7”的概率等于多少?这个数表示什么意思? (2)掷得的数不是“7”的概率等于多少?这个数表示什么意思? (3)掷得的数小于或等于“6”的概率等于多少?这个数表示什么意思? 三、小结 事件分为确定事件与不确定事件(随机事件),概率一般研究随机事件。确定事件的概率已经很明确,P(必然事件)=1,P(不可能事件)=0,0 < P(随机事件)< 1。 会分析关注的结果以及所有机会均等的结果; 会表达概率值的含义。
4 / 4
