人教版数学八年级下册 16.2 二次根式的乘除法课件(共42张PPT)
文档属性
| 名称 | 人教版数学八年级下册 16.2 二次根式的乘除法课件(共42张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-18 11:28:26 | ||
图片预览







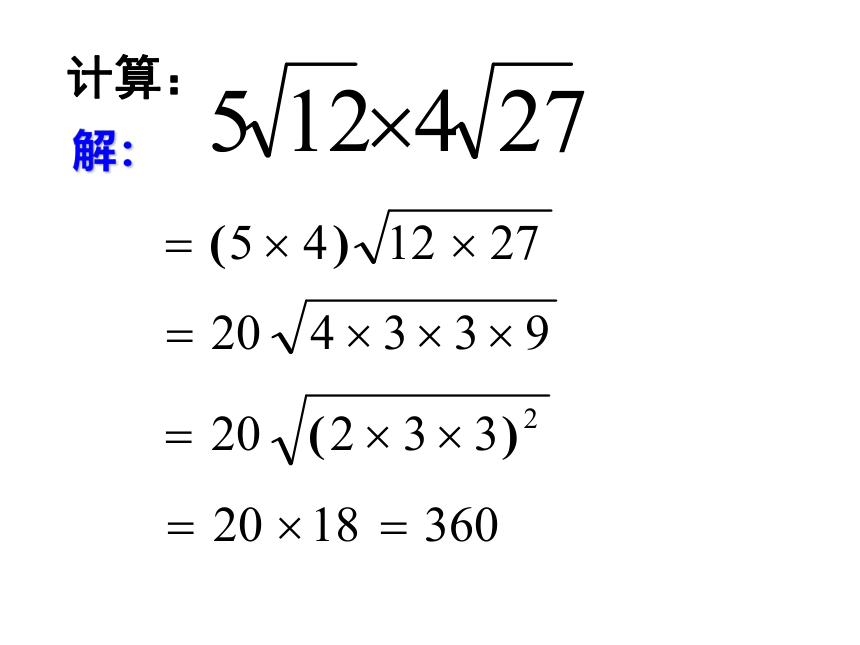



文档简介
(共42张PPT)
复习归纳
二次根式的性质:
(a≥0)
(1)
(2)
a
-a
当a≥0时,= ;
当a≤0时,= .
|a|
a
复习归纳
二次根式的性质:
(3)
(4)
(a ≥0 , b>0)
(a ≥0 , b≥0)
回顾:
你会计算吗 (1) (2)
有简便的方法吗 根据什么
积和商的二次根式的性质:
反过来:
二次根式乘除运算法则
二次根式相乘:被开方数相乘, 根指数不变;
化简。
(默1))
你能用上面二次根式乘法法则来计算吗?
例1 计算:
解:原式
原式
二次根式乘除运算的一般步骤:
1.运用法则,化归为根号内的实数运算;
2.完成根号内相乘,相除(约分)等运算;
3.化简二次根式.
(默2)
例1 计算:
解:原式
原式
根号外的系数与系数相乘,积为结果的系数。
分子约分后,分解素因数,找平方的项开出,不必马上乘出来
解:
计算:
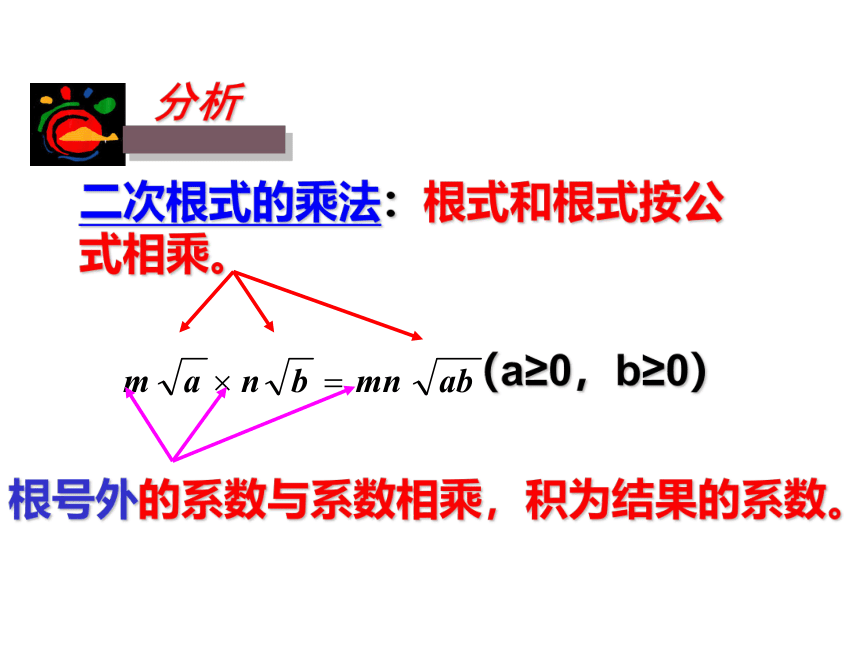
(a≥0,b≥0)
根号外的系数与系数相乘,积为结果的系数。
二次根式的乘法:根式和根式按公式相乘。
分析
计算:
结果必须化为最简二次根式.
找因数的最大公因数,不行再分解因数
(默3)
要先相乘,后化简。
计算:
分子约分后,分解素因数,找平方的项开出,不必马上乘出来
二次根式乘除运算的一般步骤:
1.运用法则,化归为根号内的实数运算;
2.完成根号内相乘,相除(约分)等运算;
3.化简二次根式.
(a≥0,b≥0)
根号外的系数与系数相乘,积为结果的系数。
二次根式的乘法:根式和根式按公式相乘。
例2:计算
解:
两个二次根式相除,等于把被开方数相除,作为商的被开方数
试一试
计算:
解:
如果根号前有系数,就把系数相除,仍旧作为二次根号前的系数。
例题2 计算
(2)
(u>0)
(a>b>0)
分子和分母乘除后,分别分解素因数,找平方的项开出,不必马上乘出来(分母必须是平方的项)
多项式先因式分解,再乘除
(默4)
二次根式乘除运算的一般步骤:
1.运用法则,化归为根号内的实数运算;
2.完成根号内相乘,相除(约分)等运算;
3.化简二次根式.
分子和分母乘除后,分别分解素因数,找平方的项开出,不必马上乘出来(分母必须是平方的项)
多项式先因式分解,再乘除
二次根式的乘除法:
根式和根式按公式相乘除。
根号外的系数与系数相乘除,积为结果的系数
(默2)
例3 计算:
(2)
(1)
解:原式
解:原式
计算:
二次根式的连乘除运算,从左向右依次计算或系数相乘除作为系数;根式相乘除。
(默5)
计算
解;原式=
计算
原式=
计算:(1)
(2)
(2)原式=
(1)原式=
解:
原式
二次根式的运算(乘除运算):
归纳小结
(a ≥0 , b≥0)
(a ≥0 , b>0)
二次根式乘除运算的一般步骤:
1.运用法则,化归为根号内的实数运算;
2.完成根号内相乘,相除(约分)等运算;
3.化简二次根式.
分子和分母乘除后,分别分解素因数,找平方的项开出,不必马上乘出来(分母必须是平方的项)
多项式先因式分解,再乘除
二次根式的乘除法:
根式和根式按公式相乘除。
根号外的系数与系数相乘除,积为结果的系数
二次根式的连乘除运算,从左向右依次计算或系数相乘除作为系数;根式相乘除。
(默2)
1.计算:
;
6
24
)
4
(
.
)
6
(
3
x
ax
;
5
45
)
5
(
;
14
7
)
1
(
·
;
6
2
)
2
(
xy
x
·
;
)
3
(
3
b
a
a
b
·
a
2
3
2
7
y
x
3
2
a
x
解:
计算:
);
27
5
(
15
)
1
(
·
;
3
1
=
9
1
=
27
5
15
×
=
27
5
15
×
=
)
27
5
(
15
)
1
(
·
解:
2.计算:
;
3
2
6
)
1
(
·
3
.
5
3
24
15
)
2
(
·
4
6
计算(字母为正数)
典型例题
计算
点评:也可以用“除以一个数,等于乘以这个数的倒数”的法则进行计算.
2.填空
选做题 (A组)
- 4 13
8.64
-3- 10
√
选做题 (B组)
√
√
√
达标反馈
1.判断:(对的打√,错的打×)
( )
2.填空:
×
例题赏识:
1.计算(1)
(2)
(3)
2.已知
,求
的值。
3.已知
、
,求
的值。
4.已知x满足
y是
的整数部分,求
巩固提升:
5.
=_____
6.
=__________
7.
=________
8.已知a为实数,则代数式 = _____
0
4
12
9.已知
是正整数,则实数n的最大值是________
10.化简:
= __________
=________
11.化简:
11
反过来就是
把下列各式中根号外的正因式移进根号内
(1)
(2)
(3)
(4)
根号外的负因式不能移进根号内,在移进根号内之前一定要先判断是否为非负因式.
练习二:
-21
C
复习归纳
二次根式的性质:
(a≥0)
(1)
(2)
a
-a
当a≥0时,= ;
当a≤0时,= .
|a|
a
复习归纳
二次根式的性质:
(3)
(4)
(a ≥0 , b>0)
(a ≥0 , b≥0)
回顾:
你会计算吗 (1) (2)
有简便的方法吗 根据什么
积和商的二次根式的性质:
反过来:
二次根式乘除运算法则
二次根式相乘:被开方数相乘, 根指数不变;
化简。
(默1))
你能用上面二次根式乘法法则来计算吗?
例1 计算:
解:原式
原式
二次根式乘除运算的一般步骤:
1.运用法则,化归为根号内的实数运算;
2.完成根号内相乘,相除(约分)等运算;
3.化简二次根式.
(默2)
例1 计算:
解:原式
原式
根号外的系数与系数相乘,积为结果的系数。
分子约分后,分解素因数,找平方的项开出,不必马上乘出来
解:
计算:
(a≥0,b≥0)
根号外的系数与系数相乘,积为结果的系数。
二次根式的乘法:根式和根式按公式相乘。
分析
计算:
结果必须化为最简二次根式.
找因数的最大公因数,不行再分解因数
(默3)
要先相乘,后化简。
计算:
分子约分后,分解素因数,找平方的项开出,不必马上乘出来
二次根式乘除运算的一般步骤:
1.运用法则,化归为根号内的实数运算;
2.完成根号内相乘,相除(约分)等运算;
3.化简二次根式.
(a≥0,b≥0)
根号外的系数与系数相乘,积为结果的系数。
二次根式的乘法:根式和根式按公式相乘。
例2:计算
解:
两个二次根式相除,等于把被开方数相除,作为商的被开方数
试一试
计算:
解:
如果根号前有系数,就把系数相除,仍旧作为二次根号前的系数。
例题2 计算
(2)
(u>0)
(a>b>0)
分子和分母乘除后,分别分解素因数,找平方的项开出,不必马上乘出来(分母必须是平方的项)
多项式先因式分解,再乘除
(默4)
二次根式乘除运算的一般步骤:
1.运用法则,化归为根号内的实数运算;
2.完成根号内相乘,相除(约分)等运算;
3.化简二次根式.
分子和分母乘除后,分别分解素因数,找平方的项开出,不必马上乘出来(分母必须是平方的项)
多项式先因式分解,再乘除
二次根式的乘除法:
根式和根式按公式相乘除。
根号外的系数与系数相乘除,积为结果的系数
(默2)
例3 计算:
(2)
(1)
解:原式
解:原式
计算:
二次根式的连乘除运算,从左向右依次计算或系数相乘除作为系数;根式相乘除。
(默5)
计算
解;原式=
计算
原式=
计算:(1)
(2)
(2)原式=
(1)原式=
解:
原式
二次根式的运算(乘除运算):
归纳小结
(a ≥0 , b≥0)
(a ≥0 , b>0)
二次根式乘除运算的一般步骤:
1.运用法则,化归为根号内的实数运算;
2.完成根号内相乘,相除(约分)等运算;
3.化简二次根式.
分子和分母乘除后,分别分解素因数,找平方的项开出,不必马上乘出来(分母必须是平方的项)
多项式先因式分解,再乘除
二次根式的乘除法:
根式和根式按公式相乘除。
根号外的系数与系数相乘除,积为结果的系数
二次根式的连乘除运算,从左向右依次计算或系数相乘除作为系数;根式相乘除。
(默2)
1.计算:
;
6
24
)
4
(
.
)
6
(
3
x
ax
;
5
45
)
5
(
;
14
7
)
1
(
·
;
6
2
)
2
(
xy
x
·
;
)
3
(
3
b
a
a
b
·
a
2
3
2
7
y
x
3
2
a
x
解:
计算:
);
27
5
(
15
)
1
(
·
;
3
1
=
9
1
=
27
5
15
×
=
27
5
15
×
=
)
27
5
(
15
)
1
(
·
解:
2.计算:
;
3
2
6
)
1
(
·
3
.
5
3
24
15
)
2
(
·
4
6
计算(字母为正数)
典型例题
计算
点评:也可以用“除以一个数,等于乘以这个数的倒数”的法则进行计算.
2.填空
选做题 (A组)
- 4 13
8.64
-3- 10
√
选做题 (B组)
√
√
√
达标反馈
1.判断:(对的打√,错的打×)
( )
2.填空:
×
例题赏识:
1.计算(1)
(2)
(3)
2.已知
,求
的值。
3.已知
、
,求
的值。
4.已知x满足
y是
的整数部分,求
巩固提升:
5.
=_____
6.
=__________
7.
=________
8.已知a为实数,则代数式 = _____
0
4
12
9.已知
是正整数,则实数n的最大值是________
10.化简:
= __________
=________
11.化简:
11
反过来就是
把下列各式中根号外的正因式移进根号内
(1)
(2)
(3)
(4)
根号外的负因式不能移进根号内,在移进根号内之前一定要先判断是否为非负因式.
练习二:
-2
C
