人教A版(2019)必修第一册必杀技第五章5.6函数word版含答案.docx
文档属性
| 名称 | 人教A版(2019)必修第一册必杀技第五章5.6函数word版含答案.docx |

|
|
| 格式 | docx | ||
| 文件大小 | 824.2KB | ||
| 资源类型 | 教案 | ||
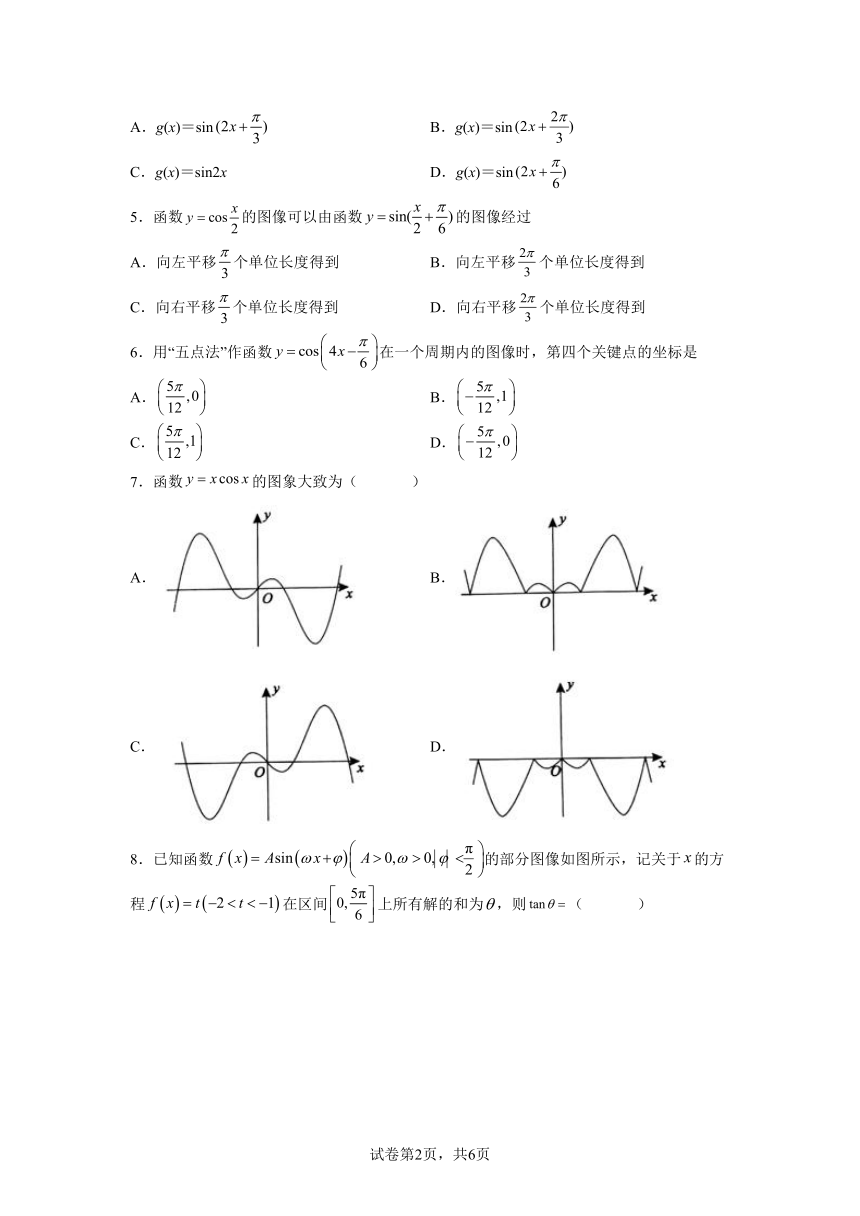
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-19 10:51:23 | ||
图片预览



文档简介
人教A版(2019)必修第一册必杀技第五章5.6函数
一、单选题
1.要得到函数的图象,只需将的图象( )
A.向左平移个单位长度 B.向右平移个单位长度
C.向左平移个单位长度 D.向右平移个单位长度
2.的振幅、频率和初相分别为
A. B.
C. D.
3.已知且为整数,且,函数的图像如图所示,A、C,D是的图像与相邻的三个交点,与x轴交于相邻的两个交点O、B,若在区间上,有2020个零点,则的最大值为( )
A. B.
C. D.
4.若将函数g(x)图象上所有的点向左平移个单位长度得到函数f(x)的图象,已知函数f(x)=Asin(ωx+φ)的部分图象如图所示,则( )
A.g(x)=sin B.g(x)=sin
C.g(x)=sin2x D.g(x)=sin
5.函数的图像可以由函数的图像经过
A.向左平移个单位长度得到 B.向左平移个单位长度得到
C.向右平移个单位长度得到 D.向右平移个单位长度得到
6.用“五点法”作函数在一个周期内的图像时,第四个关键点的坐标是
A. B.
C. D.
7.函数的图象大致为( )
A. B.
C. D.
8.已知函数的部分图像如图所示,记关于的方程在区间上所有解的和为,则( )
A. B. C. D.
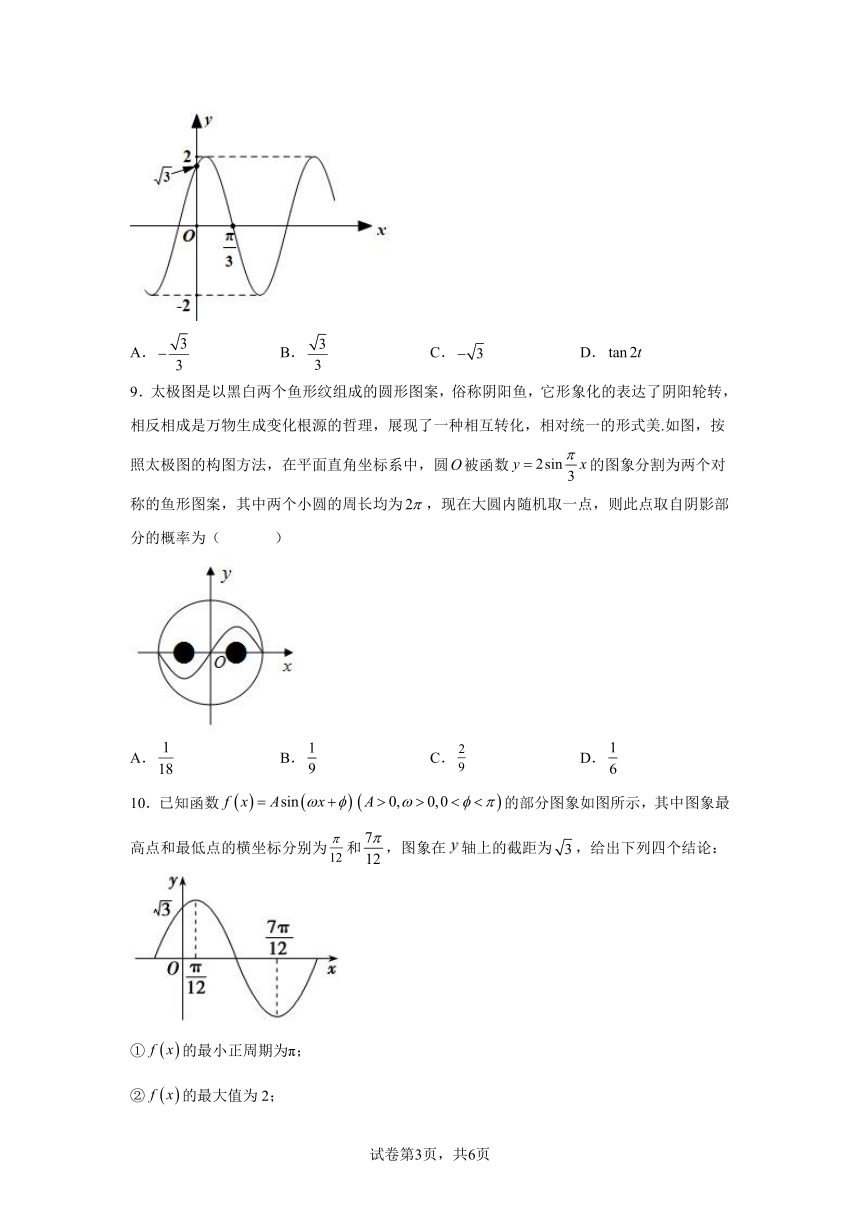
9.太极图是以黑白两个鱼形纹组成的圆形图案,俗称阴阳鱼,它形象化的表达了阴阳轮转,相反相成是万物生成变化根源的哲理,展现了一种相互转化,相对统一的形式美.如图,按照太极图的构图方法,在平面直角坐标系中,圆被函数的图象分割为两个对称的鱼形图案,其中两个小圆的周长均为,现在大圆内随机取一点,则此点取自阴影部分的概率为( )
A. B. C. D.
10.已知函数的部分图象如图所示,其中图象最高点和最低点的横坐标分别为和,图象在轴上的截距为,给出下列四个结论:
①的最小正周期为π;
②的最大值为2;
③;
④为奇函数.
其中正确结论的个数是( )
A.1 B.2 C.3 D.4
11.函数(其中的部分图象如图所示,则下列说法正确的是()
A.图象可由图象向左平移个单位得到
B.图象可由图象向左平移个单位得到
C.图象可由图象向右平移个单位得到
D.图象可由图象向右平移个单位得到
12.极坐标方程表示曲线的中心在( )
A.第四象限 B.第三象限 C.第二象限 D.第一象限
13.若,则( )
A. B.
C. D.
14.已知函数,且过点,则下列结论错误的是( )
A.
B.若时,将的图象向右平移个单位长度得到的图象关于原点对称
C.若,且最小正周期取最大值时,
D.若在上单调递增,则
二、多选题
15.已知函数,,则下列命题中正确的为( )
A.的最小正周期是,最大值
B.的单调增区间是,
C.
D.将的图象向右平移个单位可得函数的图象
三、双空题
16.双曲线的离心率为___________;渐近线为___________.
17.已知函数部分图象如图所示,则__________,为了得到偶函数的图象,至少要将函数的图象向右平移__________个单位长度.
四、填空题
18.已知,,,其中为正整数.设表示外接圆的面积,则______.
19.将函数图象上所有点的横坐标变为原来的倍(纵坐标不变),得到函数的图象,若是函数图象的一个对称中心,则的最大值为______.
20.函数(为常数,)在闭区间上的图象如图所示,则=__
21.将函数的图象上的所有点横坐标变为原来的,纵坐标不变,得到函数y=f(x)的图象,再将函数f(x)的图象向右平移个单位长度,向上平移1个单位,得到函数y=g(x)的图象,则=______.
五、解答题
22.已知函数的一个对称中心为,其图像上相邻两个最高点间的距离为.
(1)求函数的解析式;
(2)用“五点作图法”在给定的坐标系中作出函数在一个周期内的图像,并写出函数的单调递减区间.
试卷第页,共页
试卷第页,共页
参考答案:
1.D
【解析】
【分析】
使用诱导公式将函数化为的形式,根据函数图象平移规律得出答案.
【详解】
由
将的图象向右平移个单位长度,得
,
故选:D
【点睛】
本题考查了三角函数的恒等变换,函数图象变换,属于中档题.
2.A
【解析】
根据和的值的物理意义进行求解即可得结果.
【详解】
因为函数解析式中,,,,
所以函数的振幅为2,
周期为,所以频率为,初相为,
故选A.
【点睛】
该题考查的是有关函数解析式中的和的值的物理意义的问题,属于简单题目.
3.C
【解析】
【分析】
由求得的范围,由求得,再利用求得,得周期,结合周期可得最大值.
【详解】
由题意则为,则有,进而,
又或,因为大于0小于3,所以等于2,与,得:,则,
相邻2个零点的距离有两种和,则当为1010个与1011个的和时最大为.
故选:C.
4.C
【解析】
【分析】
由函数的部分图象求出、、和的值,写出的解析式,再得出的解析式.
【详解】
由函数,,的部分图象知,
,且,
解答,所以;
又,,,
所以,;
由知,;
所以;
所以.
故选:C.
5.B
【解析】
【详解】
因为,且==,
所以由=,知,即只需函数的图像向左平移个单位即可得函数的图像,故选B
6.A
【解析】
【分析】
利用余弦函数的五点作图求解即可
【详解】
令,得.∴该点坐标为.
故选A
【点睛】
本题考查”五点法”作函数y=Acos(ωx+φ)的图象,y=cosx的第一个周期内五个关键点:(0,1),(,0),(π,-1),(,0),(2π,1).
7.A
【解析】
利用函数的奇偶性和特殊点的函数值对选项进行排除即可.
【详解】
函数为奇函数,图象关于原点对称,故排除B、D,
当取从0的右侧趋近于0的正实数时,,函数值大于零,排除C,
故选:A.
【点睛】
本题考查函数图象的判断,利用函数的性质结合特殊值即可解决,属于基础题.
8.B
【解析】
由函数图象得函数,再根据函数的性质得方程在区间上所有的解共有2个且这2个解的和等于,进而得答案.
【详解】
解:由图可知,,
再把点代入可得,
所以,又,所以,
由五点作图法原理可得,所以,
故函数,
当时,,
令,得,
由图像可知方程在区间上所有的解共有2个,
且这2个解的和等于,即,
所以,
故选:B.
【点睛】
本题考查利用三角函数图象求解析式,函数的对称性,考查运算能力,是中档题.
9.C
【解析】
【分析】
先由小圆的周长,求出小圆半径,得出阴影部分面积;再由三角函数的周期求出大圆的直径,得出大圆面积,面积比即为所求概率.
【详解】
设小圆半径为,大圆半径为,
因为两个小圆的周长均为,所以,解得,
因此,阴影部分的面积为;
又函数的周期为,根据题中图像可得,,
所以,大圆的面积为:,
因此,在大圆内随机取一点,则此点取自阴影部分的概率为.
故选:C.
【点睛】
本题主要考查与面积有关的几何概型,其中涉及三角函数的周期,属于基础题型.
10.D
【解析】
【详解】
分析:利用三角函数的的图象,求解函数点最小正周期、的值,得到函数的解析式,即可判定,得到答案.
详解:由图象得,函数的最小正周期为,解得,
则,即,
又由,即,
所以,解得,即,
又由,即,所以,即,则函数的最大值为2,所以①②上正确的;
又由,所以③上正确的;
又由为奇函数,所以④是正确的,
所以正确结论的个数为4个,故选D.
点睛:本题主要考查了三角函数的图象与性质的综合应用,其中熟记三角函数的图象与性质,根据三角函数的图象,求得三角函数的解析式是解答的关键,着重考查了推理与运算能力,属于基础题.
11.B
【解析】
【详解】
由图像可知,即,解得,当时,,解得,根据函数的最大值是,所以函数的解析式是, ,根据左加右减,可知应向左平移2个单位,故选B.
12.A
【解析】
【分析】
化简得到,整理得到圆心为在第四象限,得到答案.
【详解】
,即,即.
故,圆心为在第四象限.
故选:.
【点睛】
本题考查了极坐标方程的转化,意在考查学生对于极坐标方程的理解和掌握.
13.D
【解析】
由可得,然后由诱导公式和同角三角函数的关系对选项进行逐一判断,即可得到答案.
【详解】
由可得,则
A. ,所以不正确.
B. ,所以不正确.
C. ,所以不做正确.
D. ,所以正确.
故选:D
【点睛】
本题考查诱导公式和同角三角函数的关系,属于基础题.
14.D
【解析】
【分析】
根据函数过点代入求出,再利用辅助角公式将函数化简,最后根据正弦函数的性质计算可得;
【详解】
解:因为函数过点,所以,所以.又因为,所以,故选项A正确;
所以,当时,,设将的图象向右平移个单位长度得到的图象,则,易知的图象关于原点对称,故选项B正确;
当时,解得.因为的最小正周期,所以时,最大,故选项C正确;
因为,所以
若在上单调递增,则,所以,故选项D错误,
故选:D.
15.ABCD
【解析】
直接利用三角函数的关系式的变换的应用,把函数的关系式变形成正弦型函数,进一步利用函数的性质求出函数的周期,最值,单调区间及利用函数的图象的平移变换判定、、、的结论.
【详解】
解:,
对于:函数的最小正周期为,
当,即时,函数的最大值为,故选项正确.
对于:令,解得,
所以函数的单调递增区间为,,故正确.
对于,故正确.
对于:函数的图象向右平移个单位得到,故正确.
故选:ABCD.
16.
【解析】
【分析】
根据双曲线方程求,再求离心率和渐近线方程.
【详解】
由双曲线方程可知,,则,
则双曲线的离心率,渐近线方程,即.
故答案为:;
17. 6
【解析】
【分析】
利用图象可得出函数的最小正周期,可得出的值,结合图象求得的值,然后将函数的图象向右平移个单位长度,求出的表达式,进而可求得的最小值,即为所求.
【详解】
由图象可知,函数的最小正周期为,,则,
由于函数的图象过点且在附近单调递增,所以,,可得,
,,,
假设将函数的图象向右平移个单位长度可得到偶函数的图象,
且,
所以,,解得,
,当时,取最小值.
故答案为:;.
18.
【解析】
【分析】
可设圆的外接圆方程为,将三点代入可求得圆的一般方程,求得半径,进而求得外接圆面积;还可采用极限思想求解
【详解】
方法一:设的外接圆方程为,将,,代入方程,则有,解得,三角形外接圆的方程为,半径满足,外接圆面积为,则;
方法二:当时,趋于原点,点趋于,此时圆心趋于,半径,从而所求圆的面积为
故答案为
【点睛】
本题考查三角形外接圆方程的求法,极限的简单计算,方法二中体现了极限思想的优越性,属于中档题
19.3
【解析】
【分析】
首先根据图象变换原则,写出,根据是函数图像的一个对称中心,得到等量关系式,从而求得结果.
【详解】
由题意可得,
∵是的一个对称中心,
∴,,解得,因为,
所以当时,取得最大值3.
故答案为:3.
【点睛】
该题考查的是有关三角函数的问题,涉及到的知识点有图象变换,根据函数图象的对称中心求参数,属于简单题目.
20.3
【解析】
【详解】
考查三角函数的周期知识
,,所以
21.2
【解析】
【分析】
利用函数y=Asin(ωx+φ)的图象变换规律,求得g(x)的解析式,从而求得g()的值.
【详解】
解:将函数的图象上的所有点横坐标变为原来的,纵坐标不变,得到函数y=f(x)=2sin(2x)的图象,
再将函数f(x)的图象向右平移个单位长度,向上平移1个单位,得到函数y=g(x)=2sin(2x)+1的图象,
则2sin1=2,
故答案为2.
【点睛】
本题主要考查函数y=Asin(ωx+φ)的图象变换规律,属于基础题.
22.(1);(2)
【解析】
【分析】
(1)因为的图像上相邻两个最高点的距离为,所以的最小正周期,由此得因为的对称中心为,因为的对称中心,,求得,即可得解;(2)由“五点作图法”找出函数在一个周期内的五个关键点,列表,描点,作图,即可得出函数的单调递减区间.
【详解】
(1)因为的图像上相邻两个最高点的距离为,
所以的最小正周期,
由和,可得
因为的对称中心为,
所以,,即,
又因为,所以,所以函数的解析式为.
(2)由“五点作图法”找出函数在一个周期内的五个关键点,列表如下:
由,可得,
所以函数的单调递减区间是.
【点睛】
本题考查三角函数性质,由周期,对称性得出解析式,考查五点作图法,是中档题.
试卷第页,共页
试卷第页,共页
一、单选题
1.要得到函数的图象,只需将的图象( )
A.向左平移个单位长度 B.向右平移个单位长度
C.向左平移个单位长度 D.向右平移个单位长度
2.的振幅、频率和初相分别为
A. B.
C. D.
3.已知且为整数,且,函数的图像如图所示,A、C,D是的图像与相邻的三个交点,与x轴交于相邻的两个交点O、B,若在区间上,有2020个零点,则的最大值为( )
A. B.
C. D.
4.若将函数g(x)图象上所有的点向左平移个单位长度得到函数f(x)的图象,已知函数f(x)=Asin(ωx+φ)的部分图象如图所示,则( )
A.g(x)=sin B.g(x)=sin
C.g(x)=sin2x D.g(x)=sin
5.函数的图像可以由函数的图像经过
A.向左平移个单位长度得到 B.向左平移个单位长度得到
C.向右平移个单位长度得到 D.向右平移个单位长度得到
6.用“五点法”作函数在一个周期内的图像时,第四个关键点的坐标是
A. B.
C. D.
7.函数的图象大致为( )
A. B.
C. D.
8.已知函数的部分图像如图所示,记关于的方程在区间上所有解的和为,则( )
A. B. C. D.
9.太极图是以黑白两个鱼形纹组成的圆形图案,俗称阴阳鱼,它形象化的表达了阴阳轮转,相反相成是万物生成变化根源的哲理,展现了一种相互转化,相对统一的形式美.如图,按照太极图的构图方法,在平面直角坐标系中,圆被函数的图象分割为两个对称的鱼形图案,其中两个小圆的周长均为,现在大圆内随机取一点,则此点取自阴影部分的概率为( )
A. B. C. D.
10.已知函数的部分图象如图所示,其中图象最高点和最低点的横坐标分别为和,图象在轴上的截距为,给出下列四个结论:
①的最小正周期为π;
②的最大值为2;
③;
④为奇函数.
其中正确结论的个数是( )
A.1 B.2 C.3 D.4
11.函数(其中的部分图象如图所示,则下列说法正确的是()
A.图象可由图象向左平移个单位得到
B.图象可由图象向左平移个单位得到
C.图象可由图象向右平移个单位得到
D.图象可由图象向右平移个单位得到
12.极坐标方程表示曲线的中心在( )
A.第四象限 B.第三象限 C.第二象限 D.第一象限
13.若,则( )
A. B.
C. D.
14.已知函数,且过点,则下列结论错误的是( )
A.
B.若时,将的图象向右平移个单位长度得到的图象关于原点对称
C.若,且最小正周期取最大值时,
D.若在上单调递增,则
二、多选题
15.已知函数,,则下列命题中正确的为( )
A.的最小正周期是,最大值
B.的单调增区间是,
C.
D.将的图象向右平移个单位可得函数的图象
三、双空题
16.双曲线的离心率为___________;渐近线为___________.
17.已知函数部分图象如图所示,则__________,为了得到偶函数的图象,至少要将函数的图象向右平移__________个单位长度.
四、填空题
18.已知,,,其中为正整数.设表示外接圆的面积,则______.
19.将函数图象上所有点的横坐标变为原来的倍(纵坐标不变),得到函数的图象,若是函数图象的一个对称中心,则的最大值为______.
20.函数(为常数,)在闭区间上的图象如图所示,则=__
21.将函数的图象上的所有点横坐标变为原来的,纵坐标不变,得到函数y=f(x)的图象,再将函数f(x)的图象向右平移个单位长度,向上平移1个单位,得到函数y=g(x)的图象,则=______.
五、解答题
22.已知函数的一个对称中心为,其图像上相邻两个最高点间的距离为.
(1)求函数的解析式;
(2)用“五点作图法”在给定的坐标系中作出函数在一个周期内的图像,并写出函数的单调递减区间.
试卷第页,共页
试卷第页,共页
参考答案:
1.D
【解析】
【分析】
使用诱导公式将函数化为的形式,根据函数图象平移规律得出答案.
【详解】
由
将的图象向右平移个单位长度,得
,
故选:D
【点睛】
本题考查了三角函数的恒等变换,函数图象变换,属于中档题.
2.A
【解析】
根据和的值的物理意义进行求解即可得结果.
【详解】
因为函数解析式中,,,,
所以函数的振幅为2,
周期为,所以频率为,初相为,
故选A.
【点睛】
该题考查的是有关函数解析式中的和的值的物理意义的问题,属于简单题目.
3.C
【解析】
【分析】
由求得的范围,由求得,再利用求得,得周期,结合周期可得最大值.
【详解】
由题意则为,则有,进而,
又或,因为大于0小于3,所以等于2,与,得:,则,
相邻2个零点的距离有两种和,则当为1010个与1011个的和时最大为.
故选:C.
4.C
【解析】
【分析】
由函数的部分图象求出、、和的值,写出的解析式,再得出的解析式.
【详解】
由函数,,的部分图象知,
,且,
解答,所以;
又,,,
所以,;
由知,;
所以;
所以.
故选:C.
5.B
【解析】
【详解】
因为,且==,
所以由=,知,即只需函数的图像向左平移个单位即可得函数的图像,故选B
6.A
【解析】
【分析】
利用余弦函数的五点作图求解即可
【详解】
令,得.∴该点坐标为.
故选A
【点睛】
本题考查”五点法”作函数y=Acos(ωx+φ)的图象,y=cosx的第一个周期内五个关键点:(0,1),(,0),(π,-1),(,0),(2π,1).
7.A
【解析】
利用函数的奇偶性和特殊点的函数值对选项进行排除即可.
【详解】
函数为奇函数,图象关于原点对称,故排除B、D,
当取从0的右侧趋近于0的正实数时,,函数值大于零,排除C,
故选:A.
【点睛】
本题考查函数图象的判断,利用函数的性质结合特殊值即可解决,属于基础题.
8.B
【解析】
由函数图象得函数,再根据函数的性质得方程在区间上所有的解共有2个且这2个解的和等于,进而得答案.
【详解】
解:由图可知,,
再把点代入可得,
所以,又,所以,
由五点作图法原理可得,所以,
故函数,
当时,,
令,得,
由图像可知方程在区间上所有的解共有2个,
且这2个解的和等于,即,
所以,
故选:B.
【点睛】
本题考查利用三角函数图象求解析式,函数的对称性,考查运算能力,是中档题.
9.C
【解析】
【分析】
先由小圆的周长,求出小圆半径,得出阴影部分面积;再由三角函数的周期求出大圆的直径,得出大圆面积,面积比即为所求概率.
【详解】
设小圆半径为,大圆半径为,
因为两个小圆的周长均为,所以,解得,
因此,阴影部分的面积为;
又函数的周期为,根据题中图像可得,,
所以,大圆的面积为:,
因此,在大圆内随机取一点,则此点取自阴影部分的概率为.
故选:C.
【点睛】
本题主要考查与面积有关的几何概型,其中涉及三角函数的周期,属于基础题型.
10.D
【解析】
【详解】
分析:利用三角函数的的图象,求解函数点最小正周期、的值,得到函数的解析式,即可判定,得到答案.
详解:由图象得,函数的最小正周期为,解得,
则,即,
又由,即,
所以,解得,即,
又由,即,所以,即,则函数的最大值为2,所以①②上正确的;
又由,所以③上正确的;
又由为奇函数,所以④是正确的,
所以正确结论的个数为4个,故选D.
点睛:本题主要考查了三角函数的图象与性质的综合应用,其中熟记三角函数的图象与性质,根据三角函数的图象,求得三角函数的解析式是解答的关键,着重考查了推理与运算能力,属于基础题.
11.B
【解析】
【详解】
由图像可知,即,解得,当时,,解得,根据函数的最大值是,所以函数的解析式是, ,根据左加右减,可知应向左平移2个单位,故选B.
12.A
【解析】
【分析】
化简得到,整理得到圆心为在第四象限,得到答案.
【详解】
,即,即.
故,圆心为在第四象限.
故选:.
【点睛】
本题考查了极坐标方程的转化,意在考查学生对于极坐标方程的理解和掌握.
13.D
【解析】
由可得,然后由诱导公式和同角三角函数的关系对选项进行逐一判断,即可得到答案.
【详解】
由可得,则
A. ,所以不正确.
B. ,所以不正确.
C. ,所以不做正确.
D. ,所以正确.
故选:D
【点睛】
本题考查诱导公式和同角三角函数的关系,属于基础题.
14.D
【解析】
【分析】
根据函数过点代入求出,再利用辅助角公式将函数化简,最后根据正弦函数的性质计算可得;
【详解】
解:因为函数过点,所以,所以.又因为,所以,故选项A正确;
所以,当时,,设将的图象向右平移个单位长度得到的图象,则,易知的图象关于原点对称,故选项B正确;
当时,解得.因为的最小正周期,所以时,最大,故选项C正确;
因为,所以
若在上单调递增,则,所以,故选项D错误,
故选:D.
15.ABCD
【解析】
直接利用三角函数的关系式的变换的应用,把函数的关系式变形成正弦型函数,进一步利用函数的性质求出函数的周期,最值,单调区间及利用函数的图象的平移变换判定、、、的结论.
【详解】
解:,
对于:函数的最小正周期为,
当,即时,函数的最大值为,故选项正确.
对于:令,解得,
所以函数的单调递增区间为,,故正确.
对于,故正确.
对于:函数的图象向右平移个单位得到,故正确.
故选:ABCD.
16.
【解析】
【分析】
根据双曲线方程求,再求离心率和渐近线方程.
【详解】
由双曲线方程可知,,则,
则双曲线的离心率,渐近线方程,即.
故答案为:;
17. 6
【解析】
【分析】
利用图象可得出函数的最小正周期,可得出的值,结合图象求得的值,然后将函数的图象向右平移个单位长度,求出的表达式,进而可求得的最小值,即为所求.
【详解】
由图象可知,函数的最小正周期为,,则,
由于函数的图象过点且在附近单调递增,所以,,可得,
,,,
假设将函数的图象向右平移个单位长度可得到偶函数的图象,
且,
所以,,解得,
,当时,取最小值.
故答案为:;.
18.
【解析】
【分析】
可设圆的外接圆方程为,将三点代入可求得圆的一般方程,求得半径,进而求得外接圆面积;还可采用极限思想求解
【详解】
方法一:设的外接圆方程为,将,,代入方程,则有,解得,三角形外接圆的方程为,半径满足,外接圆面积为,则;
方法二:当时,趋于原点,点趋于,此时圆心趋于,半径,从而所求圆的面积为
故答案为
【点睛】
本题考查三角形外接圆方程的求法,极限的简单计算,方法二中体现了极限思想的优越性,属于中档题
19.3
【解析】
【分析】
首先根据图象变换原则,写出,根据是函数图像的一个对称中心,得到等量关系式,从而求得结果.
【详解】
由题意可得,
∵是的一个对称中心,
∴,,解得,因为,
所以当时,取得最大值3.
故答案为:3.
【点睛】
该题考查的是有关三角函数的问题,涉及到的知识点有图象变换,根据函数图象的对称中心求参数,属于简单题目.
20.3
【解析】
【详解】
考查三角函数的周期知识
,,所以
21.2
【解析】
【分析】
利用函数y=Asin(ωx+φ)的图象变换规律,求得g(x)的解析式,从而求得g()的值.
【详解】
解:将函数的图象上的所有点横坐标变为原来的,纵坐标不变,得到函数y=f(x)=2sin(2x)的图象,
再将函数f(x)的图象向右平移个单位长度,向上平移1个单位,得到函数y=g(x)=2sin(2x)+1的图象,
则2sin1=2,
故答案为2.
【点睛】
本题主要考查函数y=Asin(ωx+φ)的图象变换规律,属于基础题.
22.(1);(2)
【解析】
【分析】
(1)因为的图像上相邻两个最高点的距离为,所以的最小正周期,由此得因为的对称中心为,因为的对称中心,,求得,即可得解;(2)由“五点作图法”找出函数在一个周期内的五个关键点,列表,描点,作图,即可得出函数的单调递减区间.
【详解】
(1)因为的图像上相邻两个最高点的距离为,
所以的最小正周期,
由和,可得
因为的对称中心为,
所以,,即,
又因为,所以,所以函数的解析式为.
(2)由“五点作图法”找出函数在一个周期内的五个关键点,列表如下:
由,可得,
所以函数的单调递减区间是.
【点睛】
本题考查三角函数性质,由周期,对称性得出解析式,考查五点作图法,是中档题.
试卷第页,共页
试卷第页,共页
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
