人教A版(2019)必修第一册过关斩将第三章3.4函数的应用(一)word版含答案
文档属性
| 名称 | 人教A版(2019)必修第一册过关斩将第三章3.4函数的应用(一)word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 780.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-19 10:55:09 | ||
图片预览



文档简介
人教A版(2019)必修第一册过关斩将第三章3.4函数的应用(一)
一、单选题
1.在函数y=|x|(x∈[-2,2])的图象上有一点P(t,|t|),此函数的图象与x轴、直线x=-2及x=t围成的图形(如图阴影部分)的面积为S,则S与t的函数关系图象可表示为
A. B. C. D.
2.已知函数其中.若对任意的都有,则实数的取值范围是( )
A. B.
C. D.
3.某种杂志原以每本2.5元的价格销售,可以售出8万本.据市场调查,杂志的单价每提高0.1元,销售量就可能减少2000本,若使提价后的销售总收入不低于20万元,则提价后的价格至多是( )
A.4元 B.5元 C.3元 D.6元
4.视力检测结果有两种记录方式,分别是小数记录与五分记录,其部分数据如下表:
小数记录
五分记录
现有如下函数模型:①,②,表示小数记录数据,表示五分记录数据,请选择最合适的模型解决如下问题:小明同学检测视力时,医生告诉他的视力为,则小明同学的小数记录数据为(附,,)( )A. B. C. D.
5.已知函数的最大值为1,则的取值范围为
A. B. C. D.
6.英国物理学家、数学家牛顿曾提出在常温环境下温度变化的冷却模型:如果物体的初始温度是,环境温度是,那么经过小时后物体的温度将满足.通过实验观察发现,在的室温下,一块从冰箱中取出的的冻肉经过小时后温度升至,在相同的环境下利用牛顿冷却模型计算:温度为的水,冷却到,大约经过的时间为( )(忽略体积等其它因素的影响)
A.小时 B.小时 C.小时 D.小时
7.已知函数在区间上有最小值,则实数的值为( )
A. B. C. D.或
8.下列四个图象中,与所给三个事件吻合最好的顺序为( )
①我离开家不久,发现自己把作业本忘在家里了,于是立刻返回家里取了作业本再上学;
②我骑着车一路以常速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间;
③我出发后,心情轻松,缓缓行进,后来为了赶时间开始加速.
其中y表示离开家的距离,t表示所用时间.
A.④①② B.③①② C.②①④ D.③②①
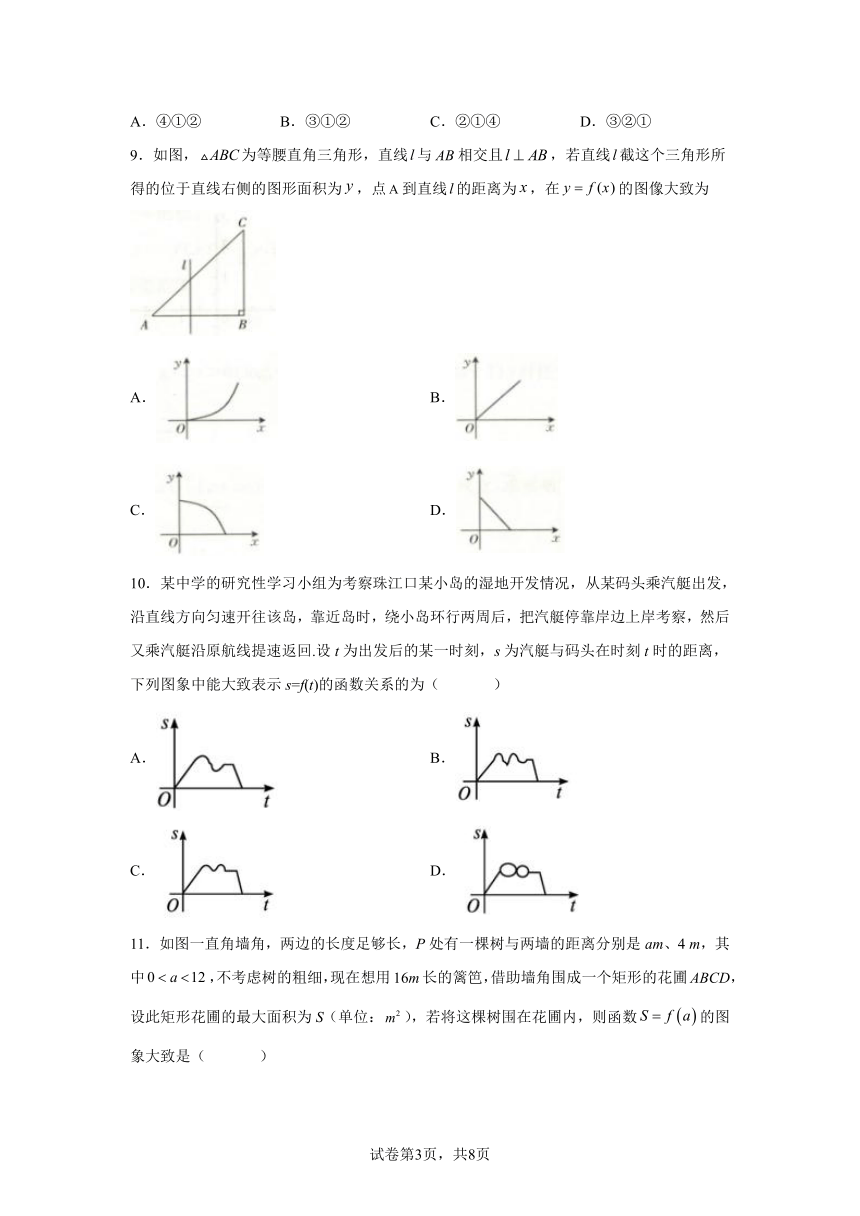
9.如图,为等腰直角三角形,直线与相交且,若直线截这个三角形所得的位于直线右侧的图形面积为,点到直线的距离为,在的图像大致为
A. B.
C. D.
10.某中学的研究性学习小组为考察珠江口某小岛的湿地开发情况,从某码头乘汽艇出发,沿直线方向匀速开往该岛,靠近岛时,绕小岛环行两周后,把汽艇停靠岸边上岸考察,然后又乘汽艇沿原航线提速返回.设t为出发后的某一时刻,s为汽艇与码头在时刻t时的距离,下列图象中能大致表示s=f(t)的函数关系的为( )
A. B.
C. D.
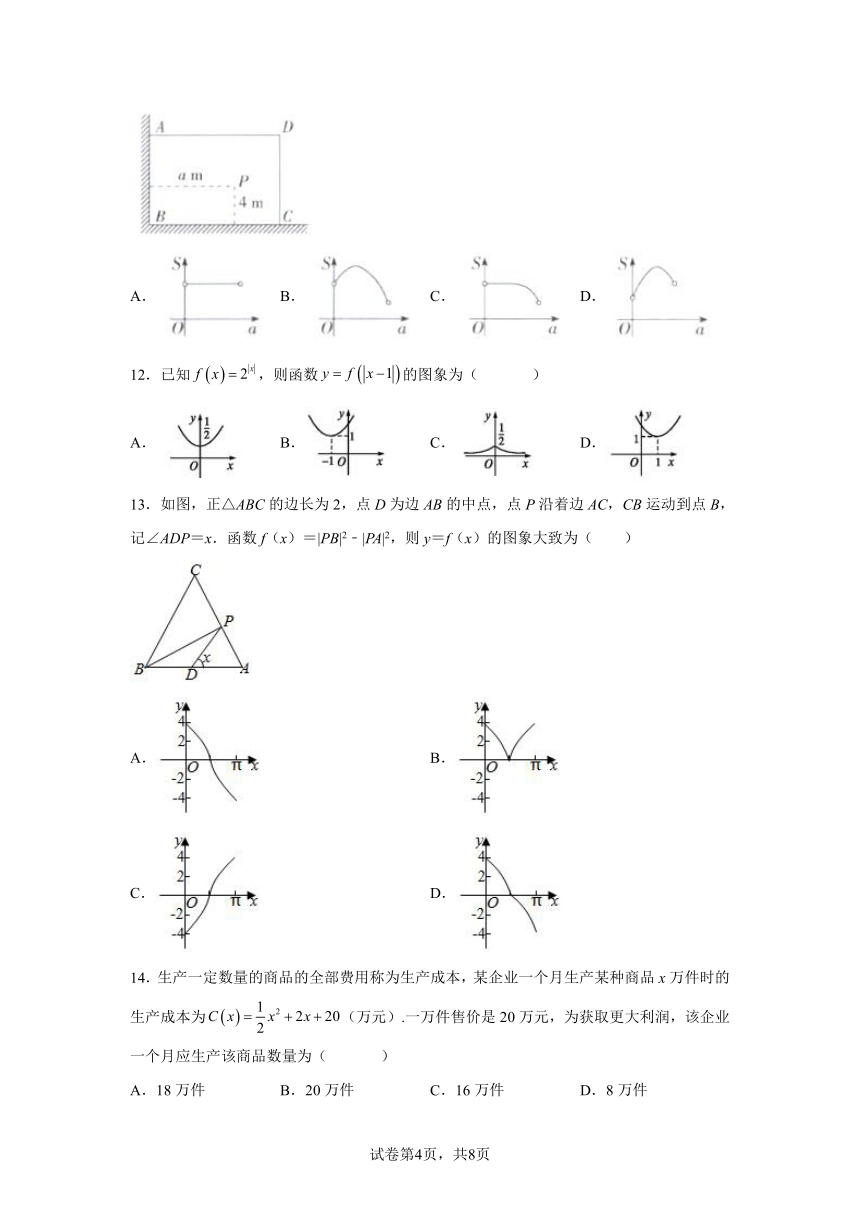
11.如图一直角墙角,两边的长度足够长,P处有一棵树与两墙的距离分别是am、4 m,其中,不考虑树的粗细,现在想用16m长的篱笆,借助墙角围成一个矩形的花圃ABCD,设此矩形花圃的最大面积为S(单位:),若将这棵树围在花圃内,则函数的图象大致是( )
A. B. C. D.
12.已知,则函数的图象为( )
A. B. C. D.
13.如图,正△ABC的边长为2,点D为边AB的中点,点P沿着边AC,CB运动到点B,记∠ADP=x.函数f(x)=|PB|2﹣|PA|2,则y=f(x)的图象大致为( )
A. B.
C. D.
14.生产一定数量的商品的全部费用称为生产成本,某企业一个月生产某种商品x万件时的生产成本为(万元).一万件售价是20万元,为获取更大利润,该企业一个月应生产该商品数量为( )
A.18万件 B.20万件 C.16万件 D.8万件
二、多选题
15.(多选)血药浓度(Plasma Concentration)是指药物吸收后在血浆内的总浓度.药物在人体内发挥治疗作用时,该药物的血药浓度应介于最低有效浓度和最低中毒浓度之间.已知成人单次服用1单位某药物后,体内血药浓度及相关信息如图所示:
根据图中提供的信息,下列关于成人使用该药物的说法中,正确的是( )
A.首次服用该药物1单位约10分钟后,药物发挥治疗作用
B.每次服用该药物1单位,两次服药间隔小于2小时,一定会产生药物中毒
C.每间隔5.5小时服用该药物1单位,可使药物持续发挥治疗作用
D.首次服用该药物1单位3小时后,再次服用该药物1单位,不会发生药物中毒
16.为预防秋冬季流感,学校每天定时对教室进行喷洒消毒.教室内每立方米空气中的含药量(单位:)随时间(单位:)的变化情况如图所示:在药物释放过程中,与成正比;药物释放完毕后,与的函数关系式为(为常数),则( )
A.当时,
B.当时,
C.时,教室内每立方米空气中的含药量高于
D.教室内每立方米空气中的含药量高于的持续时间超过90分钟.
三、填空题
17.“好酒也怕巷子深”,许多著名品牌是通过广告宣传进入消费者视线的.已知某品牌商品靠广告销售的收入R与广告费A之间满足关系R=a(a为正常数),广告效应为D=a-A.那么精明的商人为了取得最大广告效应,投入广告费应为________.
18.某城市出租车收费方法如下:起步价为6元,可行驶3km(含3km),行驶3km到10km(含10km)每增加1km车费增加0.5元,超过10km每增加1km车费增加0.8元,不足1km均按1km计算,若某人乘出租车行驶了11.5km,那么他应该付车费是_________元.
19.如图所示,学校要建造一面靠墙(墙足够长)的2个面积相同的矩形花圃,如果可供建造围墙的材料总长是60m,要所建造的每个花圃的面积最大,则宽应为___________m.
四、解答题
20.已知函数
(1)求的值;
(2)若,求实数a的值.
21.某物流公司欲将一批海产品从A地运往B地,现有汽车、火车、飞机三种运输工具可供选择,这三种工具的主要参考数据如下:
运输工具 途中速度() 途中费用(元/) 装卸时间() 装卸费用(元/)
汽车 50 80 2 200
火车 100 40 3 400
飞机 200 200 3 800
若这批海产品在运输过程中的损耗为300元/,问采用哪种运输方式比较好,即运输过程中的费用与损耗之和最小.
22.某商品在近30天内每件的销售价格(元)与时间(天)的函数关系是,该商品的日销售量(件)与时间(天)的函数关系是.求这种商品的日销售金额的最大值,并指出日销售金额最大的一天是30天中的第几天?(注:日销售金额=日销售价格×日销售量)
23.建造一间地面面积为12的背面靠墙的猪圈, 底面为长方形的猪圈正面的造价为120元/, 侧面的造价为80元/, 屋顶造价为1120元. 如果墙高3, 且不计猪圈背面的费用, 问怎样设计能使猪圈的总造价最低, 最低总造价是多少元
24.已知函数.
(1)若,求的值域;
(2)若对于任意的实数,都有恒成立,求实数的取值范围.
25.已知函数(其中a为常数).
(1)当a=1时,求f(x)在上的值域;
(2)若当x∈[0,1]时,不等式恒成立,求实数a的取值范围;
(3)设,是否存在正数a,使得对于区间上的任意三个实数m,n,p,都存在以f(g(m)),f(g(n)),f(g(p))为边长的三角形?若存在,试求出这样的a的取值范围;若不存在,请说明理由.
26.为了抗击新型冠状病毒肺炎,某医药公司研究出一种消毒剂,据实验表明,该药物释放量(单位:)与时间(单位:)的函数关系为,当消毒后,测量得药物释放量等于;而实验表明,当药物释放量小于对人体无害.
(1)求的值;
(2)若使用该消毒剂对房间进行消毒,求对人体有害的时间有多长?
27.随着我国经济发展 医疗消费需求增长 人们健康观念转变以及人口老龄化进程加快等因素的影响,医疗器械市场近年来一直保持了持续增长的趋势.某医疗器械公司为了进一步增加市场竞争力,计划改进技术生产某产品.已知生产该产品的年固定成本为万元,最大产能为台.每生产台,需另投入成本万元,且由市场调研知,该产品每台的售价为200万元,且全年内生产的该产品当年能全部销售完.
(1)写出年利润万元关于年产量台的函数解析式(利润=销售收入-成本);
(2)当该产品的年产量为多少时,公司所获利润最大?最大利润是多少?
试卷第页,共页
试卷第页,共页
参考答案:
1.B
【解析】
【详解】
当t<0时,S=,其图象是开口向下的抛物线,顶点坐标是(0,);当时,S=,其图象是开口向上的抛物线,顶点坐标是(0,).所以B满足要求.
考点:图象法表示函数.
2.B
【解析】
根据增函数的定义可得在上为增函数,再根据分段函数的单调性列式可解得结果.
【详解】
因为对任意的都有,所以,即,所以在上为增函数,
所以,因为,所以.
故选:B
【点睛】
关键点点睛:抓住分段函数分界点的函数值的大小关系是解题关键,属于基础题.
3.A
【解析】
设提价后价格是元(),求出销售量得总收入,列不等式求解.
【详解】
设提价后价格是元(),则销售量为(万本)
销售总收入为,
由,得,∴
∴提价后至多为每本4元.
故选:A.
【点睛】
关键点点睛:本题考查函数的应用,解题时需引入参数,可根据已知函数模型列出函数或不等式求解.本题要注意的单位要统一,销售收入是以元为单位还是以万元为单位要一致,否则易出错.
4.B
【解析】
【分析】
根据表格中可知函数的单调性,可选择合适的函数模型,然后令,解方程即可得解.
【详解】
由表格中的数据可知,函数单调递增,故合适的函数模型为,
令,解得.
故选:B.
5.B
【解析】
【分析】
根据题意原函数是一个周期函数,以2018为周期的函数,根据二次函数的对称性得到结果即可.
【详解】
根据题意原函数是一个周期函数,以2018为周期的函数,,
根据二次函数的图形的特点得到,最大值在x=0或者x=2018处取得,f(0)=1,对称轴为,故只需要.
故答案为B.
【点睛】
本题考查了函数的周期性和二次函数的图像的性质和最值问题,二次函数的最值和轴与区间的位置关系是有联系的.
6.D
【解析】
【分析】
利用题中的条件先计算出的值,再代入数据即可得出结果.
【详解】
由题意知:
,
,
即,
等式两边同时取对数得,
,
则;
设温度为的水冷却到所经过的时间为,
则,
即,
解得;
故选:D.
7.D
【解析】
【分析】
根据一次函数的图象与性质,分类讨论列出方程,即可求解.
【详解】
当时,函数,显然不符合题意;
当时,函数为单调递减函数,所以,解得;
当时,函数为单调递增函数,所以,解得.
综上可得,实数的值为或.
故选:D.
8.A
【解析】
【分析】
根据三个事件的特征,分析离家距离的变化情况,选出符合事件的图像.
【详解】
对于事件①,中途返回家,离家距离为0,故图像④符合;
对于事件②,堵车中途耽搁了一些时间,中间有段时间离家距离不变,故图像①符合;
对于事件③,前面速度慢,后面赶时间加快速度,故图像②符合;
故选:A.
9.C
【解析】
【详解】
设AB=a,则y=a2 x2= x2+a2,
其图象为抛物线的一段,开口向下,顶点在y轴上方,
本题选择C选项.
10.C
【解析】
【分析】
因为该汽艇沿直线方向匀速开往改岛,靠近岛时,绕小岛环行两周后,把汽艇停靠岸边考查,然后又乘汽艇沿原航线提速返回,由此即可求出答案.
【详解】
解:因为该汽艇中途停靠岸边考察,此时间段不变,绕小岛环行两周,汽艇与码头的距离最小值,不会低于靠近海岛时的距离,故排除,,
因为为汽艇与码头在时刻的距离,其图象能表示的函数关系,而图表示的不是函数关系,故排除.
故选:.
【点睛】
本题函数图象的应用,同学们要注意分析其中得“关键点”,还要善于分析各图象的变化趋势,属于基础题.
11.C
【解析】
为求矩形面积的最大值,可先将其面积表达出来,又要注意点在长方形内,所以要注意分析自变量的取值范围,并以自变量的限制条件为分类标准进行分类讨论.
【详解】
解:设长为,则长为
又因为要将点围在矩形内,
则矩形的面积为,
当时,当且仅当时,
当时,
分段画出函数图形可得其形状与接近
故选:.
【点睛】
解决本题的关键是将的表达式求出来,结合自变量的取值范围,分类讨论后求出的解析式,属于基础题.
12.D
【解析】
【分析】
将函数的解析式表示为分段函数,进而可判断出函数的图象.
【详解】
,则,
因此,函数的图象如D选项中的图象所示.
故选:D.
【点睛】
本题考查指数型函数图象的识别,化简函数解析式是判断的关键,属于基础题.
13.A
【解析】
【分析】
根据题意,结合图形,分析区间(0,)和(,π)上f(x)的符号,再分析f(x)的对称性,排除BCD,即可得答案.
【详解】
根据题意,f(x)=|PB|2﹣|PA|2,∠ADP=x.
在区间(0,)上,P在边AC上,|PB|>|PA|,则f(x)>0,排除C;
在区间(,π)上,P在边BC上,|PB|<|PA|,则f(x)<0,排除B,
又由当x1+x2=π时,有f(x1)=﹣f(x2),f(x)的图象关于点(,0)对称,排除D,
故选:A
14.A
【解析】
【分析】
先求得利润的表达式,然后结合二次函数的性质求得利润取得最大值时对应的生产数量.
【详解】
利润
.
所以当时,L(x)有最大值.
故选:A
【点睛】
本小题主要考查二次函数模型的应用,属于基础题.
15.ABC
【解析】
【分析】
通过图象判断选项ABC正确;第一次服用该药物1单位3小时后与第2次服用该药物1单位1小时后,一定会发生药物中毒,故选项D错误.
【详解】
从图象中可以看出,首次服用该药物1单位约10分钟后药物发挥治疗作用,故选项A正确;
根据图象可知,首次服用该药物1单位约1小时后的血药浓度达到最大值,由图象可知两次服药间隔小于2小时,一定会产生药物中毒,故选项B正确;
服药5.5小时时,血药浓度等于最低有效浓度,此时再服药,血药浓度增加,可使药物持续发挥治疗作用,故选项C正确;
第一次服用该药物1单位3小时后与第2次服用该药物1单位1小时后,血药浓度之和大于最低中毒浓度,因此一定会发生药物中毒,故选项D错误.
故选:ABC.
16.ABC
【解析】
【分析】
利用待定系数法求出函数解析式,并根据函数解析式计算药含量变化情况得答案.
【详解】
解:当时,设,则,故,则,故正确;
当时,把代入,可得,则,即,故正确;
当时,,故正确;
当时,由,得,当时,由,得,即,
分钟,故错误.
故选:.
17.
【解析】
【分析】
先将D=a-A进行配方,求出D取最大值时的A的值,即可得出结论.
【详解】
由题意得,D=a-A=-(-+,且A≥0,∴当=,即A=时,D最大,故答案为.
【点睛】
本题考查了二次函数最值的求法,关键是对解析式进行配方即得函数的最值以及对应的自变量的值.
18.11.1
【解析】
【分析】
将出租车行驶了11.5km,分为三部分计费:出租车行驶3km,需要6元,3km到10km,需要元,再行驶1.5km,需要元,从而可得结果.
【详解】
根据题意,行驶10km时,付车费,再行驶1.5km,增加车费1.6元,则应付车费元,
故答案为:11.1
【点睛】
此题考查分段函数的应用,考查分析问题的能力,属于基础题.
19.10
【解析】
【分析】
建立面积的函数关系式,利用二次函数求出取最大值时的x.
【详解】
设每个花圃的面积的面积为y,则
因为,
所以当时,y最大.
故答案为:10.
【点睛】
数学建模是高中数学六大核心素养之一,在高中数学中,应用题是常见考查形式:
(1)求解应用性问题时,首先要弄清题意,分清条件和结论,抓住关键词和量,理顺数量关系,然后将文字语言转化成数学语言,建立相应的数学模型;
(2)求解应用性问题时,不仅要考虑函数本身的定义域,还要结合实际问题理解自变量的取值范围.
20.(1);(2).
【解析】
(1)代入求值即可;
(2)对进行讨论,令解出即可.
【详解】
解:函数,
,
,
;
,
当时,,
解得:,不成立;
当时,,
解得:,成立;
当时,,
此方程无解,
综上所述:实数a的值为.
21.当时,汽车总费用最小;当时,火车总费用最小;当时,飞机总费用最小(其中表示运输路程)
【解析】
【分析】
根据路程分别求出三种运输工具的费用与损耗之和(即途中费用+装卸费用+运输损耗),然后比较可得.
【详解】
设路程为,汽车、火车、飞机三种运输工具的费用与损耗之和分别为,则
,
,
,
从三条直线的斜率和纵截距,它们的图象大致位置如图所示,
时,,时,,
所以当时,最小,汽车总费用最小,当时,最小,火车总费用最小,当时,最小,飞机总费用最小.
答:当时,汽车总费用最小;当时,火车总费用最小;当时,飞机总费用最小(其中表示运输路程)
【点睛】
本题考查函数模型的应用,解题关键求出三个函数式,然后比较它们的大小.
22.元;第25天
【解析】
【分析】
分情况讨论即可获得日销售金额y关于时间t的函数关系式,根据分段函数不同段上的表达式,分别求最大值取较大者即可解答.
【详解】
∵日销售金额,
∴
.
当,,时,(元);
当,,时.(元);
∵,∴第25天日销售金额最大,(元).
【点睛】
本题考查分段函数的应用,考查分类讨论的思想、二次函数求最值得方法以及问题转化的能力,属于中档题.
23.当猪圈正面底边为4米侧面底边为3米时, 总造价最低为4000元.
【解析】
【详解】
试题分析:解:设猪圈底面正面的边长为xm,则其侧面边长为m---(2分)那么猪圈的总造价y=3x×120+3××80×2+112=360x++1120,---(3分)因为360x+≥2 =2880,---(2分)当且仅当360x=,即x=4时取“=”,(1分)所以当猪圈正面底边为4米侧面底边为3米时,总造价最低为4000元
考点:基本不等式在最值问题中的应用
点评:本小题主要考基本不等式在最值问题中的应用等基础知识,观察函数特点:为一个含有两个部分,这两部分的积为一个常数,求和的最值,所以利用基本不等式求最值.
24.(1);(2).
【解析】
【分析】
(1)当时,可得,利用二次函数的基本性质可求得函数的值域;
(2)分析可知,对于任意的实数,恒成立,对实数的取值进行分类讨论,可得出关于实数的不等式组,由此可求得实数的取值范围.
【详解】
(1)当时,,
因为,故,所以函数的值域为;
(2)由题意恒成立,
恒成立,
所以,只要恒成立即可,即恒成立.
①当时,恒成立,符合题意;
②当时,则有,解得.
综上所述:.
25.(1)[2,] (2)-<a<(3)(-,-)∪(,)
【解析】
【分析】
(1)当a=1时,f(x)=x+,结合对勾函数的图象和性质,可得f(x)在[,2]上的值域;
(2)若不等式f(2x)<2x++4在[0,1]上恒成立,即a<-2(2x)2+1+2x在[0,1]上恒成立,令t=2x,则t∈[1,2],y=-2t2+t+1,结合二次函数的图象和性质,求出函数的最小值,可得实数a的取值范围;
(3)换元,原问题等价于求实数a的范围,使得函数在给定的区间上,恒有2ymin>ymax
【详解】
解:(1)函数,
当a=1时,f(x)=x+,导数为f′(x)=1-=,
f(x)在[,1]上为减函数,在[1,2]上为增函数,
∴当x=,或x=2时,函数最最大值,当x=1时,函数取最小值2,
故f(x)在[,2]上的值域为[2,];
(2)若不等式f(2x)<2x++4在[0,1]上恒成立,
即2x+<2x++4在[0,1]上恒成立,即a2<1+4 2x在[0,1]上恒成立,
1+4 2x在[0,1]递增,可得最小值为1+4=5,即a2<5,解得-<a<;
(3)设t=g(x)==-1+在x∈[0,]递减,可得t∈[,1],则y=t+,
原问题转化为求实数a的取值范围,使得y在区间[,1]上,恒有2ymin>ymax.
讨论:①当0<a2≤时,y=t+在[,1]上递增,∴ymin=3a2+,ymax=a2+1,
由2ymin>ymax得a2>,∴<a≤;或-≤a<-;
②当<a2≤时,y=t+在[,|a|]上单调递减,在[|a|,1]上单调递增,
∴ymin=2|a|,ymax=max{3a2+,a2+1}=a2+1,
由2ymin>ymax得2-<|a|<2+,∴<|a|≤;
③当<|a|<1时,y=t+在[,|a|]上单调递减,在[|a|,1]上单调递增,
∴ymin=2|a|,ymax=max{3a2+,a2+1}=3a2+,
由2ymin>ymax得<|a|<,∴<|a|<1;
④当|a|≥1时,y=t+在[,1]上单调递减,∴ymin=a2+1,ymax=3a2+,
由2ymin>ymax得a2<,∴1≤a2<;
综上,a的取值范围是(-,-)∪(,).
【点睛】
本题主要考查了函数的基本性质的应用问题,其中解答中熟练应用函数的单调性与函数的奇偶性,合理分类讨论求解函数的最值是解答的关键,着重考查了分类讨论思想和转化思想的应用,以及分析问题和解答问题的能力,属于中档试题.
26.(1);(2).
【解析】
【分析】
(1)把代入即可求得的值;
(2)根据,通过分段讨论列出不等式组,从而求解.
【详解】
(1)由题意可知,故;
(2)因为,所以,
又因为时,药物释放量对人体有害,
所以或,解得或,所以,
由,故对人体有害的时间为.
27.(1);(2)该产品的年产量为台时,公司所获利润最大,最大利润是万元.
【解析】
【分析】
(1)根据年利润等于总收入减去固定成本万再减去另投入成本,写成分段函数的形式即可;
(2)分别由二次函数的性质以及基本不等式求出分段函数各段的最大值,再比较取最大值即可求解.
【详解】
(1)由题意可得:
当时,
;
当时,,
所以
(2)若,,
所以当时,万元.
若,,
当且仅当时,即时,万元.
所以该产品的年产量为台时,公司所获利润最大,最大利润是万元.
试卷第页,共页
试卷第页,共页
一、单选题
1.在函数y=|x|(x∈[-2,2])的图象上有一点P(t,|t|),此函数的图象与x轴、直线x=-2及x=t围成的图形(如图阴影部分)的面积为S,则S与t的函数关系图象可表示为
A. B. C. D.
2.已知函数其中.若对任意的都有,则实数的取值范围是( )
A. B.
C. D.
3.某种杂志原以每本2.5元的价格销售,可以售出8万本.据市场调查,杂志的单价每提高0.1元,销售量就可能减少2000本,若使提价后的销售总收入不低于20万元,则提价后的价格至多是( )
A.4元 B.5元 C.3元 D.6元
4.视力检测结果有两种记录方式,分别是小数记录与五分记录,其部分数据如下表:
小数记录
五分记录
现有如下函数模型:①,②,表示小数记录数据,表示五分记录数据,请选择最合适的模型解决如下问题:小明同学检测视力时,医生告诉他的视力为,则小明同学的小数记录数据为(附,,)( )A. B. C. D.
5.已知函数的最大值为1,则的取值范围为
A. B. C. D.
6.英国物理学家、数学家牛顿曾提出在常温环境下温度变化的冷却模型:如果物体的初始温度是,环境温度是,那么经过小时后物体的温度将满足.通过实验观察发现,在的室温下,一块从冰箱中取出的的冻肉经过小时后温度升至,在相同的环境下利用牛顿冷却模型计算:温度为的水,冷却到,大约经过的时间为( )(忽略体积等其它因素的影响)
A.小时 B.小时 C.小时 D.小时
7.已知函数在区间上有最小值,则实数的值为( )
A. B. C. D.或
8.下列四个图象中,与所给三个事件吻合最好的顺序为( )
①我离开家不久,发现自己把作业本忘在家里了,于是立刻返回家里取了作业本再上学;
②我骑着车一路以常速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间;
③我出发后,心情轻松,缓缓行进,后来为了赶时间开始加速.
其中y表示离开家的距离,t表示所用时间.
A.④①② B.③①② C.②①④ D.③②①
9.如图,为等腰直角三角形,直线与相交且,若直线截这个三角形所得的位于直线右侧的图形面积为,点到直线的距离为,在的图像大致为
A. B.
C. D.
10.某中学的研究性学习小组为考察珠江口某小岛的湿地开发情况,从某码头乘汽艇出发,沿直线方向匀速开往该岛,靠近岛时,绕小岛环行两周后,把汽艇停靠岸边上岸考察,然后又乘汽艇沿原航线提速返回.设t为出发后的某一时刻,s为汽艇与码头在时刻t时的距离,下列图象中能大致表示s=f(t)的函数关系的为( )
A. B.
C. D.
11.如图一直角墙角,两边的长度足够长,P处有一棵树与两墙的距离分别是am、4 m,其中,不考虑树的粗细,现在想用16m长的篱笆,借助墙角围成一个矩形的花圃ABCD,设此矩形花圃的最大面积为S(单位:),若将这棵树围在花圃内,则函数的图象大致是( )
A. B. C. D.
12.已知,则函数的图象为( )
A. B. C. D.
13.如图,正△ABC的边长为2,点D为边AB的中点,点P沿着边AC,CB运动到点B,记∠ADP=x.函数f(x)=|PB|2﹣|PA|2,则y=f(x)的图象大致为( )
A. B.
C. D.
14.生产一定数量的商品的全部费用称为生产成本,某企业一个月生产某种商品x万件时的生产成本为(万元).一万件售价是20万元,为获取更大利润,该企业一个月应生产该商品数量为( )
A.18万件 B.20万件 C.16万件 D.8万件
二、多选题
15.(多选)血药浓度(Plasma Concentration)是指药物吸收后在血浆内的总浓度.药物在人体内发挥治疗作用时,该药物的血药浓度应介于最低有效浓度和最低中毒浓度之间.已知成人单次服用1单位某药物后,体内血药浓度及相关信息如图所示:
根据图中提供的信息,下列关于成人使用该药物的说法中,正确的是( )
A.首次服用该药物1单位约10分钟后,药物发挥治疗作用
B.每次服用该药物1单位,两次服药间隔小于2小时,一定会产生药物中毒
C.每间隔5.5小时服用该药物1单位,可使药物持续发挥治疗作用
D.首次服用该药物1单位3小时后,再次服用该药物1单位,不会发生药物中毒
16.为预防秋冬季流感,学校每天定时对教室进行喷洒消毒.教室内每立方米空气中的含药量(单位:)随时间(单位:)的变化情况如图所示:在药物释放过程中,与成正比;药物释放完毕后,与的函数关系式为(为常数),则( )
A.当时,
B.当时,
C.时,教室内每立方米空气中的含药量高于
D.教室内每立方米空气中的含药量高于的持续时间超过90分钟.
三、填空题
17.“好酒也怕巷子深”,许多著名品牌是通过广告宣传进入消费者视线的.已知某品牌商品靠广告销售的收入R与广告费A之间满足关系R=a(a为正常数),广告效应为D=a-A.那么精明的商人为了取得最大广告效应,投入广告费应为________.
18.某城市出租车收费方法如下:起步价为6元,可行驶3km(含3km),行驶3km到10km(含10km)每增加1km车费增加0.5元,超过10km每增加1km车费增加0.8元,不足1km均按1km计算,若某人乘出租车行驶了11.5km,那么他应该付车费是_________元.
19.如图所示,学校要建造一面靠墙(墙足够长)的2个面积相同的矩形花圃,如果可供建造围墙的材料总长是60m,要所建造的每个花圃的面积最大,则宽应为___________m.
四、解答题
20.已知函数
(1)求的值;
(2)若,求实数a的值.
21.某物流公司欲将一批海产品从A地运往B地,现有汽车、火车、飞机三种运输工具可供选择,这三种工具的主要参考数据如下:
运输工具 途中速度() 途中费用(元/) 装卸时间() 装卸费用(元/)
汽车 50 80 2 200
火车 100 40 3 400
飞机 200 200 3 800
若这批海产品在运输过程中的损耗为300元/,问采用哪种运输方式比较好,即运输过程中的费用与损耗之和最小.
22.某商品在近30天内每件的销售价格(元)与时间(天)的函数关系是,该商品的日销售量(件)与时间(天)的函数关系是.求这种商品的日销售金额的最大值,并指出日销售金额最大的一天是30天中的第几天?(注:日销售金额=日销售价格×日销售量)
23.建造一间地面面积为12的背面靠墙的猪圈, 底面为长方形的猪圈正面的造价为120元/, 侧面的造价为80元/, 屋顶造价为1120元. 如果墙高3, 且不计猪圈背面的费用, 问怎样设计能使猪圈的总造价最低, 最低总造价是多少元
24.已知函数.
(1)若,求的值域;
(2)若对于任意的实数,都有恒成立,求实数的取值范围.
25.已知函数(其中a为常数).
(1)当a=1时,求f(x)在上的值域;
(2)若当x∈[0,1]时,不等式恒成立,求实数a的取值范围;
(3)设,是否存在正数a,使得对于区间上的任意三个实数m,n,p,都存在以f(g(m)),f(g(n)),f(g(p))为边长的三角形?若存在,试求出这样的a的取值范围;若不存在,请说明理由.
26.为了抗击新型冠状病毒肺炎,某医药公司研究出一种消毒剂,据实验表明,该药物释放量(单位:)与时间(单位:)的函数关系为,当消毒后,测量得药物释放量等于;而实验表明,当药物释放量小于对人体无害.
(1)求的值;
(2)若使用该消毒剂对房间进行消毒,求对人体有害的时间有多长?
27.随着我国经济发展 医疗消费需求增长 人们健康观念转变以及人口老龄化进程加快等因素的影响,医疗器械市场近年来一直保持了持续增长的趋势.某医疗器械公司为了进一步增加市场竞争力,计划改进技术生产某产品.已知生产该产品的年固定成本为万元,最大产能为台.每生产台,需另投入成本万元,且由市场调研知,该产品每台的售价为200万元,且全年内生产的该产品当年能全部销售完.
(1)写出年利润万元关于年产量台的函数解析式(利润=销售收入-成本);
(2)当该产品的年产量为多少时,公司所获利润最大?最大利润是多少?
试卷第页,共页
试卷第页,共页
参考答案:
1.B
【解析】
【详解】
当t<0时,S=,其图象是开口向下的抛物线,顶点坐标是(0,);当时,S=,其图象是开口向上的抛物线,顶点坐标是(0,).所以B满足要求.
考点:图象法表示函数.
2.B
【解析】
根据增函数的定义可得在上为增函数,再根据分段函数的单调性列式可解得结果.
【详解】
因为对任意的都有,所以,即,所以在上为增函数,
所以,因为,所以.
故选:B
【点睛】
关键点点睛:抓住分段函数分界点的函数值的大小关系是解题关键,属于基础题.
3.A
【解析】
设提价后价格是元(),求出销售量得总收入,列不等式求解.
【详解】
设提价后价格是元(),则销售量为(万本)
销售总收入为,
由,得,∴
∴提价后至多为每本4元.
故选:A.
【点睛】
关键点点睛:本题考查函数的应用,解题时需引入参数,可根据已知函数模型列出函数或不等式求解.本题要注意的单位要统一,销售收入是以元为单位还是以万元为单位要一致,否则易出错.
4.B
【解析】
【分析】
根据表格中可知函数的单调性,可选择合适的函数模型,然后令,解方程即可得解.
【详解】
由表格中的数据可知,函数单调递增,故合适的函数模型为,
令,解得.
故选:B.
5.B
【解析】
【分析】
根据题意原函数是一个周期函数,以2018为周期的函数,根据二次函数的对称性得到结果即可.
【详解】
根据题意原函数是一个周期函数,以2018为周期的函数,,
根据二次函数的图形的特点得到,最大值在x=0或者x=2018处取得,f(0)=1,对称轴为,故只需要.
故答案为B.
【点睛】
本题考查了函数的周期性和二次函数的图像的性质和最值问题,二次函数的最值和轴与区间的位置关系是有联系的.
6.D
【解析】
【分析】
利用题中的条件先计算出的值,再代入数据即可得出结果.
【详解】
由题意知:
,
,
即,
等式两边同时取对数得,
,
则;
设温度为的水冷却到所经过的时间为,
则,
即,
解得;
故选:D.
7.D
【解析】
【分析】
根据一次函数的图象与性质,分类讨论列出方程,即可求解.
【详解】
当时,函数,显然不符合题意;
当时,函数为单调递减函数,所以,解得;
当时,函数为单调递增函数,所以,解得.
综上可得,实数的值为或.
故选:D.
8.A
【解析】
【分析】
根据三个事件的特征,分析离家距离的变化情况,选出符合事件的图像.
【详解】
对于事件①,中途返回家,离家距离为0,故图像④符合;
对于事件②,堵车中途耽搁了一些时间,中间有段时间离家距离不变,故图像①符合;
对于事件③,前面速度慢,后面赶时间加快速度,故图像②符合;
故选:A.
9.C
【解析】
【详解】
设AB=a,则y=a2 x2= x2+a2,
其图象为抛物线的一段,开口向下,顶点在y轴上方,
本题选择C选项.
10.C
【解析】
【分析】
因为该汽艇沿直线方向匀速开往改岛,靠近岛时,绕小岛环行两周后,把汽艇停靠岸边考查,然后又乘汽艇沿原航线提速返回,由此即可求出答案.
【详解】
解:因为该汽艇中途停靠岸边考察,此时间段不变,绕小岛环行两周,汽艇与码头的距离最小值,不会低于靠近海岛时的距离,故排除,,
因为为汽艇与码头在时刻的距离,其图象能表示的函数关系,而图表示的不是函数关系,故排除.
故选:.
【点睛】
本题函数图象的应用,同学们要注意分析其中得“关键点”,还要善于分析各图象的变化趋势,属于基础题.
11.C
【解析】
为求矩形面积的最大值,可先将其面积表达出来,又要注意点在长方形内,所以要注意分析自变量的取值范围,并以自变量的限制条件为分类标准进行分类讨论.
【详解】
解:设长为,则长为
又因为要将点围在矩形内,
则矩形的面积为,
当时,当且仅当时,
当时,
分段画出函数图形可得其形状与接近
故选:.
【点睛】
解决本题的关键是将的表达式求出来,结合自变量的取值范围,分类讨论后求出的解析式,属于基础题.
12.D
【解析】
【分析】
将函数的解析式表示为分段函数,进而可判断出函数的图象.
【详解】
,则,
因此,函数的图象如D选项中的图象所示.
故选:D.
【点睛】
本题考查指数型函数图象的识别,化简函数解析式是判断的关键,属于基础题.
13.A
【解析】
【分析】
根据题意,结合图形,分析区间(0,)和(,π)上f(x)的符号,再分析f(x)的对称性,排除BCD,即可得答案.
【详解】
根据题意,f(x)=|PB|2﹣|PA|2,∠ADP=x.
在区间(0,)上,P在边AC上,|PB|>|PA|,则f(x)>0,排除C;
在区间(,π)上,P在边BC上,|PB|<|PA|,则f(x)<0,排除B,
又由当x1+x2=π时,有f(x1)=﹣f(x2),f(x)的图象关于点(,0)对称,排除D,
故选:A
14.A
【解析】
【分析】
先求得利润的表达式,然后结合二次函数的性质求得利润取得最大值时对应的生产数量.
【详解】
利润
.
所以当时,L(x)有最大值.
故选:A
【点睛】
本小题主要考查二次函数模型的应用,属于基础题.
15.ABC
【解析】
【分析】
通过图象判断选项ABC正确;第一次服用该药物1单位3小时后与第2次服用该药物1单位1小时后,一定会发生药物中毒,故选项D错误.
【详解】
从图象中可以看出,首次服用该药物1单位约10分钟后药物发挥治疗作用,故选项A正确;
根据图象可知,首次服用该药物1单位约1小时后的血药浓度达到最大值,由图象可知两次服药间隔小于2小时,一定会产生药物中毒,故选项B正确;
服药5.5小时时,血药浓度等于最低有效浓度,此时再服药,血药浓度增加,可使药物持续发挥治疗作用,故选项C正确;
第一次服用该药物1单位3小时后与第2次服用该药物1单位1小时后,血药浓度之和大于最低中毒浓度,因此一定会发生药物中毒,故选项D错误.
故选:ABC.
16.ABC
【解析】
【分析】
利用待定系数法求出函数解析式,并根据函数解析式计算药含量变化情况得答案.
【详解】
解:当时,设,则,故,则,故正确;
当时,把代入,可得,则,即,故正确;
当时,,故正确;
当时,由,得,当时,由,得,即,
分钟,故错误.
故选:.
17.
【解析】
【分析】
先将D=a-A进行配方,求出D取最大值时的A的值,即可得出结论.
【详解】
由题意得,D=a-A=-(-+,且A≥0,∴当=,即A=时,D最大,故答案为.
【点睛】
本题考查了二次函数最值的求法,关键是对解析式进行配方即得函数的最值以及对应的自变量的值.
18.11.1
【解析】
【分析】
将出租车行驶了11.5km,分为三部分计费:出租车行驶3km,需要6元,3km到10km,需要元,再行驶1.5km,需要元,从而可得结果.
【详解】
根据题意,行驶10km时,付车费,再行驶1.5km,增加车费1.6元,则应付车费元,
故答案为:11.1
【点睛】
此题考查分段函数的应用,考查分析问题的能力,属于基础题.
19.10
【解析】
【分析】
建立面积的函数关系式,利用二次函数求出取最大值时的x.
【详解】
设每个花圃的面积的面积为y,则
因为,
所以当时,y最大.
故答案为:10.
【点睛】
数学建模是高中数学六大核心素养之一,在高中数学中,应用题是常见考查形式:
(1)求解应用性问题时,首先要弄清题意,分清条件和结论,抓住关键词和量,理顺数量关系,然后将文字语言转化成数学语言,建立相应的数学模型;
(2)求解应用性问题时,不仅要考虑函数本身的定义域,还要结合实际问题理解自变量的取值范围.
20.(1);(2).
【解析】
(1)代入求值即可;
(2)对进行讨论,令解出即可.
【详解】
解:函数,
,
,
;
,
当时,,
解得:,不成立;
当时,,
解得:,成立;
当时,,
此方程无解,
综上所述:实数a的值为.
21.当时,汽车总费用最小;当时,火车总费用最小;当时,飞机总费用最小(其中表示运输路程)
【解析】
【分析】
根据路程分别求出三种运输工具的费用与损耗之和(即途中费用+装卸费用+运输损耗),然后比较可得.
【详解】
设路程为,汽车、火车、飞机三种运输工具的费用与损耗之和分别为,则
,
,
,
从三条直线的斜率和纵截距,它们的图象大致位置如图所示,
时,,时,,
所以当时,最小,汽车总费用最小,当时,最小,火车总费用最小,当时,最小,飞机总费用最小.
答:当时,汽车总费用最小;当时,火车总费用最小;当时,飞机总费用最小(其中表示运输路程)
【点睛】
本题考查函数模型的应用,解题关键求出三个函数式,然后比较它们的大小.
22.元;第25天
【解析】
【分析】
分情况讨论即可获得日销售金额y关于时间t的函数关系式,根据分段函数不同段上的表达式,分别求最大值取较大者即可解答.
【详解】
∵日销售金额,
∴
.
当,,时,(元);
当,,时.(元);
∵,∴第25天日销售金额最大,(元).
【点睛】
本题考查分段函数的应用,考查分类讨论的思想、二次函数求最值得方法以及问题转化的能力,属于中档题.
23.当猪圈正面底边为4米侧面底边为3米时, 总造价最低为4000元.
【解析】
【详解】
试题分析:解:设猪圈底面正面的边长为xm,则其侧面边长为m---(2分)那么猪圈的总造价y=3x×120+3××80×2+112=360x++1120,---(3分)因为360x+≥2 =2880,---(2分)当且仅当360x=,即x=4时取“=”,(1分)所以当猪圈正面底边为4米侧面底边为3米时,总造价最低为4000元
考点:基本不等式在最值问题中的应用
点评:本小题主要考基本不等式在最值问题中的应用等基础知识,观察函数特点:为一个含有两个部分,这两部分的积为一个常数,求和的最值,所以利用基本不等式求最值.
24.(1);(2).
【解析】
【分析】
(1)当时,可得,利用二次函数的基本性质可求得函数的值域;
(2)分析可知,对于任意的实数,恒成立,对实数的取值进行分类讨论,可得出关于实数的不等式组,由此可求得实数的取值范围.
【详解】
(1)当时,,
因为,故,所以函数的值域为;
(2)由题意恒成立,
恒成立,
所以,只要恒成立即可,即恒成立.
①当时,恒成立,符合题意;
②当时,则有,解得.
综上所述:.
25.(1)[2,] (2)-<a<(3)(-,-)∪(,)
【解析】
【分析】
(1)当a=1时,f(x)=x+,结合对勾函数的图象和性质,可得f(x)在[,2]上的值域;
(2)若不等式f(2x)<2x++4在[0,1]上恒成立,即a<-2(2x)2+1+2x在[0,1]上恒成立,令t=2x,则t∈[1,2],y=-2t2+t+1,结合二次函数的图象和性质,求出函数的最小值,可得实数a的取值范围;
(3)换元,原问题等价于求实数a的范围,使得函数在给定的区间上,恒有2ymin>ymax
【详解】
解:(1)函数,
当a=1时,f(x)=x+,导数为f′(x)=1-=,
f(x)在[,1]上为减函数,在[1,2]上为增函数,
∴当x=,或x=2时,函数最最大值,当x=1时,函数取最小值2,
故f(x)在[,2]上的值域为[2,];
(2)若不等式f(2x)<2x++4在[0,1]上恒成立,
即2x+<2x++4在[0,1]上恒成立,即a2<1+4 2x在[0,1]上恒成立,
1+4 2x在[0,1]递增,可得最小值为1+4=5,即a2<5,解得-<a<;
(3)设t=g(x)==-1+在x∈[0,]递减,可得t∈[,1],则y=t+,
原问题转化为求实数a的取值范围,使得y在区间[,1]上,恒有2ymin>ymax.
讨论:①当0<a2≤时,y=t+在[,1]上递增,∴ymin=3a2+,ymax=a2+1,
由2ymin>ymax得a2>,∴<a≤;或-≤a<-;
②当<a2≤时,y=t+在[,|a|]上单调递减,在[|a|,1]上单调递增,
∴ymin=2|a|,ymax=max{3a2+,a2+1}=a2+1,
由2ymin>ymax得2-<|a|<2+,∴<|a|≤;
③当<|a|<1时,y=t+在[,|a|]上单调递减,在[|a|,1]上单调递增,
∴ymin=2|a|,ymax=max{3a2+,a2+1}=3a2+,
由2ymin>ymax得<|a|<,∴<|a|<1;
④当|a|≥1时,y=t+在[,1]上单调递减,∴ymin=a2+1,ymax=3a2+,
由2ymin>ymax得a2<,∴1≤a2<;
综上,a的取值范围是(-,-)∪(,).
【点睛】
本题主要考查了函数的基本性质的应用问题,其中解答中熟练应用函数的单调性与函数的奇偶性,合理分类讨论求解函数的最值是解答的关键,着重考查了分类讨论思想和转化思想的应用,以及分析问题和解答问题的能力,属于中档试题.
26.(1);(2).
【解析】
【分析】
(1)把代入即可求得的值;
(2)根据,通过分段讨论列出不等式组,从而求解.
【详解】
(1)由题意可知,故;
(2)因为,所以,
又因为时,药物释放量对人体有害,
所以或,解得或,所以,
由,故对人体有害的时间为.
27.(1);(2)该产品的年产量为台时,公司所获利润最大,最大利润是万元.
【解析】
【分析】
(1)根据年利润等于总收入减去固定成本万再减去另投入成本,写成分段函数的形式即可;
(2)分别由二次函数的性质以及基本不等式求出分段函数各段的最大值,再比较取最大值即可求解.
【详解】
(1)由题意可得:
当时,
;
当时,,
所以
(2)若,,
所以当时,万元.
若,,
当且仅当时,即时,万元.
所以该产品的年产量为台时,公司所获利润最大,最大利润是万元.
试卷第页,共页
试卷第页,共页
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
