北师大版七年级下册1.6 完全平方公式 同步练习(word版含答案)
文档属性
| 名称 | 北师大版七年级下册1.6 完全平方公式 同步练习(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 130.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-18 19:15:35 | ||
图片预览


文档简介
1.6 完全平方公式
一、选择题(共10小题;共50分)
1. 若 是完全平方式,则 的值是
A. B. C. D.
2. 张长为 、宽为 的长方形纸片按如图所示的方式拼成一个边长为 的正方形,图中空白部分的面积为 ,阴影部分的面积为 .若 ,则 , 满足
A. B. C. D.
3. 某人将 看成了一个填数游戏式:.于是,他在每个框中各填写了一个两位数 与 ,结果发现,所得到的六位数 恰是一个完全立方数.则
A. B. C. D.
4. 已知 ,则 的值为
A. B. C. D.
5. 用大小相等的小正方形按一定规律拼成下列图形,则第 个图形中小正方形的个数是
A. B. C. D.
6. 利用完全平方公式计算 得
A. B. C. D.
7. 已知 ,则 的值为
A. B. C. D.
8. 已知 ,,则 的值为
A. B. C. D.
9. 若 ,,则 的值是
A. B. C. D.
10. 我国宋朝数学家杨辉 年的著作《详解九章算法》给出了在 ( 为非负整数)的展开式中,把各项系数按一定的规律排成右表(展开后每一项按 的次数由大到小的顺序排列).人们把这个表叫做“杨辉三角”.据此规律,则 展开式中含 项的系数是
A. B. C. D.
二、填空题(共5小题;共25分)
11. 如果 是一个完全平方式,那么 的值为 .
12. 已知 ,,,且 ,则 的值等于 .
13. 计算: .
14. 如图是我国数学家发明的“杨辉三角”,此图揭示了 ( 为非负整数)的展开式的项数及其系数的有关规律.请你观察,并根据此规律写出 的展开式共有 项,第二项的系数是 , 的展开式共有 项,各项的系数和是 .
15. 将代数式 配方后,发现它的最小值为 .
三、解答题(共4小题;共52分)
16. 利用完全平方公式计算:
(1);
(2);
(3);
(4).
17. 化简并求值:,其中 .
18. 已知 ,,求下列各式的值.
(1);
(2).
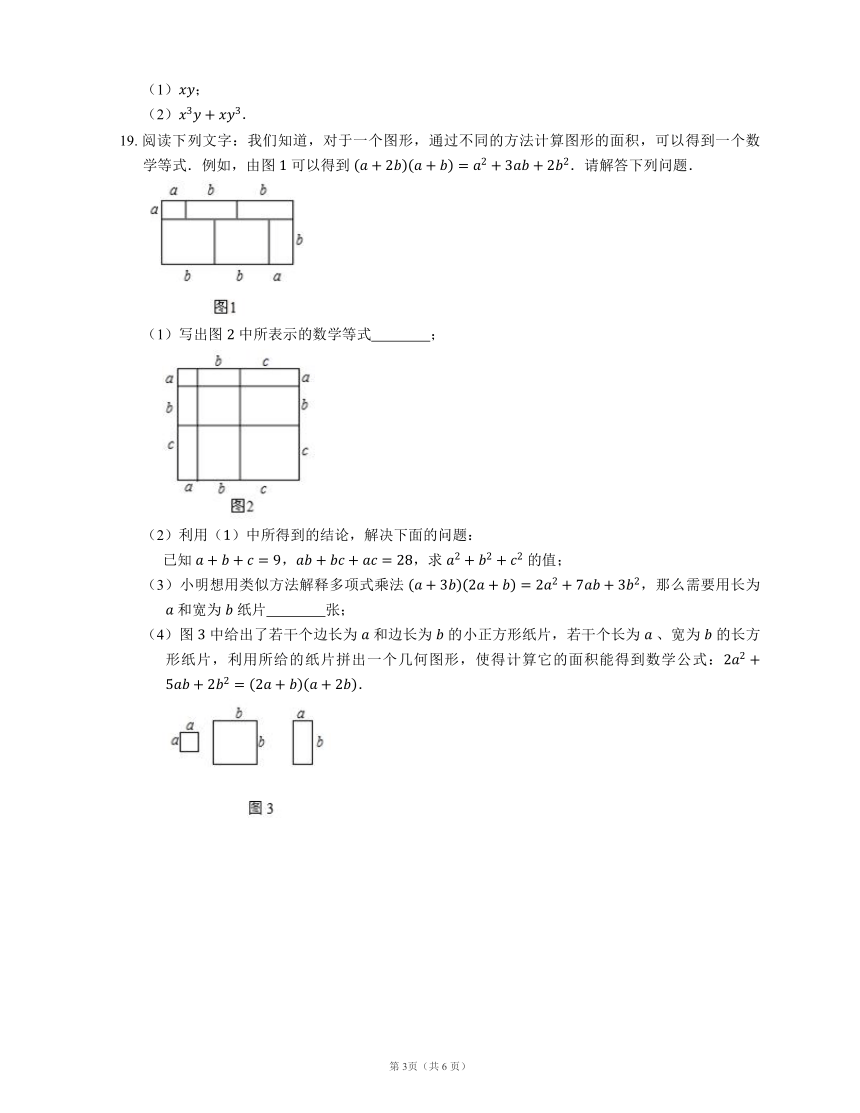
19. 阅读下列文字:我们知道,对于一个图形,通过不同的方法计算图形的面积,可以得到一个数学等式.例如,由图 可以得到 .请解答下列问题.
(1)写出图 中所表示的数学等式 ;
(2)利用()中所得到的结论,解决下面的问题:
已知 ,,求 的值;
(3)小明想用类似方法解释多项式乘法 ,那么需要用长为 和宽为 纸片 张;
(4)图 中给出了若干个边长为 和边长为 的小正方形纸片,若干个长为 、宽为 的长方形纸片,利用所给的纸片拼出一个几何图形,使得计算它的面积能得到数学公式:.
答案
第一部分
1. D
2. D 【解析】由题图可知 ,
,
,
,
整理得 ,
,
.
故选D.
3. D
4. B 【解析】因为 ,
所以 ,,
所以 ,,
故选B.
5. C
6. D 【解析】
7. D 【解析】,
,
,
,
.
8. C 【解析】,
,
,
.
9. C 【解析】因为 ,所以
因为 ,所以 ,所以
① ②,得 ,所以 .
10. D
【解析】由题意,,
可知,展开式中第二项为 ,
所以 展开式中含 项的系数是 .
第二部分
11.
12.
【解析】,,,
,,,
.
13.
14. ,,,
【解析】 的展开式有 项; 的展开式有 项; 的展开式有 项; 故 的展开式共有 项.由题中规律得 的展开式中第二项的系数为 , 的展开式中第二项的系数为 ,故 的展开式中第二项的系数为 .
的展开式中各项的系数和为 ;
的展开式中各项的系数和为 ;
的展开式中各项的系数和为 ;
故 的展开式中各项的系数和为 .
15.
【解析】,当 时,代数式有最小值,最小值为 .
第三部分
16. (1)
(2)
(3)
(4)
17.
当 时,
.
18. (1)
由① ②,得 .
所以 .
(2) 由① ②,得 .
所以 .
所以 .
19. (1)
(2)
(3)
(4)
第1页(共1 页)
一、选择题(共10小题;共50分)
1. 若 是完全平方式,则 的值是
A. B. C. D.
2. 张长为 、宽为 的长方形纸片按如图所示的方式拼成一个边长为 的正方形,图中空白部分的面积为 ,阴影部分的面积为 .若 ,则 , 满足
A. B. C. D.
3. 某人将 看成了一个填数游戏式:.于是,他在每个框中各填写了一个两位数 与 ,结果发现,所得到的六位数 恰是一个完全立方数.则
A. B. C. D.
4. 已知 ,则 的值为
A. B. C. D.
5. 用大小相等的小正方形按一定规律拼成下列图形,则第 个图形中小正方形的个数是
A. B. C. D.
6. 利用完全平方公式计算 得
A. B. C. D.
7. 已知 ,则 的值为
A. B. C. D.
8. 已知 ,,则 的值为
A. B. C. D.
9. 若 ,,则 的值是
A. B. C. D.
10. 我国宋朝数学家杨辉 年的著作《详解九章算法》给出了在 ( 为非负整数)的展开式中,把各项系数按一定的规律排成右表(展开后每一项按 的次数由大到小的顺序排列).人们把这个表叫做“杨辉三角”.据此规律,则 展开式中含 项的系数是
A. B. C. D.
二、填空题(共5小题;共25分)
11. 如果 是一个完全平方式,那么 的值为 .
12. 已知 ,,,且 ,则 的值等于 .
13. 计算: .
14. 如图是我国数学家发明的“杨辉三角”,此图揭示了 ( 为非负整数)的展开式的项数及其系数的有关规律.请你观察,并根据此规律写出 的展开式共有 项,第二项的系数是 , 的展开式共有 项,各项的系数和是 .
15. 将代数式 配方后,发现它的最小值为 .
三、解答题(共4小题;共52分)
16. 利用完全平方公式计算:
(1);
(2);
(3);
(4).
17. 化简并求值:,其中 .
18. 已知 ,,求下列各式的值.
(1);
(2).
19. 阅读下列文字:我们知道,对于一个图形,通过不同的方法计算图形的面积,可以得到一个数学等式.例如,由图 可以得到 .请解答下列问题.
(1)写出图 中所表示的数学等式 ;
(2)利用()中所得到的结论,解决下面的问题:
已知 ,,求 的值;
(3)小明想用类似方法解释多项式乘法 ,那么需要用长为 和宽为 纸片 张;
(4)图 中给出了若干个边长为 和边长为 的小正方形纸片,若干个长为 、宽为 的长方形纸片,利用所给的纸片拼出一个几何图形,使得计算它的面积能得到数学公式:.
答案
第一部分
1. D
2. D 【解析】由题图可知 ,
,
,
,
整理得 ,
,
.
故选D.
3. D
4. B 【解析】因为 ,
所以 ,,
所以 ,,
故选B.
5. C
6. D 【解析】
7. D 【解析】,
,
,
,
.
8. C 【解析】,
,
,
.
9. C 【解析】因为 ,所以
因为 ,所以 ,所以
① ②,得 ,所以 .
10. D
【解析】由题意,,
可知,展开式中第二项为 ,
所以 展开式中含 项的系数是 .
第二部分
11.
12.
【解析】,,,
,,,
.
13.
14. ,,,
【解析】 的展开式有 项; 的展开式有 项; 的展开式有 项; 故 的展开式共有 项.由题中规律得 的展开式中第二项的系数为 , 的展开式中第二项的系数为 ,故 的展开式中第二项的系数为 .
的展开式中各项的系数和为 ;
的展开式中各项的系数和为 ;
的展开式中各项的系数和为 ;
故 的展开式中各项的系数和为 .
15.
【解析】,当 时,代数式有最小值,最小值为 .
第三部分
16. (1)
(2)
(3)
(4)
17.
当 时,
.
18. (1)
由① ②,得 .
所以 .
(2) 由① ②,得 .
所以 .
所以 .
19. (1)
(2)
(3)
(4)
第1页(共1 页)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
