北师大版七年级下册 第四章 三角形 章节测试(word版含答案)
文档属性
| 名称 | 北师大版七年级下册 第四章 三角形 章节测试(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 947.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-18 21:07:50 | ||
图片预览

文档简介
三角形 章节测试
一、选择题(共10小题;共50分)
1. 一块三角形玻璃样板不慎被小强同学碰破,成了四片完整四碎片(如图所示),聪明的小强经过仔细的考虑认为只要带其中的两块碎片去玻璃店就可以让师傅画一块与以前一样的玻璃样板.你认为下列四个答案中正确的是
A. 带其中的任意两块去都可以 B. 带 , 去就可以了
C. 带 , 或 , 去就可以了 D. 带 , 去就可以了
2. 如图,三边均不等长的锐角 ,若在此三角形内找一点 ,使得 ,, 的面积均相等.下列作法中正确的是
A. 作中线 ,再取 的中点
B. 分别作 , 的高线,再取此两高线的交点
C. 分别作中线 ,,再取此两中线的交点
D. 分别作 , 的角平分线,再取此两角平分线的交点
3. 如图,,,且 交 于点 ,在原图形的基础上,要利用“”证明 ,可以添加的条件是
A. B. C. D.
4. 在 中,,以 的一边为边画等腰三角形,使得它的第三个顶点在 的其他边上,则可以画出的不同的等腰三角形的个数最多可画几个
A. 个 B. 个 C. 个 D. 个
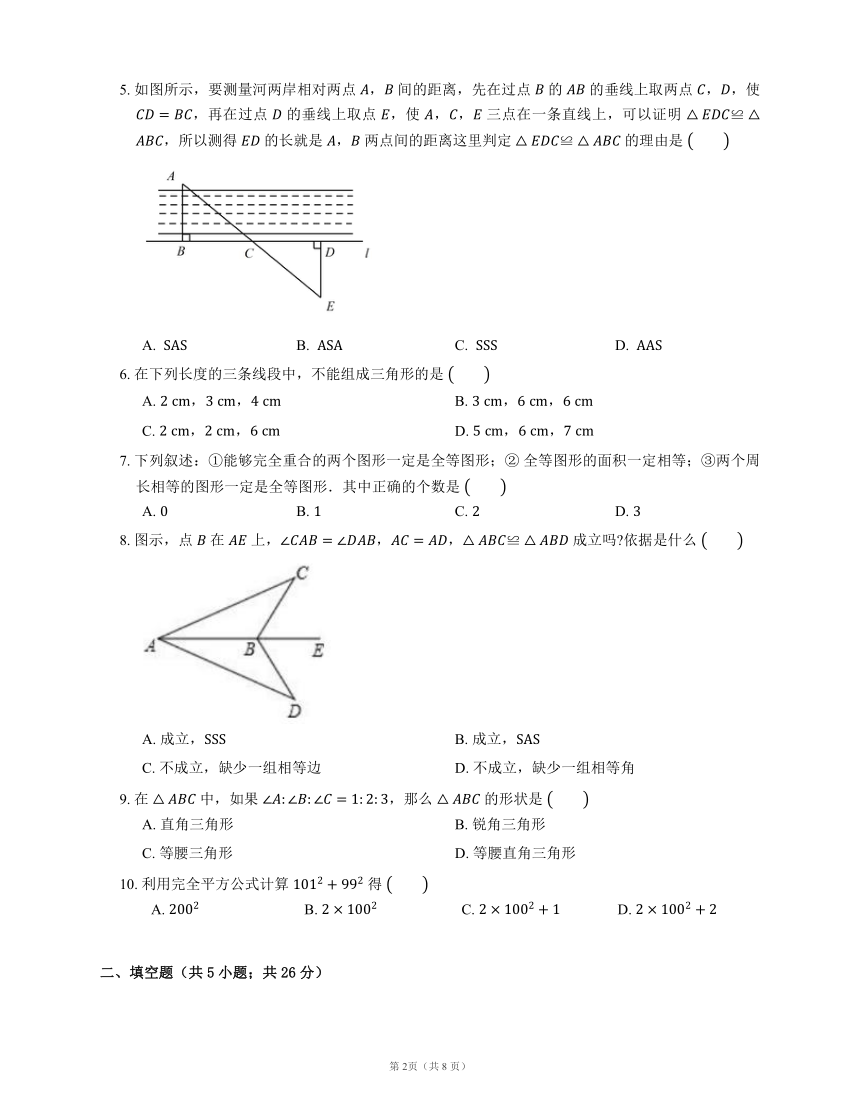
5. 如图所示,要测量河两岸相对两点 , 间的距离,先在过点 的 的垂线上取两点 ,,使 ,再在过点 的垂线上取点 ,使 ,, 三点在一条直线上,可以证明 ,所以测得 的长就是 , 两点间的距离这里判定 的理由是
A. B. C. D.
6. 在下列长度的三条线段中,不能组成三角形的是
A. ,, B. ,,
C. ,, D. ,,
7. 下列叙述:①能够完全重合的两个图形一定是全等图形;② 全等图形的面积一定相等;③两个周长相等的图形一定是全等图形.其中正确的个数是
A. B. C. D.
8. 图示,点 在 上,,, 成立吗 依据是什么
A. 成立, B. 成立,
C. 不成立,缺少一组相等边 D. 不成立,缺少一组相等角
9. 在 中,如果 ,那么 的形状是
A. 直角三角形 B. 锐角三角形
C. 等腰三角形 D. 等腰直角三角形
10. 利用完全平方公式计算 得
A. B. C. D.
二、填空题(共5小题;共26分)
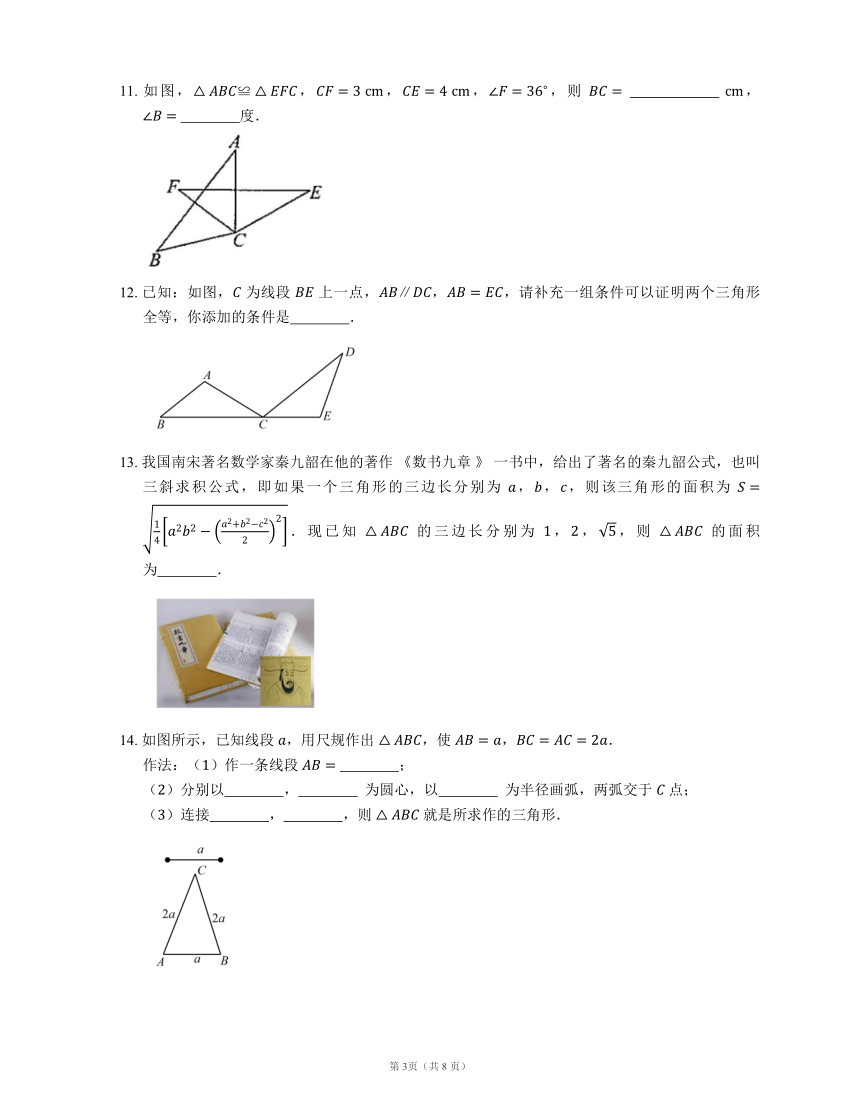
11. 如图,,,,,则 , 度.
12. 已知:如图, 为线段 上一点,,,请补充一组条件可以证明两个三角形全等,你添加的条件是 .
13. 我国南宋著名数学家秦九韶在他的著作 《数书九章 》 一书中,给出了著名的秦九韶公式,也叫三斜求积公式,即如果一个三角形的三边长分别为 ,,,则该三角形的面积为 .现已知 的三边长分别为 ,,,则 的面积为 .
14. 如图所示,已知线段 ,用尺规作出 ,使 ,.
作法:()作一条线段 ;
()分别以 , 为圆心,以 为半径画弧,两弧交于 点;
()连接 , ,则 就是所求作的三角形.
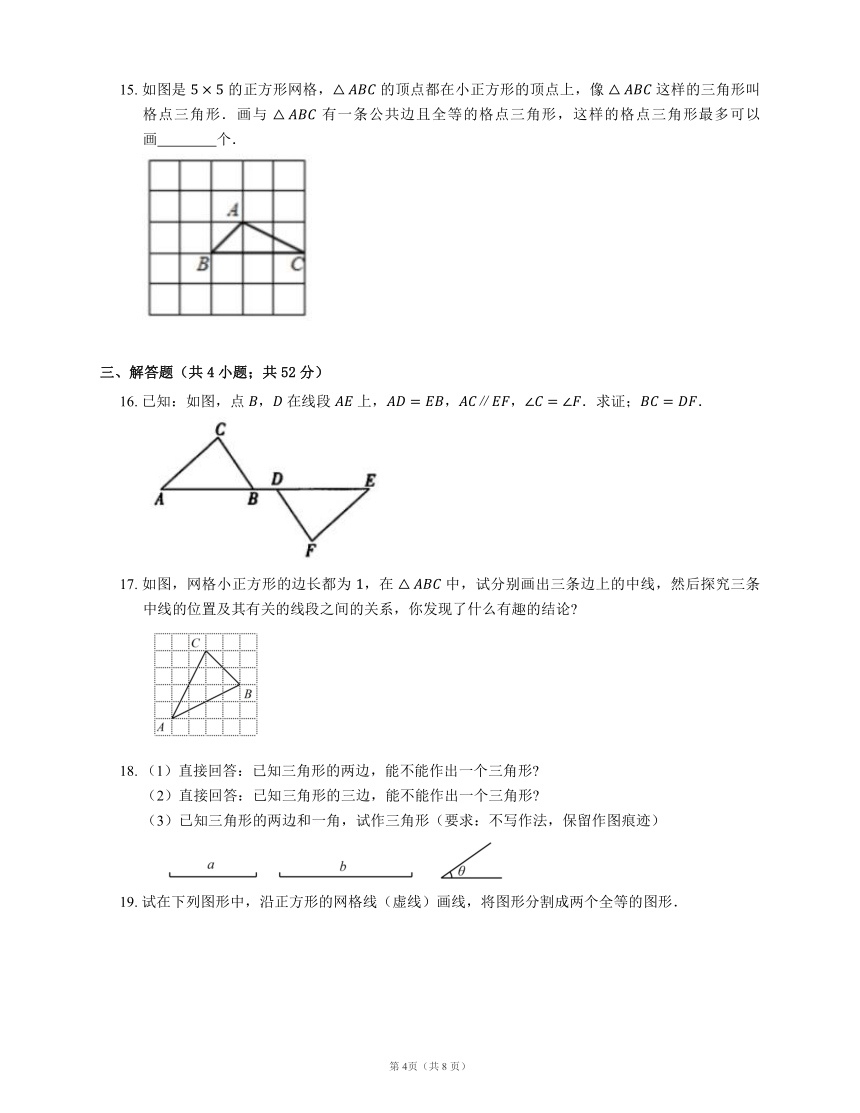
15. 如图是 的正方形网格, 的顶点都在小正方形的顶点上,像 这样的三角形叫格点三角形.画与 有一条公共边且全等的格点三角形,这样的格点三角形最多可以画 个.
三、解答题(共4小题;共52分)
16. 已知:如图,点 , 在线段 上,,,.求证;.
17. 如图,网格小正方形的边长都为 ,在 中,试分别画出三条边上的中线,然后探究三条中线的位置及其有关的线段之间的关系,你发现了什么有趣的结论
18. (1)直接回答:已知三角形的两边,能不能作出一个三角形
(2)直接回答:已知三角形的三边,能不能作出一个三角形
(3)已知三角形的两边和一角,试作三角形(要求:不写作法,保留作图痕迹)
19. 试在下列图形中,沿正方形的网格线(虚线)画线,将图形分割成两个全等的图形.
答案
第一部分
1. C 【解析】带③,④可以用“角边角”确定三角形,
带①,④可以用“角边角”确定三角形,
带②④可以延长还原出原三角形.
2. C
3. A
4. B 【解析】如图:
5. B
6. C 【解析】选项A.,能组成三角形;
选项B.,能组成三角形;
选项C.,不能组成三角形;
选项D.,能够组成三角形.
故选C.
7. C 【解析】①②正确.
8. B 【解析】在 和 中,
, 故答案为:B.
9. A
10. D
【解析】
第二部分
11. ,
12. (答案不唯一)
13.
14. ,,,,,
15.
【解析】如图,
以 为公共边可画出 ,, 三个三角形和原三角形全等.
以 为公共边可画出三个三角形 ,, 和原三角形全等.
所以可画出 个.
第三部分
16. ,
即 .
,
.
在 和 中,
,
.
17. 所画中线如图所示.
发现的结论:①三条中线交于一点;②在同一条中线上,中线的交点与边中点所连线段的长度等于它与顶点所连线段的长度的一半.
18. (1) 不能
(2) 能
(3) 答案不唯一
19. 如图所示(第一个图形画法不唯一).
第1页(共1 页)
一、选择题(共10小题;共50分)
1. 一块三角形玻璃样板不慎被小强同学碰破,成了四片完整四碎片(如图所示),聪明的小强经过仔细的考虑认为只要带其中的两块碎片去玻璃店就可以让师傅画一块与以前一样的玻璃样板.你认为下列四个答案中正确的是
A. 带其中的任意两块去都可以 B. 带 , 去就可以了
C. 带 , 或 , 去就可以了 D. 带 , 去就可以了
2. 如图,三边均不等长的锐角 ,若在此三角形内找一点 ,使得 ,, 的面积均相等.下列作法中正确的是
A. 作中线 ,再取 的中点
B. 分别作 , 的高线,再取此两高线的交点
C. 分别作中线 ,,再取此两中线的交点
D. 分别作 , 的角平分线,再取此两角平分线的交点
3. 如图,,,且 交 于点 ,在原图形的基础上,要利用“”证明 ,可以添加的条件是
A. B. C. D.
4. 在 中,,以 的一边为边画等腰三角形,使得它的第三个顶点在 的其他边上,则可以画出的不同的等腰三角形的个数最多可画几个
A. 个 B. 个 C. 个 D. 个
5. 如图所示,要测量河两岸相对两点 , 间的距离,先在过点 的 的垂线上取两点 ,,使 ,再在过点 的垂线上取点 ,使 ,, 三点在一条直线上,可以证明 ,所以测得 的长就是 , 两点间的距离这里判定 的理由是
A. B. C. D.
6. 在下列长度的三条线段中,不能组成三角形的是
A. ,, B. ,,
C. ,, D. ,,
7. 下列叙述:①能够完全重合的两个图形一定是全等图形;② 全等图形的面积一定相等;③两个周长相等的图形一定是全等图形.其中正确的个数是
A. B. C. D.
8. 图示,点 在 上,,, 成立吗 依据是什么
A. 成立, B. 成立,
C. 不成立,缺少一组相等边 D. 不成立,缺少一组相等角
9. 在 中,如果 ,那么 的形状是
A. 直角三角形 B. 锐角三角形
C. 等腰三角形 D. 等腰直角三角形
10. 利用完全平方公式计算 得
A. B. C. D.
二、填空题(共5小题;共26分)
11. 如图,,,,,则 , 度.
12. 已知:如图, 为线段 上一点,,,请补充一组条件可以证明两个三角形全等,你添加的条件是 .
13. 我国南宋著名数学家秦九韶在他的著作 《数书九章 》 一书中,给出了著名的秦九韶公式,也叫三斜求积公式,即如果一个三角形的三边长分别为 ,,,则该三角形的面积为 .现已知 的三边长分别为 ,,,则 的面积为 .
14. 如图所示,已知线段 ,用尺规作出 ,使 ,.
作法:()作一条线段 ;
()分别以 , 为圆心,以 为半径画弧,两弧交于 点;
()连接 , ,则 就是所求作的三角形.
15. 如图是 的正方形网格, 的顶点都在小正方形的顶点上,像 这样的三角形叫格点三角形.画与 有一条公共边且全等的格点三角形,这样的格点三角形最多可以画 个.
三、解答题(共4小题;共52分)
16. 已知:如图,点 , 在线段 上,,,.求证;.
17. 如图,网格小正方形的边长都为 ,在 中,试分别画出三条边上的中线,然后探究三条中线的位置及其有关的线段之间的关系,你发现了什么有趣的结论
18. (1)直接回答:已知三角形的两边,能不能作出一个三角形
(2)直接回答:已知三角形的三边,能不能作出一个三角形
(3)已知三角形的两边和一角,试作三角形(要求:不写作法,保留作图痕迹)
19. 试在下列图形中,沿正方形的网格线(虚线)画线,将图形分割成两个全等的图形.
答案
第一部分
1. C 【解析】带③,④可以用“角边角”确定三角形,
带①,④可以用“角边角”确定三角形,
带②④可以延长还原出原三角形.
2. C
3. A
4. B 【解析】如图:
5. B
6. C 【解析】选项A.,能组成三角形;
选项B.,能组成三角形;
选项C.,不能组成三角形;
选项D.,能够组成三角形.
故选C.
7. C 【解析】①②正确.
8. B 【解析】在 和 中,
, 故答案为:B.
9. A
10. D
【解析】
第二部分
11. ,
12. (答案不唯一)
13.
14. ,,,,,
15.
【解析】如图,
以 为公共边可画出 ,, 三个三角形和原三角形全等.
以 为公共边可画出三个三角形 ,, 和原三角形全等.
所以可画出 个.
第三部分
16. ,
即 .
,
.
在 和 中,
,
.
17. 所画中线如图所示.
发现的结论:①三条中线交于一点;②在同一条中线上,中线的交点与边中点所连线段的长度等于它与顶点所连线段的长度的一半.
18. (1) 不能
(2) 能
(3) 答案不唯一
19. 如图所示(第一个图形画法不唯一).
第1页(共1 页)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
