北京市门头沟区2021-2022学年高三上学期期末调研数学试题(Word版含答案)
文档属性
| 名称 | 北京市门头沟区2021-2022学年高三上学期期末调研数学试题(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 999.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-18 00:00:00 | ||
图片预览




文档简介
门头沟区2021-2022学年度第一学期期末调研
高 三 数学 2022.1
考 生 须 知 1.本试卷共6页,共3道大题,21个小题。满分100分。考试时间90分钟。 2.在试卷和答题卡上准确填写学校和姓名,并将考试编号填写(或条形码粘贴)在答题卡相应位置处。 3.试题答案一律填涂或书写在答题卡上,在试卷上作答无效。选择题、作图题用2B铅笔作答,其它试题用黑色字迹签字笔作答。 4.考试结束,将试卷、答题卡和草稿纸一并交回。
第一部分(选择题 共40分)
一、选择题(本大题共10个小题,每小题4分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。)
(1)复数
(A) (B)
(C) (D)
(2)集合,,则
(A) (B)
(C) (D)
(3)在的展开式中,的系数是
(A) (B)
(C) (D)
(4) “角的终边关于轴对称”是“”的
(A)充分不必要条件 (B)必要不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
(5)下列函数中,在为增函数的是
(A) (B)
(C) (D)
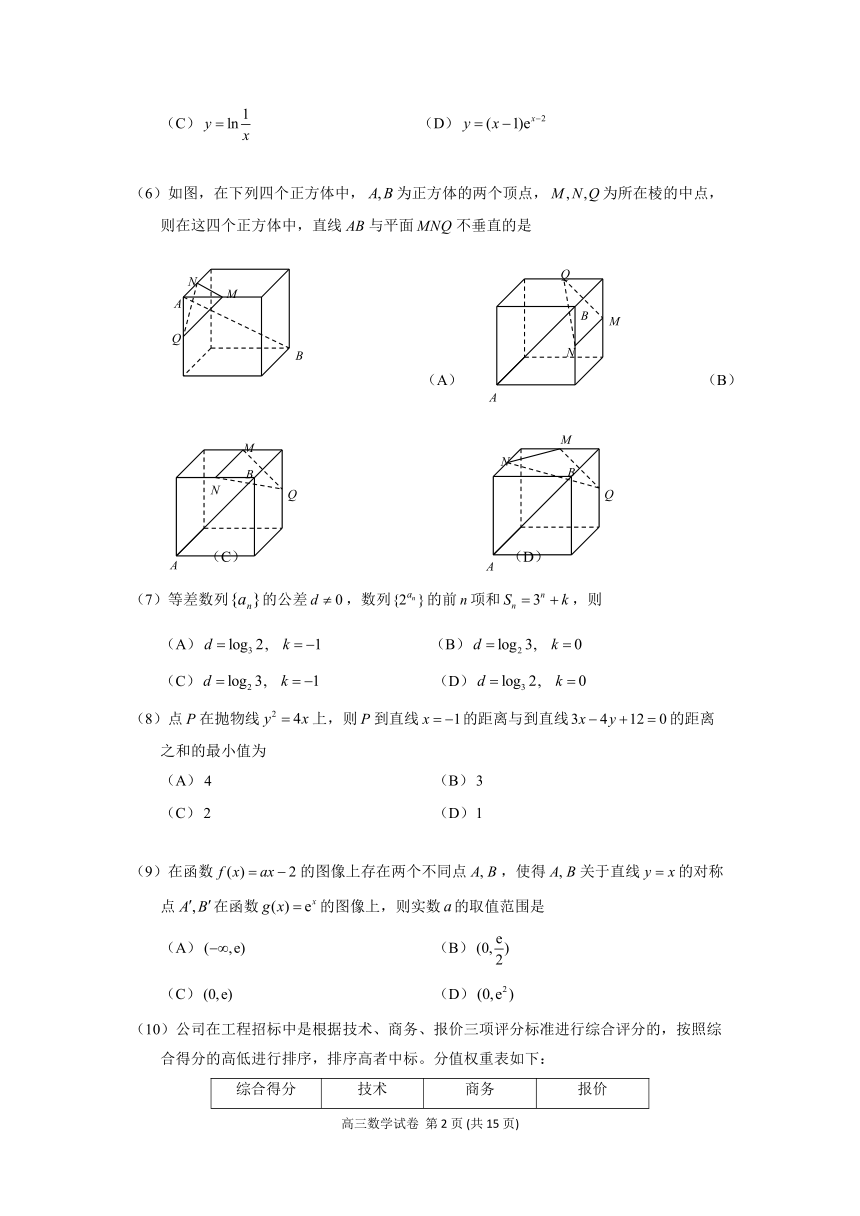
(6)如图,在下列四个正方体中,为正方体的两个顶点,为所在棱的中点,则在这四个正方体中,直线与平面不垂直的是
(A) (B)
(C) (D)
(7)等差数列的公差,数列的前项和,则
(A) (B)
(C) (D)
(8)点在抛物线上,则到直线的距离与到直线的距离之和的最小值为
(A) (B)
(C) (D)
(9)在函数的图像上存在两个不同点,使得关于直线的对称点在函数的图像上,则实数的取值范围是
(A) (B)
(C) (D)
(10)公司在工程招标中是根据技术、商务、报价三项评分标准进行综合评分的,按照综合得分的高低进行排序,排序高者中标。分值权重表如下:
综合得分 技术 商务 报价
技术标、商务标基本都是由公司的技术、资质、资信等实力来决定的。报价标则相对灵活,报价标的评分方法是:基准价的基准分是分,若报价每高于基准价,则在基准分的基础上扣分,最低得分分;若报价每低于基准价,则在基准分的基础上加分,最高得分为分。若报价低于基准价以上(不含)每再低,在分在基础上扣分。在某次招标中,若基准价为(万元),甲、乙两公司综合得分如下表:
公司 技术 商务 报价
甲 分 分 分
乙 分 分 分
甲公司的报价为(万元),乙公司的报价为(万元),则甲、乙两公司综合得分分别是
(A) (B)
(C) (D)
第二部分(非选择题 共110分)
二、填空题(本大题共5小题,每小题5分,满分25分。)
(11)双曲线的一条渐近线为,则的焦距为 .
(12)已知为平面上的动点,,为平面上两个定点,且,则动点的轨迹方程为 .
(13)函数的图像向左平移 个长度单位得到函数的图像,若函数在区间单调递增,则的最大值为 .
(14)在梯形中,,,,
,是的中点,则= .
(15)已知函数为奇函数,且,当时,,给出下列四个结论:
①图像关于对称
②图像关于直线对称
③
④在区间单调递减
其中所有正确结论的序号是 .
三、解答题(本大题共6小题,满分85分。解答应写出文字说明、演算步骤或证明。)
(16)(本小题满分12分)
在中,.
(Ⅰ)求;
(Ⅱ)若,从条件①、条件②、条件③中任选一个作为已知,使存在并唯一确定,并求的值.
条件①:
条件②:
条件③:
注:如果选择的条件不符合要求,第(Ⅱ)问得0分;如果选择多个符合要求的条件分别解答,按第一个解答计分.
(17)(本小题满分15分)
如图,在四棱锥中,底面为梯形,,,,,,,分别为,的中点.
(Ⅰ)判断直线与的位置关系,并说明理由;
(Ⅱ)求二面角的余弦值;
(Ⅲ)求点到平面的距离.
(18)(本小题满分13分)
第24届冬季奥运会将于2022年2月在北京和张家口举办. 为了普及冬奥知识,京西某校组织全体学生进行了冬奥知识答题比赛,从高一年级(共六个班)答题优秀的学生中随机抽查了名,得到这名优秀学生的统计如下:
高一班级 一(1) 一(2) 一(3) 一(4) 一(5) 一(6)
人数
(Ⅰ)从这名学生中随机抽取两名学生参加区里冬奥知识比赛.
()恰好这名学生都来自同一班级的概率是多少?
()设这名学生中来自高一(2)的人数为,求的分布列及数学期望;
(Ⅱ)如果该校高中生的优秀率为,从该校中随机抽取人,这两人中优秀的人数为,求的期望.
(19)(本小题满分15分)
已知函数.
(Ⅰ)求在点处的切线方程;
(Ⅱ)证明:在区间存在唯一极大值点;
(Ⅲ)证明:当,.
(20)(本小题满分15分)
已知椭圆的离心率为,长轴的两个端点分别为.
(Ⅰ)求的方程;
(Ⅱ)设直线与分别相交于两点,直线与相交于点.试问:当 变化时,点是否恒在一条定直线上若是,请写出这条直线方程,并证明你的结论;若不是,请说明理由.
(21)(本小题满分15分)
若集合()满足:对任意(),均存在(),使得,则称具有性质.
(Ⅰ)判断集合,是否具有性质;(只需写出结论)
(Ⅱ)已知集合()具有性质.
()求;
()证明:.
门头沟区2021-2022学年第一学期期末调研高三
数学答案解析
(1)复数
(A) (B) (C) (D)
解:直接计算可得(A)
(2)集合,,则
(A) (B)
(C) (D)
解:易得(C)
(3)在的展开式中,的系数是
(A) (B) (C) (D)
解:由通项公式直接计算得(B)
(4) “角的终边关于轴对称”是“”的
(A)充分不必要条件 (B)必要不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
解:由三角函数的定义可得(A)
(5)下列函数中,在为增函数的是
(A) (B) (C) (D)
解:A不正确,在每一个单调区间上增,在不是增函数;B是对称轴为,在不是增函数;C在为减函数,D求导得可,可知(D)正确
(A) (B) (C) (D)
(6)如图,在下列四个正方体中,为正方体的两个顶点,为所在棱的中点,则在这四个正方体中,直线与平面不垂直的是
(A) (B)
(C) (D)
解:由线面垂直判定定理可得A,B,C都符合直线与平面垂直,但D中的与所成的角为,选择(D)
(7)等差数列的公差,数列的前项和,则
(A) (B)
(C) (D)
解:设,则,当时,,得,,选择(C)
(8)点在抛物线上,则到直线的距离与到直线的距离之和的最小值为
(A) (B) (C) (D)
解:由定义得此最小值就是焦点到直线的距离,由点到直线距离得(B)
(9)在函数的图像上存在两个不同点,使得关于直线的对称点在函数的图像上,则实数的取值范围是
(A) (B) (C) (D)
解:由指对函数性质可知,其实就是研究函数与
函数是否有二个不同交点,当时,
不合 题意;当时,,
有二个交点 得(C)
(10)公司在工程招标中是根据技术、商务、报价三项评分标准进行综合评分的,按照综合得分的高低进行排序,排序高者中标。分值权重表如下:
综合得分 技术 商务 报价
技术标、商务标基本都是由公司的技术、资质、资信等实力来决定的。报价标则相对灵活,报价标的评分方法是:基准价的基准分是分,若报价每高于基准价,则在基准分的基础上扣分,最低得分分;若报价每低于基准价,则在基准分的基础上加分,最高得分为分。若报价低于基准价以上(不含)每再低,在分在基础上扣分。在某次招标中,若基准价为(万元),甲、乙两公司综合得分如下表:
公司 技术 商务 报价
甲 分 分 分
乙 分 分 分
甲公司的报价为(万元),乙公司的报价为(万元),则甲、乙两公司综合得分分别是
(A) (B)
(C) (D)
解:由题意分析可得(A)
二、填空题(本大题共5小题,每小题5分,满分25分。)
(11)双曲线的一条渐近线为,则的焦距为 .
解:
(12)已知为平面上的动点,,为平面上两个定点,且,则动点的轨迹方程为 .
解:由数量积定义得:
(13)函数的图像向左平移 个长度单位得到函数的图像,若函数在区间单调递增,则的最大值为 .
解:(写出符合条件的一个值即可);
(14)在梯形中,,,
,,是的中点,则
= .
解:思考一:投影法=14
思考二:几何运算:
思考三:坐标法:以中点为原点,所在直线为轴,用坐标运算也可。
(15)已知函数为奇函数,且,当时,,给出下列四个结论:
①图像关于对称
②图像关于直线对称
③
④在区间单调递减
其中所有正确结论的序号是 .
解:函数为奇函数得:
可得图像关于关于对称;由得
,所以①正确,②正确;
,所以③不正确;④正确.
所以,正确题目的顺序号为①②④
三、解答题(本大题共6小题,满分85分。解答应写出文字说明、演算步骤或证明。)
(16)(本小题满分12分)
在中,.
(Ⅰ)求;
(Ⅱ)若,从条件①、条件②、条件③中任选一个作为已知,使存在并唯一确定,并求的值.
条件①:
条件②:
条件③:
注:如果选择的条件不符合要求,第(Ⅱ)问得0分;如果选择多个符合要求的条件分别解答,按第一个解答计分.
解:(Ⅰ)由正弦定理得
……………2分
所以……………………………………………………2分
(Ⅱ)选条件②
由正弦定理得:……………………………………2分
…………………………………………2分
………………………………………………2 分
………………………………………………2分
注:若利用余弦定理,结论正确同样可得满分。
选条件③
……………………………………………………2分
…………………………………………………2分
…………………………………………………4分
(17)(本小题满分15分)
如图,在四棱锥中,底面为梯形,,,,,,,分别为,的中点.
(Ⅰ)判断直线与的位置关系,并说明理由;
(Ⅱ)求二面角的余弦值;
(Ⅲ)求点到平面的距离.
解:(Ⅰ).
连结,因为分别是,的中点,所以………….…..…1分
又因为,所以,………………………………………………1分
所以四边形为平行四边形,故………………………………………1分
注:回答与共面,也给满分。
(Ⅱ)由已知两两垂直,建立如图所示坐标系………………………….……1分
……………2分
设平面法向量为,
..2分
平面的法向量为…………1分
……………2分
二面角的余弦值为…………………………………………..………1分
(Ⅲ),……………………………………………………..………1分
设点到平面的距离为,则……………………………2分
(18)(本小题满分13分)
第24届冬季奥运会将于2022年2月在北京和张家口举办. 为了普及冬奥知识,京西某校组织全体学生进行了冬奥知识答题比赛,从高一年级(共六个班)答题优秀的学生中随机抽查了名,得到这名优秀学生的统计如下:
高一班级 一(1) 一(2) 一(3) 一(4) 一(5) 一(6)
人数
(Ⅰ)从这名学生中随机抽取2名学生参加区里冬奥知识比赛.
()恰好这名学生都来自同一班级的概率是多少?
()设这名学生中来自高一(2)的人数为,求的分布列及数学期望;
(Ⅱ)如果该校高中生的优秀率为,从该校中随机抽取人,这两人中优秀的人数为,求的期望.
解:(Ⅰ)()20名学生中随机抽取两名学生共有…………………..……..…2分
设恰好2名学生都来自同一班级共有………....…1分
……………………………………………………………..…1分
注:如果没有设,有答不扣分,没有设,也没有答扣1分
()可取0,1,2,……………………………………………………………1分
,,………...3分
的分布列为:
0 1 2
…………………………...…1分
的期望……………………………………….……..…1分
(Ⅱ)可取0,1,2,…………………………………………………………………1分
,所以……………………………........…………2分
注:只写出,不扣分.
(19)(本小题满分15分)
已知函数.
(Ⅰ)求在点处的切线方程;
(Ⅱ)证明:在区间存在唯一极大值点;
(Ⅲ)证明:当,.
解:(Ⅰ)……………………………………….…………….………2分
,,得切线方程为………………………………2分
(Ⅱ)由(Ⅰ)得,时,…………………..1分
时,单调递减,,,…………2分
由零点存在定理可得,在存在唯一一个零点,…………1分
且当,,
所以,在区间存在唯一极大值点.………………………………2分
(Ⅲ)由(Ⅱ)可知,在区间上单调递增,在单调递减,…….1分
,,所以,当时,………….…2分
当时,.…………...………2分
(20)(本小题满分15分)
已知椭圆的离心率为,长轴的两个端点分别为.
(Ⅰ)求的方程;
(Ⅱ)设直线与分别相交于两点,直线与相交于点.试问:当 变化时,点是否恒在一条定直线上若是,请写出这条直线方程,并证明你的结论;若不是,请说明理由.
解:(Ⅰ)由题意得:.……………………….……..…3分
(Ⅱ)若,与椭圆相交于.……….…1分
直线:,直线.…………………………1分
.…………………………………………….…………1分
由椭圆的对称性若可得交点为.………...………1分
当变化时,点恒在定直线上.……………………………… …………1分
若时,.……………………………1分
设交点为,由韦达定理得:(1)…...…….1分
直线:与定直线相交于,得..….1分
同理直与直线相交于,得.…..1分
.……2分
(1)式代入得,所以当变化时,点恒在一条定直线上.………1分
(21)(本小题满分15分)
若集合()满足:对任意(),均存在(),使得,则称具有性质.
(Ⅰ)判断集合,是否具有性质;(只需写出结论)
(Ⅱ)已知集合()具有性质.
()求;
()证明:.
解:(Ⅰ)集合具有性质;……………………………………………………...……2分
集合不具有性质.………………………………………………... ………2分
(Ⅱ)()取,由题知存在(),使得成立,即,………..…2分
又,故必有.…………...………….……………………2分
又因为,所以.……..……………..…1分
()由()得,当时,存在()使得成立,又因为,故,即.所以.….……2分
又,所以,
故,…………….. 2分
相加得:
,即.
………….……2分
高三数学试卷 第 1 页 (共 3 页)
高 三 数学 2022.1
考 生 须 知 1.本试卷共6页,共3道大题,21个小题。满分100分。考试时间90分钟。 2.在试卷和答题卡上准确填写学校和姓名,并将考试编号填写(或条形码粘贴)在答题卡相应位置处。 3.试题答案一律填涂或书写在答题卡上,在试卷上作答无效。选择题、作图题用2B铅笔作答,其它试题用黑色字迹签字笔作答。 4.考试结束,将试卷、答题卡和草稿纸一并交回。
第一部分(选择题 共40分)
一、选择题(本大题共10个小题,每小题4分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。)
(1)复数
(A) (B)
(C) (D)
(2)集合,,则
(A) (B)
(C) (D)
(3)在的展开式中,的系数是
(A) (B)
(C) (D)
(4) “角的终边关于轴对称”是“”的
(A)充分不必要条件 (B)必要不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
(5)下列函数中,在为增函数的是
(A) (B)
(C) (D)
(6)如图,在下列四个正方体中,为正方体的两个顶点,为所在棱的中点,则在这四个正方体中,直线与平面不垂直的是
(A) (B)
(C) (D)
(7)等差数列的公差,数列的前项和,则
(A) (B)
(C) (D)
(8)点在抛物线上,则到直线的距离与到直线的距离之和的最小值为
(A) (B)
(C) (D)
(9)在函数的图像上存在两个不同点,使得关于直线的对称点在函数的图像上,则实数的取值范围是
(A) (B)
(C) (D)
(10)公司在工程招标中是根据技术、商务、报价三项评分标准进行综合评分的,按照综合得分的高低进行排序,排序高者中标。分值权重表如下:
综合得分 技术 商务 报价
技术标、商务标基本都是由公司的技术、资质、资信等实力来决定的。报价标则相对灵活,报价标的评分方法是:基准价的基准分是分,若报价每高于基准价,则在基准分的基础上扣分,最低得分分;若报价每低于基准价,则在基准分的基础上加分,最高得分为分。若报价低于基准价以上(不含)每再低,在分在基础上扣分。在某次招标中,若基准价为(万元),甲、乙两公司综合得分如下表:
公司 技术 商务 报价
甲 分 分 分
乙 分 分 分
甲公司的报价为(万元),乙公司的报价为(万元),则甲、乙两公司综合得分分别是
(A) (B)
(C) (D)
第二部分(非选择题 共110分)
二、填空题(本大题共5小题,每小题5分,满分25分。)
(11)双曲线的一条渐近线为,则的焦距为 .
(12)已知为平面上的动点,,为平面上两个定点,且,则动点的轨迹方程为 .
(13)函数的图像向左平移 个长度单位得到函数的图像,若函数在区间单调递增,则的最大值为 .
(14)在梯形中,,,,
,是的中点,则= .
(15)已知函数为奇函数,且,当时,,给出下列四个结论:
①图像关于对称
②图像关于直线对称
③
④在区间单调递减
其中所有正确结论的序号是 .
三、解答题(本大题共6小题,满分85分。解答应写出文字说明、演算步骤或证明。)
(16)(本小题满分12分)
在中,.
(Ⅰ)求;
(Ⅱ)若,从条件①、条件②、条件③中任选一个作为已知,使存在并唯一确定,并求的值.
条件①:
条件②:
条件③:
注:如果选择的条件不符合要求,第(Ⅱ)问得0分;如果选择多个符合要求的条件分别解答,按第一个解答计分.
(17)(本小题满分15分)
如图,在四棱锥中,底面为梯形,,,,,,,分别为,的中点.
(Ⅰ)判断直线与的位置关系,并说明理由;
(Ⅱ)求二面角的余弦值;
(Ⅲ)求点到平面的距离.
(18)(本小题满分13分)
第24届冬季奥运会将于2022年2月在北京和张家口举办. 为了普及冬奥知识,京西某校组织全体学生进行了冬奥知识答题比赛,从高一年级(共六个班)答题优秀的学生中随机抽查了名,得到这名优秀学生的统计如下:
高一班级 一(1) 一(2) 一(3) 一(4) 一(5) 一(6)
人数
(Ⅰ)从这名学生中随机抽取两名学生参加区里冬奥知识比赛.
()恰好这名学生都来自同一班级的概率是多少?
()设这名学生中来自高一(2)的人数为,求的分布列及数学期望;
(Ⅱ)如果该校高中生的优秀率为,从该校中随机抽取人,这两人中优秀的人数为,求的期望.
(19)(本小题满分15分)
已知函数.
(Ⅰ)求在点处的切线方程;
(Ⅱ)证明:在区间存在唯一极大值点;
(Ⅲ)证明:当,.
(20)(本小题满分15分)
已知椭圆的离心率为,长轴的两个端点分别为.
(Ⅰ)求的方程;
(Ⅱ)设直线与分别相交于两点,直线与相交于点.试问:当 变化时,点是否恒在一条定直线上若是,请写出这条直线方程,并证明你的结论;若不是,请说明理由.
(21)(本小题满分15分)
若集合()满足:对任意(),均存在(),使得,则称具有性质.
(Ⅰ)判断集合,是否具有性质;(只需写出结论)
(Ⅱ)已知集合()具有性质.
()求;
()证明:.
门头沟区2021-2022学年第一学期期末调研高三
数学答案解析
(1)复数
(A) (B) (C) (D)
解:直接计算可得(A)
(2)集合,,则
(A) (B)
(C) (D)
解:易得(C)
(3)在的展开式中,的系数是
(A) (B) (C) (D)
解:由通项公式直接计算得(B)
(4) “角的终边关于轴对称”是“”的
(A)充分不必要条件 (B)必要不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
解:由三角函数的定义可得(A)
(5)下列函数中,在为增函数的是
(A) (B) (C) (D)
解:A不正确,在每一个单调区间上增,在不是增函数;B是对称轴为,在不是增函数;C在为减函数,D求导得可,可知(D)正确
(A) (B) (C) (D)
(6)如图,在下列四个正方体中,为正方体的两个顶点,为所在棱的中点,则在这四个正方体中,直线与平面不垂直的是
(A) (B)
(C) (D)
解:由线面垂直判定定理可得A,B,C都符合直线与平面垂直,但D中的与所成的角为,选择(D)
(7)等差数列的公差,数列的前项和,则
(A) (B)
(C) (D)
解:设,则,当时,,得,,选择(C)
(8)点在抛物线上,则到直线的距离与到直线的距离之和的最小值为
(A) (B) (C) (D)
解:由定义得此最小值就是焦点到直线的距离,由点到直线距离得(B)
(9)在函数的图像上存在两个不同点,使得关于直线的对称点在函数的图像上,则实数的取值范围是
(A) (B) (C) (D)
解:由指对函数性质可知,其实就是研究函数与
函数是否有二个不同交点,当时,
不合 题意;当时,,
有二个交点 得(C)
(10)公司在工程招标中是根据技术、商务、报价三项评分标准进行综合评分的,按照综合得分的高低进行排序,排序高者中标。分值权重表如下:
综合得分 技术 商务 报价
技术标、商务标基本都是由公司的技术、资质、资信等实力来决定的。报价标则相对灵活,报价标的评分方法是:基准价的基准分是分,若报价每高于基准价,则在基准分的基础上扣分,最低得分分;若报价每低于基准价,则在基准分的基础上加分,最高得分为分。若报价低于基准价以上(不含)每再低,在分在基础上扣分。在某次招标中,若基准价为(万元),甲、乙两公司综合得分如下表:
公司 技术 商务 报价
甲 分 分 分
乙 分 分 分
甲公司的报价为(万元),乙公司的报价为(万元),则甲、乙两公司综合得分分别是
(A) (B)
(C) (D)
解:由题意分析可得(A)
二、填空题(本大题共5小题,每小题5分,满分25分。)
(11)双曲线的一条渐近线为,则的焦距为 .
解:
(12)已知为平面上的动点,,为平面上两个定点,且,则动点的轨迹方程为 .
解:由数量积定义得:
(13)函数的图像向左平移 个长度单位得到函数的图像,若函数在区间单调递增,则的最大值为 .
解:(写出符合条件的一个值即可);
(14)在梯形中,,,
,,是的中点,则
= .
解:思考一:投影法=14
思考二:几何运算:
思考三:坐标法:以中点为原点,所在直线为轴,用坐标运算也可。
(15)已知函数为奇函数,且,当时,,给出下列四个结论:
①图像关于对称
②图像关于直线对称
③
④在区间单调递减
其中所有正确结论的序号是 .
解:函数为奇函数得:
可得图像关于关于对称;由得
,所以①正确,②正确;
,所以③不正确;④正确.
所以,正确题目的顺序号为①②④
三、解答题(本大题共6小题,满分85分。解答应写出文字说明、演算步骤或证明。)
(16)(本小题满分12分)
在中,.
(Ⅰ)求;
(Ⅱ)若,从条件①、条件②、条件③中任选一个作为已知,使存在并唯一确定,并求的值.
条件①:
条件②:
条件③:
注:如果选择的条件不符合要求,第(Ⅱ)问得0分;如果选择多个符合要求的条件分别解答,按第一个解答计分.
解:(Ⅰ)由正弦定理得
……………2分
所以……………………………………………………2分
(Ⅱ)选条件②
由正弦定理得:……………………………………2分
…………………………………………2分
………………………………………………2 分
………………………………………………2分
注:若利用余弦定理,结论正确同样可得满分。
选条件③
……………………………………………………2分
…………………………………………………2分
…………………………………………………4分
(17)(本小题满分15分)
如图,在四棱锥中,底面为梯形,,,,,,,分别为,的中点.
(Ⅰ)判断直线与的位置关系,并说明理由;
(Ⅱ)求二面角的余弦值;
(Ⅲ)求点到平面的距离.
解:(Ⅰ).
连结,因为分别是,的中点,所以………….…..…1分
又因为,所以,………………………………………………1分
所以四边形为平行四边形,故………………………………………1分
注:回答与共面,也给满分。
(Ⅱ)由已知两两垂直,建立如图所示坐标系………………………….……1分
……………2分
设平面法向量为,
..2分
平面的法向量为…………1分
……………2分
二面角的余弦值为…………………………………………..………1分
(Ⅲ),……………………………………………………..………1分
设点到平面的距离为,则……………………………2分
(18)(本小题满分13分)
第24届冬季奥运会将于2022年2月在北京和张家口举办. 为了普及冬奥知识,京西某校组织全体学生进行了冬奥知识答题比赛,从高一年级(共六个班)答题优秀的学生中随机抽查了名,得到这名优秀学生的统计如下:
高一班级 一(1) 一(2) 一(3) 一(4) 一(5) 一(6)
人数
(Ⅰ)从这名学生中随机抽取2名学生参加区里冬奥知识比赛.
()恰好这名学生都来自同一班级的概率是多少?
()设这名学生中来自高一(2)的人数为,求的分布列及数学期望;
(Ⅱ)如果该校高中生的优秀率为,从该校中随机抽取人,这两人中优秀的人数为,求的期望.
解:(Ⅰ)()20名学生中随机抽取两名学生共有…………………..……..…2分
设恰好2名学生都来自同一班级共有………....…1分
……………………………………………………………..…1分
注:如果没有设,有答不扣分,没有设,也没有答扣1分
()可取0,1,2,……………………………………………………………1分
,,………...3分
的分布列为:
0 1 2
…………………………...…1分
的期望……………………………………….……..…1分
(Ⅱ)可取0,1,2,…………………………………………………………………1分
,所以……………………………........…………2分
注:只写出,不扣分.
(19)(本小题满分15分)
已知函数.
(Ⅰ)求在点处的切线方程;
(Ⅱ)证明:在区间存在唯一极大值点;
(Ⅲ)证明:当,.
解:(Ⅰ)……………………………………….…………….………2分
,,得切线方程为………………………………2分
(Ⅱ)由(Ⅰ)得,时,…………………..1分
时,单调递减,,,…………2分
由零点存在定理可得,在存在唯一一个零点,…………1分
且当,,
所以,在区间存在唯一极大值点.………………………………2分
(Ⅲ)由(Ⅱ)可知,在区间上单调递增,在单调递减,…….1分
,,所以,当时,………….…2分
当时,.…………...………2分
(20)(本小题满分15分)
已知椭圆的离心率为,长轴的两个端点分别为.
(Ⅰ)求的方程;
(Ⅱ)设直线与分别相交于两点,直线与相交于点.试问:当 变化时,点是否恒在一条定直线上若是,请写出这条直线方程,并证明你的结论;若不是,请说明理由.
解:(Ⅰ)由题意得:.……………………….……..…3分
(Ⅱ)若,与椭圆相交于.……….…1分
直线:,直线.…………………………1分
.…………………………………………….…………1分
由椭圆的对称性若可得交点为.………...………1分
当变化时,点恒在定直线上.……………………………… …………1分
若时,.……………………………1分
设交点为,由韦达定理得:(1)…...…….1分
直线:与定直线相交于,得..….1分
同理直与直线相交于,得.…..1分
.……2分
(1)式代入得,所以当变化时,点恒在一条定直线上.………1分
(21)(本小题满分15分)
若集合()满足:对任意(),均存在(),使得,则称具有性质.
(Ⅰ)判断集合,是否具有性质;(只需写出结论)
(Ⅱ)已知集合()具有性质.
()求;
()证明:.
解:(Ⅰ)集合具有性质;……………………………………………………...……2分
集合不具有性质.………………………………………………... ………2分
(Ⅱ)()取,由题知存在(),使得成立,即,………..…2分
又,故必有.…………...………….……………………2分
又因为,所以.……..……………..…1分
()由()得,当时,存在()使得成立,又因为,故,即.所以.….……2分
又,所以,
故,…………….. 2分
相加得:
,即.
………….……2分
高三数学试卷 第 1 页 (共 3 页)
同课章节目录
