新人教版九年级上册24.2.2 直线和圆的位置关系(2)
文档属性
| 名称 | 新人教版九年级上册24.2.2 直线和圆的位置关系(2) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-15 21:44:48 | ||
图片预览







文档简介
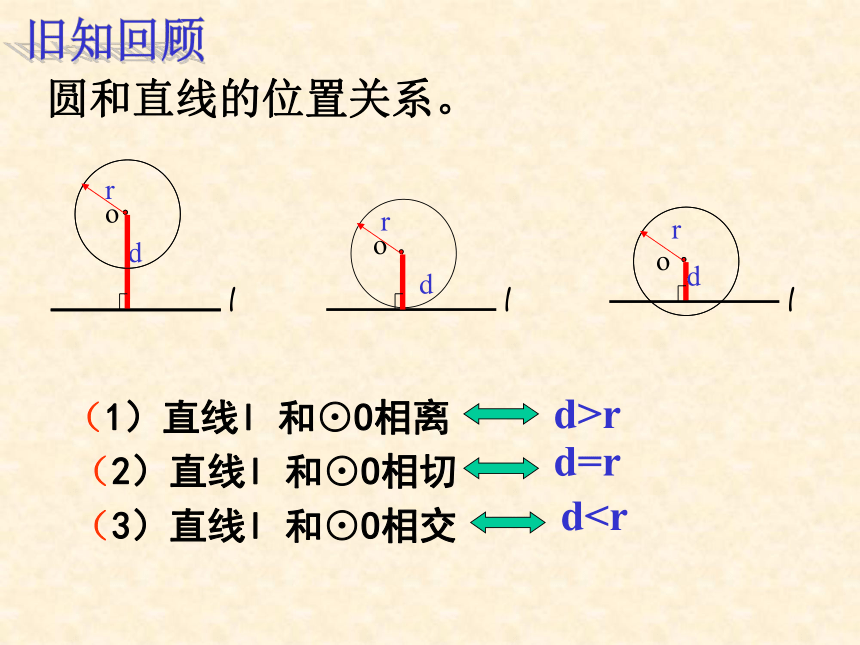
课件32张PPT。直线与圆的位置关系(2)“大漠孤烟直,长河落日圆”(2)直线l 和⊙O相切圆和直线的位置关系。 (1)直线l 和⊙O相离(3)直线l 和⊙O相交d>rd=rd图中直线l是⊙O的切线,怎样判定?答:①直线与圆有唯一公共点;
②直线到圆心的距离等于该圆的半径;
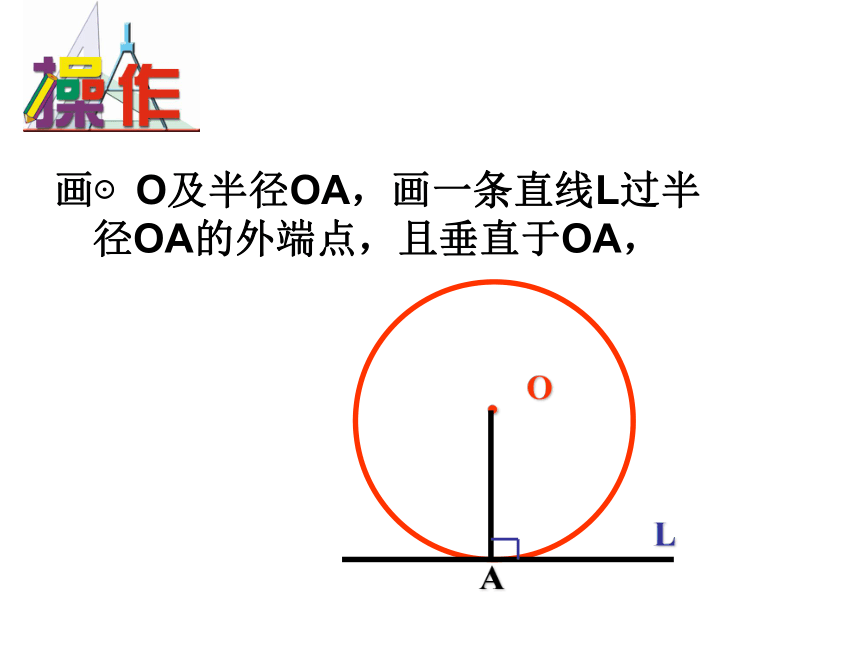
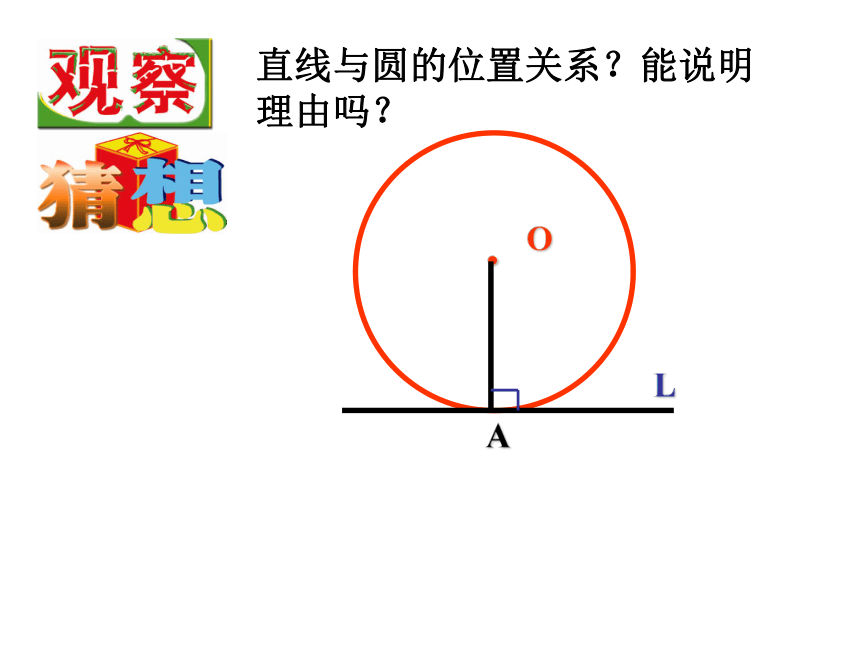
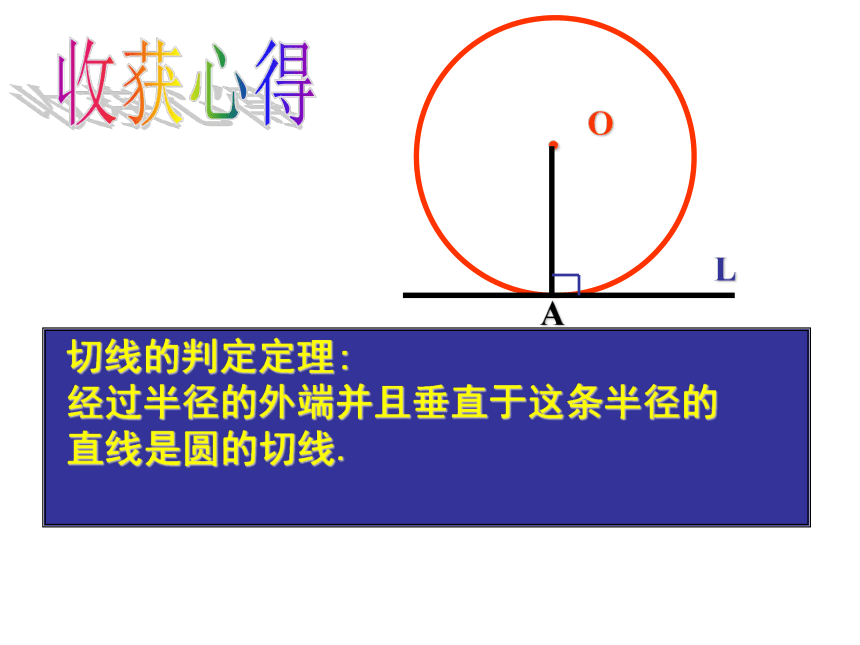
思考判定一条直线是不是圆的切线除了这两种 方法外还有其它方法吗?.OAL画⊙O及半径OA,画一条直线L过半径OA的外端点,且垂直于OA,直线与圆的位置关系?能说明理由吗?.OAL.OAL切线的判定定理:
经过半径的外端并且垂直于这条半径的
直线是圆的切线.收获心得(二)切线的判定定理:
1、切线的判定定理:经过半径外端并且垂直于这条半径的直线是圆的切线.2、对定理的理解:切线需满足两条: ①经过半径外端.②垂直于这条半径. 注意:定理中的两个条件缺一不可. 问题1:下雨天,转动的雨伞上的水滴是
顺着伞的什么方向飞出去的?问题2:砂轮转动时,火花是沿着砂轮的
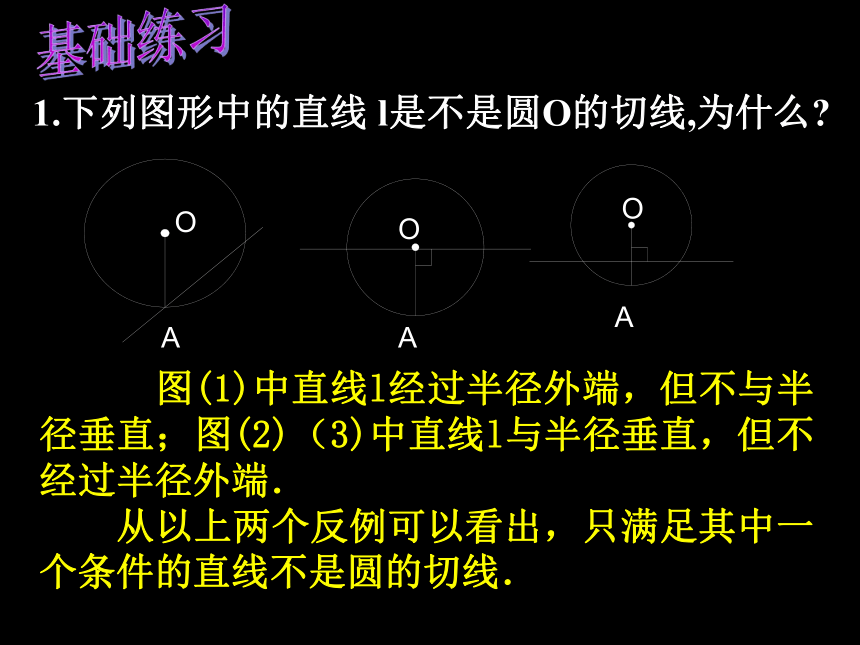
什么方向飞出去的? 图(1)中直线l经过半径外端,但不与半径垂直;图(2)(3)中直线l与半径垂直,但不经过半径外端.
从以上两个反例可以看出,只满足其中一个条件的直线不是圆的切线.
1.下列图形中的直线 l是不是圆O的切线,为什么?基础练习AAOAOO2.判断下列命题是否正确.
(1)经过半径外端的直线是圆的切线.( )
(2)垂直于半径的直线是圆的切线.( )
(3)过直径的外端并且垂直于这条直径的直线是圆的切线.( )
(4)和圆有一个公共点的直线是圆的切线.( )
(5)以等腰三角形的顶点为圆心,底边上的高为半径的圆与底边相切.( )
错错对错对(三)切线的判定方法切线的判定方法有三种:①直线与圆有唯一公共点;②直线到圆心的距离等于该圆的半径;③切线的判定定理.(四)应用定理.
例1 已知:直线AB经过⊙O上的点C,
并且OA=OB,CA=CB.
求证:直线AB是⊙O的切线. 直线AB经过半径0C的外端C,并且垂直于半径0C, 所以AB是⊙O的切线. ABCO证明:连结0C∵0A=0B,CA=CB,∴0C是等腰三角形0AB底边AB上的中线.∴AB⊥OC.方法小结: 证明过圆上一点的直线是圆的切线.只要证明这条直线垂直于经过切点的半径.例2.如图,线段AB经过圆心O,交⊙O于点A,C,∠BAD=∠B=30°,边BD交圆于点D。
求证:BD是⊙O的切线证明:连结OD∵ OA=OD , ∴ OD⊥BD又∵直线BD 经过⊙O上的D点∴直线BD是⊙O的切线∴∠ODA=∠A=300ABCD∴∠BDO=90°1.如图, AB是⊙O的直径,∠ABT=45° AT=AB
求证:AT是⊙O的切线 解:∵ AT=AB , ∠ABT=450∴ AT⊥AB又∵直线AT经过⊙O 上的A点∴直线AT是⊙O的切线∴∠T=∠B=450∴∠ BAT =90°BT0A练习2 如图,AB是⊙O的直径,点D在AB的延长线 上,BD=OB,点C在圆上,∠A=300.
求证:DC是⊙O的切线.方法引导
当已知直线与圆有公共点,要证明直线与圆相切时,可先连结圆心与公共点,再证明连线垂直于直线 ,这是证明切线的一种重要方法.练习3、已知:在△ABC中,AB=AC,以AB为直径作⊙O交BC于D,DE⊥AC于E,如图,
求证:DE是⊙O的切线。 例3、如图⊙O的半径为8,弦AB= ,以O为圆心,4为半径作小圆,求证:AB与小圆O相切.证明:
过O作OC⊥AB于C,连结OA证明直线和圆相切的类型二:
无交点,作垂直,证等于半径.2.如图,点D是∠AOB的平分线OC上任意一点,过D作DE⊥OB于E,以DE为半径作⊙D,判断⊙D与OA的位置关系,
并证明你的结论。证明直线与圆相切,但无切点时,往往过圆心作切线的垂线,再证明d=r即可F1、定义法:和圆有且只有一个公共点的直线是圆的切线。
2、数量法(d=r):和圆心距离等于半径的直线是圆的切线。
3、判定定理:经过半径外端且垂直于这条半径的直线是圆的切线。证明直线与圆相切有如下三种途径:即:若直线与圆的一个公共点已指明,则连接这点和圆心,说明直线垂直于经过这点的半径;若直线与圆的公共点未指明,则过圆心作直线的垂线段,然后说明这条线段的长等于圆的半径..OAL已知直线L 是⊙O的切线,切点为A,连接0A,你发现了什么?切线的性质定理:圆的切线垂直于过切点的半径。收获心得.OAL①过半径外端
②垂直于这条半径。切线①圆的切线
②过切点的半径。切线垂直于半径判定定理:性质定理:
例:如图的两个圆是以O为圆心的同心圆,大圆的弦AB是小圆的切线, C为切点.求证:C是AB的中点.CABO证明:如图,∴ C是AB的中点.AC=BC根据垂径定理,得OC⊥AB连接OC, 则若AB=4.能求圆环的面积吗?Rr例:在Rt△ABC的斜边上,以AD为直径的⊙O和BC相切于点F, ⊙O和AC交于E
求证:弧EF=弧FDDCOFBA.E1如图, ⊙O切PB于点B,PB=4,PA=2,则
⊙O的半径多少?2 如图:PA,PC分别切圆O于点A,C两点,B为圆O上与A,C不重合的点,若∠P=50°,则∠ABC=___自我检验求证:经过直径两端点的切线互相平行练习3 已知:如图,AB 是⊙O的直径,AC、BD是⊙O的切线.
证明:如图,AB 是⊙O的直径AC、BD是⊙O的切线AB⊥ACAB⊥BDAC∥BD求证: AC∥BD⊙O 是△APC的外接圆,BD是
⊙O的切线,切点为A,∠C=500
则∠PAD=______DCOPBA.切线的判定方法有三种:①直线与圆有唯一公共点;②直线到圆心的距离等于该圆的半径;③切线的判定定理.反思与小结性质定理:圆的切线垂直于过切点的半径。再见
②直线到圆心的距离等于该圆的半径;
思考判定一条直线是不是圆的切线除了这两种 方法外还有其它方法吗?.OAL画⊙O及半径OA,画一条直线L过半径OA的外端点,且垂直于OA,直线与圆的位置关系?能说明理由吗?.OAL.OAL切线的判定定理:
经过半径的外端并且垂直于这条半径的
直线是圆的切线.收获心得(二)切线的判定定理:
1、切线的判定定理:经过半径外端并且垂直于这条半径的直线是圆的切线.2、对定理的理解:切线需满足两条: ①经过半径外端.②垂直于这条半径. 注意:定理中的两个条件缺一不可. 问题1:下雨天,转动的雨伞上的水滴是
顺着伞的什么方向飞出去的?问题2:砂轮转动时,火花是沿着砂轮的
什么方向飞出去的? 图(1)中直线l经过半径外端,但不与半径垂直;图(2)(3)中直线l与半径垂直,但不经过半径外端.
从以上两个反例可以看出,只满足其中一个条件的直线不是圆的切线.
1.下列图形中的直线 l是不是圆O的切线,为什么?基础练习AAOAOO2.判断下列命题是否正确.
(1)经过半径外端的直线是圆的切线.( )
(2)垂直于半径的直线是圆的切线.( )
(3)过直径的外端并且垂直于这条直径的直线是圆的切线.( )
(4)和圆有一个公共点的直线是圆的切线.( )
(5)以等腰三角形的顶点为圆心,底边上的高为半径的圆与底边相切.( )
错错对错对(三)切线的判定方法切线的判定方法有三种:①直线与圆有唯一公共点;②直线到圆心的距离等于该圆的半径;③切线的判定定理.(四)应用定理.
例1 已知:直线AB经过⊙O上的点C,
并且OA=OB,CA=CB.
求证:直线AB是⊙O的切线. 直线AB经过半径0C的外端C,并且垂直于半径0C, 所以AB是⊙O的切线. ABCO证明:连结0C∵0A=0B,CA=CB,∴0C是等腰三角形0AB底边AB上的中线.∴AB⊥OC.方法小结: 证明过圆上一点的直线是圆的切线.只要证明这条直线垂直于经过切点的半径.例2.如图,线段AB经过圆心O,交⊙O于点A,C,∠BAD=∠B=30°,边BD交圆于点D。
求证:BD是⊙O的切线证明:连结OD∵ OA=OD , ∴ OD⊥BD又∵直线BD 经过⊙O上的D点∴直线BD是⊙O的切线∴∠ODA=∠A=300ABCD∴∠BDO=90°1.如图, AB是⊙O的直径,∠ABT=45° AT=AB
求证:AT是⊙O的切线 解:∵ AT=AB , ∠ABT=450∴ AT⊥AB又∵直线AT经过⊙O 上的A点∴直线AT是⊙O的切线∴∠T=∠B=450∴∠ BAT =90°BT0A练习2 如图,AB是⊙O的直径,点D在AB的延长线 上,BD=OB,点C在圆上,∠A=300.
求证:DC是⊙O的切线.方法引导
当已知直线与圆有公共点,要证明直线与圆相切时,可先连结圆心与公共点,再证明连线垂直于直线 ,这是证明切线的一种重要方法.练习3、已知:在△ABC中,AB=AC,以AB为直径作⊙O交BC于D,DE⊥AC于E,如图,
求证:DE是⊙O的切线。 例3、如图⊙O的半径为8,弦AB= ,以O为圆心,4为半径作小圆,求证:AB与小圆O相切.证明:
过O作OC⊥AB于C,连结OA证明直线和圆相切的类型二:
无交点,作垂直,证等于半径.2.如图,点D是∠AOB的平分线OC上任意一点,过D作DE⊥OB于E,以DE为半径作⊙D,判断⊙D与OA的位置关系,
并证明你的结论。证明直线与圆相切,但无切点时,往往过圆心作切线的垂线,再证明d=r即可F1、定义法:和圆有且只有一个公共点的直线是圆的切线。
2、数量法(d=r):和圆心距离等于半径的直线是圆的切线。
3、判定定理:经过半径外端且垂直于这条半径的直线是圆的切线。证明直线与圆相切有如下三种途径:即:若直线与圆的一个公共点已指明,则连接这点和圆心,说明直线垂直于经过这点的半径;若直线与圆的公共点未指明,则过圆心作直线的垂线段,然后说明这条线段的长等于圆的半径..OAL已知直线L 是⊙O的切线,切点为A,连接0A,你发现了什么?切线的性质定理:圆的切线垂直于过切点的半径。收获心得.OAL①过半径外端
②垂直于这条半径。切线①圆的切线
②过切点的半径。切线垂直于半径判定定理:性质定理:
例:如图的两个圆是以O为圆心的同心圆,大圆的弦AB是小圆的切线, C为切点.求证:C是AB的中点.CABO证明:如图,∴ C是AB的中点.AC=BC根据垂径定理,得OC⊥AB连接OC, 则若AB=4.能求圆环的面积吗?Rr例:在Rt△ABC的斜边上,以AD为直径的⊙O和BC相切于点F, ⊙O和AC交于E
求证:弧EF=弧FDDCOFBA.E1如图, ⊙O切PB于点B,PB=4,PA=2,则
⊙O的半径多少?2 如图:PA,PC分别切圆O于点A,C两点,B为圆O上与A,C不重合的点,若∠P=50°,则∠ABC=___自我检验求证:经过直径两端点的切线互相平行练习3 已知:如图,AB 是⊙O的直径,AC、BD是⊙O的切线.
证明:如图,AB 是⊙O的直径AC、BD是⊙O的切线AB⊥ACAB⊥BDAC∥BD求证: AC∥BD⊙O 是△APC的外接圆,BD是
⊙O的切线,切点为A,∠C=500
则∠PAD=______DCOPBA.切线的判定方法有三种:①直线与圆有唯一公共点;②直线到圆心的距离等于该圆的半径;③切线的判定定理.反思与小结性质定理:圆的切线垂直于过切点的半径。再见
同课章节目录
