四川省内江市2021-2022学年高二上学期期末检测数学(理科)试题(Word版含答案)
文档属性
| 名称 | 四川省内江市2021-2022学年高二上学期期末检测数学(理科)试题(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 758.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-18 15:53:36 | ||
图片预览


文档简介
内江市2021~2022学年度第一学期高二期末检测题
数学(理科)
1、本试卷包括第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共4页。全卷满分150分,考试时间120分钟。
2、答第Ⅰ卷时,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号;答第Ⅱ卷时,用0.5毫米的黑色签字笔在答题卡规定的区域内作答,字体工整,笔记清楚;不能答在试题卷上。
3、考试结束后,监考人将答题卡收回。
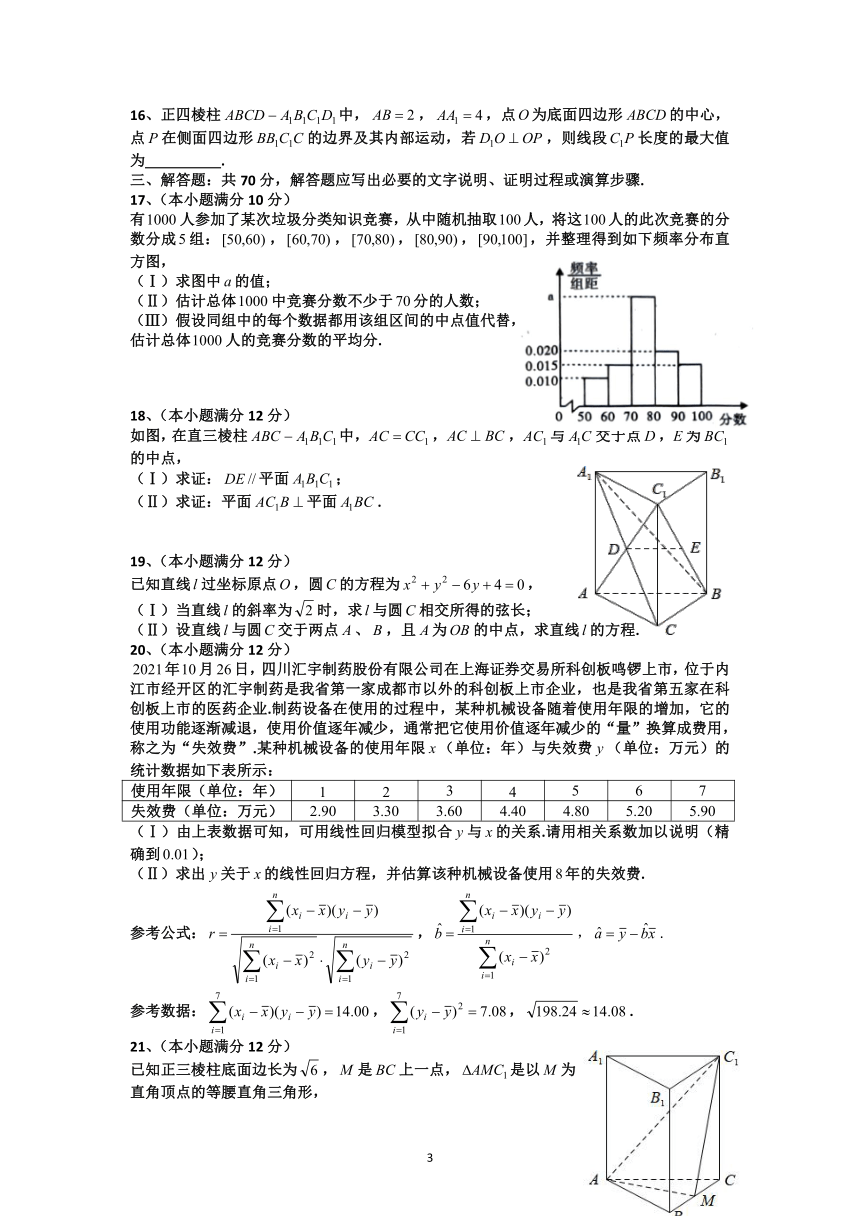
第Ⅰ卷(选择题,共60分)
一、选择题:本大题共12个小题,每小题5分,共60分,每小题有且只有一个正确答案.
1、已知点,点关于原点的对称点为,则
(A) (B) (C) (D)
2、某学校进行新课程改革实验,为了了解名学生对该项新课程改革实验的意见,打算从中抽取一个容量为的样本,采用系统抽烟方法,则分段的间隔为
(A) (B) (C) (D)
3、上海世博会期间,某日时至时累计入园人数的折线图如图所示,那么在时~时,时~时,...,时~时八个时段中,入园人数最多的时段是
(A)时~时 (B)时~时 (C)时~时 (D)时~时
4、某四面体的三视图如图所示,该四面体的面积为
(A) (B) (C) (D)
5、下列四种说法中,正确说法的个数为
①如果两个平面有三个公共点,那么这两个平面重合;
②两条直线可以确定一个平面;
③若,,,则;
④空间中,两两相交的三条直线在同一个平面内
(A) (B) (C) (D)
6、如图,将边长为的正方形折成一个正四棱柱的侧面,则异面
直线和所成角的大小为
(A) (B)
(C) (D)
7、从编号分别为,,,,的五个大小完全相同的小球中,随机取出三个小球,则恰有两个小球编号相邻的概率为
(A) (B) (C) (D)
8、已知实数,满足,则的最大值为
(A) (B) (C) (D)
9、几何学史上有一个著名的米勒问题:“设点、是锐角的一边上的两点,试在边上找一点,使得最大的.”如图,其结论是:点为过、两点且和射线相切的圆的切点.根据以上结论解决一下问题:在平面直角坐标系中,给定两点,,点在轴上移动,当取最大值时,点的横坐标是
(A)
(B)
(C)或
(D)或
10、已知点,,直线:与线段相交,则实数的取值范围是
(A)或 (B)或 (C) (D)
11、在正方体中,为棱上一点,且,若二面角为,则四面体的外接球的表面积为
(A) (B)
(C) (D)
12、已知圆:,点是直线:上的动点,过点引圆的两条切线、,其中、为切点,则直线经过定点
(A) (B) (C) (D)
第Ⅱ卷(非选择题,共90分)
二、填空题:本大题共4个小题,每小题5分,共20分.
13、已知茎叶图记录了甲、乙两组各名学生在一次英语听力测试中的成绩(单位:分).已知甲组数据的中位数为,乙组数据的平均数为,则的值为 .
甲组 乙组
14、过圆内的点作一条直线,使它被该圆截得的线段最短,则直线的方程是 .
15、秦九韶出生于普州(今资阳市安岳县),是我国南宋时期伟大的数学家,他创立的秦九韶算法历来为人称道,其本质是将一个次多项式写成个一次式相组合的形式,如可将写成,由此可得 .
16、正四棱柱中,,,点为底面四边形的中心,点在侧面四边形的边界及其内部运动,若,则线段长度的最大值为 .
三、解答题:共70分,解答题应写出必要的文字说明、证明过程或演算步骤.
17、(本小题满分10分)
有人参加了某次垃圾分类知识竞赛,从中随机抽取人,将这人的此次竞赛的分数分成组:,,,,,并整理得到如下频率分布直方图,
(Ⅰ)求图中的值;
(Ⅱ)估计总体中竞赛分数不少于分的人数;
(Ⅲ)假设同组中的每个数据都用该组区间的中点值代替,
估计总体人的竞赛分数的平均分.
18、(本小题满分12分)
如图,在直三棱柱中,,,与交于点,为的中点,
(Ⅰ)求证:平面;
(Ⅱ)求证:平面平面.
19、(本小题满分12分)
已知直线过坐标原点,圆的方程为,
(Ⅰ)当直线的斜率为时,求与圆相交所得的弦长;
(Ⅱ)设直线与圆交于两点、,且为的中点,求直线的方程.
20、(本小题满分12分)
年月日,四川汇宇制药股份有限公司在上海证券交易所科创板鸣锣上市,位于内江市经开区的汇宇制药是我省第一家成都市以外的科创板上市企业,也是我省第五家在科创板上市的医药企业.制药设备在使用的过程中,某种机械设备随着使用年限的增加,它的使用功能逐渐减退,使用价值逐年减少,通常把它使用价值逐年减少的“量”换算成费用,称之为“失效费”.某种机械设备的使用年限(单位:年)与失效费(单位:万元)的统计数据如下表所示:
使用年限(单位:年)
失效费(单位:万元)
(Ⅰ)由上表数据可知,可用线性回归模型拟合与的关系.请用相关系数加以说明(精确到);
(Ⅱ)求出关于的线性回归方程,并估算该种机械设备使用年的失效费.
参考公式:,,.
参考数据:,,.
21、(本小题满分12分)
已知正三棱柱底面边长为,是上一点,是以为
直角顶点的等腰直角三角形,
(Ⅰ)证明:是的中点;
(Ⅱ)求二面角的大小.
22、(本小题满分12分)
已知圆的圆心在直线上,与轴正半轴相切,且被直线:截得的弦长为,
(Ⅰ)求圆的方程;
(Ⅱ)设点在圆上运动,点,且点满足,记点的轨迹为,
(i)求的方程,并说明是什么图形;
(ii)试探究:在直线上是否存在定点(异于原点),使得对于上任意一点,都有为一常数,若存在,求出所有满足条件的点的坐标,若不存在,请说明理由.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 C B B A A D C A C B C D
二、填空题
13、 14、 15、 16、
三、解答题
17、解:(Ⅰ)由图知:
解得:
(Ⅱ)样本中,,的频率分布为,,
即:样本中分数不少于分的频率为
则估计总体中不少于分的频率为
故估计总体中不少于分的人数为人
(Ⅲ)样本中平均分的估计值为
故估计总体中的平均分为分
18、解:(Ⅰ)在直三棱柱中,
且四边形为平行四边形,又
则为的中点,又为的中点
故,即:,且平面,平面
所以平面
(Ⅱ)在直三棱柱中,平面
则,且,
故平面,即:
又在平行四边形中,
则四边形为菱形,即:,且
故平面,即:平面平面
19、解:(Ⅰ)由题意知:的方程为,即:
圆的方程可化为:,其圆心为,半径为
则到的距离为
故所求弦长为
(Ⅱ)设,,由为的中点知:,
当斜率不存在时,:
联立,则
故,且,得:方程组无解,此时不符合
当斜率存在时,:
联立,则
故,且,解得:
即:为
综上,所求的方程为
(第(Ⅱ)中,可设的方程为,不用讨论)
20、解:(Ⅰ)由表知:
则
故
所以的值非常接近于,即:可用线性回归模型拟合与的关系
(Ⅱ)由表知:
则,
故所求回归方程为
令,则(万元)
所以估计该设备使用年的失效费为万元
21、(Ⅰ)证明:在正三棱柱中,平面,则
又是以为直角顶点的等腰直角三角形
则,且
故平面,即:
又为正三角形,所以为的中点
(Ⅱ)解:在正中,取的中点为,则
又平面,则,且
故平面
取的中点为,且的中点为,则
故平面,即:,
在等腰直角中,取的中点为,则,且
所以平面,即
故为二面角的平面角
又
则,
所以在中,,即:
故二面角的大小为
22、解:(Ⅰ)设圆的圆心为,半径为,
则,解得:
故圆的方程为
(Ⅱ)(i)设,,则(*)
由知:
则,即:
将其代入(*)得:
即,此为的轨迹的方程
其轨迹形状为以为圆心,为半径的圆
(ii)假设存在定点满足条件
由在直线上知:可设的坐标为,
设上任意一点的坐标为,则
即:
令,则
即:
则
整理得:
令,即:,且
解得:,
故存在定点使得为常数
数学(理科)
1、本试卷包括第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共4页。全卷满分150分,考试时间120分钟。
2、答第Ⅰ卷时,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号;答第Ⅱ卷时,用0.5毫米的黑色签字笔在答题卡规定的区域内作答,字体工整,笔记清楚;不能答在试题卷上。
3、考试结束后,监考人将答题卡收回。
第Ⅰ卷(选择题,共60分)
一、选择题:本大题共12个小题,每小题5分,共60分,每小题有且只有一个正确答案.
1、已知点,点关于原点的对称点为,则
(A) (B) (C) (D)
2、某学校进行新课程改革实验,为了了解名学生对该项新课程改革实验的意见,打算从中抽取一个容量为的样本,采用系统抽烟方法,则分段的间隔为
(A) (B) (C) (D)
3、上海世博会期间,某日时至时累计入园人数的折线图如图所示,那么在时~时,时~时,...,时~时八个时段中,入园人数最多的时段是
(A)时~时 (B)时~时 (C)时~时 (D)时~时
4、某四面体的三视图如图所示,该四面体的面积为
(A) (B) (C) (D)
5、下列四种说法中,正确说法的个数为
①如果两个平面有三个公共点,那么这两个平面重合;
②两条直线可以确定一个平面;
③若,,,则;
④空间中,两两相交的三条直线在同一个平面内
(A) (B) (C) (D)
6、如图,将边长为的正方形折成一个正四棱柱的侧面,则异面
直线和所成角的大小为
(A) (B)
(C) (D)
7、从编号分别为,,,,的五个大小完全相同的小球中,随机取出三个小球,则恰有两个小球编号相邻的概率为
(A) (B) (C) (D)
8、已知实数,满足,则的最大值为
(A) (B) (C) (D)
9、几何学史上有一个著名的米勒问题:“设点、是锐角的一边上的两点,试在边上找一点,使得最大的.”如图,其结论是:点为过、两点且和射线相切的圆的切点.根据以上结论解决一下问题:在平面直角坐标系中,给定两点,,点在轴上移动,当取最大值时,点的横坐标是
(A)
(B)
(C)或
(D)或
10、已知点,,直线:与线段相交,则实数的取值范围是
(A)或 (B)或 (C) (D)
11、在正方体中,为棱上一点,且,若二面角为,则四面体的外接球的表面积为
(A) (B)
(C) (D)
12、已知圆:,点是直线:上的动点,过点引圆的两条切线、,其中、为切点,则直线经过定点
(A) (B) (C) (D)
第Ⅱ卷(非选择题,共90分)
二、填空题:本大题共4个小题,每小题5分,共20分.
13、已知茎叶图记录了甲、乙两组各名学生在一次英语听力测试中的成绩(单位:分).已知甲组数据的中位数为,乙组数据的平均数为,则的值为 .
甲组 乙组
14、过圆内的点作一条直线,使它被该圆截得的线段最短,则直线的方程是 .
15、秦九韶出生于普州(今资阳市安岳县),是我国南宋时期伟大的数学家,他创立的秦九韶算法历来为人称道,其本质是将一个次多项式写成个一次式相组合的形式,如可将写成,由此可得 .
16、正四棱柱中,,,点为底面四边形的中心,点在侧面四边形的边界及其内部运动,若,则线段长度的最大值为 .
三、解答题:共70分,解答题应写出必要的文字说明、证明过程或演算步骤.
17、(本小题满分10分)
有人参加了某次垃圾分类知识竞赛,从中随机抽取人,将这人的此次竞赛的分数分成组:,,,,,并整理得到如下频率分布直方图,
(Ⅰ)求图中的值;
(Ⅱ)估计总体中竞赛分数不少于分的人数;
(Ⅲ)假设同组中的每个数据都用该组区间的中点值代替,
估计总体人的竞赛分数的平均分.
18、(本小题满分12分)
如图,在直三棱柱中,,,与交于点,为的中点,
(Ⅰ)求证:平面;
(Ⅱ)求证:平面平面.
19、(本小题满分12分)
已知直线过坐标原点,圆的方程为,
(Ⅰ)当直线的斜率为时,求与圆相交所得的弦长;
(Ⅱ)设直线与圆交于两点、,且为的中点,求直线的方程.
20、(本小题满分12分)
年月日,四川汇宇制药股份有限公司在上海证券交易所科创板鸣锣上市,位于内江市经开区的汇宇制药是我省第一家成都市以外的科创板上市企业,也是我省第五家在科创板上市的医药企业.制药设备在使用的过程中,某种机械设备随着使用年限的增加,它的使用功能逐渐减退,使用价值逐年减少,通常把它使用价值逐年减少的“量”换算成费用,称之为“失效费”.某种机械设备的使用年限(单位:年)与失效费(单位:万元)的统计数据如下表所示:
使用年限(单位:年)
失效费(单位:万元)
(Ⅰ)由上表数据可知,可用线性回归模型拟合与的关系.请用相关系数加以说明(精确到);
(Ⅱ)求出关于的线性回归方程,并估算该种机械设备使用年的失效费.
参考公式:,,.
参考数据:,,.
21、(本小题满分12分)
已知正三棱柱底面边长为,是上一点,是以为
直角顶点的等腰直角三角形,
(Ⅰ)证明:是的中点;
(Ⅱ)求二面角的大小.
22、(本小题满分12分)
已知圆的圆心在直线上,与轴正半轴相切,且被直线:截得的弦长为,
(Ⅰ)求圆的方程;
(Ⅱ)设点在圆上运动,点,且点满足,记点的轨迹为,
(i)求的方程,并说明是什么图形;
(ii)试探究:在直线上是否存在定点(异于原点),使得对于上任意一点,都有为一常数,若存在,求出所有满足条件的点的坐标,若不存在,请说明理由.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 C B B A A D C A C B C D
二、填空题
13、 14、 15、 16、
三、解答题
17、解:(Ⅰ)由图知:
解得:
(Ⅱ)样本中,,的频率分布为,,
即:样本中分数不少于分的频率为
则估计总体中不少于分的频率为
故估计总体中不少于分的人数为人
(Ⅲ)样本中平均分的估计值为
故估计总体中的平均分为分
18、解:(Ⅰ)在直三棱柱中,
且四边形为平行四边形,又
则为的中点,又为的中点
故,即:,且平面,平面
所以平面
(Ⅱ)在直三棱柱中,平面
则,且,
故平面,即:
又在平行四边形中,
则四边形为菱形,即:,且
故平面,即:平面平面
19、解:(Ⅰ)由题意知:的方程为,即:
圆的方程可化为:,其圆心为,半径为
则到的距离为
故所求弦长为
(Ⅱ)设,,由为的中点知:,
当斜率不存在时,:
联立,则
故,且,得:方程组无解,此时不符合
当斜率存在时,:
联立,则
故,且,解得:
即:为
综上,所求的方程为
(第(Ⅱ)中,可设的方程为,不用讨论)
20、解:(Ⅰ)由表知:
则
故
所以的值非常接近于,即:可用线性回归模型拟合与的关系
(Ⅱ)由表知:
则,
故所求回归方程为
令,则(万元)
所以估计该设备使用年的失效费为万元
21、(Ⅰ)证明:在正三棱柱中,平面,则
又是以为直角顶点的等腰直角三角形
则,且
故平面,即:
又为正三角形,所以为的中点
(Ⅱ)解:在正中,取的中点为,则
又平面,则,且
故平面
取的中点为,且的中点为,则
故平面,即:,
在等腰直角中,取的中点为,则,且
所以平面,即
故为二面角的平面角
又
则,
所以在中,,即:
故二面角的大小为
22、解:(Ⅰ)设圆的圆心为,半径为,
则,解得:
故圆的方程为
(Ⅱ)(i)设,,则(*)
由知:
则,即:
将其代入(*)得:
即,此为的轨迹的方程
其轨迹形状为以为圆心,为半径的圆
(ii)假设存在定点满足条件
由在直线上知:可设的坐标为,
设上任意一点的坐标为,则
即:
令,则
即:
则
整理得:
令,即:,且
解得:,
故存在定点使得为常数
同课章节目录
