安徽省蚌埠经开区新城实验学校2021-2022学年九年级上期末预测数学试卷(WORD版含答案)
文档属性
| 名称 | 安徽省蚌埠经开区新城实验学校2021-2022学年九年级上期末预测数学试卷(WORD版含答案) | 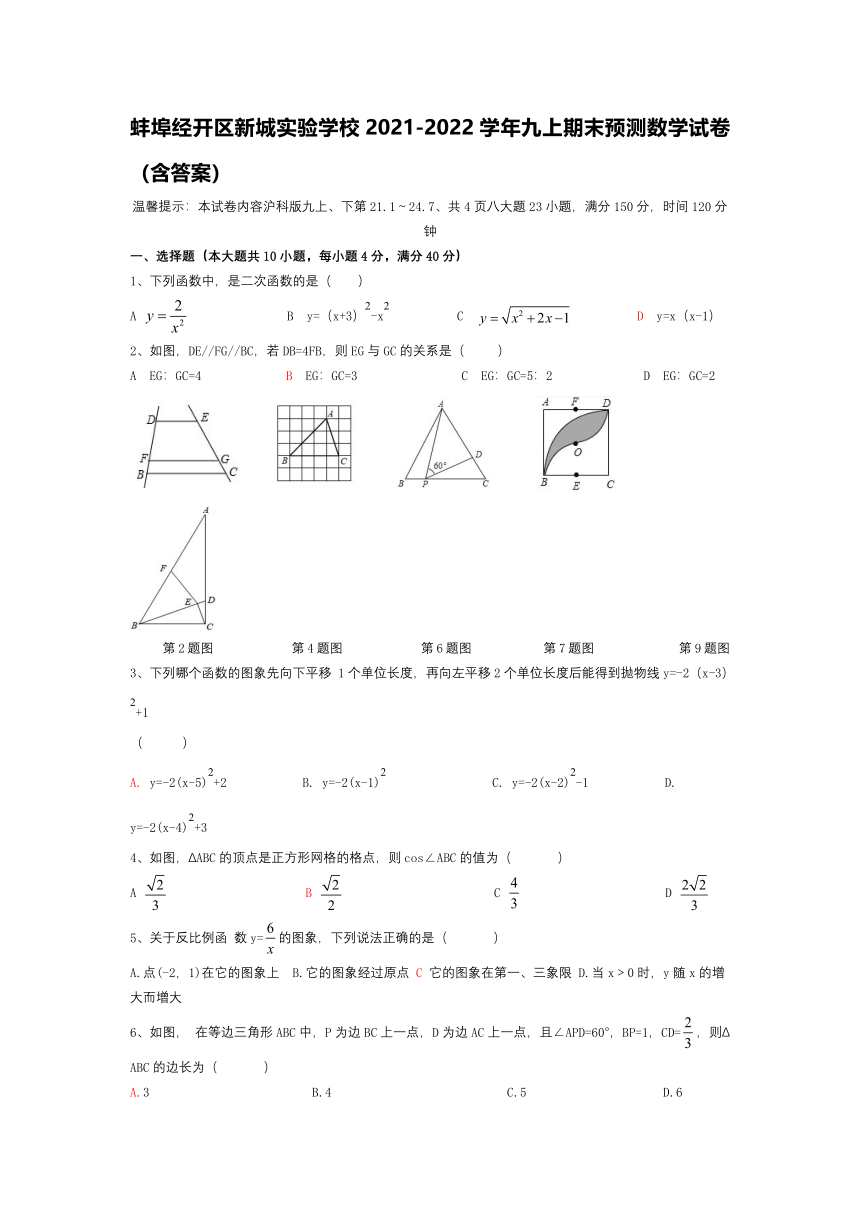 | |
| 格式 | zip | ||
| 文件大小 | 200.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-18 21:00:06 | ||
图片预览



文档简介
蚌埠经开区新城实验学校2021-2022学年九上期末预测数学试卷(含答案)
温馨提示:本试卷内容沪科版九上、下第21.1~24.7、共4页八大题23小题,满分150分,时间120分钟
一、选择题(本大题共10小题,每小题4分,满分40分)
1、下列函数中,是二次函数的是( )
A B y=(x+3)-x C D y=x(x-1)
2、如图,DE//FG//BC,若DB=4FB,则EG与GC的关系是( )
A EG:GC=4 B EG:GC=3 C EG:GC=5:2 D EG:GC=2
第2题图 第4题图 第6题图 第7题图 第9题图
3、下列哪个函数的图象先向下平移 1个单位长度,再向左平移2个单位长度后能得到抛物线y=-2(x-3)+1
( )
A. y=-2(x-5)+2 B. y=-2(x-1) C. y=-2(x-2)-1 D. y=-2(x-4)+3
4、如图,ΔABC的顶点是正方形网格的格点,则cos∠ABC的值为( )
A B C D
5、关于反比例函 数y=的图象,下列说法正确的是( )
A.点(-2,1)在它的图象上 B.它的图象经过原点 C 它的图象在第一、三象限 D.当x>0时,y随x的增大而增大
6、如图, 在等边三角形ABC中,P为边BC上一点,D为边AC上一点,且∠APD=60°,BP=1,CD=,则ΔABC的边长为( )
A.3 B.4 C.5 D.6
7、如图,正方形ABCD的边长为2,0为对角线的交点,点E、F分别为BC/AD的中点,以C为圆心,2为半径作弧BD,再分别以E、F为圆心,1为半径作弧BO、弧OD,则图中阴影部分的面积为( )
A. π-1 B. π-2 C. π-3 D.4
8、若关于x的二次函数y=mx+(m+2)x+m+1的图象与x轴只有一个交点,则m的值为( )
A.0 B.0或2 C.2或-2 D.0或2或-2
9、如图, 在RtΔABC中,∠ACB=90°,∠A=30°,BC=2,D为AC上任一点F为AB中,点,连接BD,E在BD上,且满足CD=DE BD,连接EF,则EF的最小值为( )
A -1 B 1 C D
10、如图,在平面直角坐标系中,点A(2,0)、点B(0,2)、点C(-3,),点P从点0出发沿0→A→B路线以每秒1个单位的速度运动,点Q从点0出发沿0→C→B路线以每秒个单位的速度运动,当一个点到达终点时另个点随之停止运动,设y=PQ,运动时间为秒,则正确表达y与t的关系图象是( )
A B C D
二、填空题(本大题共4小题,每小题5分,满分20分)
11、已知点P是线段AB的黄金分割点,AP>BP,AB=4,那么AP=
12、如图,在平面直角坐标系中,点0为坐标原点,点P在第一象限,⊙P过原点,且与x轴、y轴交于点A、B,
点A的坐标为(6,0),⊙P的直径为,则点B的坐标为
第12题图 第13题图 第14题图
13、如图,点A在反比例承数y=上,点B在x轴上,连接AB交y轴于点E,将AB沿x轴向右平移至CD,其中点C在x轴上,点D在y转上,连接CE,若ΔCDE的面积为3,则k的值为___ .
14、已知四边形ABCD是矩形, AB=2,BC=4,E为BC边上动点且不与B、C重合,连接AE,如图,过点E作EN⊥AB交CD于点N,
①若BE=1,那么CN的长 ; ②2将ΔECN沿EN翻折,点C恰好幕在边AD上,那么BE的长
三、(本大题共2小题,每小题8分,总计16分)
15、计算:4cos30°-3tan60°+2sin45° cos45°
16、已知,求:(1) ; (2)如果2x+y-3z=10,求x的值;
四、(本大题共2小题,每小题8分,总计16分)
17、已知二次函数y=x+bx+c的图像过点A(1,0)、B(0,-3)。求二次函数的解析式和顶点坐标。
18、如图,在平面直角坐标系中,ΔABC的三个顶点的坐标分别是A(1,3)、B(4,1)、C(1,1)
(1)画出与ΔABC关于x轴成轴对称的ΔA1B1C1;
(2)花簇以点O为位似中心,与ΔABC的相似比为2:1的ΔA2B2C2;
五、(本大题共2小题,每小题10分,总计20分)
19、如图,一次函数y=kx+b与反比例函数的图像交于A(m,4)、B(2,n)两点,与坐标轴分别交于M、N两点。
(1)求一次函数的关系式;
(2)根据图像直接写出kx+b->0中x的取值范围;
(3)求ΔABC的面积;
20、如图,旗杆AB竖立在斜坡CB的顶端,斜坡CB长为65米,坡度为i=12:5,小明从与点C相距115米的点D处向上爬12米到达建筑物DE的顶端点E,在此测得旗杆顶端点A的仰角为39°,求旗杆的高度AB。(参考数据:
sin39° ≈0.63,cos39°≈0.78,tan39°≈0.81)
六、(本大题共1小题,每小题12分,总计12分)
21、如图,在⊙0中,,AB是直径,弦CD⊥AB,垂足为H,E为弧BC上一点,F为弦DC延长线上一点,连接FE并延长,交直径AB的延长线于点G,连接AE交CD于点P,若FE=FP.
(1)求证:FE是⊙0的切线; (2若)⊙0的半径为8,sinF=,求BG的长。
七、(本大题共1小题,每小题12分,总计12分)
22、某工厂用50天时间生产一款新型节能产品,每天生产的该产品被某网店以每件80元的价格全部订购,在生产过程中,由于技术的不断更新,该产品第x天的生产成本y(元/件)与x(天)之间的关系如图所示,第x天该产品的生产量z(件)与x(天)满足关系式z=-2x+120
(1)第40天该厂生产该产晶的利润是__ _元;
(2)设第x天该厂生产该产品的利润为w元.
①w与x之间的两数表达式,并指出第几天的利润最大,最大利润是多少?
②在生产该产品的过程中,当天利润不低于2400元的共有多少天?
八、(本大题共1小题,每小题14分,总计14分)
23、如图,在正方形ABCD中,AB=6,M是对角线BD上的一个动点(0<DM<BD),连接AM,过点M作MN⊥AM交BC于点N.
(1)如图①,求证:MA=MN;
(2)如图②,连接AN,O为AN的中点,MO的延长线交边AB于点P,当时,求AN和PM的长;
(3)如图③,过点N作NH⊥BD于H,当AM=2时,求△HMN的面积.
蚌埠经开区新城实验学校2021-2022学年九上期末预测数学试卷答案
1 2 3 4 5 6 7 8 9 10
D B A B C A B D A B
11、 2-2 12、 (3,2) 13、 -6 14、 (1) ; (2)2或
15、 1-
16、 (1)-1; (2)-4;
17、 y=x+2x-3; 顶点(-1,-4)
18、(1)如图所示; (2)如图所示
19、(1)y=-2x+6; (2)x<0或1<x<2;
20、 约24.9米;
温馨提示:本试卷内容沪科版九上、下第21.1~24.7、共4页八大题23小题,满分150分,时间120分钟
一、选择题(本大题共10小题,每小题4分,满分40分)
1、下列函数中,是二次函数的是( )
A B y=(x+3)-x C D y=x(x-1)
2、如图,DE//FG//BC,若DB=4FB,则EG与GC的关系是( )
A EG:GC=4 B EG:GC=3 C EG:GC=5:2 D EG:GC=2
第2题图 第4题图 第6题图 第7题图 第9题图
3、下列哪个函数的图象先向下平移 1个单位长度,再向左平移2个单位长度后能得到抛物线y=-2(x-3)+1
( )
A. y=-2(x-5)+2 B. y=-2(x-1) C. y=-2(x-2)-1 D. y=-2(x-4)+3
4、如图,ΔABC的顶点是正方形网格的格点,则cos∠ABC的值为( )
A B C D
5、关于反比例函 数y=的图象,下列说法正确的是( )
A.点(-2,1)在它的图象上 B.它的图象经过原点 C 它的图象在第一、三象限 D.当x>0时,y随x的增大而增大
6、如图, 在等边三角形ABC中,P为边BC上一点,D为边AC上一点,且∠APD=60°,BP=1,CD=,则ΔABC的边长为( )
A.3 B.4 C.5 D.6
7、如图,正方形ABCD的边长为2,0为对角线的交点,点E、F分别为BC/AD的中点,以C为圆心,2为半径作弧BD,再分别以E、F为圆心,1为半径作弧BO、弧OD,则图中阴影部分的面积为( )
A. π-1 B. π-2 C. π-3 D.4
8、若关于x的二次函数y=mx+(m+2)x+m+1的图象与x轴只有一个交点,则m的值为( )
A.0 B.0或2 C.2或-2 D.0或2或-2
9、如图, 在RtΔABC中,∠ACB=90°,∠A=30°,BC=2,D为AC上任一点F为AB中,点,连接BD,E在BD上,且满足CD=DE BD,连接EF,则EF的最小值为( )
A -1 B 1 C D
10、如图,在平面直角坐标系中,点A(2,0)、点B(0,2)、点C(-3,),点P从点0出发沿0→A→B路线以每秒1个单位的速度运动,点Q从点0出发沿0→C→B路线以每秒个单位的速度运动,当一个点到达终点时另个点随之停止运动,设y=PQ,运动时间为秒,则正确表达y与t的关系图象是( )
A B C D
二、填空题(本大题共4小题,每小题5分,满分20分)
11、已知点P是线段AB的黄金分割点,AP>BP,AB=4,那么AP=
12、如图,在平面直角坐标系中,点0为坐标原点,点P在第一象限,⊙P过原点,且与x轴、y轴交于点A、B,
点A的坐标为(6,0),⊙P的直径为,则点B的坐标为
第12题图 第13题图 第14题图
13、如图,点A在反比例承数y=上,点B在x轴上,连接AB交y轴于点E,将AB沿x轴向右平移至CD,其中点C在x轴上,点D在y转上,连接CE,若ΔCDE的面积为3,则k的值为___ .
14、已知四边形ABCD是矩形, AB=2,BC=4,E为BC边上动点且不与B、C重合,连接AE,如图,过点E作EN⊥AB交CD于点N,
①若BE=1,那么CN的长 ; ②2将ΔECN沿EN翻折,点C恰好幕在边AD上,那么BE的长
三、(本大题共2小题,每小题8分,总计16分)
15、计算:4cos30°-3tan60°+2sin45° cos45°
16、已知,求:(1) ; (2)如果2x+y-3z=10,求x的值;
四、(本大题共2小题,每小题8分,总计16分)
17、已知二次函数y=x+bx+c的图像过点A(1,0)、B(0,-3)。求二次函数的解析式和顶点坐标。
18、如图,在平面直角坐标系中,ΔABC的三个顶点的坐标分别是A(1,3)、B(4,1)、C(1,1)
(1)画出与ΔABC关于x轴成轴对称的ΔA1B1C1;
(2)花簇以点O为位似中心,与ΔABC的相似比为2:1的ΔA2B2C2;
五、(本大题共2小题,每小题10分,总计20分)
19、如图,一次函数y=kx+b与反比例函数的图像交于A(m,4)、B(2,n)两点,与坐标轴分别交于M、N两点。
(1)求一次函数的关系式;
(2)根据图像直接写出kx+b->0中x的取值范围;
(3)求ΔABC的面积;
20、如图,旗杆AB竖立在斜坡CB的顶端,斜坡CB长为65米,坡度为i=12:5,小明从与点C相距115米的点D处向上爬12米到达建筑物DE的顶端点E,在此测得旗杆顶端点A的仰角为39°,求旗杆的高度AB。(参考数据:
sin39° ≈0.63,cos39°≈0.78,tan39°≈0.81)
六、(本大题共1小题,每小题12分,总计12分)
21、如图,在⊙0中,,AB是直径,弦CD⊥AB,垂足为H,E为弧BC上一点,F为弦DC延长线上一点,连接FE并延长,交直径AB的延长线于点G,连接AE交CD于点P,若FE=FP.
(1)求证:FE是⊙0的切线; (2若)⊙0的半径为8,sinF=,求BG的长。
七、(本大题共1小题,每小题12分,总计12分)
22、某工厂用50天时间生产一款新型节能产品,每天生产的该产品被某网店以每件80元的价格全部订购,在生产过程中,由于技术的不断更新,该产品第x天的生产成本y(元/件)与x(天)之间的关系如图所示,第x天该产品的生产量z(件)与x(天)满足关系式z=-2x+120
(1)第40天该厂生产该产晶的利润是__ _元;
(2)设第x天该厂生产该产品的利润为w元.
①w与x之间的两数表达式,并指出第几天的利润最大,最大利润是多少?
②在生产该产品的过程中,当天利润不低于2400元的共有多少天?
八、(本大题共1小题,每小题14分,总计14分)
23、如图,在正方形ABCD中,AB=6,M是对角线BD上的一个动点(0<DM<BD),连接AM,过点M作MN⊥AM交BC于点N.
(1)如图①,求证:MA=MN;
(2)如图②,连接AN,O为AN的中点,MO的延长线交边AB于点P,当时,求AN和PM的长;
(3)如图③,过点N作NH⊥BD于H,当AM=2时,求△HMN的面积.
蚌埠经开区新城实验学校2021-2022学年九上期末预测数学试卷答案
1 2 3 4 5 6 7 8 9 10
D B A B C A B D A B
11、 2-2 12、 (3,2) 13、 -6 14、 (1) ; (2)2或
15、 1-
16、 (1)-1; (2)-4;
17、 y=x+2x-3; 顶点(-1,-4)
18、(1)如图所示; (2)如图所示
19、(1)y=-2x+6; (2)x<0或1<x<2;
20、 约24.9米;
同课章节目录
