上海市徐汇区2021-2022学年八年级上学期期末考试数学试题(word版,含答案)
文档属性
| 名称 | 上海市徐汇区2021-2022学年八年级上学期期末考试数学试题(word版,含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 259.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-18 00:00:00 | ||
图片预览

文档简介
徐汇区学年初二年级第一学期
期末考试 数学试卷
(考试时间90分钟,满分100分)
选择题(本大题共6题,每题3分,满分18分)
1.下列二次根式中,是最简二次根式的是( )
(A) ; (B) ; (C) ;(D) .
2.下列方程中,没有实数根的是( )
(A) (B)(C) (D)
3.如果正比例函数图像与反比例函数图像的一个交点的坐标为(3,-4),那么另一个交点的坐标为( ).
(A)(-3,-4) (B)(3,4) (C)( 3,4) (D)(-4,3)
4.满足下列条件的三角形中,不是直角三角形的是( )
(A)三内角之比为3:4:5; (B)三边长的平方之比为1:2:3;
(C)三边长之比为7:24:25; (D)三内角之比为1:2:3.
5. 下列命题中,其逆命题是真命题的命题个数有( )
(1)全等三角形的对应边相等; (2)对顶角相等;
(3)等角对等边; (4)全等三角形的面积相等.
(A)1个; (B)2个; (C)3个; (D)4个.
6. 如图所示,在平面直角坐标系xOy中,点A、B、C为反比例函数y= (k>0)上不同的三点,连接OA、OB、OC,过点A作AD⊥y轴于点D,过点B、C分别作BE,CF垂直x轴于点E、F,OC与BE相交于点M,记△AOD、△BOM、四边形CMEF的面积分别为S1、S2、S3,则( )
(A)S1=S2+S3 ; (B)S2=S3;
(C)S3>S2>S1; (D)S1S2<S32.
填空题(本大题共12题,每题2分,满分24分)
7. 函数 y=的定义域为____________.
8. 已知,那么___________.
9.已知0是关于的一元二次方程的一个实数根,则= .
10.在实数范围内因式分解:____________________.
11.若、两点都在函数的图像上,且<,则k的取值范围是 .
12.已知正比例函数的图像经过第一、三象限,且经过点(k,k+2),则k=________.
13.以线段AB为底边的等腰三角形,它的两底角平分线交点的轨迹是 .
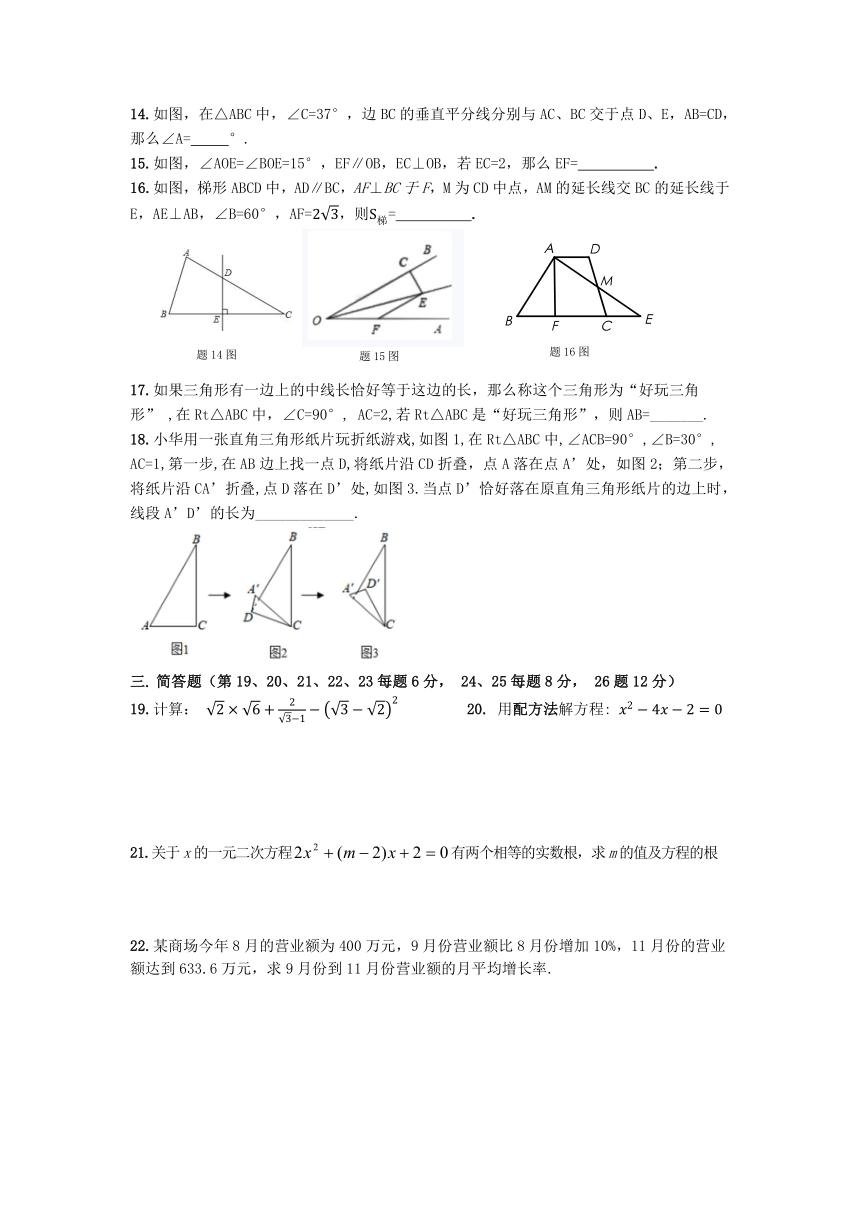
14.如图,在△ABC中,∠C=37°,边BC的垂直平分线分别与AC、BC交于点D、E,AB=CD,那么∠A= °.
15.如图,∠AOE=∠BOE=15°,EF∥OB,EC⊥OB,若EC=2,那么EF= .
16.如图,梯形ABCD中,AD∥BC,AF⊥BC于F,M为CD中点,AM的延长线交BC的延长线于E,AE⊥AB,∠B=60°,AF=,则= .
17.如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形为“好玩三角形” ,在Rt△ABC中,∠C=90°, AC=2,若Rt△ABC是“好玩三角形”,则AB=_______.
18.小华用一张直角三角形纸片玩折纸游戏,如图1,在Rt△ABC中,∠ACB=90°,∠B=30°,
AC=1,第一步,在AB边上找一点D,将纸片沿CD折叠,点A落在点A’处,如图2;第二步,将纸片沿CA’折叠,点D落在D’处,如图3.当点D’恰好落在原直角三角形纸片的边上时,线段A’D’的长为_____________.
简答题(第19、20、21、22、23每题6分, 24、25每题8分, 26题12分)
19.计算: 20. 用配方法解方程:
21.关于x的一元二次方程有两个相等的实数根,求m的值及方程的根
22.某商场今年8月的营业额为400万元,9月份营业额比8月份增加10%,11月份的营业额达到633.6万元,求9月份到11月份营业额的月平均增长率.
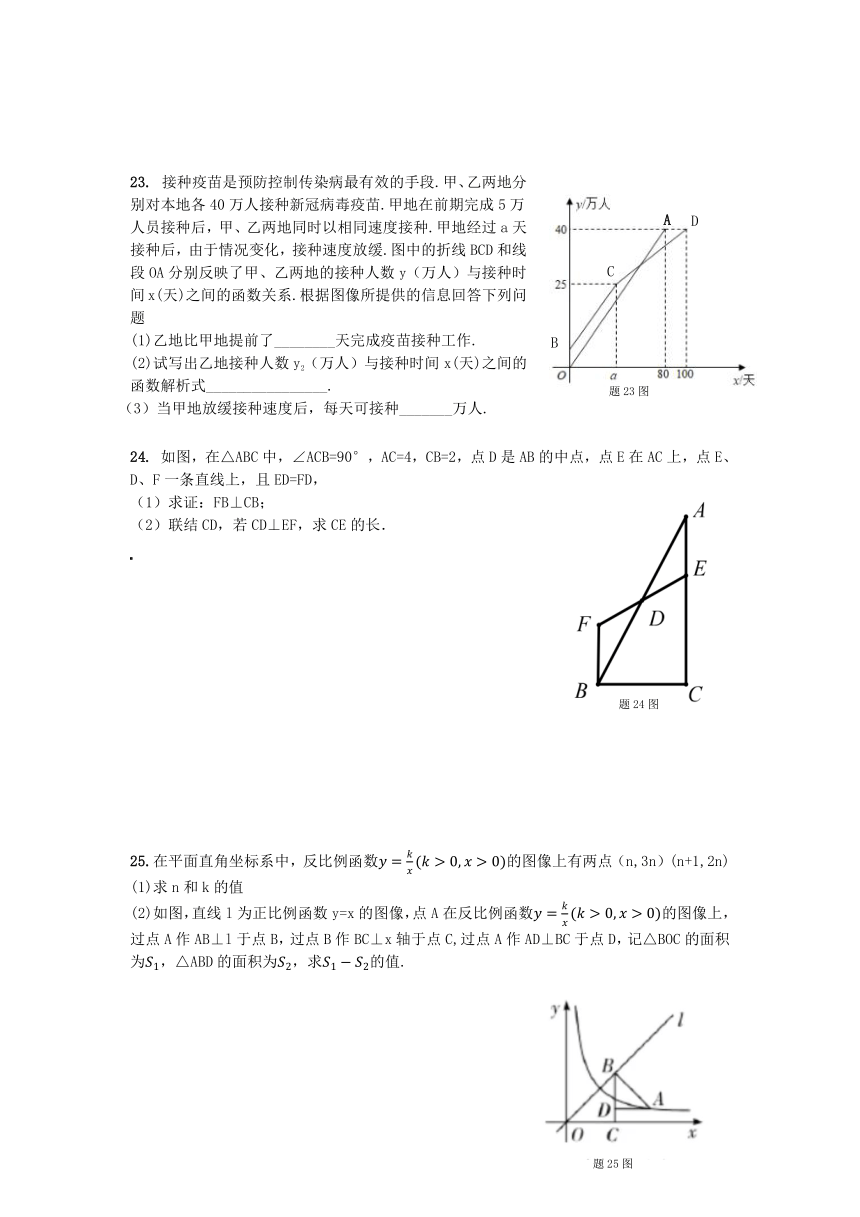
23. 接种疫苗是预防控制传染病最有效的手段.甲、乙两地分别对本地各40万人接种新冠病毒疫苗.甲地在前期完成5万人员接种后,甲、乙两地同时以相同速度接种.甲地经过a天接种后,由于情况变化,接种速度放缓.图中的折线BCD和线段OA分别反映了甲、乙两地的接种人数y(万人)与接种时间x(天)之间的函数关系.根据图像所提供的信息回答下列问题
(1)乙地比甲地提前了________天完成疫苗接种工作.
(2)试写出乙地接种人数y2(万人)与接种时间x(天)之间的函数解析式________________.
(3)当甲地放缓接种速度后,每天可接种_______万人.
24. 如图,在△ABC中,∠ACB=90°,AC=4,CB=2,点D是AB的中点,点E在AC上,点E、D、F一条直线上,且ED=FD,
(1)求证:FB⊥CB;
(2)联结CD,若CD⊥EF,求CE的长.
25.在平面直角坐标系中,反比例函数的图像上有两点(n,3n)(n+1,2n)
(1)求n和k的值
(2)如图,直线l为正比例函数y=x的图像,点A在反比例函数的图像上,过点A作AB⊥l于点B,过点B作BC⊥x轴于点C,过点A作AD⊥BC于点D,记△BOC的面积为,△ABD的面积为,求的值.
26. 如图1所示,已知△ABC中,∠ACB=90°,BC=2,AC=,点D在射线BC上,以点D为圆心,BD为半径画弧交AB边AB于点E,过点E作EF⊥AB交边AC于点F,射线ED交射线AC于点G.
(1)求证:EA=EG;
(2)若点G在线段AC延长线上时,设BD=x,FC=y,求y关于x的函数解析式并写出定义域;
(3)联结DF,当△DFG是等腰三角形时,请直接写出BD的长度.
图1 备用图
徐汇区2021学年初二年级第一学期期末考试评分标准参考
一.选择题:(本大题共6小题,每小题3分,满分18分)
D ; 2.D; 3.C; 4.A; 5.B; 6.B.
二.填空题:(本大题共12小题,每小题2分,满分24分)
7. x≤2 8. -1 10.)
k<0 12. 2 13.线段AB的垂直平分线(AB中点除外) 14. 74
4 16, 18.
三.简答题:(本大题共8小题,满分58分)
19.本题满分6分.
解:原式=2----------------------------(1+2+2分)
=3.----------------------------------------(1分)
本题满分6分.
解:,-----------------------------------------(1分)
,--------------------------------------------(1分)
,--------------------------------------------(1分)
,-----------------------------------------------(1分)
∴原方程的解是,.-------------------------------------(2分)
本题满分6分.
解:-------------------------------------(1分)
∵方程有两个相等的实数根,
∴=0.-----------------------------------(1分)
∴------------------------------------(2分)
当时,--------------------------------------------------(1分)
当时,--------------------------------------------------(1分)
22.本题满分6分.
解:设9月份到11月份营业额的月平均增长率为x.--------------------------(1分)
--------------------(2分)
解得:0.2=20%,-2.2(不符合题意,舍去) ------------(2分)
答:9月份到11月份营业额的月平均增长率为20%.---------------------------(1分)
23.本题共3小题,每空2分,满分6分.
解:(1)20; (2)x; (3)0.25.
本题共2小题,第一题4分,第二题4分,满分8分.
证:(1)∵D是AB中点,∴AD=BD ----------------(1分)
在△ADE与△BDF中,
∴△ADE△BDF
∴,AE=BF. ---------------------------------------------------(1分)
∵∠ACB=90°,∴∠A+∠ABC=90°,------------------------------------------(1分)
∴+∠ABC=90°,即FBC=90°,∴FBCB.------------------------------(1分)
联结CF.
∵CDEF,ED=FD,
∴CF=EF,---------------------------------------------(1分)
设CE=x,则CF=x,BF=AE=4-x,
Rt△FBC中,---------------------------------------------(1分)
∴---------------------------------------(1分)
∴x= ,即CE=.-----------------------------------------------------------(1分)
本题共2小题,第一题4分,第二题4分,满分8分.
解:(1)将(n,3n),(n+1,2n)代入---------------------------------------(1分)
消去k,整理得:-------------------------------------(1分)
解得:(舍),2---------------------------------------------------(1分)
∴k=12------------------------------------------------(1分)
(2)设B(a,a)
∴BC=OC=a,∴∠COB=∠CBO,
∵BCx轴,∴∠BCO=90°,
∴∠COB+∠CBO=90°,∴∠COB=∠CBO=45°.-----------------------------------(1分)
∵AB直线l,∴∠ABO=∠CBO+∠ABD=90°,
∴∠ABD=45°
∵ADBC,∴∠ABD+∠BAD=90°,
∴∠BAD=45°,∴∠BAD=∠ABD,∴DB=DA,------------------------------------(1分)
设DB=DA=t,则A(a+t,a-t)
∵A在反比例函数的图像上,∴(a+t)(a-t)=12---------------------------(1分)
= 6-----------------(1分)
本题共3小题,第一题5分,第二题4分,第三题3分,满分12分.
解:(1)Rt△ACB中,∠C=90°
∴
∵AC=2,BC=2,∴AB=4,------------------------------------(1分)
∴,∴∠A=30°,---------------------------------------------------(1分)
∵∠A+∠B=90°,∴∠B=60°,
∵DE=DB,∴△DEB是等边三角形,-------------------------------------------(1分)
∴∠BED=60°,
∵∠BED=∠A+∠G,
∴∠G=30°----------------------------------------(1分)
∴∠A=∠G,
∴EA=EG.-----------------------------------------------(1分)
∵△DEB是等边三角形,
∴BE=DE
设BE=x,则DE=x,AE=AB-BE=4-x
∵∠A=30°,∠AEF=90°,
∴EF=,
Rt△AEF中,
∴,--------------------------------(2分)
∵FC=AC-AF,
∴= -------------------------(1分)
定义域:1≤x<2---------------------------------------(1分)
(3) -----------------------(3分)
期末考试 数学试卷
(考试时间90分钟,满分100分)
选择题(本大题共6题,每题3分,满分18分)
1.下列二次根式中,是最简二次根式的是( )
(A) ; (B) ; (C) ;(D) .
2.下列方程中,没有实数根的是( )
(A) (B)(C) (D)
3.如果正比例函数图像与反比例函数图像的一个交点的坐标为(3,-4),那么另一个交点的坐标为( ).
(A)(-3,-4) (B)(3,4) (C)( 3,4) (D)(-4,3)
4.满足下列条件的三角形中,不是直角三角形的是( )
(A)三内角之比为3:4:5; (B)三边长的平方之比为1:2:3;
(C)三边长之比为7:24:25; (D)三内角之比为1:2:3.
5. 下列命题中,其逆命题是真命题的命题个数有( )
(1)全等三角形的对应边相等; (2)对顶角相等;
(3)等角对等边; (4)全等三角形的面积相等.
(A)1个; (B)2个; (C)3个; (D)4个.
6. 如图所示,在平面直角坐标系xOy中,点A、B、C为反比例函数y= (k>0)上不同的三点,连接OA、OB、OC,过点A作AD⊥y轴于点D,过点B、C分别作BE,CF垂直x轴于点E、F,OC与BE相交于点M,记△AOD、△BOM、四边形CMEF的面积分别为S1、S2、S3,则( )
(A)S1=S2+S3 ; (B)S2=S3;
(C)S3>S2>S1; (D)S1S2<S32.
填空题(本大题共12题,每题2分,满分24分)
7. 函数 y=的定义域为____________.
8. 已知,那么___________.
9.已知0是关于的一元二次方程的一个实数根,则= .
10.在实数范围内因式分解:____________________.
11.若、两点都在函数的图像上,且<,则k的取值范围是 .
12.已知正比例函数的图像经过第一、三象限,且经过点(k,k+2),则k=________.
13.以线段AB为底边的等腰三角形,它的两底角平分线交点的轨迹是 .
14.如图,在△ABC中,∠C=37°,边BC的垂直平分线分别与AC、BC交于点D、E,AB=CD,那么∠A= °.
15.如图,∠AOE=∠BOE=15°,EF∥OB,EC⊥OB,若EC=2,那么EF= .
16.如图,梯形ABCD中,AD∥BC,AF⊥BC于F,M为CD中点,AM的延长线交BC的延长线于E,AE⊥AB,∠B=60°,AF=,则= .
17.如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形为“好玩三角形” ,在Rt△ABC中,∠C=90°, AC=2,若Rt△ABC是“好玩三角形”,则AB=_______.
18.小华用一张直角三角形纸片玩折纸游戏,如图1,在Rt△ABC中,∠ACB=90°,∠B=30°,
AC=1,第一步,在AB边上找一点D,将纸片沿CD折叠,点A落在点A’处,如图2;第二步,将纸片沿CA’折叠,点D落在D’处,如图3.当点D’恰好落在原直角三角形纸片的边上时,线段A’D’的长为_____________.
简答题(第19、20、21、22、23每题6分, 24、25每题8分, 26题12分)
19.计算: 20. 用配方法解方程:
21.关于x的一元二次方程有两个相等的实数根,求m的值及方程的根
22.某商场今年8月的营业额为400万元,9月份营业额比8月份增加10%,11月份的营业额达到633.6万元,求9月份到11月份营业额的月平均增长率.
23. 接种疫苗是预防控制传染病最有效的手段.甲、乙两地分别对本地各40万人接种新冠病毒疫苗.甲地在前期完成5万人员接种后,甲、乙两地同时以相同速度接种.甲地经过a天接种后,由于情况变化,接种速度放缓.图中的折线BCD和线段OA分别反映了甲、乙两地的接种人数y(万人)与接种时间x(天)之间的函数关系.根据图像所提供的信息回答下列问题
(1)乙地比甲地提前了________天完成疫苗接种工作.
(2)试写出乙地接种人数y2(万人)与接种时间x(天)之间的函数解析式________________.
(3)当甲地放缓接种速度后,每天可接种_______万人.
24. 如图,在△ABC中,∠ACB=90°,AC=4,CB=2,点D是AB的中点,点E在AC上,点E、D、F一条直线上,且ED=FD,
(1)求证:FB⊥CB;
(2)联结CD,若CD⊥EF,求CE的长.
25.在平面直角坐标系中,反比例函数的图像上有两点(n,3n)(n+1,2n)
(1)求n和k的值
(2)如图,直线l为正比例函数y=x的图像,点A在反比例函数的图像上,过点A作AB⊥l于点B,过点B作BC⊥x轴于点C,过点A作AD⊥BC于点D,记△BOC的面积为,△ABD的面积为,求的值.
26. 如图1所示,已知△ABC中,∠ACB=90°,BC=2,AC=,点D在射线BC上,以点D为圆心,BD为半径画弧交AB边AB于点E,过点E作EF⊥AB交边AC于点F,射线ED交射线AC于点G.
(1)求证:EA=EG;
(2)若点G在线段AC延长线上时,设BD=x,FC=y,求y关于x的函数解析式并写出定义域;
(3)联结DF,当△DFG是等腰三角形时,请直接写出BD的长度.
图1 备用图
徐汇区2021学年初二年级第一学期期末考试评分标准参考
一.选择题:(本大题共6小题,每小题3分,满分18分)
D ; 2.D; 3.C; 4.A; 5.B; 6.B.
二.填空题:(本大题共12小题,每小题2分,满分24分)
7. x≤2 8. -1 10.)
k<0 12. 2 13.线段AB的垂直平分线(AB中点除外) 14. 74
4 16, 18.
三.简答题:(本大题共8小题,满分58分)
19.本题满分6分.
解:原式=2----------------------------(1+2+2分)
=3.----------------------------------------(1分)
本题满分6分.
解:,-----------------------------------------(1分)
,--------------------------------------------(1分)
,--------------------------------------------(1分)
,-----------------------------------------------(1分)
∴原方程的解是,.-------------------------------------(2分)
本题满分6分.
解:-------------------------------------(1分)
∵方程有两个相等的实数根,
∴=0.-----------------------------------(1分)
∴------------------------------------(2分)
当时,--------------------------------------------------(1分)
当时,--------------------------------------------------(1分)
22.本题满分6分.
解:设9月份到11月份营业额的月平均增长率为x.--------------------------(1分)
--------------------(2分)
解得:0.2=20%,-2.2(不符合题意,舍去) ------------(2分)
答:9月份到11月份营业额的月平均增长率为20%.---------------------------(1分)
23.本题共3小题,每空2分,满分6分.
解:(1)20; (2)x; (3)0.25.
本题共2小题,第一题4分,第二题4分,满分8分.
证:(1)∵D是AB中点,∴AD=BD ----------------(1分)
在△ADE与△BDF中,
∴△ADE△BDF
∴,AE=BF. ---------------------------------------------------(1分)
∵∠ACB=90°,∴∠A+∠ABC=90°,------------------------------------------(1分)
∴+∠ABC=90°,即FBC=90°,∴FBCB.------------------------------(1分)
联结CF.
∵CDEF,ED=FD,
∴CF=EF,---------------------------------------------(1分)
设CE=x,则CF=x,BF=AE=4-x,
Rt△FBC中,---------------------------------------------(1分)
∴---------------------------------------(1分)
∴x= ,即CE=.-----------------------------------------------------------(1分)
本题共2小题,第一题4分,第二题4分,满分8分.
解:(1)将(n,3n),(n+1,2n)代入---------------------------------------(1分)
消去k,整理得:-------------------------------------(1分)
解得:(舍),2---------------------------------------------------(1分)
∴k=12------------------------------------------------(1分)
(2)设B(a,a)
∴BC=OC=a,∴∠COB=∠CBO,
∵BCx轴,∴∠BCO=90°,
∴∠COB+∠CBO=90°,∴∠COB=∠CBO=45°.-----------------------------------(1分)
∵AB直线l,∴∠ABO=∠CBO+∠ABD=90°,
∴∠ABD=45°
∵ADBC,∴∠ABD+∠BAD=90°,
∴∠BAD=45°,∴∠BAD=∠ABD,∴DB=DA,------------------------------------(1分)
设DB=DA=t,则A(a+t,a-t)
∵A在反比例函数的图像上,∴(a+t)(a-t)=12---------------------------(1分)
= 6-----------------(1分)
本题共3小题,第一题5分,第二题4分,第三题3分,满分12分.
解:(1)Rt△ACB中,∠C=90°
∴
∵AC=2,BC=2,∴AB=4,------------------------------------(1分)
∴,∴∠A=30°,---------------------------------------------------(1分)
∵∠A+∠B=90°,∴∠B=60°,
∵DE=DB,∴△DEB是等边三角形,-------------------------------------------(1分)
∴∠BED=60°,
∵∠BED=∠A+∠G,
∴∠G=30°----------------------------------------(1分)
∴∠A=∠G,
∴EA=EG.-----------------------------------------------(1分)
∵△DEB是等边三角形,
∴BE=DE
设BE=x,则DE=x,AE=AB-BE=4-x
∵∠A=30°,∠AEF=90°,
∴EF=,
Rt△AEF中,
∴,--------------------------------(2分)
∵FC=AC-AF,
∴= -------------------------(1分)
定义域:1≤x<2---------------------------------------(1分)
(3) -----------------------(3分)
同课章节目录
