2021-2022学年北师大版数学八年级下册第1章三角形的证明复习(二)教案
文档属性
| 名称 | 2021-2022学年北师大版数学八年级下册第1章三角形的证明复习(二)教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 145.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-18 00:00:00 | ||
图片预览

文档简介
第1章 三角形的证明复习(二)
一、复习目标
1.在回顾与思考中建立本章的知识框架图,复习有关定理的探索与证明,证明的思路和方法,尺规作图等.
2.进一步体会证明的必要性,发展学生的初步的演绎推理能力;进一步掌握综合法的证明方法,结合实例体会反证法的含义;提高学生用规范的数学语言表达论证过程的能力.
二、课时安排
1课时
三、复习重难点
重点:线段垂直平分线与角平分线的性质和判定.
难点:线段垂直平分线与角平分线的综合应用.
四、教学过程
(一)知识梳理
1.直角三角形的性质
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的 .
2.勾股定理及其逆定理
勾股定理:直角三角形两条直角边的平方和等于斜边的 .
逆定理:如果三角形两边的平方和等于第三边的平方,那么这个三角形是 三角形
3.线段的垂直平分线的性质定理及判定定理
性质定理:线段的垂直平分线上的点到这条线段两个端点的距离 .
判定定理:到一条线段两个端点距离相等的点,在这条线段
的 上.
4.三线共点
三角形三条边的垂直平分线相交于 ,并且这一点到三角形三个顶点的距离 .
5.角平分线的性质定理及判定定理
性质定理:角平分线上的点到这个角两边的距离 .
判定定理:在一个角的内部,且到角的两边 相等的点,在这个角的平分线上.
[注意] 角的平分线是在角的内部的一条射线,所以它的逆定理必须加上“在角的内部”这个条件.
6.三角形三条角平分线的性质
三角形的三条角平分线相交于一点,并且这一点到三条边的距离 .
(二)题型、技巧归纳
考点一 勾股定理及逆定理的应用
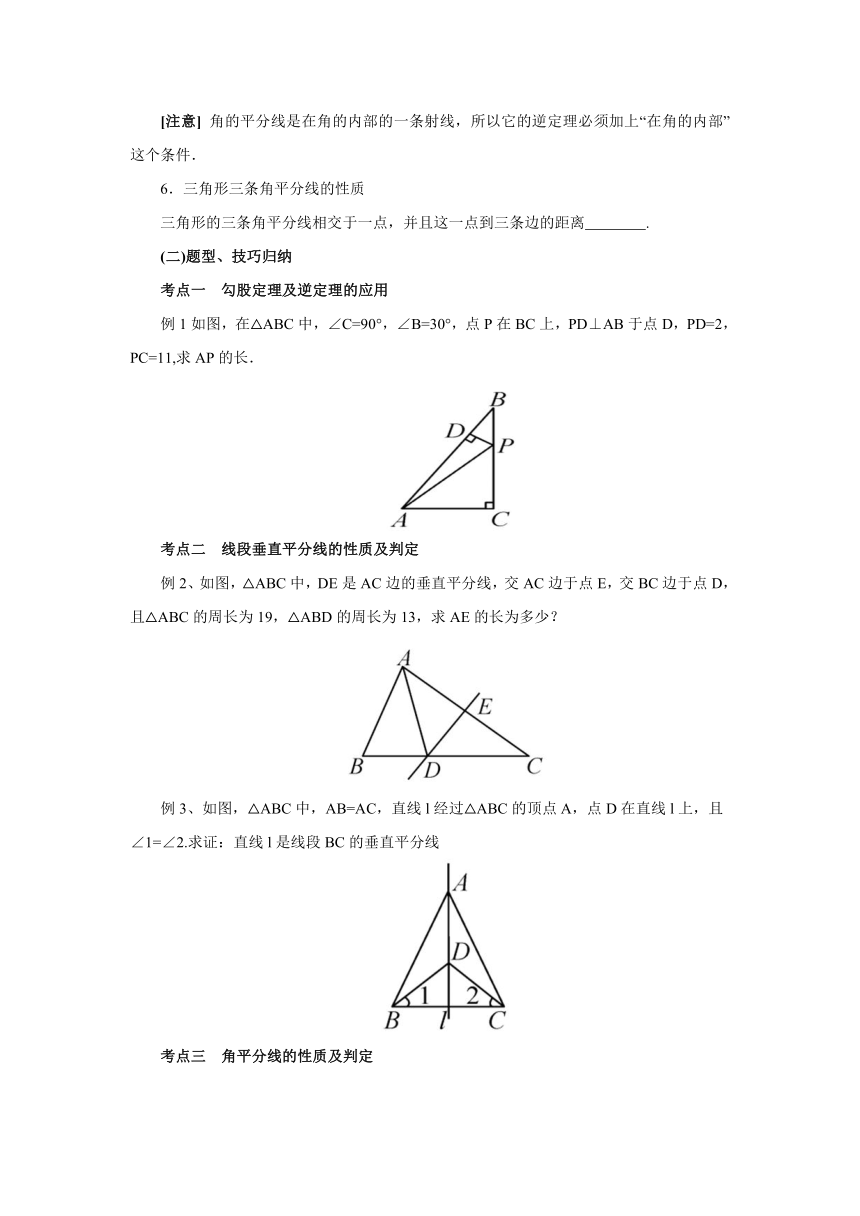
如图,在△ABC中,∠C=90°,∠B=30°,点P在BC上,PD⊥AB于点D,PD=2,PC=11,求AP的长.
考点二 线段垂直平分线的性质及判定
例2、如图,△ABC中,DE是AC边的垂直平分线,交AC边于点E,交BC边于点D,且△ABC的周长为19,△ABD的周长为13,求AE的长为多少?
例3、如图,△ABC中,AB=AC,直线l经过△ABC的顶点A,点D在直线l上,且∠1=∠2.求证:直线l是线段BC的垂直平分线
考点三 角平分线的性质及判定
例4、如图,已知∠1=∠2,P为BN上一点且PD⊥BC于D,AB+BC=2BD,求证:∠BAP+∠BCP=180°
例5、如图,CE⊥AB于E,BF⊥AC于F,BF于CE交于点D,BE=CF.
求证:AD平分∠BAC
典例精讲
1.下列命题中,是真命题的是 ( )
A.相等的角是对顶角 B.两直线平行,同位角互补
C.等腰三角形的两个底角相等 D.直角三角形中两锐角互补
2.若三角形三边长之比为1∶∶2,则这个三角形中的最大角的度数是 ( )
A.60° B.90° C.120° D.150°
3.在△ABC中,若∠A∶∠B∶∠C=3∶1∶2,则其各角所对边长之比等于 ( )
A.∶1∶2 B.1∶2∶ C.1∶∶2 D.2∶1∶
4.到线段AB两个端点距离相等的点,在 .
5.直角三角形ABC中,∠C=90°,AC的垂直平分线交AB于D,若AD=2 cm,则BD= cm.
6.如图1-80所示,△ABC中,AB,AC的垂直平分线分别交BC于点D,E,已知△ADE的周长为12 cm,求BC的长.
7.如图1-81所示,A,B是公路l(l为东西走向)两旁的两个村庄,A村到公路l的距离AC=1 km,B村到公路l的距离BD=2 km,B村在A村的南偏东45°方向上.
(1)求A,B两村之间的距离;
(2)为方便村民出行,计划在公路边新建一个公共汽车站P,要求该站到两村的距离相等,请用尺规在图中作出点P的位置.(保留清晰的作图痕迹,并简要写明作法)
(四)归纳小结
1.本节课学习了哪些主要内容?
2.勾股定理,垂直平分线以及角平分线的性质与判定的应用。
3.在应用时要注意哪些问题?
随堂检测
1.如图,△ABC中,∠ACB=90°,BA的垂直平分线交CB边于D,若AB=10,AC=5,则图中等于60°的角的个数为( )
A.2 B.3 C.4 D.5
2.如图,在Rt△ABC中,∠C=90°,∠B=15°,DE是AB的中垂线,垂足为D,交BC于点E,若BE=4,则AC=________.
3.若点P是△ABC内一点,PD⊥AB于D,PE⊥BC于E,PF⊥AC于F,且PD=PE=PF,则点P是△ABC的( )
A.三条高的交点 B.三条中线的交点
C.三条角平分线的交点 D.三条中垂线的交点
4.在平面内,到A,B,C三点距离相等的点有( )
A.只有一个 B.有两个
C.有三个或三个以上 D.有一个或没有
5.如图,在四边形ABCD中,AD∥BC,E为CD的中点,连结AE,BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)FC=AD;
(2)AB=BC+AD.
6、在ΔABC中,∠C=900,∠B=300,AD是∠BAC的平分线,已知AB= ,求AD的长.
五、板书设计
把黑板分成两份,左边部分板书例题,右边部分板书学习练习题,重复使用
六、作业布置
完成课后同步练习题
一、复习目标
1.在回顾与思考中建立本章的知识框架图,复习有关定理的探索与证明,证明的思路和方法,尺规作图等.
2.进一步体会证明的必要性,发展学生的初步的演绎推理能力;进一步掌握综合法的证明方法,结合实例体会反证法的含义;提高学生用规范的数学语言表达论证过程的能力.
二、课时安排
1课时
三、复习重难点
重点:线段垂直平分线与角平分线的性质和判定.
难点:线段垂直平分线与角平分线的综合应用.
四、教学过程
(一)知识梳理
1.直角三角形的性质
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的 .
2.勾股定理及其逆定理
勾股定理:直角三角形两条直角边的平方和等于斜边的 .
逆定理:如果三角形两边的平方和等于第三边的平方,那么这个三角形是 三角形
3.线段的垂直平分线的性质定理及判定定理
性质定理:线段的垂直平分线上的点到这条线段两个端点的距离 .
判定定理:到一条线段两个端点距离相等的点,在这条线段
的 上.
4.三线共点
三角形三条边的垂直平分线相交于 ,并且这一点到三角形三个顶点的距离 .
5.角平分线的性质定理及判定定理
性质定理:角平分线上的点到这个角两边的距离 .
判定定理:在一个角的内部,且到角的两边 相等的点,在这个角的平分线上.
[注意] 角的平分线是在角的内部的一条射线,所以它的逆定理必须加上“在角的内部”这个条件.
6.三角形三条角平分线的性质
三角形的三条角平分线相交于一点,并且这一点到三条边的距离 .
(二)题型、技巧归纳
考点一 勾股定理及逆定理的应用
如图,在△ABC中,∠C=90°,∠B=30°,点P在BC上,PD⊥AB于点D,PD=2,PC=11,求AP的长.
考点二 线段垂直平分线的性质及判定
例2、如图,△ABC中,DE是AC边的垂直平分线,交AC边于点E,交BC边于点D,且△ABC的周长为19,△ABD的周长为13,求AE的长为多少?
例3、如图,△ABC中,AB=AC,直线l经过△ABC的顶点A,点D在直线l上,且∠1=∠2.求证:直线l是线段BC的垂直平分线
考点三 角平分线的性质及判定
例4、如图,已知∠1=∠2,P为BN上一点且PD⊥BC于D,AB+BC=2BD,求证:∠BAP+∠BCP=180°
例5、如图,CE⊥AB于E,BF⊥AC于F,BF于CE交于点D,BE=CF.
求证:AD平分∠BAC
典例精讲
1.下列命题中,是真命题的是 ( )
A.相等的角是对顶角 B.两直线平行,同位角互补
C.等腰三角形的两个底角相等 D.直角三角形中两锐角互补
2.若三角形三边长之比为1∶∶2,则这个三角形中的最大角的度数是 ( )
A.60° B.90° C.120° D.150°
3.在△ABC中,若∠A∶∠B∶∠C=3∶1∶2,则其各角所对边长之比等于 ( )
A.∶1∶2 B.1∶2∶ C.1∶∶2 D.2∶1∶
4.到线段AB两个端点距离相等的点,在 .
5.直角三角形ABC中,∠C=90°,AC的垂直平分线交AB于D,若AD=2 cm,则BD= cm.
6.如图1-80所示,△ABC中,AB,AC的垂直平分线分别交BC于点D,E,已知△ADE的周长为12 cm,求BC的长.
7.如图1-81所示,A,B是公路l(l为东西走向)两旁的两个村庄,A村到公路l的距离AC=1 km,B村到公路l的距离BD=2 km,B村在A村的南偏东45°方向上.
(1)求A,B两村之间的距离;
(2)为方便村民出行,计划在公路边新建一个公共汽车站P,要求该站到两村的距离相等,请用尺规在图中作出点P的位置.(保留清晰的作图痕迹,并简要写明作法)
(四)归纳小结
1.本节课学习了哪些主要内容?
2.勾股定理,垂直平分线以及角平分线的性质与判定的应用。
3.在应用时要注意哪些问题?
随堂检测
1.如图,△ABC中,∠ACB=90°,BA的垂直平分线交CB边于D,若AB=10,AC=5,则图中等于60°的角的个数为( )
A.2 B.3 C.4 D.5
2.如图,在Rt△ABC中,∠C=90°,∠B=15°,DE是AB的中垂线,垂足为D,交BC于点E,若BE=4,则AC=________.
3.若点P是△ABC内一点,PD⊥AB于D,PE⊥BC于E,PF⊥AC于F,且PD=PE=PF,则点P是△ABC的( )
A.三条高的交点 B.三条中线的交点
C.三条角平分线的交点 D.三条中垂线的交点
4.在平面内,到A,B,C三点距离相等的点有( )
A.只有一个 B.有两个
C.有三个或三个以上 D.有一个或没有
5.如图,在四边形ABCD中,AD∥BC,E为CD的中点,连结AE,BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)FC=AD;
(2)AB=BC+AD.
6、在ΔABC中,∠C=900,∠B=300,AD是∠BAC的平分线,已知AB= ,求AD的长.
五、板书设计
把黑板分成两份,左边部分板书例题,右边部分板书学习练习题,重复使用
六、作业布置
完成课后同步练习题
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
