安庆市白泽湖中学2021-2022学年高一分班考试数学试卷(Word含答案)
文档属性
| 名称 | 安庆市白泽湖中学2021-2022学年高一分班考试数学试卷(Word含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 291.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-18 00:00:00 | ||
图片预览


文档简介
数学试卷
考试时间:120分钟 满分150分
一、选择题:本题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下列命题正确的是( )
A. 菱形可确定一个平面
B.一条直线和一个点确定一个平面
C.圆心和圆上两点可确定一个平面
D.三点确定一个平面
2.复数(为虚数单位)的共轭复数是( )
A. B. C. D.
3.已知向量,,且,则的值为( )
A. B. C. D.或
4.已知一组数据为,,,,,,,,其平均数、第百分位数和众数的大小关系是( )
A.平均数第百分位数众数 B.平均数第百分位数众数
C.第百分位数众数平均数 D.平均数第百分位数众数
5.采用分层随机抽样的方法抽取一个容量为45的样本,高二年级被抽取15人,高二年级共有300人,则这个学校共有高中学生的人数为( )
A.1350 B.900 C. 675 D.450
6.用斜二测画法画出水平放置的正方形ABCD的直观图,若直观图的面积为,则正方形ABCD的面积为( )
A. 8 B. 4 C. D.
7.在正方体中,与所成的角为( )
A. B. C. D.
8. 在△中,为边上的中线,为的中点,则( )
A. B. C. D.
9.从1,2,3,4,5,6这六个整数中任取两个数,下列各组事件中是对立事件的是( )
①恰有一个是偶数和恰有一个是奇数;②两个都是偶数和两个都是奇数;
③至少有一个是奇数和两个都是偶数;④至少有一个是奇数和至少有一个是偶数.
① B. ③ C. ②④ D. ①③
10.的内角A,B,C的对边分别为a,b,c,若的面积为,则 ( )
A. B. C. D.
11.在△ABC中,a=4,b=12,A,则此三角形( )
A.解的个数不确定 B.两解
C.一解 D.无解
12.在国庆阅兵中,某兵种A,B,C三个方阵按一定次序通过主席台,若先后次序是随机排定的,则B晚于A或C通过的概率为( )
A. B. C. D.
填空题(本大题共4小题,每小题5分,共20分)
的内角 的对边分别为 .已知,,,则角__________.
14.已知一组数据4.7,4.8,5.1,5.4,5.5,则该组数据的方差是__________.
平面向量与的夹角为,,,则 .
一个袋子中有2个红球,4个绿球,采用不放回方式从中依次随机地取出2个球,则两次取到的球颜色相同的概率为______.
解答题(本大题共70分)
(本小题满分10分)设复数
(1)求及;
(2)求.
18.(本小题满分12分)已知向量与的夹角,且,.
(1)求,;
(2)求与的夹角的余弦值.
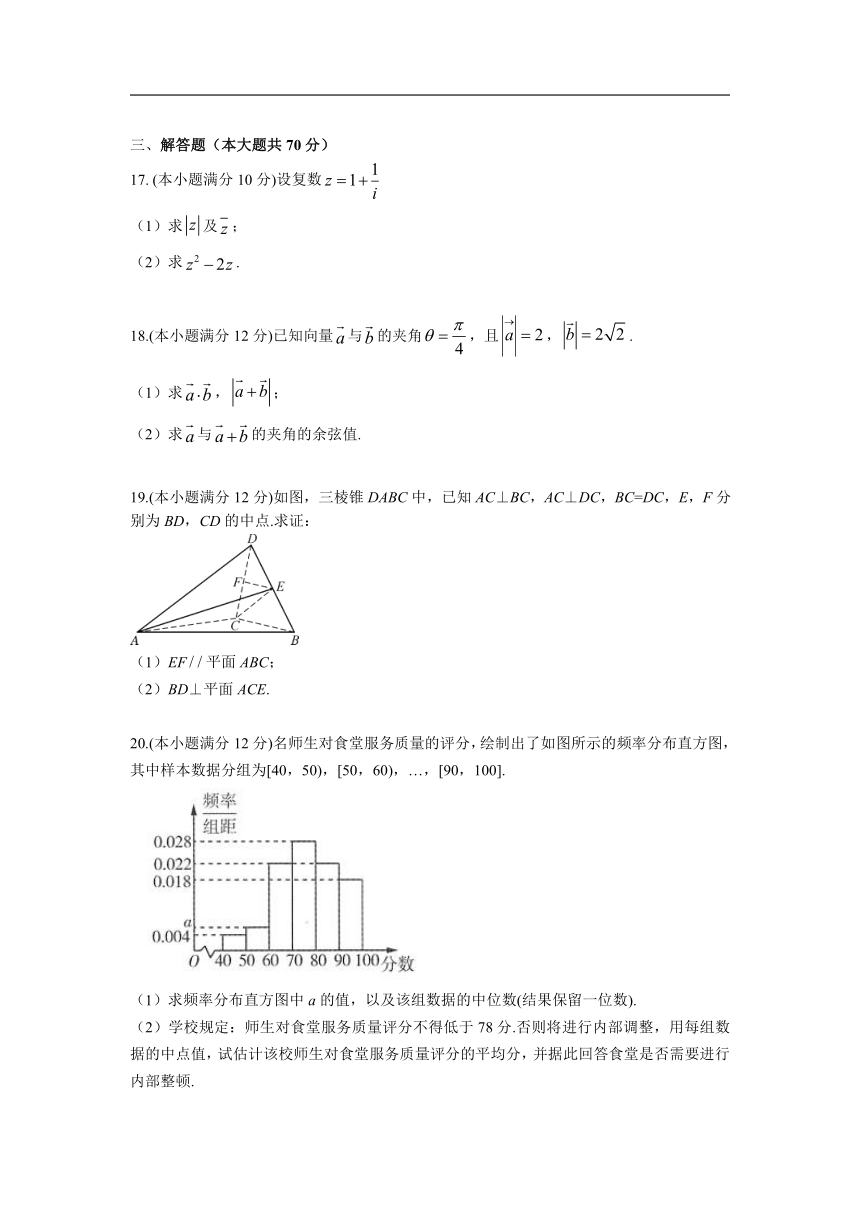
19.(本小题满分12分)如图,三棱锥DABC中,已知AC⊥BC,AC⊥DC,BC=DC,E,F分别为BD,CD的中点.求证:
(1)EF平面ABC;
(2)BD⊥平面ACE.
20.(本小题满分12分)名师生对食堂服务质量的评分,绘制出了如图所示的频率分布直方图,其中样本数据分组为[40,50),[50,60),…,[90,100].
(1)求频率分布直方图中a的值,以及该组数据的中位数(结果保留一位数).
(2)学校规定:师生对食堂服务质量评分不得低于78分.否则将进行内部调整,用每组数据的中点值,试估计该校师生对食堂服务质量评分的平均分,并据此回答食堂是否需要进行内部整顿.
(本小题满分12分).已知外接圆的半径为,角的对边长分别为.若.(1)求角C的大小.(2)若,求的值.
22.(本小题满分12分)为了深入贯彻落实习近平总书记关于疫情防控的重要指示要求,某校组织开展“战役有我,青春同行”防控疫情知识竞赛活动,某经过层层筛选后剩下甲、乙两名同学争夺一个参赛名额,该班设计了一个游戏方案决定谁去参加,规则如下:一个袋中装有6个大小相同的小球,其中标号为i的球有i个(i=1,2,3),甲、乙两名同学需从6个球中随机摸取3个球,所取球的标号之和多者获胜.
(Ⅰ)求甲所取球的标号之和为7的概率;
(Ⅱ)求甲获胜的概率.
数学答案
一、选择题
1 2 3 4 5 6 7 8 9 10 11 12
A B C D B A B C B C D D
二、填空题
13. 14. 15. 16.
三 解答题(本大题共6小题,共70分,解答应写出文字说明 证明过程或演算步骤)
17.(本小题满分10分)
(1)由题意
(2).
18.(本小题满分12分)
(1)由已知,得,
(2)设与的夹角为,
则
因此,与的夹角的余弦值为
19.(本小题满分12分)
解:(1)三棱锥中,
为的中点,为的中点,,
平面平面,
//平面.
(2),
平面,
平面,
为的中点,,
平面.
20.(本小题满分12分)
(1)由,
解得.
设该组数据的中位数为,
则,
解得,所以该组数据的中位数为.
(2)由题中数据可得对食堂服务质量评分的平均分为
,
因为76.2<78,所以食堂需要内部整顿.
21.(1);(2).
22.解:(Ⅰ)假设标号为1的球为a,标号为2的球为b,c,标号为3的球为d,e,f,
则每位同学取球标号之和的所有情况为:
abc,abd,abe,abf,acd,ace,acf,ade,adf,aef,bcd,bce,,bde,bdf,bef,cde,cdf,cef,def共20种,
甲所取球的标号之和为7的情况为:ade,adf,aef,bcd,bce,bcf共6种,
所以甲所取球的标号之和为7的概率.
(Ⅱ)由(Ⅰ)知,每人标号之和为5的概率,
标号之和为6的概率,标号之和为8的概率,标号之和为9的概率为,
则甲获胜的概率
考试时间:120分钟 满分150分
一、选择题:本题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下列命题正确的是( )
A. 菱形可确定一个平面
B.一条直线和一个点确定一个平面
C.圆心和圆上两点可确定一个平面
D.三点确定一个平面
2.复数(为虚数单位)的共轭复数是( )
A. B. C. D.
3.已知向量,,且,则的值为( )
A. B. C. D.或
4.已知一组数据为,,,,,,,,其平均数、第百分位数和众数的大小关系是( )
A.平均数第百分位数众数 B.平均数第百分位数众数
C.第百分位数众数平均数 D.平均数第百分位数众数
5.采用分层随机抽样的方法抽取一个容量为45的样本,高二年级被抽取15人,高二年级共有300人,则这个学校共有高中学生的人数为( )
A.1350 B.900 C. 675 D.450
6.用斜二测画法画出水平放置的正方形ABCD的直观图,若直观图的面积为,则正方形ABCD的面积为( )
A. 8 B. 4 C. D.
7.在正方体中,与所成的角为( )
A. B. C. D.
8. 在△中,为边上的中线,为的中点,则( )
A. B. C. D.
9.从1,2,3,4,5,6这六个整数中任取两个数,下列各组事件中是对立事件的是( )
①恰有一个是偶数和恰有一个是奇数;②两个都是偶数和两个都是奇数;
③至少有一个是奇数和两个都是偶数;④至少有一个是奇数和至少有一个是偶数.
① B. ③ C. ②④ D. ①③
10.的内角A,B,C的对边分别为a,b,c,若的面积为,则 ( )
A. B. C. D.
11.在△ABC中,a=4,b=12,A,则此三角形( )
A.解的个数不确定 B.两解
C.一解 D.无解
12.在国庆阅兵中,某兵种A,B,C三个方阵按一定次序通过主席台,若先后次序是随机排定的,则B晚于A或C通过的概率为( )
A. B. C. D.
填空题(本大题共4小题,每小题5分,共20分)
的内角 的对边分别为 .已知,,,则角__________.
14.已知一组数据4.7,4.8,5.1,5.4,5.5,则该组数据的方差是__________.
平面向量与的夹角为,,,则 .
一个袋子中有2个红球,4个绿球,采用不放回方式从中依次随机地取出2个球,则两次取到的球颜色相同的概率为______.
解答题(本大题共70分)
(本小题满分10分)设复数
(1)求及;
(2)求.
18.(本小题满分12分)已知向量与的夹角,且,.
(1)求,;
(2)求与的夹角的余弦值.
19.(本小题满分12分)如图,三棱锥DABC中,已知AC⊥BC,AC⊥DC,BC=DC,E,F分别为BD,CD的中点.求证:
(1)EF平面ABC;
(2)BD⊥平面ACE.
20.(本小题满分12分)名师生对食堂服务质量的评分,绘制出了如图所示的频率分布直方图,其中样本数据分组为[40,50),[50,60),…,[90,100].
(1)求频率分布直方图中a的值,以及该组数据的中位数(结果保留一位数).
(2)学校规定:师生对食堂服务质量评分不得低于78分.否则将进行内部调整,用每组数据的中点值,试估计该校师生对食堂服务质量评分的平均分,并据此回答食堂是否需要进行内部整顿.
(本小题满分12分).已知外接圆的半径为,角的对边长分别为.若.(1)求角C的大小.(2)若,求的值.
22.(本小题满分12分)为了深入贯彻落实习近平总书记关于疫情防控的重要指示要求,某校组织开展“战役有我,青春同行”防控疫情知识竞赛活动,某经过层层筛选后剩下甲、乙两名同学争夺一个参赛名额,该班设计了一个游戏方案决定谁去参加,规则如下:一个袋中装有6个大小相同的小球,其中标号为i的球有i个(i=1,2,3),甲、乙两名同学需从6个球中随机摸取3个球,所取球的标号之和多者获胜.
(Ⅰ)求甲所取球的标号之和为7的概率;
(Ⅱ)求甲获胜的概率.
数学答案
一、选择题
1 2 3 4 5 6 7 8 9 10 11 12
A B C D B A B C B C D D
二、填空题
13. 14. 15. 16.
三 解答题(本大题共6小题,共70分,解答应写出文字说明 证明过程或演算步骤)
17.(本小题满分10分)
(1)由题意
(2).
18.(本小题满分12分)
(1)由已知,得,
(2)设与的夹角为,
则
因此,与的夹角的余弦值为
19.(本小题满分12分)
解:(1)三棱锥中,
为的中点,为的中点,,
平面平面,
//平面.
(2),
平面,
平面,
为的中点,,
平面.
20.(本小题满分12分)
(1)由,
解得.
设该组数据的中位数为,
则,
解得,所以该组数据的中位数为.
(2)由题中数据可得对食堂服务质量评分的平均分为
,
因为76.2<78,所以食堂需要内部整顿.
21.(1);(2).
22.解:(Ⅰ)假设标号为1的球为a,标号为2的球为b,c,标号为3的球为d,e,f,
则每位同学取球标号之和的所有情况为:
abc,abd,abe,abf,acd,ace,acf,ade,adf,aef,bcd,bce,,bde,bdf,bef,cde,cdf,cef,def共20种,
甲所取球的标号之和为7的情况为:ade,adf,aef,bcd,bce,bcf共6种,
所以甲所取球的标号之和为7的概率.
(Ⅱ)由(Ⅰ)知,每人标号之和为5的概率,
标号之和为6的概率,标号之和为8的概率,标号之和为9的概率为,
则甲获胜的概率
同课章节目录
