人教版数学八年级下册 18.1.2 平行四边形的判定(第1课时)教案 (表格式)
文档属性
| 名称 | 人教版数学八年级下册 18.1.2 平行四边形的判定(第1课时)教案 (表格式) |

|
|
| 格式 | doc | ||
| 文件大小 | 81.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-19 00:00:00 | ||
图片预览


文档简介
备课人 学科 数学 备课时间 课时安排 一课时
课题 18.1.2平行四边形的判定第1课时
教学目标 知识目标掌握用一组对边平行且相等来判定平行四边形的方法.能力目标会综合运用平行四边形的四种判定方法和性质来证明问题情感、态度、价值观目标在探究讨论中养成与他人合作交流的习惯;在性质应用过程中培养独立思考的习惯;在数学活动中获得成功的体验,提高克服困难的勇气和信心。
教学重难点 学习重点:平行四边形各种判定方法及其应用,尤其是根据不同条件能正确地选择判定方法.学习难点:平行四边形的判定定理与性质定理的综合应用.
教学方法 讲练结合;讨论探究法。
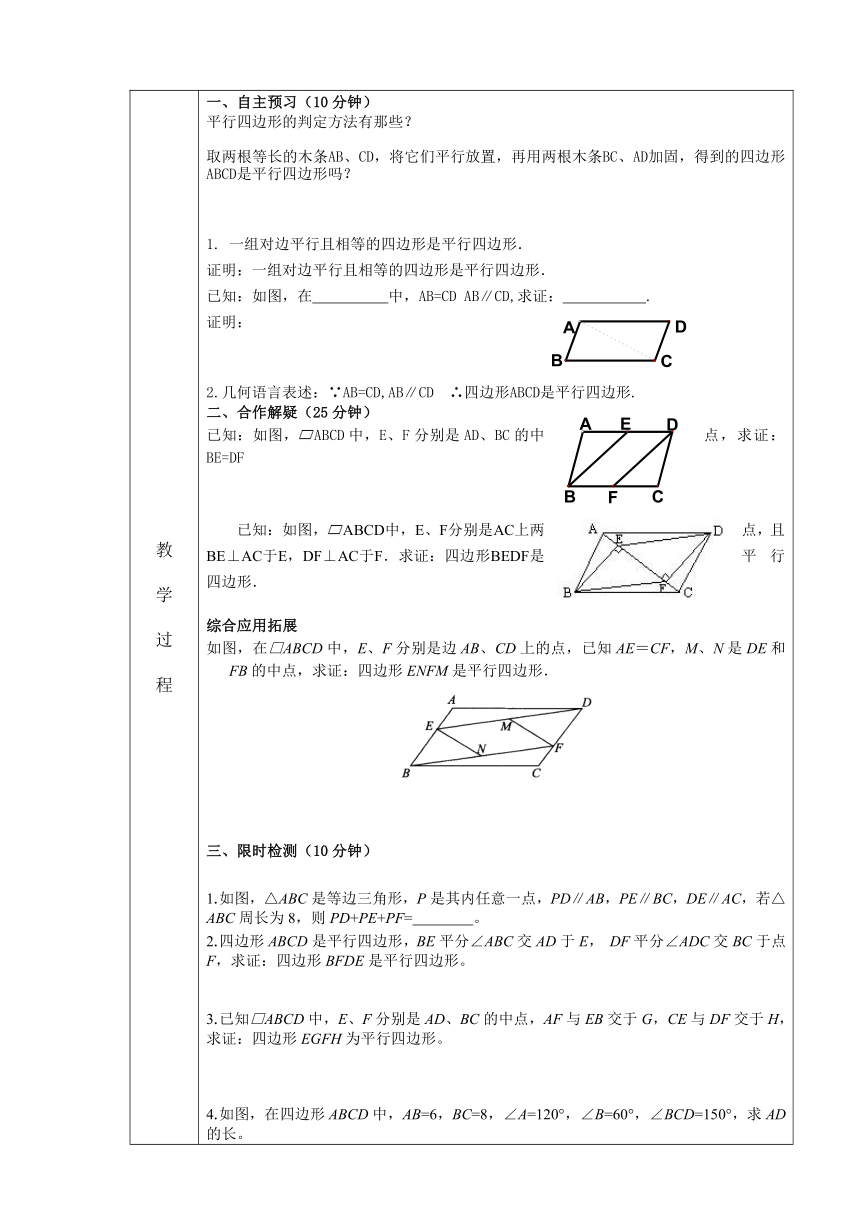
教 学 过 程 一、自主预习(10分钟)平行四边形的判定方法有那些?取两根等长的木条AB、CD,将它们平行放置,再用两根木条BC、AD加固,得到的四边形ABCD是平行四边形吗?1. 一组对边平行且相等的四边形是平行四边形.证明:一组对边平行且相等的四边形是平行四边形.已知:如图,在 中,AB=CD AB∥CD,求证: . 证明:2.几何语言表述:∵AB=CD,AB∥CD ∴四边形ABCD是平行四边形.二、合作解疑(25分钟)已知:如图,ABCD中,E、F分别是AD、BC的中点,求证:BE=DF已知:如图,ABCD中,E、F分别是AC上两点,且BE⊥AC于E,DF⊥AC于F.求证:四边形BEDF是平行四边形.综合应用拓展如图,在□ABCD中,E、F分别是边AB、CD上的点,已知AE=CF,M、N是DE和FB的中点,求证:四边形ENFM是平行四边形.三、限时检测(10分钟)1.如图,△ABC是等边三角形,P是其内任意一点,PD∥AB,PE∥BC,DE∥AC,若△ABC周长为8,则PD+PE+PF= 。2.四边形ABCD是平行四边形,BE平分∠ABC交AD于E, DF平分∠ADC交BC于点F,求证:四边形BFDE是平行四边形。3.已知□ABCD中,E、F分别是AD、BC的中点,AF与EB交于G,CE与DF交于H,求证:四边形EGFH为平行四边形。4.如图,在四边形ABCD中,AB=6,BC=8,∠A=120°,∠B=60°,∠BCD=150°,求AD的长。课 后 作 业6.能判定一个四边形是平行四边形的条件是( ).(A)一组对边平行,另一组对边相等 (B)一组对边平行,一组对角互补(C)一组对角相等,一组邻角互补 (D)一组对角相等,另一组对角互补7.能判定四边形ABCD是平行四边形的题设是( ).(A)AD=BC,AB∥CD (B)∠A=∠B,∠C=∠D(C)AB=BC,AD=DC (D)AB∥CD,CD=AB8.能判定四边形ABCD是平行四边形的条件是:∠A∶∠B∶∠C∶∠D的值为( ).(A)1∶2∶3∶4 (B)1∶4∶2∶3(C)1∶2∶2∶1 (D)1∶2∶1∶29.如图,E、F分别是□ABCD的边AB、CD的中点,则图中平行四边形的个数共有( ).(A)2个 (B)3个(C)4个 (D)5个10.□ABCD的对角线的交点在坐标原点,且AD平行于x轴,若A点坐标为(-1,2),则C点的坐标为( ).(A)(1,-2) (B)(2,-1) (C)(1,-3) (D)(2,-3)11.如图,□ABCD中,对角线AC、BD交于点O,将△AOD平移至△BEC的位置,则图中与OA相等的其他线段有( ).(A)1条 (B)2条(C)3条 (D)4条综合、运用、诊断一、解答题12.已知:如图,在□ABCD中,点E、F在对角线AC上,且AE=CF.请你以F为一个端点,和图中已标明字母的某一点连成一条新线段,猜想并证明它和图中已有的某一条线段相等(只需证明一组线段相等即可).(1)连结______;(2)猜想:______=______;(3)证明:13.如图,在△ABC中,EF为△ABC的中位线,D为BC边上一点(不与B、C重合),AD与EF交于点O,连结EF、DF,要使四边形AEDF为平行四边形,需要添加条件______.(只添加一个条件)证明:如图,在□ABCD中,E、F分别是边AD、BC上的点,已知AE=CF,AF与BE相交于点G,CE与DF相交于点H,求证:四边形EGFH是平行四边形.11.如图,在□ABCD中,E、F分别在边BA、DC的延长线上,已知AE=CF,P、Q分别是DE和FB的中点,求证:四边形EQFP是平行四边形.12.如图,在□ABCD中,E、F分别在DA、BC的延长线上,已知AE=CF,FA与BE的延长线相交于点R,EC与DF的延长线相交于点S,求证:四边形RESF是平行四边形.13.已知:如图,四边形ABCD中,AB=DC,AD=BC,点E在BC上,点F在AD上,AF=CE,EF与对角线BD交于点O,求证:O是BD的中点.14.已知:如图,△ABC中,D是AC的中点,E是线段BC延长线上一点,过点A作BE的平行线与线段ED的延长线交于点F,连结AE、CF.求证:CF∥AE.
18.1.2平行四边形的判定第二课时一、自主预习二、合作解疑综合应用拓展三、限时检测如图,在□ABCD中,E、F分别是边AD、BC上的点,已知AE=CF,AF与BE相交于点G,CE与DF相交于点H,求证:四边形EGFH是平行四边形.
附:板书设计
课题 18.1.2平行四边形的判定第1课时
教学目标 知识目标掌握用一组对边平行且相等来判定平行四边形的方法.能力目标会综合运用平行四边形的四种判定方法和性质来证明问题情感、态度、价值观目标在探究讨论中养成与他人合作交流的习惯;在性质应用过程中培养独立思考的习惯;在数学活动中获得成功的体验,提高克服困难的勇气和信心。
教学重难点 学习重点:平行四边形各种判定方法及其应用,尤其是根据不同条件能正确地选择判定方法.学习难点:平行四边形的判定定理与性质定理的综合应用.
教学方法 讲练结合;讨论探究法。
教 学 过 程 一、自主预习(10分钟)平行四边形的判定方法有那些?取两根等长的木条AB、CD,将它们平行放置,再用两根木条BC、AD加固,得到的四边形ABCD是平行四边形吗?1. 一组对边平行且相等的四边形是平行四边形.证明:一组对边平行且相等的四边形是平行四边形.已知:如图,在 中,AB=CD AB∥CD,求证: . 证明:2.几何语言表述:∵AB=CD,AB∥CD ∴四边形ABCD是平行四边形.二、合作解疑(25分钟)已知:如图,ABCD中,E、F分别是AD、BC的中点,求证:BE=DF已知:如图,ABCD中,E、F分别是AC上两点,且BE⊥AC于E,DF⊥AC于F.求证:四边形BEDF是平行四边形.综合应用拓展如图,在□ABCD中,E、F分别是边AB、CD上的点,已知AE=CF,M、N是DE和FB的中点,求证:四边形ENFM是平行四边形.三、限时检测(10分钟)1.如图,△ABC是等边三角形,P是其内任意一点,PD∥AB,PE∥BC,DE∥AC,若△ABC周长为8,则PD+PE+PF= 。2.四边形ABCD是平行四边形,BE平分∠ABC交AD于E, DF平分∠ADC交BC于点F,求证:四边形BFDE是平行四边形。3.已知□ABCD中,E、F分别是AD、BC的中点,AF与EB交于G,CE与DF交于H,求证:四边形EGFH为平行四边形。4.如图,在四边形ABCD中,AB=6,BC=8,∠A=120°,∠B=60°,∠BCD=150°,求AD的长。课 后 作 业6.能判定一个四边形是平行四边形的条件是( ).(A)一组对边平行,另一组对边相等 (B)一组对边平行,一组对角互补(C)一组对角相等,一组邻角互补 (D)一组对角相等,另一组对角互补7.能判定四边形ABCD是平行四边形的题设是( ).(A)AD=BC,AB∥CD (B)∠A=∠B,∠C=∠D(C)AB=BC,AD=DC (D)AB∥CD,CD=AB8.能判定四边形ABCD是平行四边形的条件是:∠A∶∠B∶∠C∶∠D的值为( ).(A)1∶2∶3∶4 (B)1∶4∶2∶3(C)1∶2∶2∶1 (D)1∶2∶1∶29.如图,E、F分别是□ABCD的边AB、CD的中点,则图中平行四边形的个数共有( ).(A)2个 (B)3个(C)4个 (D)5个10.□ABCD的对角线的交点在坐标原点,且AD平行于x轴,若A点坐标为(-1,2),则C点的坐标为( ).(A)(1,-2) (B)(2,-1) (C)(1,-3) (D)(2,-3)11.如图,□ABCD中,对角线AC、BD交于点O,将△AOD平移至△BEC的位置,则图中与OA相等的其他线段有( ).(A)1条 (B)2条(C)3条 (D)4条综合、运用、诊断一、解答题12.已知:如图,在□ABCD中,点E、F在对角线AC上,且AE=CF.请你以F为一个端点,和图中已标明字母的某一点连成一条新线段,猜想并证明它和图中已有的某一条线段相等(只需证明一组线段相等即可).(1)连结______;(2)猜想:______=______;(3)证明:13.如图,在△ABC中,EF为△ABC的中位线,D为BC边上一点(不与B、C重合),AD与EF交于点O,连结EF、DF,要使四边形AEDF为平行四边形,需要添加条件______.(只添加一个条件)证明:如图,在□ABCD中,E、F分别是边AD、BC上的点,已知AE=CF,AF与BE相交于点G,CE与DF相交于点H,求证:四边形EGFH是平行四边形.11.如图,在□ABCD中,E、F分别在边BA、DC的延长线上,已知AE=CF,P、Q分别是DE和FB的中点,求证:四边形EQFP是平行四边形.12.如图,在□ABCD中,E、F分别在DA、BC的延长线上,已知AE=CF,FA与BE的延长线相交于点R,EC与DF的延长线相交于点S,求证:四边形RESF是平行四边形.13.已知:如图,四边形ABCD中,AB=DC,AD=BC,点E在BC上,点F在AD上,AF=CE,EF与对角线BD交于点O,求证:O是BD的中点.14.已知:如图,△ABC中,D是AC的中点,E是线段BC延长线上一点,过点A作BE的平行线与线段ED的延长线交于点F,连结AE、CF.求证:CF∥AE.
18.1.2平行四边形的判定第二课时一、自主预习二、合作解疑综合应用拓展三、限时检测如图,在□ABCD中,E、F分别是边AD、BC上的点,已知AE=CF,AF与BE相交于点G,CE与DF相交于点H,求证:四边形EGFH是平行四边形.
附:板书设计
