5.6应用一元一次方程--追赶小明 课件(共33张PPT)
文档属性
| 名称 | 5.6应用一元一次方程--追赶小明 课件(共33张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-18 00:00:00 | ||
图片预览











文档简介
(共33张PPT)
5.6应用一元一次方程--追赶小明
第五章
一元一次方程
2021-2022学年七年级数学上册同步(北师版)
学习目标
1.通过学习列方程解决实际问题,进一步感知数学在生活中的作用。
2.通过分析追及问题中的数量关系,从而建立方程解决实际问题.进一步发展分析问题,解决问题的能力。
导入新课
龟兔赛跑
导入新课
①我坐车以40公里/小时的速度从家出发到学校需要3小时,那么我家到学校有_____公里。
②如果我想用2小时的时间从家出发到学校,那么我需要的速度为____公里/小时。
③如果我以80公里每小时的速度从家出发到学校,那么需要用______小时。
路程=速度×时间
60
1.5
120
速度=路程÷时间
时间=路程÷速度
讲授新课
追及问题
小明每天早上要在7: 50之前赶到距家1 000 m的学校上学.一天,小明以80 m/min的速度出发,5 min后,小明的爸爸发现他忘了带语文书.于是,爸爸立即以180 m/min的速度去追小明,并且在途中追上了他.
(1)爸爸追上小明用了多长时间?
(2)追上小明时,距离学校还有多远?
讲授新课
分析
家
学校
80m/min
小明走的路程=爸爸走的路程
等量关系:
5min
180m/min
怎么求爸爸追上小明的时间?
小明走的总时间-爸爸追的时间=5 min
讲授新课
1.用简单的“线段图”表示演示的追赶过程.
80×5
80x
180x
2.路程、速度和时间三者之间有何关系呢?“线段图”反映了怎样的等量关系?
家
学校
讲授新课
解得 x = 4
(1)设爸爸追上小明用了x min
80×5+80x = 180x
因此,爸爸追上小明用了4min。
解:
小明:
爸爸:
80×5
80x
180x
根据题意得:
讲授新课
(2)追上小明时,距离学校还有多远?
180×4
1000 m
?
解:
180×4=720(m)
1000-720=280(m)
所以,追上小明时,距离学校还有280 m。
(1)对于同向同时不同地的问题,如图所示,甲的行程-乙的行程=两出发地的距离;
甲、乙两人同向出发,甲追乙这类问题为追及问题:
对于行程问题,通常借助“线段图”来分析问题中的数量关系.
归纳总结
讲授新课
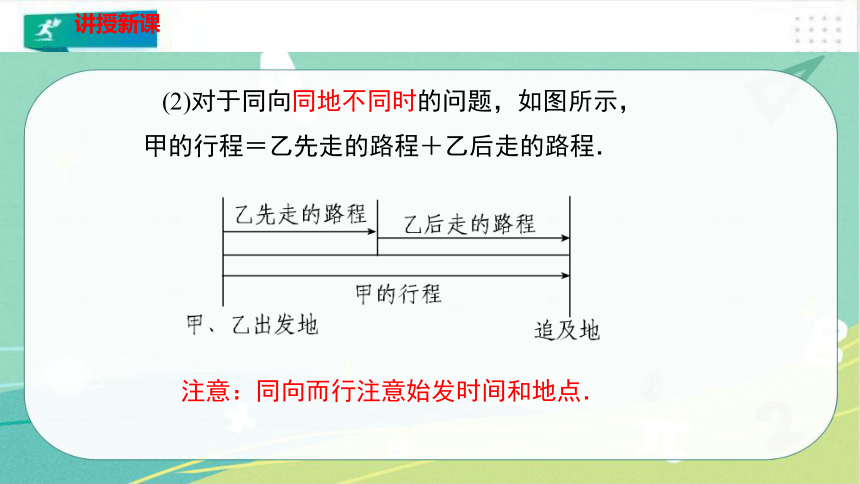
(2)对于同向同地不同时的问题,如图所示,甲的行程=乙先走的路程+乙后走的路程.
注意:同向而行注意始发时间和地点.
讲授新课
1.追及问题中的等量关系:
①快者走的路程-慢者走的路程=追及路程;
②若同时出发,快者追上慢者时,快者用的时间=慢者用的时间
行程问题中的等量关系:
讲授新课
相遇问题
甲、乙两人从相距180千米的A,B两地同时出发,甲骑自行车,乙骑摩托车,沿同一条路线相向匀速行驶.已知甲的速度为15千米/时,乙的速度为45千米/时,经过多少时间两人相遇?
讲授新课
分析
等量关系:
180千米
A
B
甲
乙
15千米/时
45千米/时
甲的行程+乙的行程=A、B两地间的距离
同时出发
甲行的时间=乙行的时间
经过多少时间两人相遇?
讲授新课
解:设经过 x 小时后甲、乙两人相遇。
由题意:15x+45x=180
解得x=3
答:经过3小时后两人相遇。
两人从两地出发相向而行的行程问题称为相遇问题.
往往根据路程之和等于总路程列方程.如图所示,甲的行程+乙的行程=两地距离.
归纳总结
讲授新课
例.小明和他的哥哥早晨起来沿长为400 m的环形跑道练习跑步.小明跑2圈用的时间和他的哥哥跑3圈用的时间相等.两人同时同地同向出发,结果经过2 min 40 s他们第一次相遇,若他们两人同时同地反向出发,则经过几秒他们第一次相遇?
讲授新课
解:设小明的速度为x m/s,
则他的哥哥的速度为 x m/s,
由题意得160x=160× -400.
解得x=5.
则小明的哥哥的速度为5× =7.5(m/s).
设经过y s他们第一次相遇,
由题意,得(5+7.5)y=400.解得y=32.
答:经过32s他们第一次相遇.
讲授新课
环形跑道问题:设v甲>v乙,环形跑道长s米,经过t秒甲、乙第一次相遇.
一般有如下两种情形:
总结
①同时同地、同向而行:
v甲t-v乙t=s.
①同时同地、背向而行:
v甲t+v乙t=s.
讲授新课
行程问题中的等量关系:
2.相遇问题中的等量关系:
①甲走的路程+乙走的路程=甲、乙出发点之间的路程;
②若甲、乙同时出发,甲用的时间=乙用的时间.
讲授新课
航行问题
一艘轮船在A、B两地之间航行,顺流用3h,逆流航行比顺流航行多用30min,轮船在静水中的速度为26km/h,求水流的速度。
讲授新课
顺水中的航速=静水中的航速 + 水流速度
顺水中
逆水中
3h
分析
等量关系:
3.5h
逆水中的航速=静水中的航速-水流速度
26km/h
顺水中的航程=逆水中的航程
设水流速度为x千米/小时
解:
3(x+26)=3.5(26-x)
解得:x=2
答:水流速度为2千米/小时
讲授新课
当堂检测
问题1:后队追上前队用了多长时间?
1.育红学校七年级学生步行到郊外旅行.七(1)班的学生组成前队,步行的速度为4千米/小时,七(2)班的学生组成后队,速度为6千米/小时.前队出发1小时后,后队才出发,同时后队派一名联络员骑自行车在两队之间不间断地来回进行联络,他骑车的速度为12千米/小时.
解:设后队追上前队用了x小时,由题意
列方程得: .
6x=4x+4
解方程得:x=2.
答:后队追上前队时用了2小时.
当堂检测
问题2:后队追上前队时联络员行了多少路程?
解:由问题1得后队追上前队用了2小时,因此联络员共行进了
12 × 2 = 24 (千米)
答:后队追上前队时联络员行了24千米.
问题3:联络员第一次追上前队时用了多长时间?
解:设联络员第一次追上前队时用了x小时,由题意列方程得:
12x = 4x + 4.
解方程得:x =0.5.
答:联络员第一次追上前队时用了0.5小时.
当堂检测
问题4:当后队追上前队时,他们已经行进了多少路程?
解:设当后队追上前队时,他们已经行进了x千米,由题意列方程得:
解得:x =12
答:当后队追上前队时,他们已经行进12千米.
问题5:联络员在前队出发多少时间后第一次追上前队?
解:设联络员在前队出发x小时后第一次追上前队,
由题意列方程得:
4x = 12(x - 1)
解方程得:x = 1.5
答:联络员在前队出发后1.5小时后第一次追上前队.
+1=
当堂检测
一队学生去校外进行军事训练,他们以每小时5千米的速度行进,走了18分钟,学校要将一个紧急通知传给队长,通讯员从学校出发,骑自行车以每小时14千米的速度按原路追上去,通讯员需要多长时间可以追上学生队伍?
解:设需要x小时可以追上,则可以列方程:
解方程,得
解得
即需要小时可以追上.
5×(+x)=14 x
9x=
x=
当堂检测
2.两列火车同时从相距600千米地甲乙两地相向而行, 经过4小时后两列火车在途中相遇,已知客车每小时行80千米, 货车每小时行多少千米
解: 设货车的速度为x千米/小时,根据题意可列出方程:
80×4+x×4=600,
解得: x=70 .
货车每小时行70千米.
答:
当堂检测
解:72 km/h=20 m/s,设听到回声时,汽车离山谷x m.
3.汽车以72 km/h的速度在公路上行驶,开向寂静的山谷,驾驶员摁一下喇叭,4s后听到回声,已知空气中声音的传播速度约为340 m/s,这时汽车离山谷多远?
由题意,得2x+4×20=340×4,
解得x=640.
答:听到回声时,汽车离山谷640 m.
当堂检测
4.一个车队共有n(n为正整数)辆小轿车,正以36 km/h的速度在一条笔直的街道上匀速行驶,行驶时车与车的间隔均为5.4 m,甲停在路边等人,他发现该车队从第一辆车的车头到最后一辆车的车尾经过自己身边共用了20 s的时间,假设每辆车的车长均为4.87 m.求n的值.
解:36 km/h=10 m/s,则4.87n+5.4(n-1)=20×10,
解得n=20.
答:n的值是20.
课堂小结
应用一元一次方程
——
追赶小明
等量关系
追及问题
相遇问题
特征
特征
等量关系
相向而行
双方所走路程之和=全部路程
同向而行
同地不同时
同时不同地
追着的路程=前者先行路程+后行路程
追者的路程=两者间的距离+前者所行路程
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
5.6应用一元一次方程--追赶小明
第五章
一元一次方程
2021-2022学年七年级数学上册同步(北师版)
学习目标
1.通过学习列方程解决实际问题,进一步感知数学在生活中的作用。
2.通过分析追及问题中的数量关系,从而建立方程解决实际问题.进一步发展分析问题,解决问题的能力。
导入新课
龟兔赛跑
导入新课
①我坐车以40公里/小时的速度从家出发到学校需要3小时,那么我家到学校有_____公里。
②如果我想用2小时的时间从家出发到学校,那么我需要的速度为____公里/小时。
③如果我以80公里每小时的速度从家出发到学校,那么需要用______小时。
路程=速度×时间
60
1.5
120
速度=路程÷时间
时间=路程÷速度
讲授新课
追及问题
小明每天早上要在7: 50之前赶到距家1 000 m的学校上学.一天,小明以80 m/min的速度出发,5 min后,小明的爸爸发现他忘了带语文书.于是,爸爸立即以180 m/min的速度去追小明,并且在途中追上了他.
(1)爸爸追上小明用了多长时间?
(2)追上小明时,距离学校还有多远?
讲授新课
分析
家
学校
80m/min
小明走的路程=爸爸走的路程
等量关系:
5min
180m/min
怎么求爸爸追上小明的时间?
小明走的总时间-爸爸追的时间=5 min
讲授新课
1.用简单的“线段图”表示演示的追赶过程.
80×5
80x
180x
2.路程、速度和时间三者之间有何关系呢?“线段图”反映了怎样的等量关系?
家
学校
讲授新课
解得 x = 4
(1)设爸爸追上小明用了x min
80×5+80x = 180x
因此,爸爸追上小明用了4min。
解:
小明:
爸爸:
80×5
80x
180x
根据题意得:
讲授新课
(2)追上小明时,距离学校还有多远?
180×4
1000 m
?
解:
180×4=720(m)
1000-720=280(m)
所以,追上小明时,距离学校还有280 m。
(1)对于同向同时不同地的问题,如图所示,甲的行程-乙的行程=两出发地的距离;
甲、乙两人同向出发,甲追乙这类问题为追及问题:
对于行程问题,通常借助“线段图”来分析问题中的数量关系.
归纳总结
讲授新课
(2)对于同向同地不同时的问题,如图所示,甲的行程=乙先走的路程+乙后走的路程.
注意:同向而行注意始发时间和地点.
讲授新课
1.追及问题中的等量关系:
①快者走的路程-慢者走的路程=追及路程;
②若同时出发,快者追上慢者时,快者用的时间=慢者用的时间
行程问题中的等量关系:
讲授新课
相遇问题
甲、乙两人从相距180千米的A,B两地同时出发,甲骑自行车,乙骑摩托车,沿同一条路线相向匀速行驶.已知甲的速度为15千米/时,乙的速度为45千米/时,经过多少时间两人相遇?
讲授新课
分析
等量关系:
180千米
A
B
甲
乙
15千米/时
45千米/时
甲的行程+乙的行程=A、B两地间的距离
同时出发
甲行的时间=乙行的时间
经过多少时间两人相遇?
讲授新课
解:设经过 x 小时后甲、乙两人相遇。
由题意:15x+45x=180
解得x=3
答:经过3小时后两人相遇。
两人从两地出发相向而行的行程问题称为相遇问题.
往往根据路程之和等于总路程列方程.如图所示,甲的行程+乙的行程=两地距离.
归纳总结
讲授新课
例.小明和他的哥哥早晨起来沿长为400 m的环形跑道练习跑步.小明跑2圈用的时间和他的哥哥跑3圈用的时间相等.两人同时同地同向出发,结果经过2 min 40 s他们第一次相遇,若他们两人同时同地反向出发,则经过几秒他们第一次相遇?
讲授新课
解:设小明的速度为x m/s,
则他的哥哥的速度为 x m/s,
由题意得160x=160× -400.
解得x=5.
则小明的哥哥的速度为5× =7.5(m/s).
设经过y s他们第一次相遇,
由题意,得(5+7.5)y=400.解得y=32.
答:经过32s他们第一次相遇.
讲授新课
环形跑道问题:设v甲>v乙,环形跑道长s米,经过t秒甲、乙第一次相遇.
一般有如下两种情形:
总结
①同时同地、同向而行:
v甲t-v乙t=s.
①同时同地、背向而行:
v甲t+v乙t=s.
讲授新课
行程问题中的等量关系:
2.相遇问题中的等量关系:
①甲走的路程+乙走的路程=甲、乙出发点之间的路程;
②若甲、乙同时出发,甲用的时间=乙用的时间.
讲授新课
航行问题
一艘轮船在A、B两地之间航行,顺流用3h,逆流航行比顺流航行多用30min,轮船在静水中的速度为26km/h,求水流的速度。
讲授新课
顺水中的航速=静水中的航速 + 水流速度
顺水中
逆水中
3h
分析
等量关系:
3.5h
逆水中的航速=静水中的航速-水流速度
26km/h
顺水中的航程=逆水中的航程
设水流速度为x千米/小时
解:
3(x+26)=3.5(26-x)
解得:x=2
答:水流速度为2千米/小时
讲授新课
当堂检测
问题1:后队追上前队用了多长时间?
1.育红学校七年级学生步行到郊外旅行.七(1)班的学生组成前队,步行的速度为4千米/小时,七(2)班的学生组成后队,速度为6千米/小时.前队出发1小时后,后队才出发,同时后队派一名联络员骑自行车在两队之间不间断地来回进行联络,他骑车的速度为12千米/小时.
解:设后队追上前队用了x小时,由题意
列方程得: .
6x=4x+4
解方程得:x=2.
答:后队追上前队时用了2小时.
当堂检测
问题2:后队追上前队时联络员行了多少路程?
解:由问题1得后队追上前队用了2小时,因此联络员共行进了
12 × 2 = 24 (千米)
答:后队追上前队时联络员行了24千米.
问题3:联络员第一次追上前队时用了多长时间?
解:设联络员第一次追上前队时用了x小时,由题意列方程得:
12x = 4x + 4.
解方程得:x =0.5.
答:联络员第一次追上前队时用了0.5小时.
当堂检测
问题4:当后队追上前队时,他们已经行进了多少路程?
解:设当后队追上前队时,他们已经行进了x千米,由题意列方程得:
解得:x =12
答:当后队追上前队时,他们已经行进12千米.
问题5:联络员在前队出发多少时间后第一次追上前队?
解:设联络员在前队出发x小时后第一次追上前队,
由题意列方程得:
4x = 12(x - 1)
解方程得:x = 1.5
答:联络员在前队出发后1.5小时后第一次追上前队.
+1=
当堂检测
一队学生去校外进行军事训练,他们以每小时5千米的速度行进,走了18分钟,学校要将一个紧急通知传给队长,通讯员从学校出发,骑自行车以每小时14千米的速度按原路追上去,通讯员需要多长时间可以追上学生队伍?
解:设需要x小时可以追上,则可以列方程:
解方程,得
解得
即需要小时可以追上.
5×(+x)=14 x
9x=
x=
当堂检测
2.两列火车同时从相距600千米地甲乙两地相向而行, 经过4小时后两列火车在途中相遇,已知客车每小时行80千米, 货车每小时行多少千米
解: 设货车的速度为x千米/小时,根据题意可列出方程:
80×4+x×4=600,
解得: x=70 .
货车每小时行70千米.
答:
当堂检测
解:72 km/h=20 m/s,设听到回声时,汽车离山谷x m.
3.汽车以72 km/h的速度在公路上行驶,开向寂静的山谷,驾驶员摁一下喇叭,4s后听到回声,已知空气中声音的传播速度约为340 m/s,这时汽车离山谷多远?
由题意,得2x+4×20=340×4,
解得x=640.
答:听到回声时,汽车离山谷640 m.
当堂检测
4.一个车队共有n(n为正整数)辆小轿车,正以36 km/h的速度在一条笔直的街道上匀速行驶,行驶时车与车的间隔均为5.4 m,甲停在路边等人,他发现该车队从第一辆车的车头到最后一辆车的车尾经过自己身边共用了20 s的时间,假设每辆车的车长均为4.87 m.求n的值.
解:36 km/h=10 m/s,则4.87n+5.4(n-1)=20×10,
解得n=20.
答:n的值是20.
课堂小结
应用一元一次方程
——
追赶小明
等量关系
追及问题
相遇问题
特征
特征
等量关系
相向而行
双方所走路程之和=全部路程
同向而行
同地不同时
同时不同地
追着的路程=前者先行路程+后行路程
追者的路程=两者间的距离+前者所行路程
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
