2021-2022学年青岛版八年级数学上册 1.2全等三角形的判定4课件(共52张PPT)
文档属性
| 名称 | 2021-2022学年青岛版八年级数学上册 1.2全等三角形的判定4课件(共52张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 868.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-19 00:00:00 | ||
图片预览




文档简介
(共52张PPT)
复习提问
证明一般两个三角形全等有哪些方法
1.在两个三角形中,如果有三条边对应相等,那么这两个三角形全等(简记S.S.S)
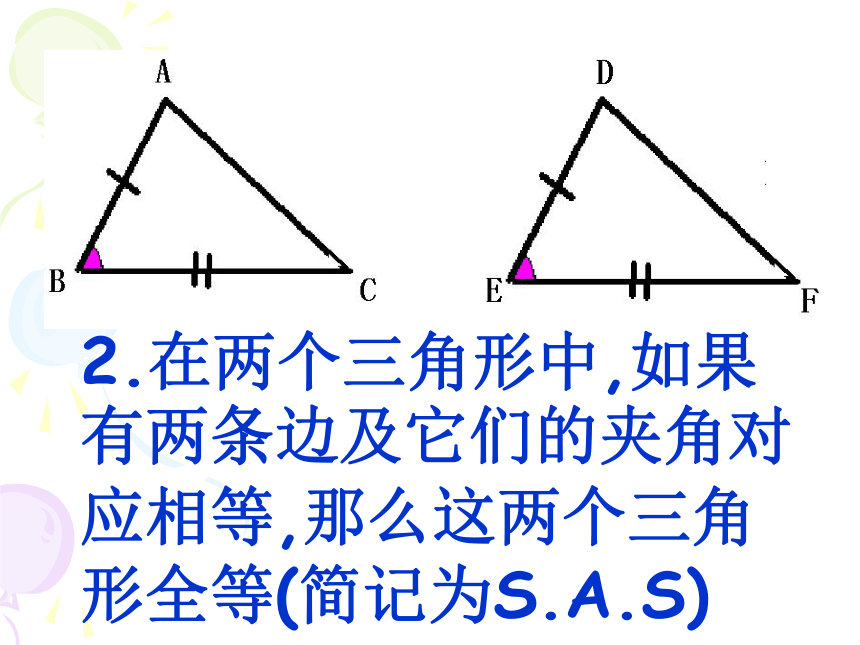
2.在两个三角形中,如果有两条边及它们的夹角对应相等,那么这两个三角形全等(简记为S.A.S)
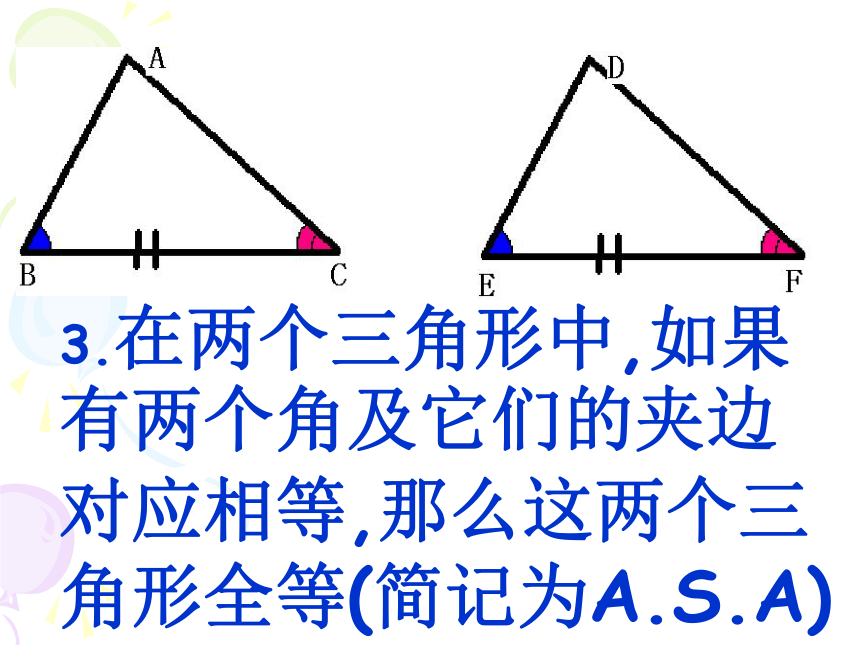
3.在两个三角形中,如果有两个角及它们的夹边对应相等,那么这两个三角形全等(简记为A.S.A)
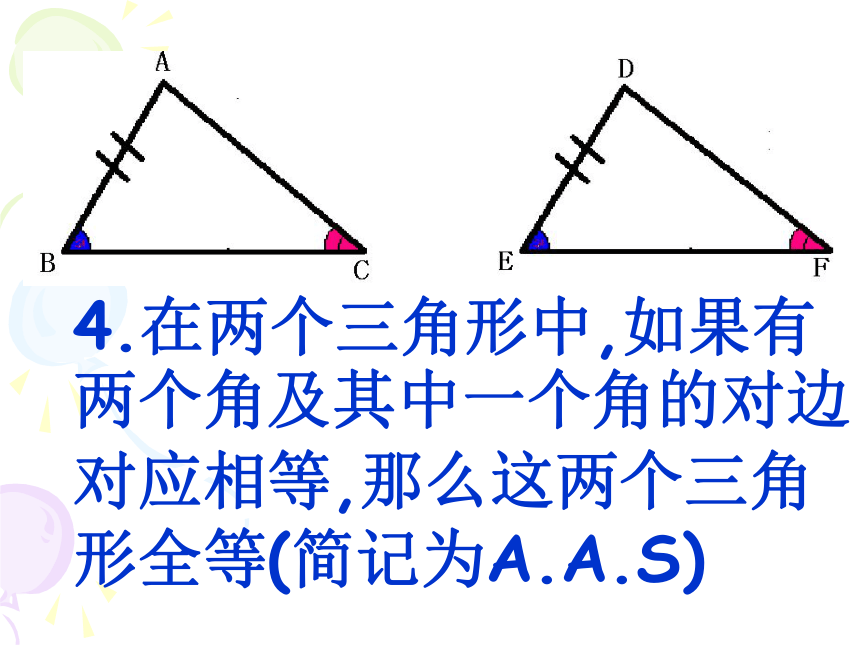
4.在两个三角形中,如果有两个角及其中一个角的对边对应相等,那么这两个三角形全等(简记为A.A.S)
A
C
B
如图, △ABC中, ∠C是直角
斜边
直角边
直角边
直角三角形用Rt△
表示。
一、判断:满足下列条件的两个三角形是否全等 为什么
1.一个锐角及这个锐角的对边对应相等的两个直角三角形.
全等
(AAS)
练一练
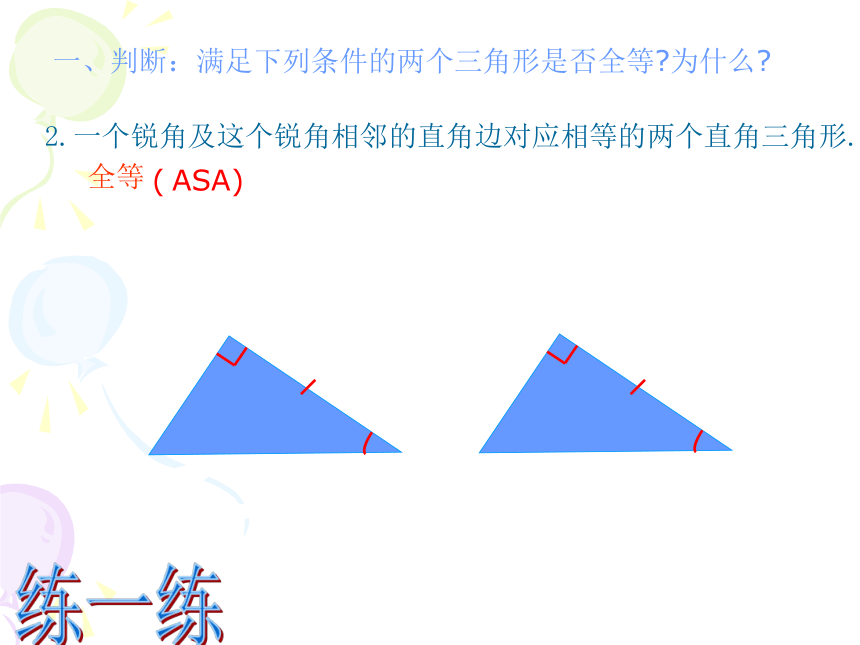
2.一个锐角及这个锐角相邻的直角边对应相等的两个直角三角形.
全等
( ASA)
一、判断:满足下列条件的两个三角形是否全等 为什么
练一练
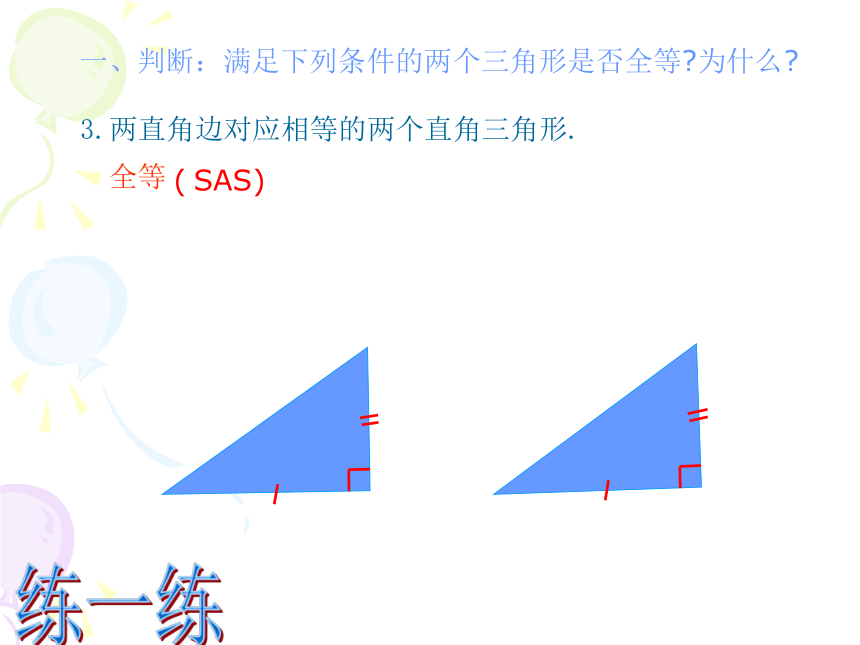
3.两直角边对应相等的两个直角三角形.
全等
( SAS)
一、判断:满足下列条件的两个三角形是否全等 为什么
练一练
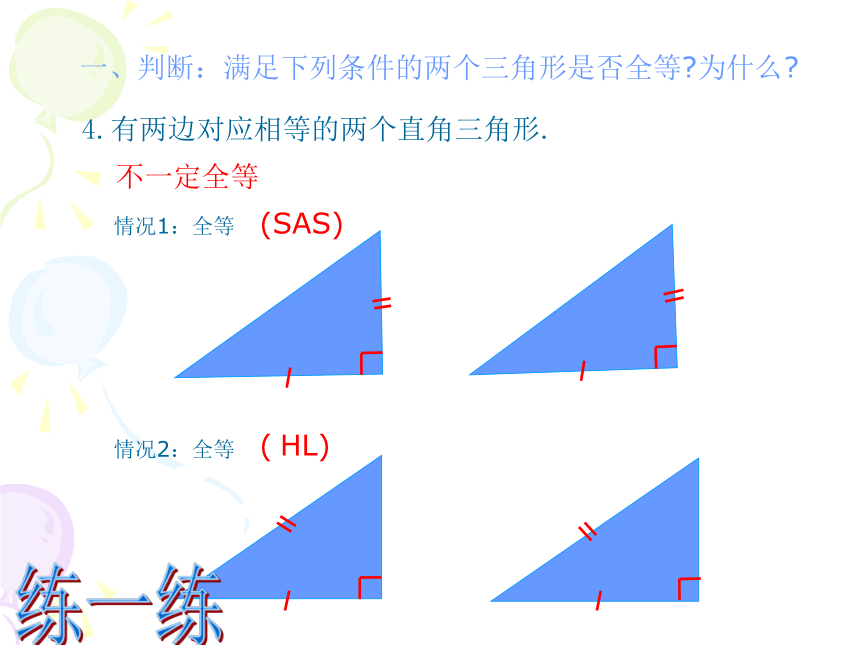
4.有两边对应相等的两个直角三角形.
不一定全等
情况1:全等
情况2:全等
(SAS)
( HL)
一、判断:满足下列条件的两个三角形是否全等 为什么
练一练
11
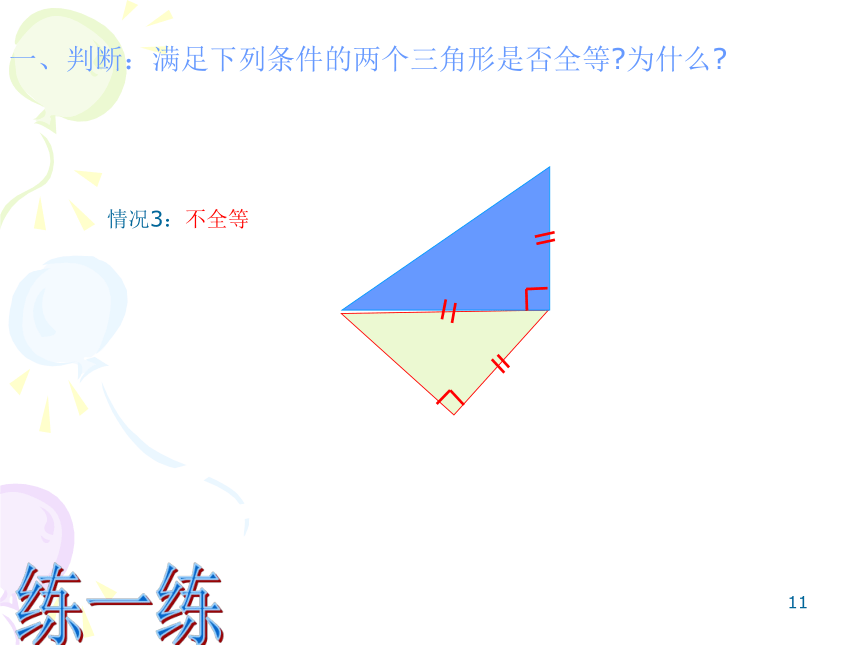
情况3:不全等
一、判断:满足下列条件的两个三角形是否全等 为什么
练一练
12
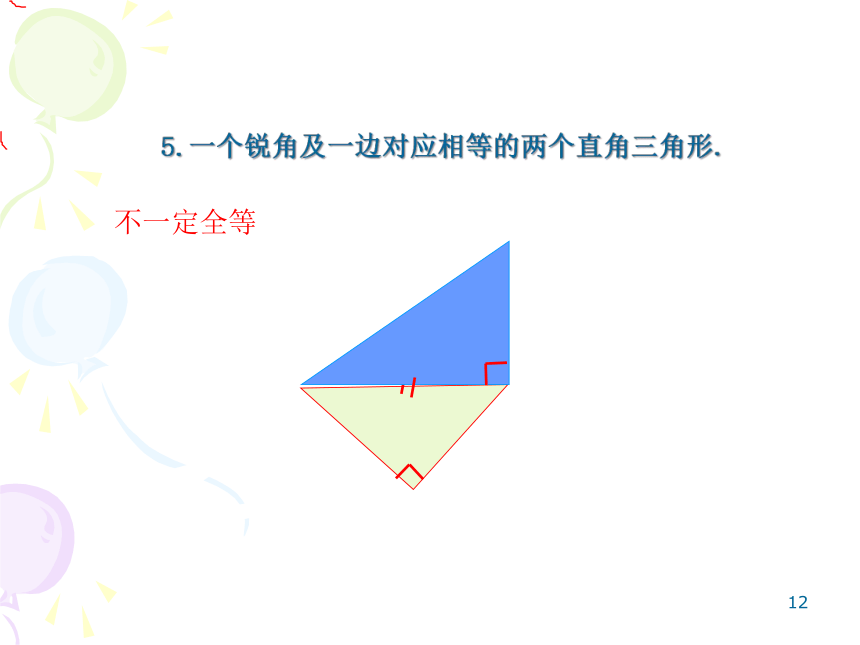
5.一个锐角及一边对应相等的两个直角三角形.
不一定全等
想一想
对于一般的三角形“S.S.A”可不可以证明三角形全等
A
B
C
D
但直角三角形作为特殊的三角形,
会不会有自身独特的判定方法呢
动动手 做一做
画一个Rt△ABC,使得∠C=90°,一直角边CA=
8cm,斜边AB=10cm.
A
B
C
10cm
10cm
10cm
10cm
10cm
8cm
8cm
8cm
8cm
8cm
动动手 做一做
1:画∠MCN=90°;
C
N
M
动动手 做一做
1:画∠MCN=90°;
C
N
M
2:在射线CM上截取CA=8cm;
A
1:画∠MCN=90°;
2:在射线CM上截取CA=8cm;
动动手 做一做
3:以A为圆心,10cm为半径画弧,交射线CN于B;
C
N
M
A
B
C
N
M
B
动动手 做一做
A
4:连结AB;
△ABC即为所要
画的三角形
1:画∠MCN=90°;
2:在射线CM上截取CA=8cm;
3:以A为圆心,10cm为半径画弧,交射线CN于B;
把我们刚画好的直角三角形剪下来,和同桌的比比看,这些直角三角形有怎样的关系呢?
你发现了什么?
A
B
C
10cm
10cm
10cm
10cm
10cm
8cm
8cm
8cm
8cm
8cm
A′
B ′
C ′
10cm
10cm
10cm
10cm
10cm
8cm
8cm
8cm
8cm
8cm
Rt△ABC≌Rt△A′B′C′
斜边、直角边公理
有斜边和一条直角边对应相等的两个直角三角形全等.
简写成“斜边、直角边”
或“HL”
前提
条件1
条件2
斜边、直角边公理 (HL)推理格式
A
B
C
A ′
B′
C ′
∴在Rt△ABC和Rt△A B C 中
AB=A B
BC=B C
∴Rt△ABC≌
∵∠C=∠C′=90°
Rt△A B C
(HL)
1.如图所示,在△ABC 和△ABD 中,AC⊥BC, AD⊥BD,
垂足分别为C、D,AD =BC,求证:△ABC ≌△BAD。
A
B
D
C
证明: ∵ AC⊥BC, BD⊥AD
∴∠C与∠D都是直角。
AB =BA
AC =BD
Rt△ABC ≌Rt△BAD (HL)。
∴ BC﹦AD
在 Rt△ABC 和 Rt△BAD 中,
如图 在△ABC中,已知BD⊥AC,CE ⊥AB,BD=CE。说明△EBC≌ △DCB的理由。
A
B
C
∟
∟
E
D
如图,AC=AD,∠C=∠D=Rt∠ ,你能说明点A在∠CBD的平分线上吗?
例2
已知:如图, △ABC是等腰三角形,AB=AC,AD是高
求证:BD=CD ;∠BAD=∠CAD
A
B
C
D
证明:∵AD是高
∴∠ADB=∠ADC=90°
在Rt△ADB和Rt△ADC中
AB=AC
AD=AD(公共边)
∴ Rt△ADB≌Rt△ADC(HL)
∴BD=CD,∠BAD=∠CAD
(全等三角形的对应边相等,对应角相等)
如图,∠B=∠E=Rt∠,AB=AE,∠1=∠2,则∠3=∠4 ,请说明理由。
2、如图,∠ABD=∠ACD=90°,∠1=∠2,则AD平分∠BAC,请说明理由。
课堂练习
练习3 如图,AB =CD,AE⊥BC,DF⊥BC,垂
足分别为E ,F,CE =BF.求证:AE =DF.
A
B
C
D
E
F
例3、如图,已知P是∠AOB内部一点,PD⊥OA, PE⊥OB,D,E分别是垂足,且PD=PE,则点P在
∠AOB的平分线上。请说明理由。
4.如图所示,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC 和∠DFE 的大小有什么关系?
∠ABC +∠DFE =90°
解:在Rt△ABC 和Rt△DEF 中
BC =EF
AC =DF
∴ Rt△ABC ≌Rt△DEF (HL)
∴∠ABC =∠DEF
(全等三角形对应角相等)
∵ ∠DEF +∠DFE =90°
∴∠ABC +∠DFE =90°
实际应用:
如图,两根长度为12米的绳子,一端系在旗杆上,另一端分别固定在地面两个木桩上,两个木桩离旗杆底部的距离相等吗?请说明你的理由。
变式1 如图,AC⊥BC,BD⊥AD,要证△ABC
≌△BAD,需要添加一个什么条件?请说明理由.
(1) ( );
(2) ( );
(3) ( );
(4) ( ).
AD = BC
AC = BD
∠DAB = ∠CBA
∠DBA = ∠CAB
HL
HL
AAS
AAS
“HL”判定方法的运用
A
B
C
D
(1) _______,∠A=∠D ( ASA )
(2) AC=DF,________ (SAS)
(3) AB=DE,BC=EF ( )
(4) AC=DF, ______ (HL)
(5) ∠A=∠D, BC=EF ( )
(6) ________,AC=DF ( AAS )
B
C
A
E
F
D
比一比
把下列说明Rt△ABC≌Rt△DEF的条件或根据补充完整.
AC=DF
BC=EF
HL
AB=DE
AAS
∠B=∠E
小结
直角三角形全等的识别
一般三角形全等的识别
S.A.S
A.S.A
A.A.S
S.S.S
S.A.S
A.S.A
A.A.S
H.L
灵活运用各种方法证明直角三角形全等
A
F
C
E
D
B
如图,AB=CD, BF⊥AC,DE⊥AC,AE=CF
求证:BF=DE
巩固练习
A
F
C
E
D
B
如图,AB=CD, BF⊥AC,DE⊥AC,AE=CF
求证:BD平分EF
G
变式训练1
如图,AB=CD, BF⊥AC,DE⊥AC,AE=CF
想想:BD平分EF吗
C
D
A
F
E
B
G
变式训练2
拓展提高
已知:如图,在△ABC和△DEF中,AP、DQ分别是高,
并且AB=DE,AP=DQ,∠BAC=∠EDF,
求证:△ABC≌△DEF
A
B
C
P
D
E
F
Q
∠BAC=∠EDF, AB=DE,∠B=∠E
分析: △ABC≌△DEF
Rt△ABP≌Rt△DEQ
AB=DE,AP=DQ
A
B
C
P
D
E
F
Q
证明:∵AP、DQ是△ABC和△DEF的高
∴∠APB=∠DQE=90°
在Rt△ABP和Rt△DEQ中
AB=DE
AP=DQ
∴Rt△ABP≌Rt△DEQ (HL)
∴ ∠B=∠E (全等三角形的对应角相等)
在△ABC和△DEF中
∠BAC=∠EDF
AB=DE
∠B=∠E (已证)
∴△ABC≌△DEF (ASA)
思维拓展
已知:如图,在△ABC和△DEF中,AP、DQ分别是高,
并且AB=DE,AP=DQ,∠BAC=∠EDF,
求证:△ABC≌△DEF
A
B
C
P
D
E
F
Q
变式1:若把∠BAC=∠EDF,改为BC=EF ,△ABC与△DEF全等吗?请说明思路。
小结
已知:如图,在△ABC和△DEF中,AP、DQ分别是高,
并且AB=DE,AP=DQ,∠BAC=∠EDF,
求证:△ABC≌△DEF
A
B
C
P
D
E
F
Q
变式1:若把∠BAC=∠EDF,改为BC=EF ,△ABC与△DEF全等吗?请说明思路。
变式2:若把∠BAC=∠EDF,改为AC=DF,△ABC与△DEF全等吗?请说明思路。
思维拓展
小结
已知:如图,在△ABC和△DEF中,AP、DQ分别是高,
并且AB=DE,AP=DQ,∠BAC=∠EDF,
求证:△ABC≌△DEF
A
B
C
P
D
E
F
Q
变式1:若把∠BAC=∠EDF,改为BC=EF ,△ABC与△DEF全等吗?请说明思路。
变式2:若把∠BAC=∠EDF,改为AC=DF,△ABC与△DEF全等吗?请说明思路。
变式3:请你把例题中的∠BAC=∠EDF改为另一个适当条件,使△ABC与△DEF仍能全等。试证明。
思维拓展
小结
A
B
C
E
D
拓展提高
46
在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于D,CE⊥DE于E.
(1)若BC在DE的同侧(如图①)且AD=CE,说明:BA⊥AC.
(2)若BC在DE的两侧(如图②)其他条件不变,问AB与AC仍垂直吗?若是请予证明,若不是请说明理由.
学以致用
如图等边△AEB与等边△BCD在线段AC的同侧。
求证: △ABD≌△EBC
A
B
C
E
D
学以致用
C
D
E
B
A
如图,△ABC与△DCE都是等边三角形,点D在BC上,AD与BE相等吗?试说明理由。
学以致用
E
D
C
B
A
如图,△ABC与△DCE都是等边三角形,点D在△ABC内,AD与BE相等吗?试说明理由。
学以致用
E
D
C
B
A
如图,△ABC与△DCE都是等边三角形,点D.E在△ABC外,AD与BE相等吗?试说明理由。
学以致用
已知如图△ABD与△ACE均为等边三角形,求证:DC=BE
B
A
C
D
E
学以致用
如图,已知正方形ABCD和等腰直角三角形△ECF,试说明BE=DF。
A
B
C
D
E
F
学以致用
复习提问
证明一般两个三角形全等有哪些方法
1.在两个三角形中,如果有三条边对应相等,那么这两个三角形全等(简记S.S.S)
2.在两个三角形中,如果有两条边及它们的夹角对应相等,那么这两个三角形全等(简记为S.A.S)
3.在两个三角形中,如果有两个角及它们的夹边对应相等,那么这两个三角形全等(简记为A.S.A)
4.在两个三角形中,如果有两个角及其中一个角的对边对应相等,那么这两个三角形全等(简记为A.A.S)
A
C
B
如图, △ABC中, ∠C是直角
斜边
直角边
直角边
直角三角形用Rt△
表示。
一、判断:满足下列条件的两个三角形是否全等 为什么
1.一个锐角及这个锐角的对边对应相等的两个直角三角形.
全等
(AAS)
练一练
2.一个锐角及这个锐角相邻的直角边对应相等的两个直角三角形.
全等
( ASA)
一、判断:满足下列条件的两个三角形是否全等 为什么
练一练
3.两直角边对应相等的两个直角三角形.
全等
( SAS)
一、判断:满足下列条件的两个三角形是否全等 为什么
练一练
4.有两边对应相等的两个直角三角形.
不一定全等
情况1:全等
情况2:全等
(SAS)
( HL)
一、判断:满足下列条件的两个三角形是否全等 为什么
练一练
11
情况3:不全等
一、判断:满足下列条件的两个三角形是否全等 为什么
练一练
12
5.一个锐角及一边对应相等的两个直角三角形.
不一定全等
想一想
对于一般的三角形“S.S.A”可不可以证明三角形全等
A
B
C
D
但直角三角形作为特殊的三角形,
会不会有自身独特的判定方法呢
动动手 做一做
画一个Rt△ABC,使得∠C=90°,一直角边CA=
8cm,斜边AB=10cm.
A
B
C
10cm
10cm
10cm
10cm
10cm
8cm
8cm
8cm
8cm
8cm
动动手 做一做
1:画∠MCN=90°;
C
N
M
动动手 做一做
1:画∠MCN=90°;
C
N
M
2:在射线CM上截取CA=8cm;
A
1:画∠MCN=90°;
2:在射线CM上截取CA=8cm;
动动手 做一做
3:以A为圆心,10cm为半径画弧,交射线CN于B;
C
N
M
A
B
C
N
M
B
动动手 做一做
A
4:连结AB;
△ABC即为所要
画的三角形
1:画∠MCN=90°;
2:在射线CM上截取CA=8cm;
3:以A为圆心,10cm为半径画弧,交射线CN于B;
把我们刚画好的直角三角形剪下来,和同桌的比比看,这些直角三角形有怎样的关系呢?
你发现了什么?
A
B
C
10cm
10cm
10cm
10cm
10cm
8cm
8cm
8cm
8cm
8cm
A′
B ′
C ′
10cm
10cm
10cm
10cm
10cm
8cm
8cm
8cm
8cm
8cm
Rt△ABC≌Rt△A′B′C′
斜边、直角边公理
有斜边和一条直角边对应相等的两个直角三角形全等.
简写成“斜边、直角边”
或“HL”
前提
条件1
条件2
斜边、直角边公理 (HL)推理格式
A
B
C
A ′
B′
C ′
∴在Rt△ABC和Rt△A B C 中
AB=A B
BC=B C
∴Rt△ABC≌
∵∠C=∠C′=90°
Rt△A B C
(HL)
1.如图所示,在△ABC 和△ABD 中,AC⊥BC, AD⊥BD,
垂足分别为C、D,AD =BC,求证:△ABC ≌△BAD。
A
B
D
C
证明: ∵ AC⊥BC, BD⊥AD
∴∠C与∠D都是直角。
AB =BA
AC =BD
Rt△ABC ≌Rt△BAD (HL)。
∴ BC﹦AD
在 Rt△ABC 和 Rt△BAD 中,
如图 在△ABC中,已知BD⊥AC,CE ⊥AB,BD=CE。说明△EBC≌ △DCB的理由。
A
B
C
∟
∟
E
D
如图,AC=AD,∠C=∠D=Rt∠ ,你能说明点A在∠CBD的平分线上吗?
例2
已知:如图, △ABC是等腰三角形,AB=AC,AD是高
求证:BD=CD ;∠BAD=∠CAD
A
B
C
D
证明:∵AD是高
∴∠ADB=∠ADC=90°
在Rt△ADB和Rt△ADC中
AB=AC
AD=AD(公共边)
∴ Rt△ADB≌Rt△ADC(HL)
∴BD=CD,∠BAD=∠CAD
(全等三角形的对应边相等,对应角相等)
如图,∠B=∠E=Rt∠,AB=AE,∠1=∠2,则∠3=∠4 ,请说明理由。
2、如图,∠ABD=∠ACD=90°,∠1=∠2,则AD平分∠BAC,请说明理由。
课堂练习
练习3 如图,AB =CD,AE⊥BC,DF⊥BC,垂
足分别为E ,F,CE =BF.求证:AE =DF.
A
B
C
D
E
F
例3、如图,已知P是∠AOB内部一点,PD⊥OA, PE⊥OB,D,E分别是垂足,且PD=PE,则点P在
∠AOB的平分线上。请说明理由。
4.如图所示,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC 和∠DFE 的大小有什么关系?
∠ABC +∠DFE =90°
解:在Rt△ABC 和Rt△DEF 中
BC =EF
AC =DF
∴ Rt△ABC ≌Rt△DEF (HL)
∴∠ABC =∠DEF
(全等三角形对应角相等)
∵ ∠DEF +∠DFE =90°
∴∠ABC +∠DFE =90°
实际应用:
如图,两根长度为12米的绳子,一端系在旗杆上,另一端分别固定在地面两个木桩上,两个木桩离旗杆底部的距离相等吗?请说明你的理由。
变式1 如图,AC⊥BC,BD⊥AD,要证△ABC
≌△BAD,需要添加一个什么条件?请说明理由.
(1) ( );
(2) ( );
(3) ( );
(4) ( ).
AD = BC
AC = BD
∠DAB = ∠CBA
∠DBA = ∠CAB
HL
HL
AAS
AAS
“HL”判定方法的运用
A
B
C
D
(1) _______,∠A=∠D ( ASA )
(2) AC=DF,________ (SAS)
(3) AB=DE,BC=EF ( )
(4) AC=DF, ______ (HL)
(5) ∠A=∠D, BC=EF ( )
(6) ________,AC=DF ( AAS )
B
C
A
E
F
D
比一比
把下列说明Rt△ABC≌Rt△DEF的条件或根据补充完整.
AC=DF
BC=EF
HL
AB=DE
AAS
∠B=∠E
小结
直角三角形全等的识别
一般三角形全等的识别
S.A.S
A.S.A
A.A.S
S.S.S
S.A.S
A.S.A
A.A.S
H.L
灵活运用各种方法证明直角三角形全等
A
F
C
E
D
B
如图,AB=CD, BF⊥AC,DE⊥AC,AE=CF
求证:BF=DE
巩固练习
A
F
C
E
D
B
如图,AB=CD, BF⊥AC,DE⊥AC,AE=CF
求证:BD平分EF
G
变式训练1
如图,AB=CD, BF⊥AC,DE⊥AC,AE=CF
想想:BD平分EF吗
C
D
A
F
E
B
G
变式训练2
拓展提高
已知:如图,在△ABC和△DEF中,AP、DQ分别是高,
并且AB=DE,AP=DQ,∠BAC=∠EDF,
求证:△ABC≌△DEF
A
B
C
P
D
E
F
Q
∠BAC=∠EDF, AB=DE,∠B=∠E
分析: △ABC≌△DEF
Rt△ABP≌Rt△DEQ
AB=DE,AP=DQ
A
B
C
P
D
E
F
Q
证明:∵AP、DQ是△ABC和△DEF的高
∴∠APB=∠DQE=90°
在Rt△ABP和Rt△DEQ中
AB=DE
AP=DQ
∴Rt△ABP≌Rt△DEQ (HL)
∴ ∠B=∠E (全等三角形的对应角相等)
在△ABC和△DEF中
∠BAC=∠EDF
AB=DE
∠B=∠E (已证)
∴△ABC≌△DEF (ASA)
思维拓展
已知:如图,在△ABC和△DEF中,AP、DQ分别是高,
并且AB=DE,AP=DQ,∠BAC=∠EDF,
求证:△ABC≌△DEF
A
B
C
P
D
E
F
Q
变式1:若把∠BAC=∠EDF,改为BC=EF ,△ABC与△DEF全等吗?请说明思路。
小结
已知:如图,在△ABC和△DEF中,AP、DQ分别是高,
并且AB=DE,AP=DQ,∠BAC=∠EDF,
求证:△ABC≌△DEF
A
B
C
P
D
E
F
Q
变式1:若把∠BAC=∠EDF,改为BC=EF ,△ABC与△DEF全等吗?请说明思路。
变式2:若把∠BAC=∠EDF,改为AC=DF,△ABC与△DEF全等吗?请说明思路。
思维拓展
小结
已知:如图,在△ABC和△DEF中,AP、DQ分别是高,
并且AB=DE,AP=DQ,∠BAC=∠EDF,
求证:△ABC≌△DEF
A
B
C
P
D
E
F
Q
变式1:若把∠BAC=∠EDF,改为BC=EF ,△ABC与△DEF全等吗?请说明思路。
变式2:若把∠BAC=∠EDF,改为AC=DF,△ABC与△DEF全等吗?请说明思路。
变式3:请你把例题中的∠BAC=∠EDF改为另一个适当条件,使△ABC与△DEF仍能全等。试证明。
思维拓展
小结
A
B
C
E
D
拓展提高
46
在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于D,CE⊥DE于E.
(1)若BC在DE的同侧(如图①)且AD=CE,说明:BA⊥AC.
(2)若BC在DE的两侧(如图②)其他条件不变,问AB与AC仍垂直吗?若是请予证明,若不是请说明理由.
学以致用
如图等边△AEB与等边△BCD在线段AC的同侧。
求证: △ABD≌△EBC
A
B
C
E
D
学以致用
C
D
E
B
A
如图,△ABC与△DCE都是等边三角形,点D在BC上,AD与BE相等吗?试说明理由。
学以致用
E
D
C
B
A
如图,△ABC与△DCE都是等边三角形,点D在△ABC内,AD与BE相等吗?试说明理由。
学以致用
E
D
C
B
A
如图,△ABC与△DCE都是等边三角形,点D.E在△ABC外,AD与BE相等吗?试说明理由。
学以致用
已知如图△ABD与△ACE均为等边三角形,求证:DC=BE
B
A
C
D
E
学以致用
如图,已知正方形ABCD和等腰直角三角形△ECF,试说明BE=DF。
A
B
C
D
E
F
学以致用
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
